信息技术教学的文化内涵探析
——以大学“离散数学”课程教学改革为例*
2014-06-21李艳玲张剑妹
李艳玲,张剑妹
(长治学院 计算机系,山西 长治 046011)
离散数学是计算机专业开设的核心基础课程,一直以来是以专业必修课的教学形式列在培养计划中。它对于计算机专业后续课程的学习以及相关科研的开展都具有非常重要的意义。由于离散数学主要研究具有离散特征的对象,这正好符合计算机的解题特点,因此计算机的普及使得离散数学找到了它应有的位置,逐步建立和发展起来。
离散数学课程主要由数理逻辑、集合论、代数结构和图论四个方面构成,通过对本课程各个教学环节的学习,重点培养学生的抽象思维能力、严谨的逻辑推理能力和自学能力,以及学生的熟练运算能力和综合运用所学知识去分析解决实际问题的能力[1]。
一、离散数学的教学现状及存在的问题
1.由于高校扩招,师范类院校的生源质量逐年降低,学生的知识水平参差不齐,学生的自觉学习能力不强。加上离散数学课程在大学二年级开设,学生刚从公共课的学习中结束,才开始接触计算机专业课程,对计算机专业的认知能力不足,不清楚开设离散数学的意义,只是感觉离散数学的理论性太强,认为它就是一门纯理论课程,学不学对将来从事计算机的应用研究并没有什么影响。
2.目前长治学院的离散数学教学已经缩减到68学时,所以教师不可能对课本中的内容进行面面俱到的讲授,而且学校没有开设上机实验内容,这对于学生理解内容抽象的概念增加了难度。
针对上述问题,我们向大同大学、忻州师范学院、太原师范学院、吕梁学院和运城学院五所本科院校发放了200多份调查问卷,在分析反馈结果的基础上,提出了如下教学理念:将孔子的教学思想和数学文化融入课堂,并结合信息技术引入开放实验,让学生了解数学问题不仅仅是抽象的概念和定理,还包括内涵丰富的数学文化和哲学文化,并把一些枯燥的操作交给计算机程序,从而激发学生的学习兴趣。
二、离散数学的哲学文化内涵探析
1.孔子的教学理念
孔子是我国历史上第一个伟大的教育家,他的教育主张和教育方法,直到今天仍然有深远的价值。教师应该善于启发诱导、循序渐进,激发学生主动学习的积极性,培养学生独立钻研的能力和综合运用所学知识分析解决问题的能力,引导他们欢快而潜心的“乐学”。孔子提倡“不愤不咎,不悱不发。举一隅不以三隅反,则不复也。”(《论语·述而》)。朱熹集注:“愤者,心求通而未得之意。悱者,口欲言而未能之貌。启,谓开其意。发,谓达其辞。物之有四隅者,举一可知其三。反者,还以相证之义。复,再告也。”意思是老师教学不能填鸭式的满堂灌,应该以学生为主体,到他苦想冥思而不得要领,郁闷苦悲着急时,再去开导启发他;如果告诉他一个角,他不能类推出另外的三个角,就不要再反复给他举例了。在教学中,学生如果能够进入这种“愤”和“悱”的状态,尽管表面看起来束手无策,但对积极的学习者来说,还隐含着拍案而起,不达目的势不罢休的趋势,这时加上教师适当、适时的“启”和“发”,学生就会茅塞顿开、悠然于心,其学习兴趣自然会被激发起来[2]。另外,如果学生不能举一反三,触类旁通,就不要再勉强教下去,教学需要掌握时机循序渐进,而不是赶进度。
2.“启发式”教学实践的应用
教学中,老师针对某一个知识点设置预习题,引导学生思考其解,让学生进入“愤”和 “悱”的状态,调动学生的积极性。比如讲解欧拉图这一知识点,先设置预习题:图1是否能一笔画出来?学生会不会做并不重要,重要的是促使学生积极思考,使其进入想解决但又不得其解的状态。在接下来的课堂教学中,就可以针对性地启发学生的思维。什么样的图可以一笔画并且能回到出发点,什么样的图可以一笔画但是不能回到出发点。最后给出欧拉图和欧拉通路的概念,达到由浅入深,由易到难,水到渠成的效果。这种方式比单纯地将现成的概念灌输给学生要好的多,后者使学生往往只知其然,不知其所以然,缺乏灵活运用和独立思考的能力。而适时地“启”和“发”旨在帮助学生弄懂事物的本质,往往会收到事半功倍的成效。
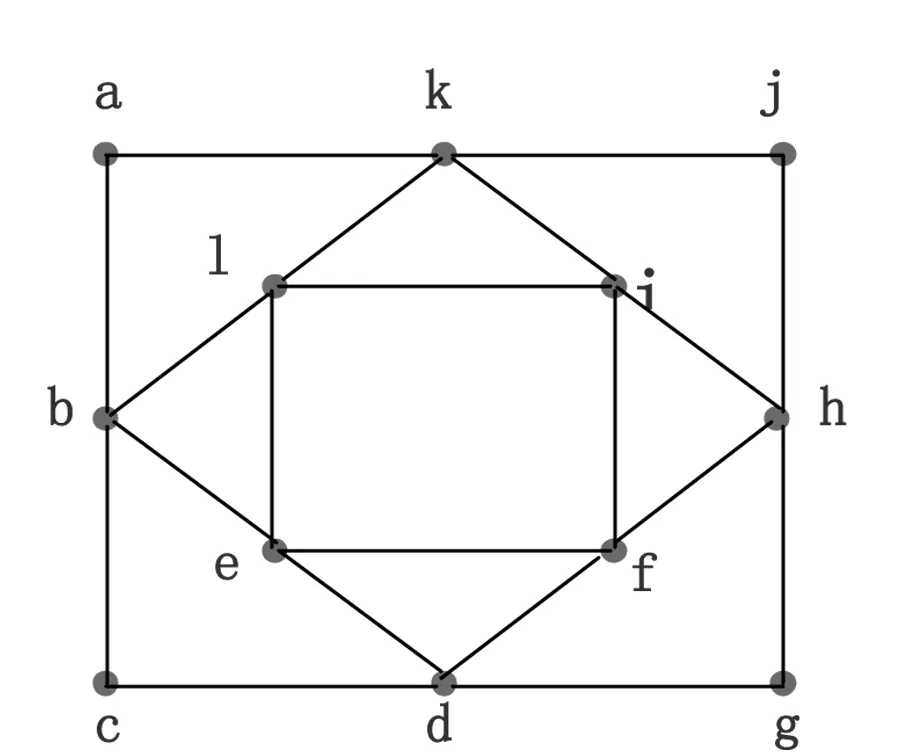
图1 一笔画问题
三、数学文化融入课堂教学
离散数学不仅仅包含抽象的概念和定理,也包含数学文明史,包含伟大数学家的创作经历,这些数学历史背景应该走进课堂,渗透到老师的实际教学中,让学生在学习的过程中受到感染,产生共鸣,体会离散数学的文化品位。
例如集合论是离散数学的重要组成部分,是现代数学中占有独特地位的一个分支。如何让学生理解集合、关系和函数的本质,教师可以结合集合论的起源,引入德国著名数学家Cantor和英国哲学家、数学家和逻辑学家Russell的故事,从世界数学家大会到第三次数学危机,从朴素的集合论到公理集合论,这些讲解会激发学生强烈的好奇心,使得学生既对Cantor的凄凉境遇打抱不平,又对他贡献无限尊敬和崇拜,转而让学生喜欢数学,热爱数学,想去为之探索和奉献。
这当然需要教师具有深厚的文化底蕴和平时不断积累,才能在离散数学教学中随心所欲地插入相关数学文化历史背景,将枯燥的定理概念和其具体的形成与发展有机地结合起来[3]。但是数学文化融入课堂不能喧宾夺主,它只是一味调剂,促使学生对所讲授领域的理解。
四、引入开放性教学实验
通过引入实验,使学生从程序设计的角度和课堂内容相结合,加深学生对概念与公式的理解和掌握。如在集合论教学中,偏序关系是其中的一个重要内容,但是教材偏重于从数学高度进行理论描述,从心理上增加了学生学习的难度,因此,我们尝试开放性实验教学,让学生设计算法判断偏序关系,并计算偏序集的特殊元素。
实验问题:给定二元关系R={
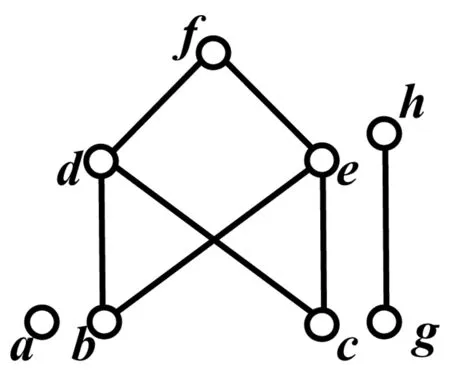
图2 R的哈斯图
借助计算机程序,通过实验过程,让学生验证自己的解题思路和结果,如图3所示。证明做对的感觉会激发学生的潜力,促使学生变被动为主动,不仅有助于充分理解老师的课堂教学内容,还很好地训练了学生的抽象思维能力、逻辑推理能力和运用数学知识分析解决实际问题的能力。利用信息技术,让学生亲自动手实践理解概念和定理,领悟数学在各个领域的精彩应用,这才是我们教学的真谛。
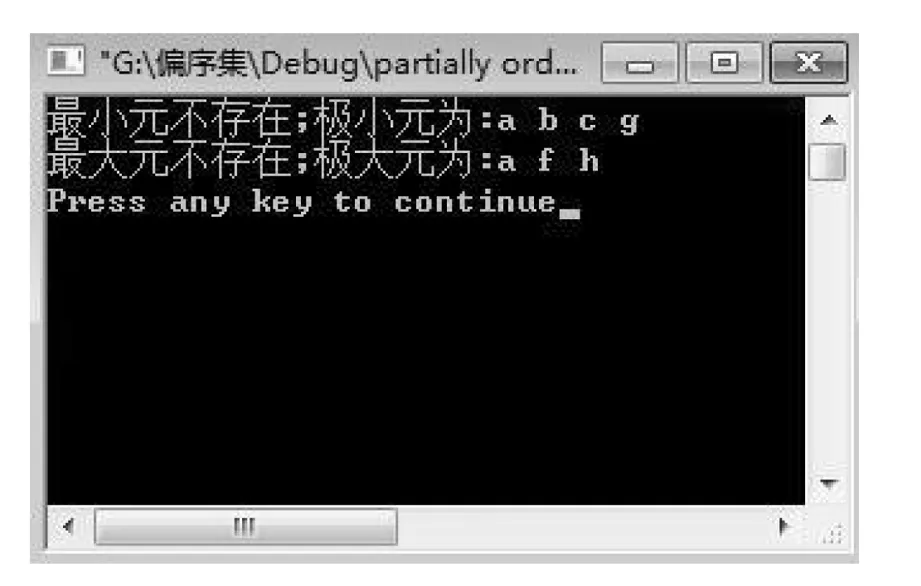
图3 偏序集的特殊元素
内容拓展:实验总结后老师还可以将内容拓展引申,让学生进一步加以探索。如当一个偏序集的每对元素都有最小上界和最大下界时,这个偏序集就称为格,可以使用格的模型表示不同的信息流策略。从而为我们后续学习布尔代数打下良好的基础。
五、结语
在离散数学课堂教学中融入数学文化,给离散数学这道大餐添加调料,使学生吃起来更美味,再辅以孔子“启发式”的教育理念,教师引而不发,点到为止,迫使学生动脑筋去思考,培养他们的创新能力,同时也快速提升教师的教学水平。通过实验拓展学生理解问题的深度和高度,使抽象、枯燥的数学问题变得直观、形象,克服学生的畏难情绪,培养学生对数学的理解和欣赏[4]。
参考文献:
[1] 屈婉玲,耿素云,张立昂.离散数学[M].北京:高等教育出版社,2008.
[2] 刘冬明.孔子的教学思想在离散数学中的应用[J].计算机教育,2010,(6):112~114.
[3] 刘卫锋,刘林,王东晓,等.数学文化融入离散数学的教学研究[J].计算机教育,2011,(6):52~55.
[4] 赵治国,刘丽.利用信息技术深化数学实验教学[J].中国电化教育,2011,1(288):110~112.
