偏态分布下多维测验合成信度区间估计的比较

叶宝娟 杨 强

偏态分布下多维测验合成信度区间估计的比较

叶宝娟 杨 强

用合成信度能比α系数更准确地估计测验的合成信度。本文用模拟研究比较了两种估计多维测验合成信度置信区间的方法，结果发现用Delta法通过近似计算得到的标准误，与Bootstrap法的结果差别很小，而且比Bootstrap法简单得多，因此推荐使用Delta法估计多维测验合成信度的置信区间。

多维测验；合成信度；置信区间；Bootstrap法；Delta法

用合成信度能比α系数更准确地估计测验的合成信度。[1][2][3][4]信度是一个总体参数，其值未知，在实证研究中通常用样本信度来估计。低信度的测验分数包含大量误差，对于许多研究来说是有问题的。[5]在评价测验质量时，点估计得到的信息有限，最好用信度的区间估计补充信度点估计得到的信息，以此得到在所研究的总体上重复取样时信度的精确性。[6][7][8]应用研究中经常碰到多维测验（multidimensionaltest），即整个测验测量了不止一个潜变量。叶宝娟和温忠麟用Delta推导出计算多维测验合成信度置信区间。[9]不仅如此，杨强、叶宝娟和温忠麟比较了测验题目为正态分布时，两种估计多维测验合成信度置信区间的方法：Bootstrap法和Delta法，结果发现Delta法是一种简单而准确的估计多维测验合成信度置信区间较好的方法，推荐用这种方法估计多维测验合成信度的置信区间。[10]那么，当测验题目为偏态分布时，Delta法的表现如何，是否可以用来估计多维测验合成信度的置信区间呢？本文将对此进行探讨。

本文首先简单介绍了多维测验合成信度及估计多维测验合成信度置信区间的两种方法：Bootstrap法和Delta法，然后用蒙特卡洛（Monte Carlo）模拟研究比较两种估计多维测验合成信度置信区间的方法，进而推荐比较好的方法估计多维测验合成信度的置信区间。

一、多维测验的合成信度

若一个测验由p个题目x1，x2，…，xp测量了n个潜变量F1，F2，…，Fn，δ1，δ2，…，δp为x1，x2，…，xp的测量误差，则有

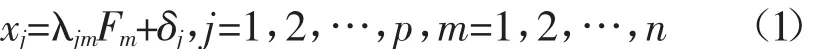
其中，λjm表示题目j在第m个潜变量上的负荷。

假设合成总分是有意义的，则整份测验X= x1+x2+…+xp的合成信度为[11][12]

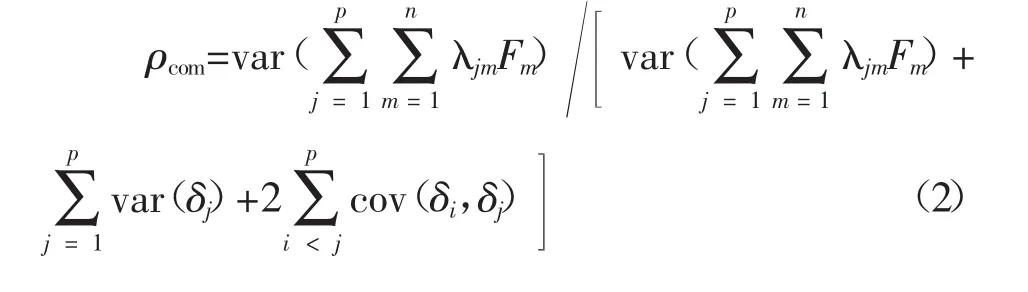
二、估计多维测验合成信度置信区间的方法

1.Bootstrap法

用Bootstrap法需要对一个固定的样本（当作总体）进行重复取样，比较麻烦，但计算的结果是一种实证结果，通常作为真值的反映，可以用来比较其他方法计算结果是否合理。Bootstrap法有多种取样方案，本文所说的Bootstrap法是从一个给定的样本中有放回地重复取样以产生出许多样本，即将原始样本当作总体，从这个总体中重复取样以得到类似于原始样本的Bootstrap样本。[13]这种方法比较麻烦，一般的应用工作者不易掌握。

2.Delta法

用Delta法估计多维测验合成信度的的标准误为

三、研究设计

本研究考虑以下变量：题目分布、因子个数、每个因子题数、因子相关、因子负荷、样本容量、估计方法。

（1）题目分布：设置的题目分布分别为均匀分布、χ2（3）分布。（被试间因素）

（2）因子个数：设置的因子个数为2、4。（被试间因素）

（3）因子相关：设置两个因子之间的相关在0～0.60之间，分为3种情况：高相关（0.40～0.60）、中相关（0.20～0.40）、低相关（0～0.20）。（被试间因素）

（4）每个因子上题数：设置的题数为3、6、10。（被试间因素）

（5）因子负荷：设置的因子负荷在0.30～0.90之间，分为3种情况：高负荷（0.70～0.90）、中负荷（0.50～0.70）、低负荷（0.30～0.50）。（被试间因素）

（6）样本容量：设置的样本容量分别为300、500、1000。（被试间因素）

（7）估计方法：Bootstrap法和Delta法。（被试内因素）

本模拟实验是一个2×2×3×3×3×3×2的设计，共有324种水平组合。

在每种处理（即水平组合）中，模拟一批数据，然后随机取一个拟合好的样本，即RMSEA和SRMR小于0.08，NNFI和CFI大于0.90，用Delta法和Bootstrap法计算合成信度的标准误。比较两个标准误的差异，也就是比较了合成信度的置信区间的差异。并且还可以了解当测验题目、因子负荷和样本容量变化时，合成信度的置信区间及其不同方法的差异是如何变化的。

四、研究结果

计算用Bootstrap法得到的标准误时，只使用收敛到恰当解且模型拟合较好的样本的结果。因为Bootstrap法得到的标准误是一种实证结果，可以看作是真值，因而可以将Delta法计算的标准误与其比较来计算偏差。比较的标准与单维测验比较的标准相同，也就是说，如果标准误相差0.01，信度的下限就会相差0.02。从应用角度看，如果信度下限相差0.01（相应的标准误相差0.005），表明只是微小差别；如果信度下限相差0.02（相应的标准误相差0.01），表明有点差别；如果信度下限相差0.05（相应的标准误相差0.025），则表明有实质差别。

1.均匀分布模拟研究结果

在均态分布下设计的162个处理条件中，有143个处理条件对应的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例为100%。除在4因子3个题目的因子相关低时，样本容量为300的负荷分别为低、中、高的3个处理的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例在80%以上但不足90%外，其余16个处理条件对应的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例都在90%以上。因为Bootstrap法赖以计算的样本不少于800个,所以计算结果有效。

（1）Delta法的标准误

比较Delta法和Bootstrap法的结果（参见图1）。Delta法的标准误偏差（绝对值）有正有负，但都很小，均小于0.005，在因子负荷为高时，标准误偏差均小于或等于0.001，尤其是在因子个数为4，题数较多（6，10）、因子负荷为高时，标准误偏差为0。因此，可以认为Delta法估计的标准误是近似无偏的。

（2）合成信度的标准误变化情况

保持其他条件不变，随着因子个数的增加，用Bootstrap法估计的标准误会变小。保持其他条件不变，随着因子相关的增加，用Bootstrap法估计的标准误不一定减小。保持其他条件不变，随着题目个数的增加，用Bootstrap法估计的标准误减小。保持其他条件不变，随着负荷的升高，用Bootstrap法估计的标准误减小。保持其他条件不变，随着样本容量的增加，用Bootstrap法估计的标准误减小。

总之，因子越多、题目越多、负荷越高或者样本容量越大，合成信度的标准误越小，从而估计的合成信度越精确。容易看出，用Delta法得到的标准误与用Bootstrap法得到的标准误变化情况一致。

图1 用Delta法和Bootstrap法计算的合成信度标准误的差值箱型图

2.χ2（3）分布模拟研究结果

在χ2（3）分布下设计的162个处理条件中，有142个处理条件对应的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例为100%。除在4因子3个题目的因子相关低时，样本容量为300的负荷分别为低、中的处理，及样本容量为500的负荷为低的处理的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例在80%以上但不足90%外，其余17个处理条件对应的Bootstrap样本，有恰当解且结构模型拟合较好的样本比例都在90%以上。因为Bootstrap法赖以计算的样本不少于800个,所以计算结果有效。

（1）Delta法的标准误

比较Delta法和Bootstrap法的结果（参见图2）。Delta法的标准误偏差（绝对值）有正有负，但都很小，均小于0.005，在题目较多（6,10）、因子负荷为高时，标准误偏差均小于或等于0.001。因此，可以认为Delta法估计的标准误是近似无偏的。

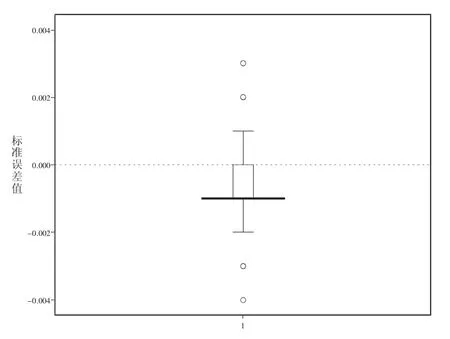
图2 用Delta法和Bootstrap法计算的合成信度标准误的差值箱型图

（2）合成信度的标准误变化情况

保持其他条件不变，随着因子个数的增加，用Bootstrap法估计的标准误会变小。但是有两个例外，在因子相关为低、中相关，题数为3，样本容量为300，因子负荷为低时，4个因子的样本的标准误比两个因子的样本的标准误大。这可能与在这两种情况下，Bootstrap法有恰当解且结构模型拟合较好的样本百分比不同有关。

保持其他条件不变，随着因子相关的增加，用Bootstrap法估计的标准误减小。保持其他条件不变，随着题目个数的增加，用Bootstrap法估计的标准误减小。保持其他条件不变，随着负荷的升高，用Bootstrap法估计的标准误减小。保持其他条件不变，随着样本容量的增加，用Bootstrap法估计的标准误减小。

总之，因子越多、相关越高、题目越多、负荷越高或者样本容量越大，合成信度的标准误越小，从而估计的合成信度越精确。容易看出，用Delta法得到的标准误与Bootstrap法得到的标准误变化情况一致。

3.模拟研究小结

相比于Bootstrap法，Delta法估计的标准误是比较精确的，而LISREL输出的标准误有较大的偏差。因此，可以使用Delta法计算合成信度的置信区间。

因子越多、题目越多、负荷越高或者样本容量越大，合成信度的标准误越小，从而估计的合成信度越精确。用Delta法得到的标准误与Bootstrap法得到的标准误变化情况一致。

五、结论

（1）Delta法的标准误与Bootstrap法的标准误差异很小。Bootstrap法的结果是一种实证结果，可以作为真值看待，但Bootstrap法计算过程相当麻烦，尤其是在题目很多，模型比较复杂时，计算机进行较大样本的Bootstrap抽样需要很长时间。Delta法通过近似计算得到标准误，与Bootstrap法的结果差别很小，而且比Bootstrap法简单得多。因此，推荐使用Delta法估计多维测验合成信度的置信区间。

（2）随着因子个数的增加、题目个数的增加、负荷的升高或样本容量的增多，用Bootstrap法（还有Delta法）估计的多维测验合成信度的标准误倾向于减小。

［1］温忠麟，叶宝娟.测验信度估计：从α系数到内部一致性信度［J］.心理学报，2011，43（7）：821～829.

［2］叶宝娟.偏态分布下单维测验合成信度三种区间估计的比较［J］.教育测量与评价，2012（10）：28～32.

［3］［7］叶宝娟，温忠麟.单维测验合成信度三种区间估计的比较［J］.心理学报，2011，43（4）：453～461.

［4］［8］［9］叶宝娟，温忠麟.用Delta法估计多维测验合成信度的置信区间［J］.心理科学，2012，35（6）：1213～1217.

［5］Lucas,R.E.,&Donnellan,M.B.EstimatingtheReliability of Single-Item Life Satisfaction Measures：Results from Four National Panel Studies［J］.Social Indicators Research, 2011,105（3）：323～331.

［6］Raykov,T.,&Shrout,P.E.Reliability of scales with general structure：Point and interval estimation using a structuralequationmodelingapproach［J］.StructuralEquationModeling,2002,9（2）：195～212.

［10］杨强，叶宝娟，温忠麟.两种估计多维测验合成信度置信区间方法比较［J］.心理学探新，2014，34（1）：43～47.

［11］屠金路，王庭照，金瑜.结构方程模型下多因子非同质测量合成分数的信度估计［J］.心理科学，2010，33 （3）：666～669.

［12］Yang,Y.,&Green,S.B.A Note on Structural Equation Modeling Estimates of Reliability［J］.Structural Equation Modeling,2010,17（1）：66～81.

［13］Wen,Z.,Marsh,H.W.,&Hau,K.T.Structural E－quationModelofLatentInteractions：AnAppropriateStandardizedSolutionandItsScaleFreeProperties［J］.StructuralEquationModel,2010,17（1）：1～22.

责任编辑/王彩霞

G40-058.1

A

1674-1536（2014）11-0008-04

本研究获得教育部人文社会科学研究青年基金项目（13YJC190029）、全国教育科学规划教育部重点课题“均等化视角下的省级义务教育政策绩效评估研究”（DFA130249）、江西省高校人文社会科学研究项目（JY1320）资助。

叶宝娟/江西师范大学心理学院教师，江西师范大学心理学院博士后。（南昌 330022）

杨 强/江西师范大学教育学院教师。