战术导弹对机场跑道多波次打击时的瞄准点选择方法

卜广志，张 斌，师 帅

（北京系统工程研究所复杂系统仿真总体重点实验室，北京 100101）

战术导弹对机场跑道多波次打击时的瞄准点选择方法

卜广志，张 斌，师 帅

（北京系统工程研究所复杂系统仿真总体重点实验室，北京 100101）

为了解决使用战术导弹对机场跑道实施多波次打击时的瞄准点选择问题，在考虑具有先前毁伤效果的累积效应基础上，按照优先打击最小起降窗口、使最小维修窗口中维修工作量最大的思路，设计了一种瞄准点选择方法，可为相应的导弹作战运用提供参考。所附算例说明了文中方法的可行性。

战术导弹，瞄准点，机场跑道，多波次打击

引言

在现代高技术条件下的战争中，通过直接打击敌方机场、使其飞机无法正常起降，从而夺取制空权的作战是掌握战争主动权的重要组成部分，甚至会影响整个战争的胜负。战术弹道导弹具有难于拦截、精度高、不会造成人员损失等优点，在打击机场时，尤其是第一波次高危条件下的打击时，可作为优先运用的装备。同时，现代机场都配有多种抢修措施，在跑道遭受毁损时，经过抢修很快就会重新投入运转，正常起降飞机。因此，使用战术导弹对机场跑道必须持续多波次打击，才能实现预期的压制效果。

在战术导弹的战术运用中，由于导弹性能及作战中随机因素的存在，导弹实际落点不可能与瞄准点完全一致，因此，瞄准点的选择对实际毁伤效果具有非常大的影响。当实施多波次打击时，由于存在先前的毁伤，此时必须考虑毁伤效果的累积效应，才能选择出合适的瞄准点，使较少的导弹能够发挥出较大的作战效能。本文针对此问题，按照确保没有最小起降窗口、使最小维修窗口的维修工作量最大的思路，重点研究多波次打击机场跑道时，在对跑道已有一定毁伤的后续打击中，对导弹瞄准点的选择方法。

1 多波次打击中瞄准点选择的特点

使用战术导弹对机场跑道进行打击，通常会选择携带子母弹的弹头，抛撒出来的子弹对跑道会造成多个弹坑或隆起。如果这些弹坑间的未损区域无法满足飞机的最小起降窗口大小，飞机便无法正常起降，从而达到压制机场的目的。由于机场跑道的这种重要性，通常每个机场都配有跑道抢修分队和相应的快速维修系统。当跑道遭受打击出现毁损时，通过清理弹坑或隆起，快速浇注水泥，或铺设钢板等方式，能够在较短时间内，使飞机恢复正常起降。因此，对机场跑道必须实施多波次打击，及时补充打击未成功封锁的跑道或已修复的跑道部分。

对于第一波次打击中瞄准点的选择方法，已有很多的研究［1-3］。本文重点研究第二波次以后的打击中，在先前毁伤效果基础上，对瞄准点的选择方法。此时，根据毁损和维修情况，跑道可能具有两种情形：①可以起降飞机，包括先前打击后未实现压制和实现压制后，经抢修又恢复起降功能；②无法起降飞机，包括实现压制后未进行修复，或经修复仍未能恢复功能。对于第1种情况，后续打击的目标是要优先实现压制封锁，使机场跑道不具有最小起降窗口。对于第2种情况，后续打击的目标是要增加维修工作量，使之更难于修复。此处，假设维修工作量正比于弹坑数，并引入最小维修窗口的概念，即在机场跑道上，不小于最小起降窗口的一个区域，且该区域中需要维修的弹坑数量最少。这样，第2种情况的打击目标即是使最小维修窗口中的弹坑数尽可能多。

在实际作战中，为了及时、准确评估对机场跑道的毁损情况，需要具有相应的战场监视手段，才能获得实际的弹坑位置信息，进行瞄准点的选择。当不具备这样的毁损信息时，可以假定先前的打击效果是理想的，即子弹形成的弹坑在瞄准点周围，抛撒半径范围内成均匀分布。

2 考虑累积效应的瞄准点选择方法

2.1 算法的框架

根据获得的跑道上弹坑分布位置信息或假设的理想分布情况，首先判断是否存在最小起降窗口，如果存在，便优先打击存在的最小起降窗口，否则，在导弹数量可用的前提下，反复打击最小维修窗口。整个算法流程如图1所示。

2.2 判断最小起降窗口的算法

假设机场跑道为长宽分别是L、W的矩形，以跑道中心位置为原点O建立坐标系。X轴沿跑道纵向，Z轴垂直地面向上，Y轴沿建立右手坐标系方向。最小起降窗口为长宽分别是l、w的矩形。为了简化分析，只考虑长度方向沿跑道X方向的最小起降窗口，不考虑与X轴成一定夹角的情况。

在经过前期打击后，跑道上的弹坑位置分别为（xi，yi）（i=1，2，…，N），N为对跑道造成毁损的弹坑数量。假设每个弹坑为一个半径为ri的圆形区域，隆起的部分也视为弹坑处理。

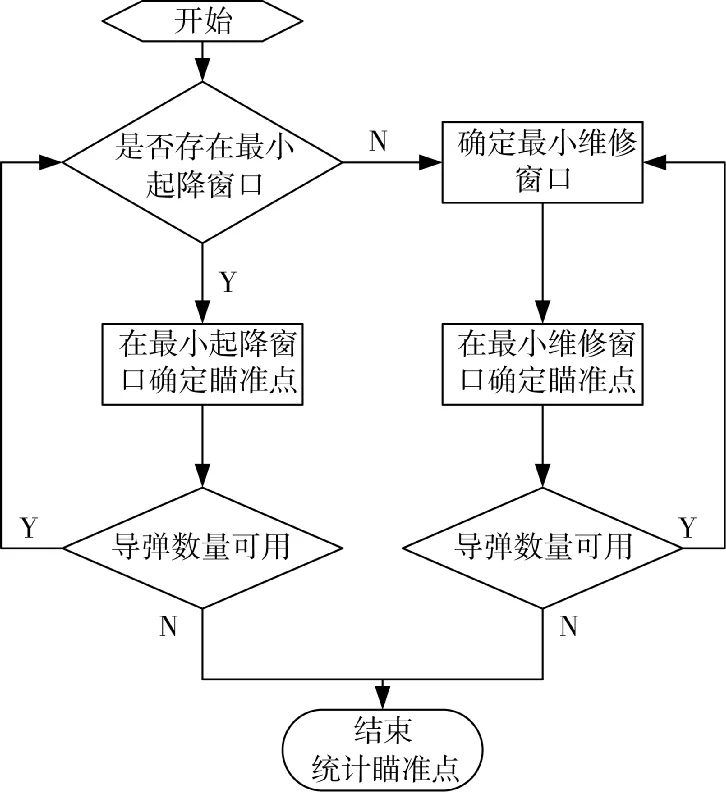
图1 算法框架

按照区域搜索法［4-5］，判断最小起降窗口的步骤如下：

（1）对所有弹坑位置的坐标，按照X坐标的升序进行排序，得到（xi'，yi'）（i=1，2，…，N）。

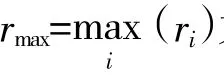
（3）下面介绍以第j个弹坑为起点，搜索是否存在最小起降窗口的方法，如图2所示。

图2 最小起降窗口的搜索区域

根据第j个弹坑的位置，搜索X方向上（xj'+rj'，xj'+rj'+l）范围内的弹坑在Y方向上，两两相邻间，或最靠近跑道弹坑与跑道边缘之间的完好区域宽度Δj是否不小于w。如果存在，则认为存在最小起降窗口；否则，不存在最小起降窗口。

假设此范围内有Ns个弹坑，将其坐标按照Y坐标升序排序为（xjs'，rjs'），则

如果Δj＜0，即两个弹坑在Y方向上过于靠近，则令其等于0。

（4）如果以第j个弹坑为起点不存在最小起降窗口，则将搜索区域移至下一个弹坑位置（x'j+1，y'j+1），直至x'j+r'j+l＞L/2时，搜索完毕。

值得注意的是，跑道上的最小起降窗口可能是多个。按照此算法，实质上是沿着X轴方向依次进行搜索。所以，在设定一个瞄准点后，如果导弹数量可用，需重新搜索是否存在其他的最小起降窗口。

2.3 确定最小维修窗口的算法

与判断最小起降窗口的算法类似，区别在于第（3）步中，依次判断该区域内，两两弹坑之间、每个弹坑与跑道边缘之间大于w宽度的区域内，存在的最小弹坑数，如图3所示。具体算法如下：

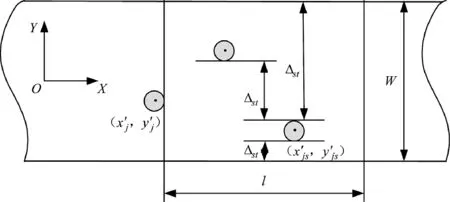
图3 最小维修窗口的搜索区域

弹坑s（s=1，2，…，Ns）与弹坑t（t=s，s+1，s+2，…，Ns+1）之间，或与跑道边缘之间的区域宽度：

如果Δst＜0，则令其等于0。

当Δst≥w时，计算该区域存在的弹坑数：

在第（4）步中，持续搜索最小维修窗口中的弹坑数，直至x'j+r'j+l＞L/2时，搜索完毕。

2.4 设定瞄准点的方法

按照最小起降窗口、最小维修窗口的判断算法，瞄准点选择在窗口的中心点位置较为适宜，能够达到确保破坏最小起降窗口，或增加最小维修窗口中弹坑数量的目的。

在图1所示的算法框架内，只要导弹数量可用，就会反复搜索最小起降窗口或最小维修窗口，所以要确定的瞄准点数量就是此波次打击中使用的导弹数量。随着每次设定一个瞄准点，这些窗口的位置和数量也会发生变化。为了简化分析，新加入的瞄准点在下次搜索中，可视为准确命中了一枚导弹，子弹在瞄准点周围的抛撒半径范围内均匀分布。

3 算例

假定使用7枚战术导弹对一机场跑道目标进行压制打击，第一波次发射4枚，第二波次发射3枚。跑道长3 000 m，宽50 m。最小起降窗口长1 600 m，宽15 m。导弹圆概率误差40 m，子弹抛撒半径50 m，子弹个数80枚，杀伤半径1 m。现求解第二波次打击时，3枚导弹的瞄准点位置。

由于导弹实际落点与瞄准点之间存在误差，因此，这里给出的结果只是众多可能情况中的一种。在第一波次打击后，假定命中跑道的弹坑分布位置如图4所示（注：为了便于标注，对图中跑道的长宽比进行了调整）。

图4 弹坑分布与瞄准点的选择

按照本文中的算法，根据对弹坑分布的判断，不存在最小起降窗口。此时，最小维修窗口位于（-1 500，-25）、（100，-10）为对角线的矩形区域（图4中三角形为顶点的矩形），其中具有4个弹坑，瞄准点选择在（-700，-17.5）位置。对于第2枚、第3枚导弹的瞄准点，选择打击的最小维修窗口分别是（-341.07，-25）、（1258.93，-10）和（-1500，-6.41）、（100，8.59）为对角线的矩形区域（图4中菱形、正方形为顶点的矩形），其中分别具有19个、23个弹坑，瞄准点分别选择在（458.93，-17.5）、（-700，1.09）位置。

从瞄准点选择的顺序可以看出，对第二波次发射的3枚导弹所依次打击的最小维修窗口，需要维修的弹坑数量在不断增多，即文中的瞄准点选择方法可以确保对跑道的维修工作量不断增大。

4 结 论

在使用战术导弹对机场跑道进行多波次打击时，针对第二波次以后打击中的瞄准点选择问题，本文在考虑先前毁伤效果的基础上，设计了瞄准点选择的算法。其中，针对弹坑命中位置的分析，优先打击可能存在的最小起降窗口，然后在导弹数量可用的前提下，再依次打击最小维修窗口。这种算法可以快速定位最小起降窗口和最小维修窗口的位置，使得瞄准点的选择有助于最大程度地发挥有限数量导弹的效能，可用于支撑导弹的战术运用。同时，本文的瞄准点选择方法也适用于航空兵使用空地制导弹药对跑道的瞄准点选择问题。

［1］舒健生，陈永胜.对现有跑道失效率模拟模型的改进［J］.火力与指挥控制，2004，29（2）：99-102.

［2］寇保华，杨 涛，张晓令，等.末修子母弹对机场跑道封锁概率的计算［J］.弹道学报，2005，17（4）：22-26.

［3］黄龙华，冯顺山，王震宇.多模式封锁弹对机场跑道封锁效能的分析［J］.弹箭与制导学报，2006，26（4）：173-176.

［4］黄寒砚，王正明.子母弹对机场跑道封锁时间的计算方法与分析［J］.兵工学报，2009，30（3）：295-300.

［5］David A S，David T O，Toy I R，etc.A Question of Balance: Political Context and Military Aspects of the China-Taiwan Dispute［R］.RAND Corporation，2009.

Aimpoints Selection Method Multiwave Attack Runway with Ballistic Missiles

BU Guang-zhi，ZHANG Bin，SHI Shuai
（Science and Technology on Complex Systems Simulation Laboratory，Beijing 100101，China）

In order to gain a significant attacking level of the runway with ballistic missiles，multi waves need to be fired iteratively at an interval.Then，how to assign the missile aimpoints becomes an important aspect in the missile operation.This paper designs an aimpoints selection method based on the previous impacts.If previous missile strike did not attack runway successfully，the aimpoint need to be assigned to the minimum operating strip firstly;otherwise，the aimpoint is to be assigned to the minimum repairing strip.The number of aimpoints is equal to that of missiles to be fired.The followed example verifies this tactic.

ballistic missile，aimpoint，runway，multiwave attack

TJ762.2；TU248.6

A

1002-0640（2014）11-0064-03

2013-08-05

2013-11-27

卜广志（1974-），男，辽宁北镇人，博士，副研究员。研究方向：武器装备体系技术、建模与仿真技术。