地空导弹发控系统寿命预测的组合模型
2014-06-15雷荣强孙安全
雷荣强,舒 涛,孙安全,张 琳
(空军工程大学防空反导学院,西安 710051)
地空导弹发控系统寿命预测的组合模型
雷荣强,舒 涛,孙安全,张 琳
(空军工程大学防空反导学院,西安 710051)
将灰色系统理论和BP神经网络有效地结合起来,建立了灰色BP神经网络的组合预测模型,并采用遗传算法对该模型进行优化。为了验证优化后模型的有效性,采用灰色BP神经网络的预测结果进行对比分析。实际数据的预测结果表明,优化之后的模型比单独采用灰色BP神经网络,具有更小的均方差(MSE,Mean Square Error),对发控系统剩余寿命(RUL,Remaining Useful Life)也具有更高的预测精度。
灰色系统理论,BP神经网络,遗传算法,寿命预测
引言
导弹发控系统完成导弹发射前支撑,并与其他设备一起,协同完成发射前准备工作;发射时赋予导弹以规定的发射角度;发射后与装弹设备一起完成导弹装填。导弹发射架为用于悬挂和发射导弹的专用装置。
设备的寿命预测就是在设备的使用过程中,利用设备历史数据、当前信息和环境条件,准确及时判断其运行状态并预测其运行状态的发展趋势,为设备的使用和维护提供决策性依据[1]。对系统关键部件剩余寿命的准确预测能有效预防系统故障的发生,使工程人员根据系统的运行情况合理规划和实施维修计划,从而避免过度维修,降低寿命期内的维修成本。目前常用的预测方法主要有回归预测、时间序列预测、灰色理论预测、人工神经网络预测等方法。文献[2]对这几种方法的优缺点进行了详细的比较。
灰色预测模型适用于单一指数增长模式序列,对数据出现异常的情况预测效果欠佳。人工神经网络具有非线性模式分类性能和强大的自学习功能,可通过学习过程准确处理数据,实现对某些异常情况的预测[3]。因此,本文将灰色预测方法与神经网络预测方法相结合,建立灰色神经网络预测模型。为了进一步提高预测精度,采用遗传算法对神经网络的权值阈值进行优化。
1 发控系统寿命预测灰色BP神经网络预测模型
利用GM(1,1)模型对原始序列进行模拟得到模拟序列,再将模拟序列作为BP神经网络的输入样本进行训练得到残差序列,两者之和构成新的预测序列,这样可以将灰色系统模型善于处理小样本数据和BP神经网络优于解决复杂非线性问题的优点有效地结合起来,提高费用预测的灵敏度。
1.1 GM(1,1)模型
将原始数据序列X(0)进行一次累加后可生成序列:
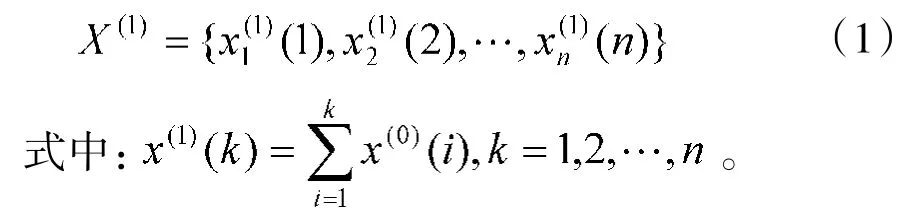
构造灰色微分方程:
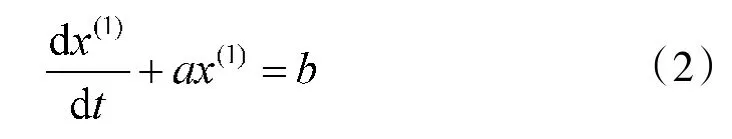
式中:a称作发展系数,其大小反映了序列x(0)的增长速度,b为灰色作用量。a和b的值可通过最小二乘法求的。其具体步骤可参考文献[4]。
参数a和b确定之后,即可进行GM(1,1)模型的选取,通常涉及的模型有定义型、内涵型和白化型,这里选取白化模型,其灰色预测模型为:

灰色模拟值为:

将实际值与预测值相减即可获得残差数据序列:
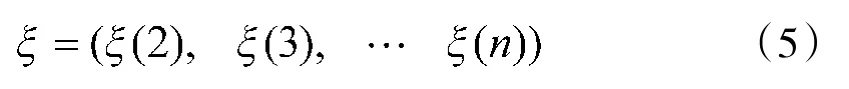
1.2 灰色BP神经网络组合预测模型建立
BP神经网络是利用非线性可微分函数进行权值训练的多层前馈网络,它具有3层或3层以上的神经网络,包括输入层、隐含层和输出层,其上下层之间可以实现全连接,并且每层神经元之间无联系,使得容错抗错性能和非线性映射能力强[5]。
1.2.1 建模步骤
将发控设备残存序列看作是一个非线性的时间序列,构造BP神经网络的输入输出模式对,从而实现对时间序列对象的预测目的。其模型计算步骤如下[6]:
(1)用选定的原始数据组成的序列构建GM(1,1)模型;
(2)用GM(1,1)模型预估序列的第2到第n个数据,得到长度为n-1的数据序列P。将实际序列与预测序列的对应量相减即可获得长度为n-1的残差数据序列数据ξ;
(3)将序列P作为神经网络的输入序列,序列ξ作为神经网络的输出序列。在确定网络隐含层节点数及训练函数后,训练BP神经网络,得到网络中对应于每个结点的一系列权值和阈值;
(4)用第(1)步建立的GM(1,1)模型来预测,将这些预测值作为网络的输入进行仿真,得到相应的输出,即为灰色BP神经网络组合预估模型的结果。
1.2.2 隐含层数设计
Robert Hecht-nielsen证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的BP网络来逼近,而且,一般靠增加隐层节点数来获得较低的误差,其训练效果要比增加隐层数更容易实现。因此,本文采用3层BP神经网络(即输入层、输出层和1个隐含层)对实验数据进行学习。
1.2.3 隐含层节点数设计
隐层节点数的多少直接决定网络结构和误差曲面的分布,但到目前为止,没有一种成形的方法指导选择合适的隐层节点数。本文按照公式:

确定隐层节点数的取值范围,其中l为隐层节点数,n为输入节点数,m为输出层节点数,a为1~10之间的常数[7]。对不同节点数的网络分别建模训练,通过比较均方误差(Mean Square Error,MSE),取其中最小误差隐层节点数为最优隐层节点数。
1.2.4 传递函数和训练函数的选择
对于函数逼近的应用通常隐含层节点激活函数选择双曲正切S型可微函数tansig,可以将神经元的输入范围从(-∞,+∞)映射到(-1,+1)区间上;输出层神经元激活传递函数选择线性函数purelin[8]。
分别采用不同的训练函数对网络进行训练,根据其达到目标误差所用的训练时间来选择最优的训练函数。

表1 可靠度随使用次数变化表

表2 GM(1,1)模型预测预测结果
1.3 发控系统的寿命预测
以某地空导弹发控系统为例进行分析,其可靠度随使用次数的变化如表1所示。
根据GM(1,1)预测模型,以表1中的可靠度作为原始数据,通过计算可得可靠度随使用次数的变化值。表2所示给出了使用2次~10次时的可靠度预测值和残差值。
以表2中灰色模型预测的可靠度为BP神经网络进行训练时的输入向量,输入层节点数n=1;以残差为目标向量,输出层节点数m=1。进行预测时将灰色模型预测的第8次及其以后的预测值作为输入向量。


表3 不同节点数网络训练误差
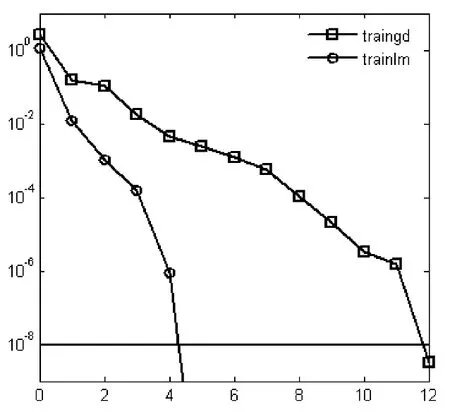
图1 训练函数trainlm和训练函数trainbfg下网络的性能曲线
当采用训练函数traingd对网络进行训练时,经过1 000次训练后的误差为5.303 8e-2,没有达到要求的目标误差。图1给出了在训练函数trainlm和训练函数trainbfg下网络的性能曲线,从图中可以看出:采用trainlm训练函数时,网络收敛快、训练误差低。故本文选择的训练函数为trainlm。
运用训练好的BP神经网络对8次~12次使用时,发控系统的可靠度进行预测,结果如表4所示。
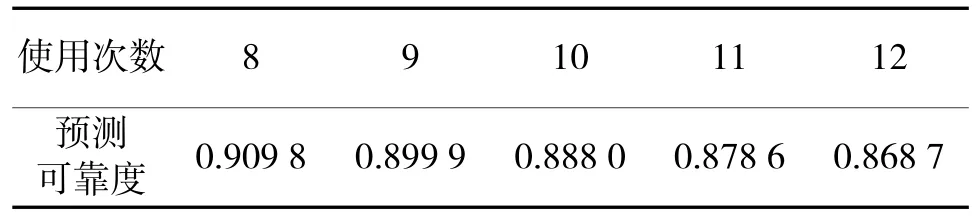
表4 灰色BP神经网络模型预测的可靠度随使用次数变化表
2 遗传神经网络学习算法
在传统BP神经网络中,其连接权值所采用的学习方法是一种梯度下降算法,使得网络容易陷入样本误差平方和的局部极小点。本文将遗传算法与BP网络有机结合起来,用遗传算法优化网络权值和阈值。
2.1 遗传神经网络设计
2.1.1 编码和初始化
采用实数编码,可降低算法的复杂度、提高算法的搜索能力。若神经网络结构为n-l-m(其中:n为输入层节点个数;l为隐层节点个数;m为输出层节点数),则生成若干个编码长度为(n+2)×l+m的染色体[9]。其中,前n×l位编码分别表示输入层到隐层的权值;后l位编码表示到输出层的权值,再后l位编码表示隐层各神经元的阈值,最后m位表示输出层的阈值。
2.1.2 遗传算法参数设置
确定权阈值搜索空间、确定群体规模N、遗传代数G、并初始化种群p(0),令k=0。本文设定群体规模为50,遗传代数为150,变异概率为0.05。
2.1.3 确定适应度函数
以BP神经网络的预测输出和期望输出之间的绝对误差和的倒数作为适应度函数F。
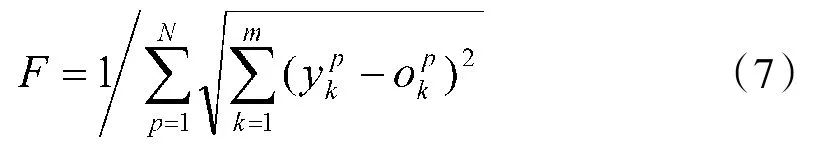
2.1.4 遗传操作设计
选择算子同时采用赌轮选择法和最佳个体保存法,将父代中适应度最高的个体不进行配对交叉而直接复制到下一代,并利用赌轮的方式对其余染色体进行选择;交叉算子采用算数交叉,2个配对的个体按照0.8的概率交换其中部分基因;变异算子采用均匀变异,以变异概率0.05从对应基因的取值范围内取一随机数代替原有的基因值。其详细设计方法可参考文献[10]。算法流程如下页图2所示。
2.2 发控设备寿命预测
仍取1.3中的输入输出序列即灰色理论模型的预测值和实际值与预测值的残差,作为经遗传算法优化后的灰色BP神经网络预测模型的输入、输出,并对该网络进行训练。仍采用1.3中的预测序列即灰色理论模型的预测值作为该网络在预测时的输入序列,表5给出了不同预测模型的均方差,从中可以看出,经过遗传算法改进后预测模型的均方差有着明显降低即具有更高的预测精度。
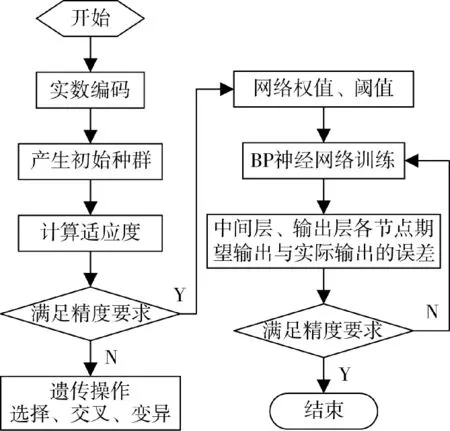
图2 遗传BP神经网络算法框图
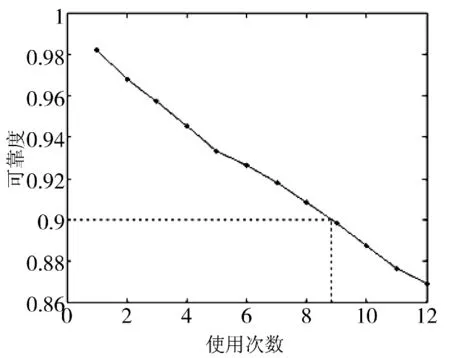
图3 寿命曲线

表5 不同预测模型预测结果均方差比较
经过遗传算法优化后的灰色BP神经网络模型在预测时得到如图3所示的寿命曲线。假定当发控设备可靠度R<0.9时寿命到期,由图可知,可靠度0.9出现在使用8次和9次之间,即可认为该发控设备在使用8次后寿命到期。与实际情况相符,结论可信。
3 结 论
(1)对灰色系统理论和BP神经网络模型进行了有机组合,融合了灰色系统模型善于处理小样本数据和BP神经网络优于解决复杂非线性问题的优点,克服了单一预测模型失效带来的预测误差,提高了预测可靠性和精度。
(2)用遗传算法对灰色BP神经网络预测模型中的权值阈值系数进行优化,建立了组合预测模型,达到较高的预测精度。并用该模型对某地空导弹发控系统的寿命变化趋势进行了预测,证明了利用该方法建立组合预测模型的可行性。
[1]梁 旭,李行善,张 磊.支持视情维修的故障预测技术研究[J].测控技术,2007,26(6):5-9.
[2]徐廷学,陈海建,滕克难,等.导弹贮存寿命预估的组合模型[J].火力与指挥控制,2011,36(10):124-127.
[3]刘 威,赵选民,邓春龙.灰色神经网络模型在海水腐蚀预测中的应用[J].中国腐蚀与防护学报,2008,28(4): 201-204.
[4]刘玉梅,蒋寿生,袁文华.锅炉过热器剩余寿命非等间隔灰色预测[J].中南大学学报(自然科学版),2010,41(3): 1202-1206.
[5]梁庆卫,赵民全,杨 璞.灰色神经网络的鱼雷经济寿命预测[J].火力与指挥控制,2011,36(10):172-175.
[6]何庆飞,陈桂明,陈小虎,等.基于改进灰色神经网络的液压泵寿命预测[J].中国机械工程,2013,24(4): 500-506.
[7]傅荟璇,赵 红.MATLAB神经网络应用设计[M].北京:机械工业出版社,2010:83-97.
[8]陈 娜,李 鹏,江 剑,等.中高压IGBT开关特性的遗传神经网络预测[J].电工技术学报,2013:28(2): 240-247.
[9]方 向,陆凡东,高振儒,等.中深孔爆破振动加速度峰值的遗传BP网络预测[J].解放军理工大学学报(自然科学版),2010,11(3):312-315.
[10]王德明,王 莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报(工学版),2012,46(5):838-841.
Research on Life Forecast Method of Missile Launching System Based on Combinatorial Model
LEI Rong-qiang,SHU Tao,SUN An-quan,ZHANG Lin
(Air Defense and Antimissile Institute,Air Force Engineering University,Xi'an 710051,China)
The paper puts forward a combined forecasting model based on grey system theory and Back Propagation(BP)neural network model,and Genetic Algorithm(GA)is used to optimize the weights and bias of BP neural network.A simulation example proves that the total error of the combined model's forecasting result is smaller than before,and can largely improve the forecasting precision of life prediction.
grey system theory,BP neural network,genetic algorithm,life prediction
TJ761
A
1002-0640(2014)11-0089-04
2013-09-25
2013-11-08
雷荣强(1989- ),男,陕西澄城人,在读硕士。研究方向:地空导弹发射系统测控技术。
