考虑弹塑性变形机制的结合面静摩擦因数模型
2014-06-13张学良温淑花陈永会兰国生刘丽琴太原科技大学机械工程学院太原030024
张 颖,张学良,姜 来,温淑花,陈永会,兰国生,刘丽琴(太原科技大学机械工程学院,太原 030024)
据美国材料试验学会ASTM的分析报告指出,全世界约有40%以上的各类能源被摩擦消耗掉,摩擦会引起一系列的物理和化学变化,产生热、噪音、振动、污染,甚至会引发危险。研究和预测机械系统的摩擦同样是非常重要的。而静摩擦因数是研究中摩擦的一个十分重要的参数。因此,关于结合面静摩擦因数的研究具有十分重要的意义。Chang等[1]人基于经典的G-W接触模型[2],通过考虑弹性接触点承受的切向载荷的能力,提出了金属表面间的静摩擦因数计算模型。Kogut和Etsion通过研究发现,结合面弹-塑性接触点同样具有承受切向载荷的能力,如果仅仅考虑弹性接触点承受切向载荷的静摩擦模型,显然对静摩擦因数的预测是不精确的。同时以上的研究都是建立在二维分形模型基础上的。应用二维的分形模型计算三维粗糙表面的接触特性,存在着理论上的不合理性[3]。鉴于此,文献[4]提出了一种基于三维接触分形理论的结合面静摩擦因数模型,但该模型没有考虑弹-塑性变形阶段对静摩擦因数的影响。
本文基于三维接触分形理论及文献[5]的弹塑性变形机制,综合考虑结合面微凸体的三种变形机制,从而建立了一种考虑弹-塑性变形的结合面静摩擦因数三维分形模型,并进行了仿真计算分析。
1 结合面三维分形接触模型
1.1 结合面三维建模
结合面实质就是两个粗糙表面的接触,在研究的过程中,为了简化通常将结合面的接触表示为一个刚性平面与一个粗糙平面的接触。当结合面受到挤压,微凸体将发生变形时,单个微凸体和刚性表面的弹性接触如图1所示。
结合面的复合弹性模量为:
式中,E*为两接触材料的复合弹性模量;E1、E2为两接触材料的弹性模量;v1、v2为两接触材料的泊松比。
在该模型中假设了微凸体的分布是各向同性的,

图1 单个微凸体与刚性平面弹性接触示意图
微凸体之间的相互作用忽略不计,并且没有宏观的变形,变形过程只发生在微凸体上。
根据文献[3]的研究结果可知,当法向变形量δ处于不同范围时,微凸体将发生完全弹性变形、弹-塑性变形及完全塑性变形。
单个微凸体的圆形接触面积a、截断面积a′和法向接触载荷Pe,当微凸体的变形在完全弹性变形阶段时可以表示为:
(1)
ae=πRδ
(2)
其中下标e表示发生弹性变形。
当微凸体的变形在弹-塑性变形阶段时,弹-塑性变形区域的范围为δc≤δ≤110δc,并将弹-塑性区域进一步划分为两个区域:弹-塑性变形第一区域(δc≤δ≤6δc)和弹-塑性变形第二区(6δc≤δ≤110δc).微凸体弹-塑性变形阶段法向接触载荷、接触面积和变形量之间的关系为[5]:
(3)
(4)
(5)
(6)
式中下标ep1、ep2分别表示发生弹-塑性第一区变形、弹-塑性第二区变形。
弹性临界变形量δc为[5]:
(7)
当微凸体的变形在完全塑性变形时,微凸体的变形量在δp>110δc范围内,微凸体在塑性变形阶段的接触面积和法向接触载荷Pp可以表示为:
Pp=Hap
(8)
ap=a′
(9)
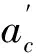
(10)
粗糙表面上的横截微凸体大小分布函数为[3]:
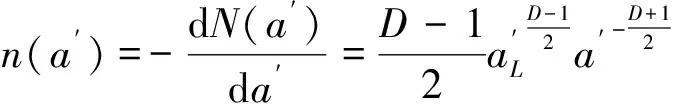
(11)

结合面真实接触面积Ar通过积分得到:
(12)
1.2 结合面法向载荷计算模型
微凸体的变形量δ是由W-M函数所决定的,其值取决于余弦函数的波峰和波谷的幅值,即[3]:
(13)
微凸体的变形量δ、微接触点的截半径r′、微凸体的曲率半径R的几何关系为:
(R-δ)2+(r′)2=R2
(14)
又因为δ<<2R,所以:
(15)
将式(13)代入式(15)得[3]:
(16)
结合面法向载荷与真实接触面积之间的关系式为:
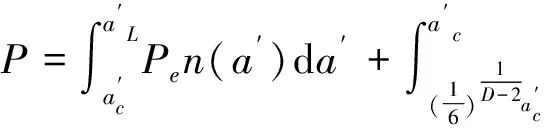
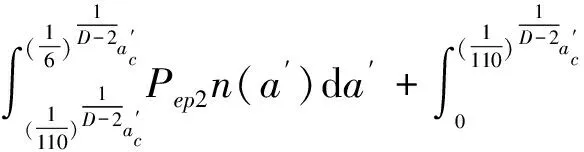
(17)
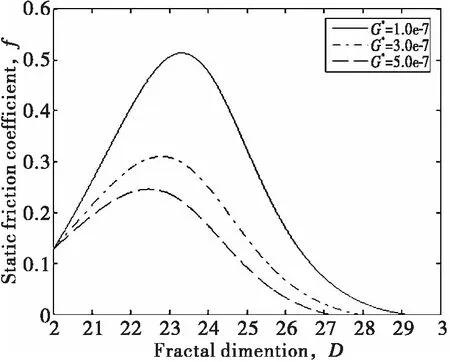
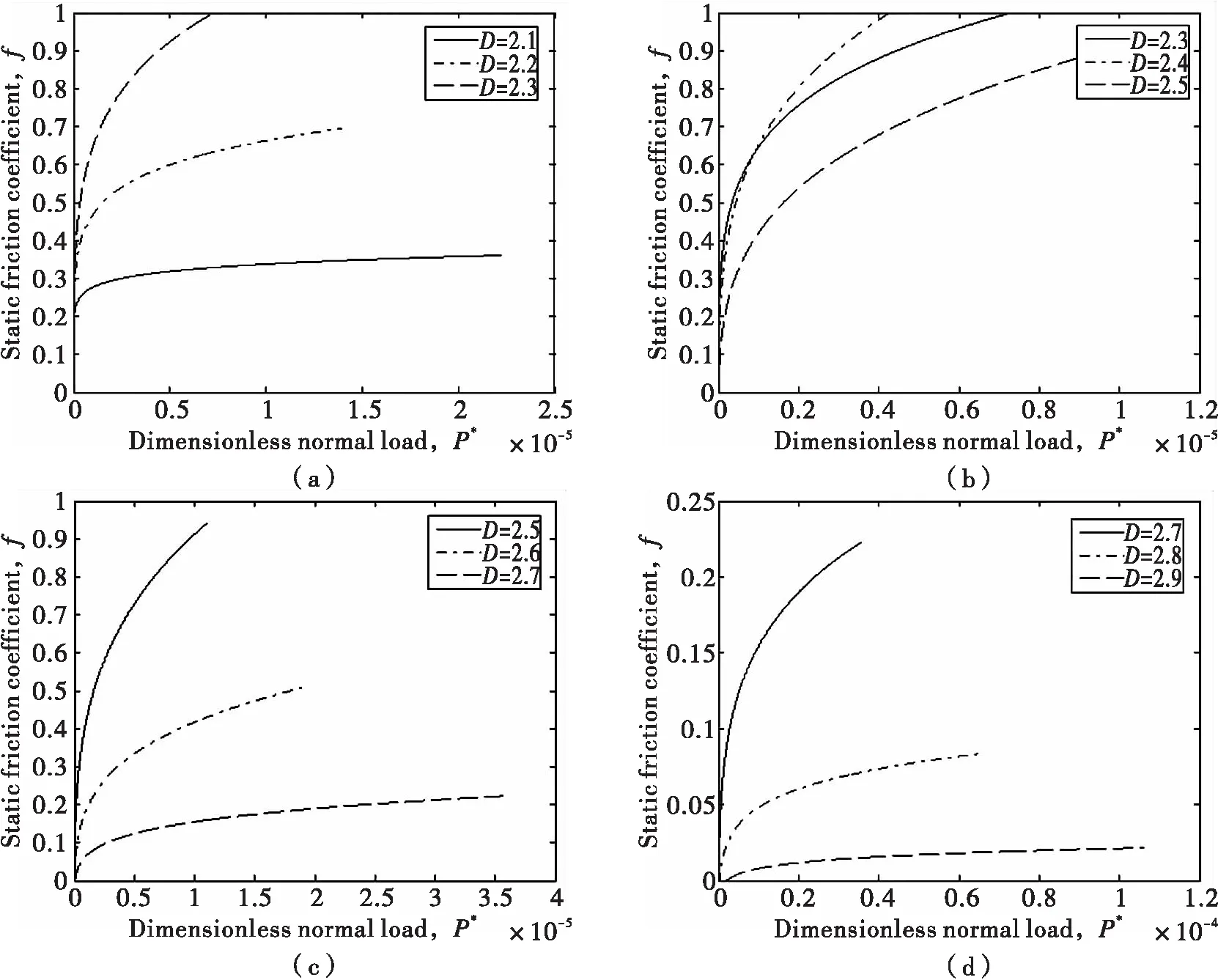
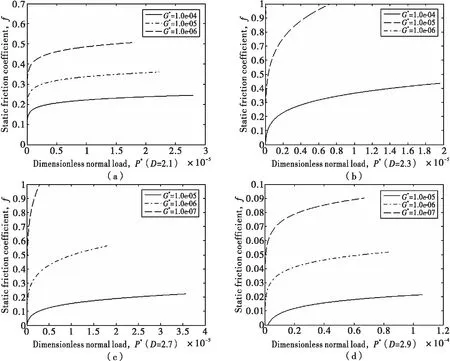
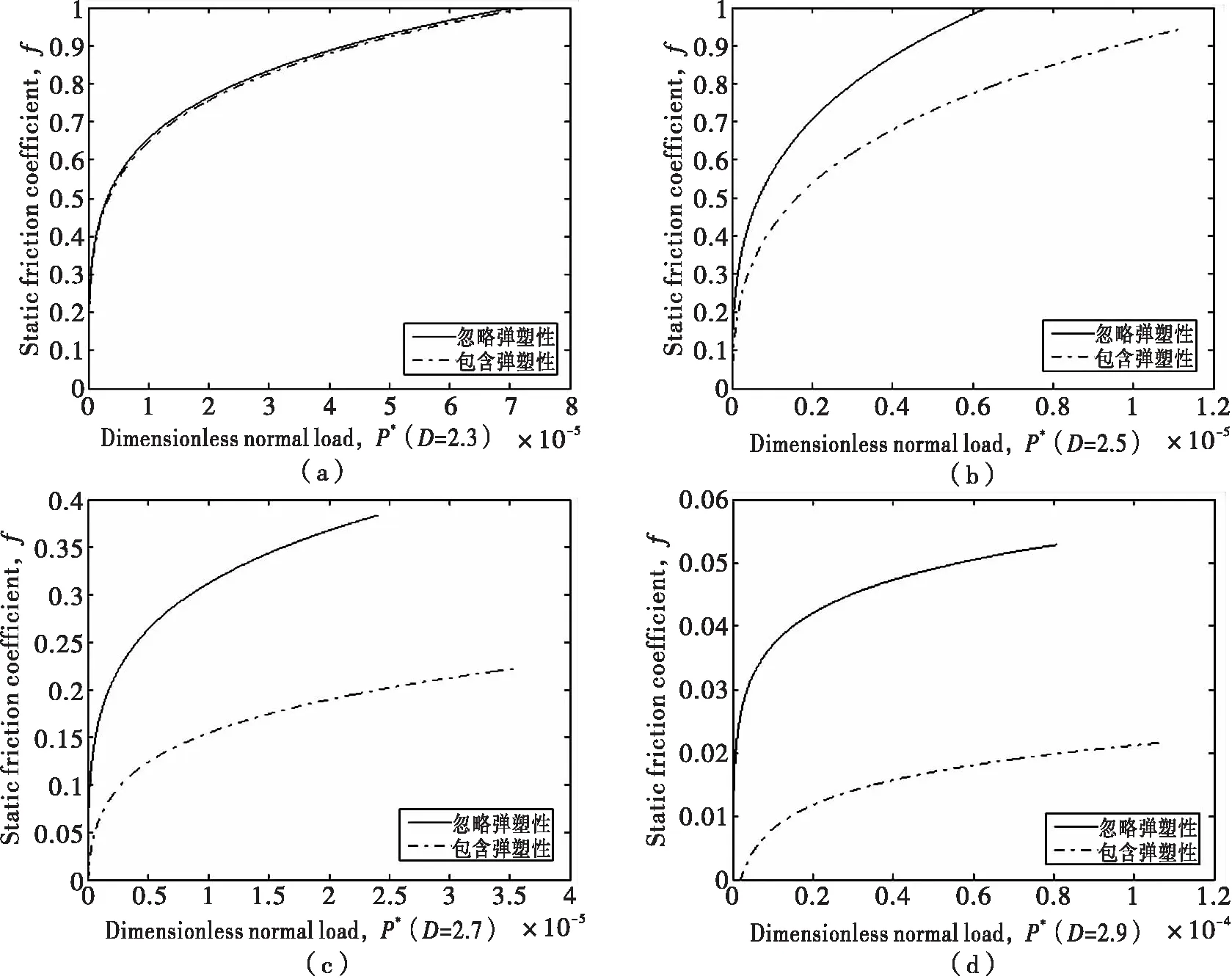
当2 (18) 当D=2.5时, (19) 根据接触点的实际接触面积a与其截面积a′之间的关系a′=2a,有: (20) (21) 将式(20)、式(21)带入式(18)、式(19)得:当2 (22) 当D=2.5时, (23) 将式(22)、式(23)无量纲化,得:当2 (24) 当D=2.5时, (25) 根据文献[6]可知,当微凸体的接触界面达到完全屈服时,结合面单个微凸体承受的切向载荷: 完全弹性区和弹-塑性一区的微凸体的接触面积和接触载荷分别为式(1)~式(4).因此完全弹性区和弹-塑性一区的微凸体的切向载荷分别为: 完全弹性区和弹-塑性一区的微凸体,在结合面处于临界滑动状态时,接触界面都将达到完全屈服,所以此时微凸体所受到的切向的总载荷Q就是最大静摩擦力[6]。 (26) (27) (28) 将式(20)、式(21)带入式(26)得: (29) 将式(27)、式(28)带入式(29)得:当2 (30) 当D=2.5时, (31) 将式(30)、式(31)无量纲化,得: 当2 (32) 当D=2.5时, (33) 图2 D对f的影响 静摩擦因数的计算公式为: (34) 将式(24)、式(25)、式(32)、式(33)带入式(34)得结合面静摩擦因数。 图3 P*对f的影响(K=2.8,φ=1.0,G*=1.0×10-5) 图4 G*对f的影响(K=2.8,φ=1.0) 图5 忽略与包含弹塑性过渡变形机制的两种模型仿真结果对比 由仿真结果可见 1)由图2可知,结合面静摩擦因数随着分形维数的增大,先增大再减小。 2)由图3可知,结合面静摩擦因数随着无量纲法向接触总载荷P*的增大而增大,并且呈凸弧非线性关系。 3)由图4可知,结合面静摩擦因数随着无量纲分形特征长度尺度参数G*的增大而减小。 文献[4]中的静摩擦因数三维分形模型与本文考虑弹-塑性变形机制的摩擦因数三维分形模型仿真结果对比如图5所示。由图5可以看出,忽略弹-塑性与包含弹-塑性模型仿真结果表明,静摩擦因数都是随着分形维数的增大,先增大然后减小;随着无量纲法向总载荷的增大而增大。两种模型的曲线走势接近,但由于考虑了弹-塑性变形机制,摩擦因数的值均小于忽略弹-塑性的摩擦因数的值。 (1)本文提出了一种基于三维分形理论,考虑弹-塑性过渡变形机制的结合面静摩擦因数三维分形模型,该模型可以用于进行结合面静摩擦因数的预测。 (2)结合面静摩擦因数随着分形维数的增大,先增大后减小;随着分形特征长度尺度参数的增大而减小;随着法向总接触载荷的增大而增大。 (3)考虑弹-塑性过渡变形机制的结合面静摩擦因数要小于不考虑弹-塑性变形机制的结合面静摩擦因数。 参考文献: [1] CHANG W R,ETSION I,BOGY D B.Static Friction Coefficient model for metallic rough surfaces[J].J Tribol ASME,1988,110(1):57-63. [2] GREENWOOD J A,WILLIAMSON J B P.Contact of nominally flat surfaces[J].Proceedings of The Royal Society of London,1966,A295:300-317. [3] YAN W,KOMVOPOULOS K.Contact analysis of elastic-plastic fractal surfaces[J].J Appl Phys,1998,84:3617-3624. [4] 殷东华,张学良,温淑花.结合面静摩擦因数三维分形模型[J].太原科技大学学报,2013,34(6):451-455. [5] LIOU J L.The Theoretical study for microcontact model with variable topography parameters[D].Tiwan:National Cheng Kung University,2006. [6] 尤晋闽,陈天宁.结合面静摩擦系数的统计模型[J].振动与冲击,2010,29(12):26-29. [7] 张学良.机械结合面动态特性及应用[M].北京:中国科技出版社,2002. [8] KOGUT L,ETSION I.A Static friction model for elastic-plastic contacting rough surfaces[J].ASME Journal of Tribology,2004,126(1):34-40. [9] KOGUT L,ETSION I.A semi-analytical solution for the sliding inception of a spherical contact [J].ASME Journal of Tribology,2003,125(3):499-506. [10] 兰国生,张学良,丁红钦,等.基于分形理论的结合面静摩擦因数改进模型[J].农业机械学报,2012,43(1):213-218.
2 考虑弹塑性变形的静摩擦因数三维分形模型
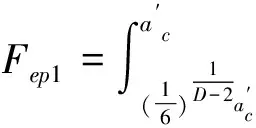
3 模型仿真
4 结论
