约束函数估值策略辅助的微粒群算法

高 鸽，孙超利，曾建潮(太原科技大学电子信息工程学院，太原 030024)

随着科学技术的不断发展，许多实际工程领域的最优化问题呈现出越来越复杂的特性，如目标函数、约束函数不能用解析式表达，而是通过复杂的仿真进行计算，需要花费大量的计算机时间。近年来，利用随机搜索算法求解约束优化问题得到了更多的重视。随机搜索算法对函数的性质要求非常低，可以用于一般的复杂工程优化问题。微粒群算法是随机搜索算法的一种，由于它不要求优化函数连续或可微，采用简单的速度位移进化模型，需调整的参数数量少，求得解的质量高、时间短，因此近年来得到了广泛的应用[1-4]，并取得了一定的成果。然而，作为群体算法，微粒群算法在获得最优解之前需要进行大量的适应值计算，而对于约束优化问题，若约束函数计算费时，则还需要耗费大量的约束函数计算时间，因此，微粒群算法不适合于求解计算费时的约束优化问题。

据了解已有较多的学者对适应值计算费时问题展开研究，如崔方舒等[5]将广义回归神经网络(GRNN)与PSO算法相结合，提出了适合求解随机优化问题的智能算法， 通过对预测策略及模型更新策略的分析决定个体的适应值是否用实际的适应值函数计算，节省了大量适应值计算时间；针对带约束的多目标优化问题，Hemant Kumar Singh等[6]人将代理模型应用到模拟退火算法中，提出了SASA算法，节省了实际函数的计算次数。Yao等[7]以支持向量机作为代理模型，提出分类辅助微分进化算法，用来判断哪一个后代个体的适应值需要用实际的适应值函数计算；Sun等[8]人根据同一代粒子之间的距离关系，提出了一种新的适应值预测模型，即某代任意粒子适应值已知，则该进化代中任意其他粒子的适应值就可以通过预测得到；Z.Cui等[9]提出了一种快速PSO算法，不需要计算所有粒子的适应值，只有当可信度低于某个阈值时，才需要实际计算该粒子的适应值；为了避免局部收敛，该作者又采用了一种新的策略，即被估计个体的适应值通过加权组合来确定，而每一个父代个体的权重是与周围被估计的粒子与它本身之间的距离成比例的[10]。

然而，对于约束函数计算费时问题研究的人并不多。大部分学者针对约束函数计算费时问题，都是通过罚函数法将其转换为无约束优化问题，然后进行求解。然而，罚因子的选取本身就是一个优化问题。Sasena等[11]意识到了上述问题，在有效的全局优化算法(EGO)背景下研究了约束处理问题，避免了在不可行域中采样，间接地减少了约束函数的计算次数，在本文中，我们称这种方法为保持约束可行法。C.K.Goh等[12]人提出了元模型协同进化算法来处理目标函数和约束函数计算费时问题，提高代理模型进化技术的效率。文献[13]首先使用罚函数来处理约束冲突，然后对罚函数应用代理模型，以解决罚函数选取难的问题，该方法使用一种连续的技术来更新模型，但是模型的质量缺理论准确性。文献[14]针对非线性约束优化问题为每个约束函数建立一个可以提高精度的模型，随着迭代搜索的进行，模型准确性逐渐提高，可行域会从一个简单的线性模型逐渐向原真实模型逼近，确保求得的最优解时原问题的最优解。

文献[15]提出一种新型向量微粒群算法，该算法定义了一个收缩系数确保个体任意维上都在约束边界内，同时定义了一个函数来判断粒子是否在可行域内，整个处理过程都为向量模式。S.He等[16]利用“回飞”策略，直接用上一代个体的位置来替代当前的不可行位置；Sun等分别使用一维搜索[17]和多维搜索[18]的方法为不可行个体在其飞行轨迹或其周围寻找一个可行位置以替代该不可行个体的位置，但是在找到一个可行位置之前可能需要很多次约束函数的计算，如果约束函数计算费时的话无疑是很消耗时间的，显然很不适用。本文拟将寻找一种简单有效的约束冲突判断方法，以替换实际的、费时的约束函数计算，减少整体优化时间，使得微粒群算法能够适合此类优化问题。

由于对于种群中的任何一个个体，均只有可行和不可行两种可能，因此，针对约束函数的判断，构造一个基于支持向量机分类器的预测微粒群算法，并与保持约束可行法和一维搜索方法的思想相结合，用于判断某一个体的可行性，来替换实际的约束函数计算，以解决约束函数计算费时问题的复杂优化问题。

1 基本概念

1.1 约束优化问题

约束优化问题的数学模型可以表示为：

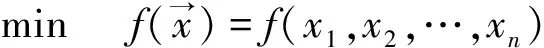
(1)

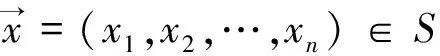
若一个变量在可行域内，则称该变量为该约束优化问题的一个可行解。

在本文中，将使用一下数学模型用于约束优化问题初始可行解的产生以及约束冲突的判断：

s.t.ximin≤xi≤ximax,i=1,2,…,n

(2)

其中，δ为容忍度，用于将等式约束转化为两个不等式约束来处理。

1.2 微粒群算法

1995年，Kennedy和Eberhart等通过对鸟群和鱼群群体捕食行为的模拟，提出了一种全局优化算法——微粒群算法(PSO)，实现了对优化问题的求解[19-22]，自微粒群算法提出以来，不断的有专家学者对其收敛性能进行修改以适应不同的应用，文献[23]简要回顾了微粒群算法的历史，并强调其飞行轨迹的随机稳定性的重要性。在该算法中，每一个微粒代表一个候选解，它在D维搜索空间中没有重量没有体积却具有一定飞行速度，并且能根据自身以及同伴的飞行经验动态地调整自己的飞行速度。

对于第i个微粒第t+1代的速度和位置，微粒群算法的进化公式可用公式(3)和(4)表示。

(3)

(4)

其中，ω为惯性权重，c1和c2分别为认知系数和社会加速权重，r1和r2为在[0，1]范围内均匀分布且相互独立的随机函数。

1.3 支持向量机原理

支持向量机是在统计学习理论和结构风险最小原理基础上发展而来的新的机器学习算法，从本质上看，它避开了从归纳到演绎的传统过程，实现了高效的从训练样本到预测样本的“转导推理”，大大简化了分类和回归等问题。其原理是利用非线性映射将数据集映射到高维空间，从而使得低维线性不可分的数据在高维空间线性可分。

SVM的目标是对特征空间划分最优超平面，支持向量是它的训练结果，在SVM分类决策中起决定作用的就是支持向量，而且只由少数的支持向量所决定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数。这不但可以帮助我们抓住关键样本、剔除大量冗余样本，而且注定了该方法具有较好的鲁棒性。这种鲁棒性主要体现在：增加或删除非支持向量对模型没有影响；支持向量样本集具有一定的鲁棒性。

在样本线性可分的情况下，将N个样本的训练集正确分类的判别函数形式为：y(x)=ωx+b.不仅能将两类样本正确分开，而且使得分类间隔最大的分类面就是最优分类面，最优分类面上的样本即为支持向量。

最优化问题最初的数学提法中目标函数实际上是一个严格的凸规划。按照最优化理论中凸二次规划的解法，通常把它转化为Wolfe对偶问题来求解。原最优化问题的Wolfe对偶问题，如式(5)所示。

(5)

式(5)的解即为原最优化问题的整体最优解。解出α后，即能确定最优超平面，得到其判别函数。

利用Wolfe对偶问题，不但能更好地处理问题，而且能使样本在新问题中仅以向量点积的形式出现看，正是这样一个重要特点，使支持向量机方法能推广到非线性情况。

对非线性问题，可以通过非线性变换转化为某个高维空间中的线性问题，在高维特征空间中求最优分类面。支持向量机采用的是满足Mercer条件的核函数k(xi,xj)=φ(xi)φ(xj)，将样本变换到高维空间。这时的目标函数和相应的分类函数分别为式(6)和式(7)所示。

(6)

(7)

最常用的核函数[24-25]有线性内积函数、多项式内积函数、 径向基内积函数[26]和Sigmoid核函数。

2 基于支持向量机分类方法的微粒群算法(SVMPSO)求解约束计算费时优化问题

文献[27]提出的基于一维搜索约束保持法的微粒群算法(ODCPVPSO)方法，对于每个个体位置都实际计算它的约束冲突值，如果满足约束条件则计算它的适应值，否则，使用一维搜索的方法寻找满足约束函数的新位置，寻找最佳步长因子β，最终使得H(xi(t)+β(xi(t+1)-xi(t)))=0，这样就为每个逃逸粒子产生了一个新的可行位置。

基于文献[27]的约束处理机制，利用样本构建一个支持向量机作为判断约束满足与否的分类器。加入SVM分类之后，先用SVM对每个粒子进行约束函数值分类，再对分类在可行域的粒子进行实际计算其约束冲突值，若实际也满足约束条件，再计算其适应值；否则，若用SVM估计个体不在可行域内，则对该逃逸个体使用一维搜索的方法优化约束冲突函数的时候，也采用同样的过程，具体的流程图如图1所示。

从图1中我们需要注意一点，构造支持向量机时为脱机训练，因此如何选择样本集，使得训练支持向量机时产生的最优超平面能更精确地将两类解分开是关键。

假设支持向量机训练样本个数为N，种群大小为n.

方案一：初始化产生N/2个粒子，将这N/2个粒子约束在不可行域内，作为不可行解部分，再产生N/2个粒子，将其约束在可行域内，作为可行解部分，二者共同构成支持向量机的训练样本。再从这N/2个可行解中选取n个作为种群初始化的粒子，进行后续进化过程。

由此看来，在将粒子约束在不可行域和可行域的过程中，至少要计算N次约束函数值，浪费了不少时间。于是本文采用另一种样本产生方法，方案如下。

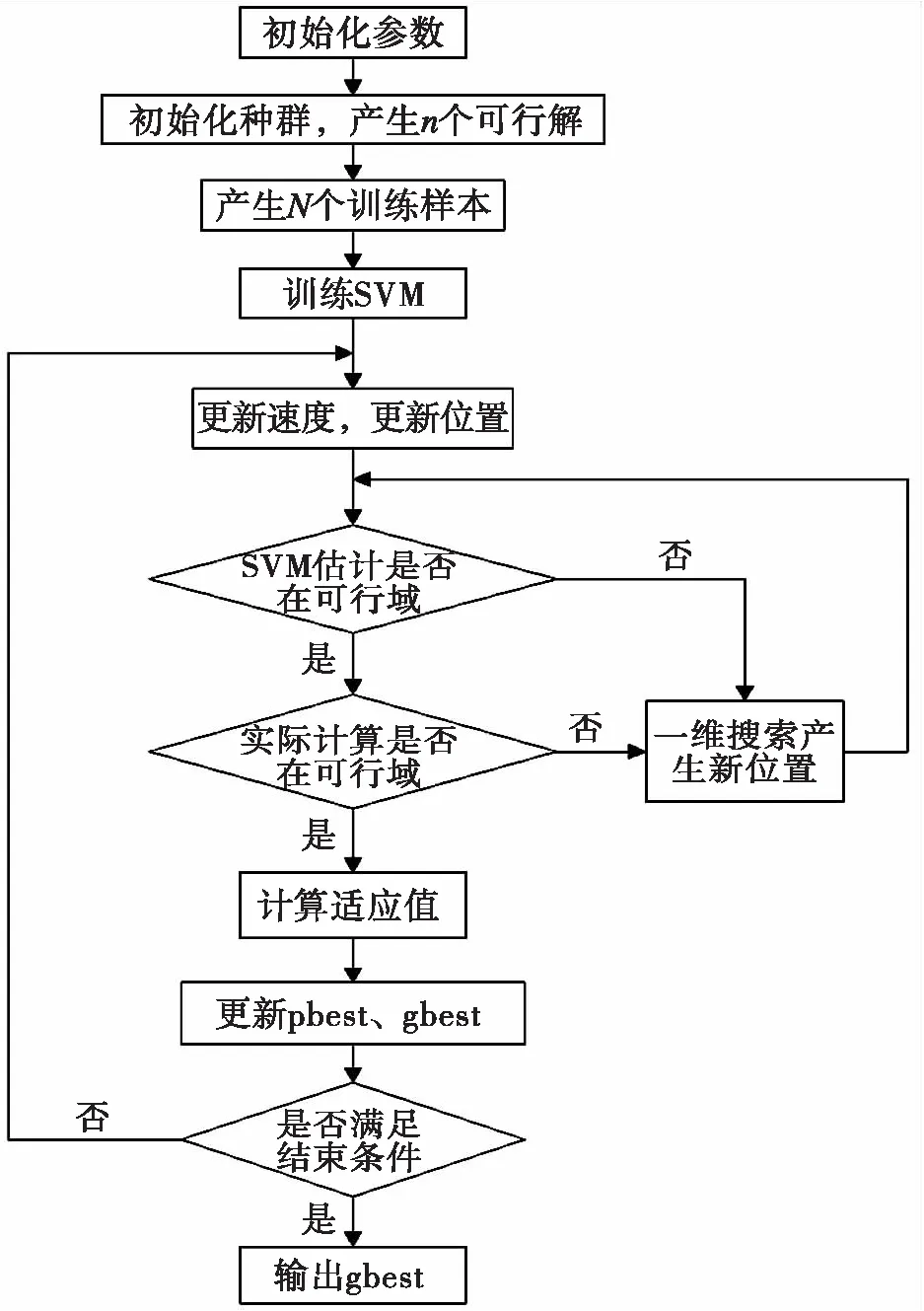
图1 SVMPSO算法解决约束优化问题流程图 Fig.1 The training strategy of SVM-assisted PSO

方案二：在初始化产生n个可行解基础上更新位置，对于每个粒子，计算其约束函数值，判断其是否满足约束冲突，若满足，则将其放入样本集的可行解库中，否则将其放入样本集的不可行解库中，同时采用一维搜索的方法，产生相应的可行解放入样本集的可行解库中。继续进化，进行同样的操作，直到产生N/2个不可行解为止。其流程图如图2所示。

无论是哪一种方法，支持向量机都是针对小样本数据处理问题的，而且问题描述的可行域所占整个搜索空间的比值[27]不同，所以在选择样本数N时，要视情况而定。

3 实验分析

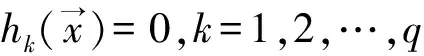
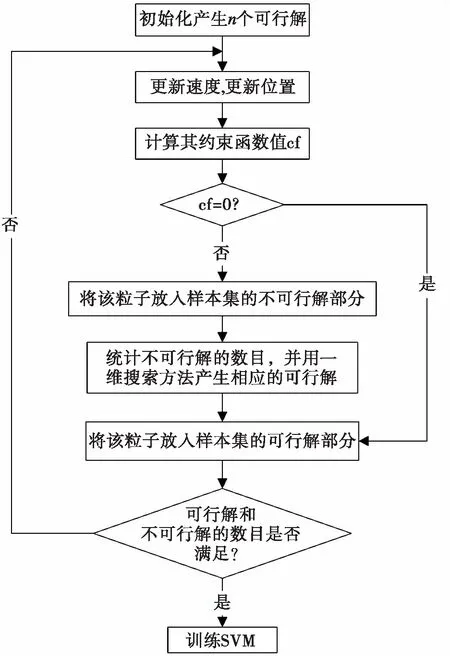
图2 样本产生方案二流程图

由式(5)解出的拉格朗日乘子α中，只有一部分对确定最优超平面起作用，本文选取这一部分的原则是：选择一个阈值，使大于等于这个阈值的α数为原α数的1/3到1/2之间，小于这个阈值的默认为0，不起作用，由这些起作用的α确定所需的支持向量。经过实验验证，设置阈值使大于等于这个阈值的α数为原α数的1/3到1/2之间相对于其它阈值所得的效果好。表1将仿真结果与ODCPVPSO算法的仿真结果进行比较。

为了评价SVMPSO算法的有效性，本文将SVM-PSO算法与ODCPVPSO算法中约束函数值的实际计算次数进行比较，比较结果见表2，其中ρ为SVMPSO算法比ODCPVPSO算法中约束函数值的实际计算次数减少的百分比。

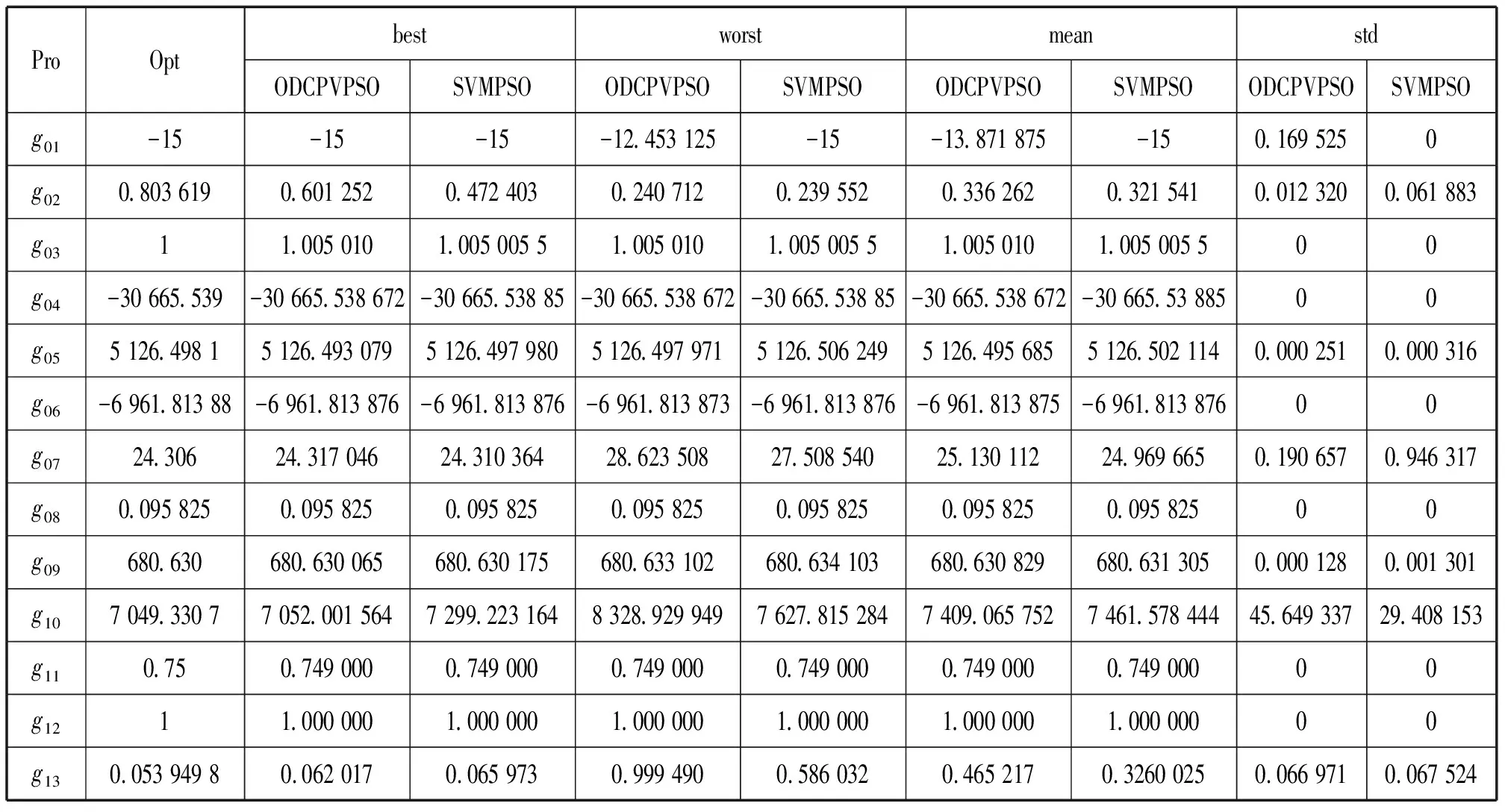
表1 SVMPSO算法与ODCPVPSO算法的优化结果比较

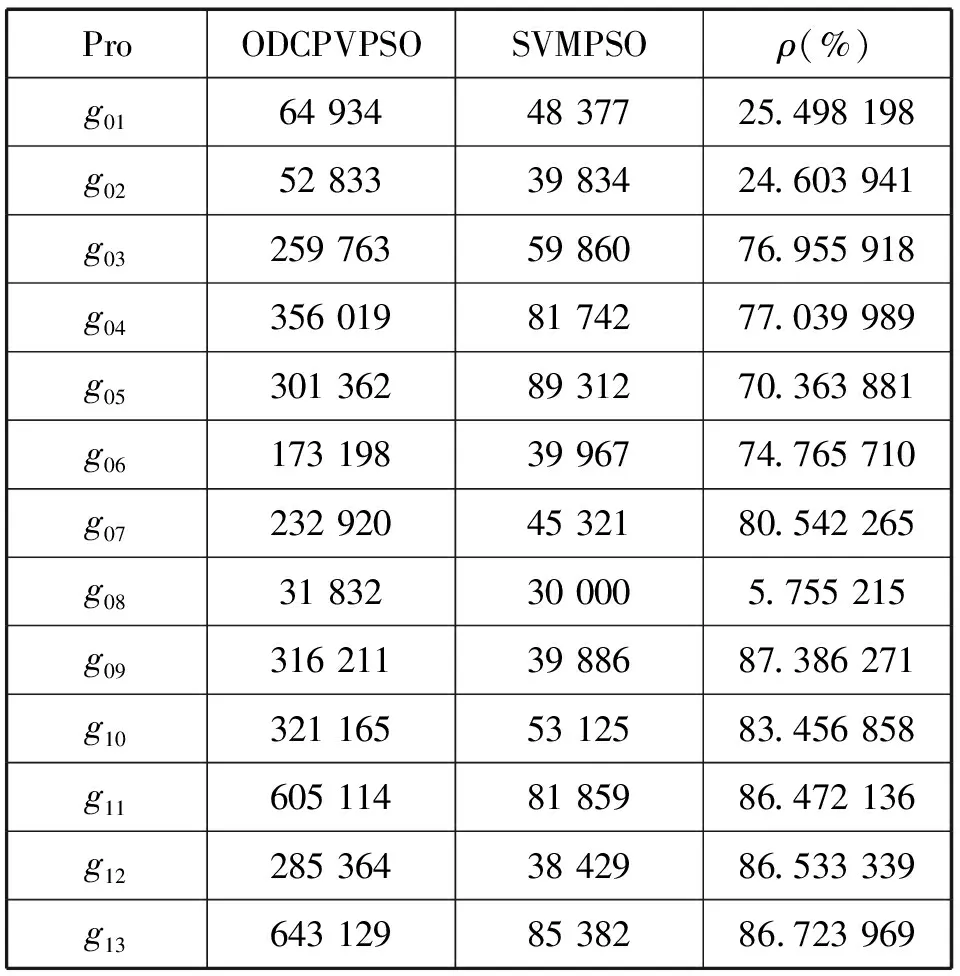
表2 SVMPSO算法与ODCPVPSO算法中约束函数值的实际计算次数比较结果

从表1整体上可以看出，SVMPSO算法所求出的最优解与最差解比偏差不大，较为平稳。除了g02和g10之外，SVMPSO均取得了与ODCPVPSO相同或者更好的最优解。

从表2可以看出，SVMPSO算法大大减少了约束函数值的实际计算次数。

4 总结

本文通过构建支持向量机分类器来判断PSO算法中的个体是否满足约束冲突条件，避免复杂的约束计算，缩短了整体优化时间。通过最优解和约数函数实际计算次数的比较结果表明SVMPSO算法既保持了算法的性能，同时又大幅度减少了约束函数的计算量，从而节省大量时间，达到预期效果。本文算法采用脱机训练的方式构建支持向量机，然而，这种方式会受到样本数量、样本选择等的限制，由于在微粒群算法进化过程中，会产生大量实际计算的约束函数值信息，因此，如何利用进化过程中的这些信息，用于更好、更准确的构建分类器，将是我们今后的研究方向。

参考文献：

[1] MOHAMMAD SALEHI MALEH，SOODABEH SOLEYMANI，RAMTIN RASOULI NEZHAD，et al.Using Particle Swarm Optimization Algorithm Based on Multi-Objective Function in Reconfigured System for Optimal Placement of Distributed Generation[J].Journal of Bioinformatics and Intelligent Control，2013，2(2)：119-124.

[2] DERRAR H，AHMED-NACER M，BOUSSAID O.Particle swarm optimisation for data warehouse logical design[J].International Journal of Bio-inspired Computation，2012，4(4)：249-257.

[3] ALI L，SABAT S L，UDGATA S K.Particle swarm optimisation with stochastic ranking for constrained numerical and engineering benchmark problems[J].International Journal of Bio-inspired Computation，2012，4(3)：155-166.

[4] ABDELSALAM H M，MOHAMED A M.Optimal sequencing of design projects′activities using discrete particle swarm optimisation[J].International Journal of Bio-inspired Computation，2012，4(2)：100-110.

[5] 崔方舒，适合于随机优化问题的微粒群算法的研究[D].太原：太原科技大学，2009.

[6] SINGH H K，RAY T，SMITH W.Surrogate Assisted Simulated Annealing(SASA)for Constrained Multi-objective Optimization[C]∥Evolutionary Computation (CEC)，IEEE，2010：1-8.

[7] LU X，TANG K，YAO X.Classification-assisted differential evolution for computationally expensive problems[C]∥Evolutionary Computation (CEC)，IEEE，2011：1986-1993.

[8] SUN C L，ZENG J C，XUE S D，et al.A new fitness estimation strategy for particle swarm optimization[J].Information Sciences，2013，181：355-370.

[9] CUI Z H，ZENG J C，SUN G.A fast particles swarm optimization[J].International Journal of Innovative Computing，Information and Control，2006，2：1365-1380.

[10] CUI Z H，CAI X J，SHI Z Z.Using Fitness Landscape to Improve the Performance of Particle Swarm Optimization[J].Journal of Computational and Theoretical Nanoscience，2012，9(2)：258-266.

[11] SASENA M J，PAPALAMBROS P，GOOVAERTS P.Exploration of Metamodeling Sampling Criteria for Constrained Global Optimization[J].Engineering Optimization，2002，34：263-278.

[12] GOH C K，LIM D.A surrogate-assisted memetic co-evolutionary algorithm for expensive constrained optimization problems[C]∥ Evolutionary Computation (CEC)， IEEE，2011：744-749.

[13] RUNARSSON T P.Constrained evolutionary optimization by approximate ranking and surrogate models [C]∥ Parallel Problem Solving from Nature-PPSN Ⅷ，2004：401-410.

[14] JIN Y，OH S，JEON M.Incremental approximation of nonlinear constraint functions for evolutionary constrained optimization[C]∥Evolutionary Computation (CEC)，IEEE，2010：1-8.

[15] SUN C L，ZENG J C，PAN J S.A New Vector Particle Swarm Optimization for Constrained Optimization Problems[C]∥International Joint Conference on Computational Sciences and Optimization， 2009：485-488.

[16] HE S，PREMPAIN E，WU Q H.An improved particle swarm optimizer for mechanical design optimization problems[J].Engineering Optimization，2004，36：585-605.

[17] SUN C L，ZENG J C，PAN J S.A New Vector Particle Swarm Optimization for Constrained Optimization Problems[C]∥Computational Sciences and Optimization，2009：485-488.

[18] SUN C L，ZENG J C，PAN J S.An improved vector particle swarm optimization for constrained optimization problems[J].Information Sciences，2011，181：1153-1163.

[19] JIANG M S.Analysis in particle swarm optimization[C]∥swarm intelligence symposium，2007：92-99.

[20] YE G Q，SUN S Y.Particle swarm optimization based on dynamic population size [J].Information and Control，2008，37：18-27.

[21] LIU H B，WANG X K，TAN G J.Convergence analysis of particle swarm optimization and improvement of chaotic[J].Control and Decision，2006，21：636-640.

[22] GUANG Q L，ZHAO F Q.Parallel hybrid PSO-GA algorithm and its application to layout design[J].Structural and Multidisciplinary Optimization，2006，33：749-758.

[24] 李海生，支持向量机回归算法与应用研究[D].广州：华南理工大学，2005.

[25] 祝红梅，支持向量机核参数选择及其应用[D].西安：西安科技大学，2007.

[26] FATTAHI H，FARSANGI M A E，SHOJAEE S，et al.Application of the hybrid harmony search with support vector machine for identification and classification of damaged zone around underground spaces[J].International journal of optimization in civil engineering，2013，3：345-358.

[27] 孙超利，面向机械化设计的微粒群算法理论及其应用研究[D].太原：太原科技大学，2010.

[28] THOMAS P R，XIN Y.Stochastic Ranking for Constrained Evolutionary Optimization[J].Evolutionary computation，2000，4：284-294.