无限大压电材料薄板Ⅰ型裂纹断裂分析
2014-06-13解海玲张雪霞赵文彬余路娟太原科技大学太原030024
解海玲,张雪霞,赵文彬,余路娟(太原科技大学,太原 030024)
压电材料在发生机械变形时产生电场,当受到电场作用时发生机械变形,因其具有这种独特的机电耦合性质,被广泛用于制作高精度传感器、制动器、高精度位移器等电子器件中,还应用于精密仪器、航天航空、自动控制等领域。因此,随着这种具有智能特性的压电材料的快速发展,压电材料已成为现代工程材料的一个重要的分支。压电材料作为智能结构器件的核心材料,其力电耦合静动力特性的研究得到了普遍的重视。但是压电材料自身有很大的脆性,在制造和使用过程中不可避免地出现缺陷(如裂纹、夹杂、孔洞等),往往会导致材料过早地失效或者发生破坏,从而影响智能结构的性能和可靠性,因此研究压电材料的断裂问题有十分重要的意义。
Parton[1]从线性压电本构关系出发,研究了远场作用机械载荷时压电介质中的有限长裂纹的平面应变问题,得到了广义的Griffith能量释放率。胡克强[2]基于线性压电理论,采用电绝缘边界条件,对压电板条中的张开型(Ⅰ型)裂纹问题进行了求解,得到了裂纹尖端场的强度因子。Sosa[3]分析了一个含有缺陷的二维横观各向同性压电体,求出了在不可导通边界条件下无限大压电平面含有椭圆孔口时的平面电弹性问题的精确解析解。Yang[4]采用可导通边界条件给出了无限大压电介质中Ⅰ型裂纹问题的封闭解。李尧臣[5]在压电材料平面问题复变函数形式的通解的基础上,推导了裂纹问题的应力强度因子和电位移强度因子的一般表达式。郭俊宏[6]研究了含周期性裂纹正交各向异性板平面问题,对平面问题的应力场进行了分析。陈梦成[7]讨论了不可导通情况下三维横观各向同性压电材料中受拉伸和电载荷作用的平片裂纹Ⅰ型断裂力学问题,得到了以裂纹面位移间断和电势间断表示的应力和电位移强度因子、能量释放率表达式。Gao[8]用复势的方法研究了含椭圆形孔的压电材料受到远场均匀载荷的二维问题,得到满足电边界条件的椭圆孔内、外的封闭解和当椭圆孔变为裂纹时的应力强度因子。杨丽敏[9]利用Lekhnitskii理论和Stroh理论的相互联系,把已知的基于Lekhnitskii理论平面应变结果转化为Stroh理论形式的结果,导出压电材料平面应变问题的尖端场Williams形式的展开式,采用半权函数法计算有限大压电体平面问题应力和电位移强度因子。刘新民[10]用复变函数的方法,研究了压电材料平面可导通裂纹的机电耦合场及其奇异性。赵文彬[11]在弯扭载荷作用下,利用复变函数方法研究线弹性各向异性纤维复合材料板裂纹尖端附近的应力场、位移场,并且推出裂纹尖端附近的应力和位移计算公式。冯中华[12]等人利用复变函数方法,半逆解法及待定系数法,研究了压电材料的共线周期性裂纹问题,给出了在电不可导通边界条件下的应力、电位移、应力强度因子、电位移强度因子和机械应变能释放率的解析解。
近年来,研究压电材料断裂问题的文献很多,所用的方法也很多。但是用复变函数方法和待定系数法来研究压电材料断裂问题的文献还很少,此方法比已有文献中所用的方法简单,而且能有效地解决压电材料的一类问题。
本文研究了在无穷远处平面应力和电位移共同作用下,含中心裂纹的无限大横观各向同性压电材料薄板的平面问题。运用复变函数方法和待定系数法,选取适当的应力函数,得到在不可导通边界条件下裂纹尖端附近的应力强度因子、应力场、电位移场和位移场、电势场的计算公式。
1 压电材料薄板的控制方程
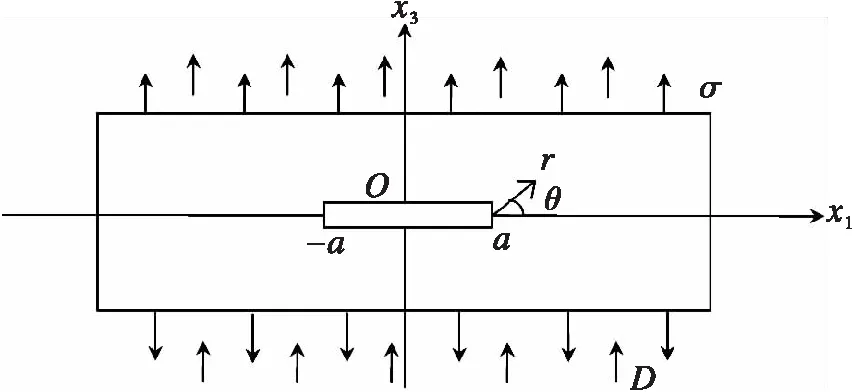
图1 含中心裂纹的无限大压电材料薄板
考虑一个含有长为2a的中心裂纹的无限大横观各向同性压电材料薄板,在无穷远处受到平面应力σ和平面内电位移D共同作用。如图1所示。
本文考虑的是横观各向同性压电材料薄板,缺陷位于x1ox3平面,极化方向沿着x3轴的方向,在忽略体力和自由电荷的情况下,对应的平面问题的基本方程如下:
本构方程:εij=sijklσkl+gkijDk,Ei=-giklσkl+βikDk
(1)
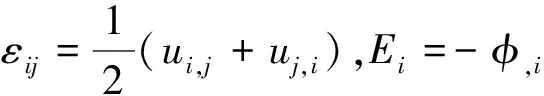
(2)
其中σij为应力;Di为电位移;εij为应变;ui为位移;Ei为电场强度;φ为电势;sijkl、gkij、βik分别为弹性常数、压电常数、介电常数;i,j,k=1,2,3,式(2)中ui,j、uj,i、φ,i中小标中的逗号表示求偏导。
在平面应变问题下,假设ε22=ε32=ε12=E2=0[8],
(3)
将式(3)代入式(1)中得到平面应变问题下的本构方程:
ε11=a11σ11+a12σ33+b21D3;
(4)
ε33=a12σ11+a22σ33+b22D3;
(5)
2ε31=a33σ31+b13D1;
(6)
E1=-b13σ31+δ11D1;
(7)
E3=-b21σ11-b22σ33+δ22D3.
(8)

(9)
(10)
分别由式(9)、式(10)消去u1,u3和φ得到如下方程:
(11)
引入函数U=U(x1,x3)和Φ=Φ(x1,x3),则:
(12)
由式(4)-式(8)及式(11)-式(12),可得如下偏微分方程组:
(13)
利用式(13),消去Φ(x1,x3)得:
(14)
这是一个六阶常系数齐次线性偏微分方程,对于图1所示的Ⅰ型裂纹,采用不可导通的边界条件,即认为在裂纹面处电位移为0.边界条件[2]如下:
x3→∞∶σ33=σ,D3=D,σ31=0
(15)
x3=0,|x1| (16) 假设应力函数: U(z)=U(x1+sx3) (17) 将式(17)代入到式(14)中得到特征方程: a11δ11s6+(a11δ22+2a12δ11+a33δ11+b132+2b13b21+b212)s4+ (18) (19) 其中α2,β1,β2均为实常数。 (20) (21) 其中Uj应力函数: (22) 将式(20)-式(22)代入到式(12),得到应力场和电位移场: (23) (24) (25) (26) (27) (28) (29) 当x3→∞时,Uj=σ (30) 将式(22)-式(27)、式(29)、式(30)代入到式(15)、式(16)得到如下方程组: (31) 解方程组式(31)得: (32) (33) (34) (35) (36) (37) (38) 将Zj=x1+sjx3及式(38)代入到式(26),则在裂纹尖端附近有: (39) 由式(17)、式(21)-式(25)式及式(39)得应力场和电位移场: (40) (41) (42) (43) (44) 将式(40)-式(44)代入到式(4)、式(5)、式(7)得应变ε11、ε33和电场强度E1如下: (45) (46) (47) 由式(45)-式(47)积分得位移场和电势场的计算公式如下: (48) (49) (50) 运用复变函数方法和待定系数法,研究了含中心裂纹的无限大横观各向同性压电材料薄板在无穷远处受平面应力和电位移共同作用下的问题,得到不可导通边界条件下Ⅰ型裂纹尖端附近场问题的解。可得如下结论: 1)得到不可导通边界条件下Ⅰ型裂纹尖端附近的应力强度因子; 2)得到不可导通边界条件下Ⅰ型裂纹尖端附近应力场、电位移场、位移场和电势场的表达式,并从表达式可以看出,它们均可以由应力强度因子表示。 参考文献: [1] PARTON V Z.Fracture mechanics of piezoelectric materials[J].Acta Astronautics,1976(3):671-683. [2] 胡克强,李国强,仲政.压电板条中的平面裂纹问题[J].同济大学学报,2005,33(7):890-894. [3] SOSA H A.Plane problems in piezoelectric media with defects[J].International Journal of Solids and Structures,1991,28(4):491-505. [4] FUQIAN Y.Fracture mechanics for a modeⅠcrack in piezoelectric material[J].Int J Solids & Structs,2001,38:3813-3830. [5] 李尧臣.压电材料平面裂纹问题的强度因子和能量释放率[J].同济大学学报:自然科学版,2002,30(4):437-445. [6] 郭俊宏,卢子兴.含周期性裂纹正交各向异性板平面问题的应力场分析[J].复合材料学报,2010,27(1):162-166. [7] 陈梦成,张安哥,野田尚昭.压电材料中三维Ⅰ型断裂力学分析[J].力学学报,2005,37(1):15-25. [8] GAO C F,FAN W X.Exact solutions for the plane problem in piezoelectric materials with an elliptic or a crack[J].International Journal of Solids and Structures,1999,36(17):2527-2540. [9] 杨丽敏,柳春图,曾晓辉.压电材料平面问题的尖端场和应力强度因子的求解[J].应用力学学报,2005,22(2):212-216. [10] 刘新民.压电材料平面渗透裂纹的机电耦合场[J].中国机械工程,2001,12(S1):1-3. [11] 赵文彬,张雪霞.含裂纹各向异性复合材料板的断裂分析[J].太原科技大学学报,2011,32(1):67-71. [12] 冯中华,刘官厅.压电复合材料的共线周期性裂纹平面问题的电弹性场分析[J].复合材料学报,2012,29(2):199-204. [13] 杨维阳,李俊林,张雪霞.复合材料断裂复变方法[M].北京:科学出版社,2005.
(a22δ11+2a12δ22+a33δ22+2b22b21+2b22b13)s2+(a22δ22+b222)=0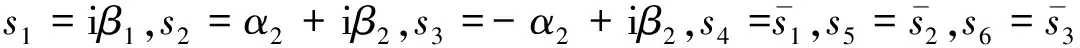
2 待定系数法
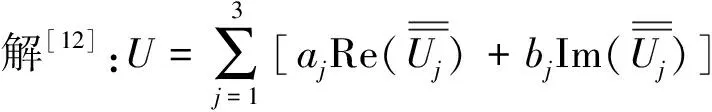



3 压电材料裂纹尖端的应力场和位移场
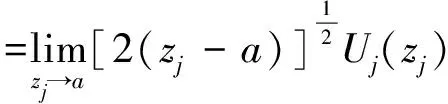

4 结论
