一种多组分分离级联的数值计算方法

丛艺坤

(核工业理化工程研究院，天津 300180)

稳定同位素被广泛应用于基础科学、地质学、生物学、医疗诊断以及半导体技术等领域。元素周期表中稳定的化学元素有83种，其中39种含有3种以上同位素组分，这类元素被称为多组分同位素元素。已有许多关于多组分同位素分离的理论和实验研究[1-7]。

离心法分离稳定同位素通常在各级流量相等的矩形级联中进行。研究多组分矩形级联的分离特性，必须求解描述级联内部物质输运规律的级联方程。由于多组分矩形级联方程是复杂的非线性方程组，只能用数值方法来求解，因此快速、稳定、精确地求解级联方程的数值计算方法是级联设计和优化的必要工具。关于多组分矩形级联方程求解的计算方法，在许多文献中进行了探讨，其中准线性法[8-9]、q迭代法[10-11]以及非稳态法[12-13]比较快速、稳定。

本研究将提供一种基于迭代序列差的能稳定收敛的多组分矩形级联的数值计算方法，并研究其准确性、稳定性和收敛特性。

1 级联数学模型

1.1 级联结构

本研究的级联模型为各级流量相等的逆流型矩形级联,结构示意图示于图1。级联总级数为n，供料级为f，各级供料流量为G。级联供、精、贫流量及第i组分的丰度分别用F、P、W，CFi，CWi，表示。F、P、W三个参量之间存在守恒关系，给定其中两个量，第三个量能唯一确定。

图1 逆流型矩形级联示意图Fig.1 Countercurrent square cascade

1.2 级的守恒及分离方程

假设第i组分在级联第s级的供料、精料和贫料流中的丰度分别为Cfi,s、Cpi,s、Cwi,s，第s级的分流比为θs，根据级联分离理论，存在以下组分物质守恒方程

θsCpi,s+(1-θs)Cwi,s，i=1，……，m

(1)

m为同位素混合物的组分数。

第s级的分离方程可表示为

(2)

γij为第i组分对第j组分的相对全分离系数。在通常情况下，相对全分离系数随级的供料丰度和分流比的变化而改变，但是对于大部分基于分子动力学的分离方法，相对全分离系数不随上述参量变化，并可表示为

γij=γ0Mj-Mi

(3)

γ0为基本分离系数，Mi为第i组分的摩尔质量。

另外，各组分丰度之和满足归一化条件，即

∑Cpi,s=1，i=1，……，m

(4)

对级联任意s级，在Cpi,s、γ0、Mi、θs已知的条件下，要求解Cpi,s、Cwi,s，存在m个守恒方程(1)(因为i=1，……，m)，m-1个分离方程(2)(因为在i=j时，γij=1，没有分离效应)，1个丰度归一化方程(4)，共2m个方程。作为未知量，有m个Cpi,s和m个Cwi,s，即共2m个未知量。因此利用方程(1)～(4)可求出Cpi,s和Cwi,s。

以消去Cwi,s为目的，把方程(1)代入(2)，化简可得

Cfj,s·Cpi,s-γijCfi,s·Cpi,s+θs(γij-1)·Cpi,s·Cpj,s=0，i=1，……，m，j=1，……，m

(5)

由(5)式求出Cpi,s之后，再利用(1)式可求出Cwi,s。

1.3 级的分流比及供料丰度的确定

要求解非线性方程组(5)，必须知道级联各级的分流比和供料丰度，各级分流比由具体的分离任务和分离工艺确定，一般是给定某一级的分流比(比如级联精料级分流比θn)，其他各级的分流比θs由第s级到级联端部间的物质守恒方程求出，即

在级联贫化段

(6)

在级联浓缩段

(7)

供料丰度Cfi,s实际上表示的是级联中各组分的丰度分布，其分布与级联的结构和管道连接方式密切相关。对如图1所示的逆流型矩形级联，Cfi,s可表示为

(8)

对于不同的级联形式，级间的丰度混合条件不同，(8)式也将随之改变。

2 计算方法

2.1 算法的基本思想

在Cfi,s、γij、θs已知的情况下，方程(5)是以Cpi,s为变量的非线性方程组，无法得到其解析解，只能通过数值方法求解。下面将具体介绍非线性方程组(5)的求解方法。由于各级的非线性方程组的求解过程完全相同，与s无关，因此，下面对方程组(5)的求解过程的阐述，将隐去角标s，即Cpi,s直接用Cpi表示。

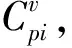
(9)

也就是说，下一次的迭代值可由本次迭代值加上相邻两次迭代的差值(迭代序列差)来求得，将(9)式代入(5)式中得

(10)

而将(9)式代入方程(4)中可得

(11)

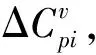
2.2 算法的收敛判据

收敛判据是指迭代计算停止的条件。不同的计算方法，其收敛判据也不同，有的以级联组分守恒方程为收敛判据，有的以精、贫料组分丰度的归一化条件为收敛判据。本方法所采用的收敛判据为级联组分守恒方程，即定义迭代误差为

(12)

当δ达到给定精度时，迭代停止，所得到的解为最终解。

2.3 算法的迭代步骤

算法的迭代步骤如下：

1) 根据(6)～(7)计算各级分流比θs。

3) 根据(8)式计算各级供料丰度Cfi。

4) 根据(9)～(11)式求新的Cpi，Cwi。

5) 验证精度δ是否达到给定值，如果达到，计算结束，否则，利用所得到的Cpi和Cwi，从第3步重新迭代。

2.4 算法的优越性

从以上对算法的阐述可知，本算法不同于传统的级联算法，传统的级联算法一般是在级联各级与级联端部之间建立起组分物质输运方程，且输运方程中包含分离方程所引起的非线性项，因此各算法的基本任务就是设法求解这些非线性的组分物质输运方程。如果级联的形式比较复杂，就会增加非线性方程组的求解难度。而本方法的核心就是针对迭代序列差求解各级的分离方程，而各级丰度混合条件即级间管道的连接方式只作为求解各级分离方程的约束条件，所以级联形式上的变化不会使分离方程的求解复杂化。因此本算法可以很方便地推广到带附加流级联、层架级联、非对称级联等复杂级联的计算。

本算法与非稳态法[12]有些类似，其求解过程就是中间解向最终解动态靠近的过程。需要指出的是，本算法为迭代算法，在求解过程中级联内部组分丰度的变化与时间不相关，与非稳态法有着本质的区别。

3 算法的特性研究

3.1 算法的准确性及其计算能力

根据上述算法，用Matlab软件编写了计算程序，由三个子程序组成，一个计算分流比，另一个计算由(8)式所确定的各级供料丰度，第3个用来求解级的分离方程。由于求解级的分离方程的子程序适用于所有形式的级联，因此，在级联形式改变的情况下，只需对前两个子程序进行相应的修改，方便计算。利用所编写的计算程序，进行了级联数值计算，并对与级联算法相关的一些特性进行了研究。

检验计算方法的准确性，可以通过两种途径，一是与实际级联的分离结果进行比较；二是由不同的计算方法得到的计算结果之间的相互验证。由于实际级联的联运行条件很复杂，不完全符合理论计算的假设条件。在理论研究阶段，用不同计算方法相互比较来检验理论计算结果的准确性是可行的。

为了验证本算法的准确性，对多遍分离硅-28级联进行了计算，采用的级联参数为：级联总级数n= 30级，供料级f=15级，基本分离系数γ0=1.2，级联分流比θc=0.6，供料流量与级间流量比为F/G=0.2，分离遍数为4遍。分离工质为SiHCl3，其组分的摩尔质量M和相应的天然丰度CFi列于表1。

表1 三氯氢硅(SiHCl3)各组分的摩尔质量及天然丰度

计算结果列于表2。四遍分离三氯氢硅，由于上一遍的精料将作为下一遍的供料，第一遍的精料丰度之和不满足归一化条件，误差将传递给下一遍的级联计算，并在每一遍分离计算中得到放大。到第四遍时，累积误差可能超过分离工艺所能允许的范围。在这种情况下，要求计算方法有比较高的精度，才能在多遍分离级联计算之后，满足实际分离工艺的精度要求。

表2 分离三氯氢硅(SiHCl3)的计算结果

从表2可见，本方法与准线性法计算所得到的结果完全一致。用文献[12]中提到的第二种计算方法，即非稳态法计算上述两种级联时，计算结果一致。通过上面的级联计算以及不同计算方法所得到的结果之间的比较，验证了本计算方法的准确性。

检验多组分分离级联计算能力的另一种情况是分离工质同位素组分多、级联长、级联分流比很小或接近全回流。虽然在实际分离工艺中很少有这种级联，理论上，用这种级联来检验一种计算方法的计算能力是完全合理的。为此，本研究以SiHCl3同位素分离为例进行了级联计算。级联总级数n= 50级，供料级f=10，基本全分离系数γ0=1.2。目标组分为最轻的组分。不同级联分流比θc和不同F/G值下的目标S组分的精料丰度CP1结果示于图2。

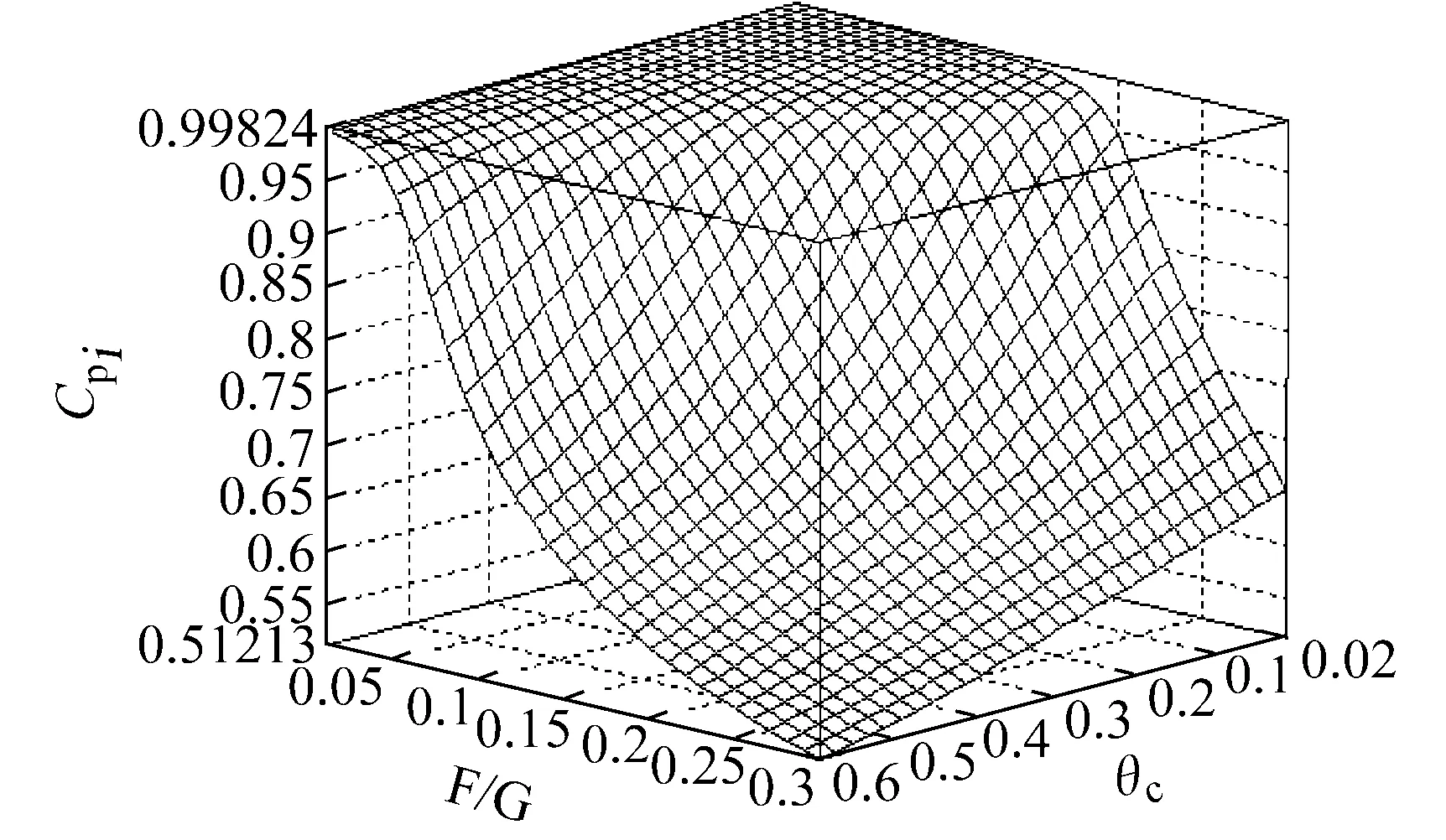
图2 目标组分的精料丰度CP1与θc和F/G之间的关系Fig.2 Relation of CP1, θc and F/G

从图2可以看出，当级联分流比θc从0.6减小到0.02，F/G从0.3减小到0.01时，目标组分丰度CPi平稳地增加到99.824%，表示目标组分丰度值的整个曲面没有突变(曲面局部严重向上凸起或向下凹陷)。结果表明，本算法在上述级联参数下都能稳定地收敛。尤其是当θc=0.02、F/G=0.01这种接近全回流情况下能稳定收敛，进一步说明本计算方法具有很好的稳定性和在组分很多、级联很长、级联分流比很小等极限情况下的计算能力。

3.2 算法的收敛特性

不同的算法有不同的收敛特性，有的算法对初始丰度依赖性比较强，当初始丰度与最终解比较接近时，算法能稳定收敛，而当初始值偏离最终解比较远时，算法不能收敛。有的算法在计算短级联时，能稳定收敛，而当计算多组分的长级联时，不能稳定收敛，或者只能收敛到一定精度。下面将以分离三氯氢硅为例，从三个方面来研究本算法的收敛特性，即收敛性与初始丰度的关系，收敛性与级联长度的关系以及收敛性与基本全分离系数的关系。

在研究收敛特性与初始丰度的关系时，级联总级数n= 30级，供料级f=6，基本全分离系数γ0=1.2，级联分流比θ=0.6，供料流量与级间流量比为F/G=0.2。选择三组不同的初始丰度，第一组是假设第一个组分的丰度为1，其余组分的丰度都为0，第二组为各组分丰度相等，第三组为表1所示的三氯氢硅的天然丰度。三种初始丰度下的迭代精度的对数lgδ与迭代次数V的变化关系示于图3。

图3 不同初值下迭代精度对数与迭代次数的关系Fig.3 Relation of accuracy and iterative times for different initial values

从图3可以看出，本算法最终都能稳定收敛到10～14量级以上。不同的初值只对收敛速度产生一定的影响，比如本算法收敛到10-13时，三种初值下的迭代次数分别约为6 000、6 100和7 000次(见图3)。为了比较各初值与最终结果的近似度，计算了初值与最终结果的协方差。第一、二、三组初值与最终解的协方差分别为12.531、4.537 6、0.526 18。三种初值下最终解的精度几乎一致。所以，认为初值对最终解的精度没有影响，只影响收敛速度，收敛速度由初值与最终解的近似程度决定的。最终解的各级供料丰度与天然丰度具有最高的近似度，把其作为迭代初始值时，算法收敛速度最快。

在研究算法收敛性与级联长度的关系时，初始丰度值取表1所示的三氯氢硅的天然丰度。基本全分离系数γ0=1.2，级联分流比θc=0.6，供料流量与级间流量比为F/G=0.2。供料级为第6级，不同级联总级数下迭代精度的对数lgδ与迭代次数的变化关系如图4所示。图4中的曲线分别表示级联总级数n=20、30、40、50下的收敛趋势。

图4中不同级联长度下的收敛趋势说明，级联长度对最终的收敛精度不产生影响，也就是说，无论是在哪种级联长度下，算法都能稳定地收敛到10-14量级以上。但是级联长度对算法的收敛速度影响很大。比如收敛到近10-14时，级联长度为20、30、40、50级所对应的收敛次数依次约为3 000、7 000、12 000、15 000次。

为研究算法收敛性与基本全分离系数的关系，初始丰度值取表1所示的三氯氢硅的天然丰度。计算时选用的级联总级数n=30级，供料级为f=6级，级联分流比θc=0.6，供料流量与级间流量比为F/G=0.2。不同基本全分离系数下迭代精度的对数lgδ与迭代次数的变化关系示于图5。图5中的曲线分别表示基本全分离系数γ0=1.1、1.2、1.3、1.4下的收敛趋势。

图5 不同基本全分离系数下迭代精度对数与迭代次数的关系Fig.5 Relation of accuracy and iterative times for different separation factor

图5中不同基本全分离系数下的收敛趋势说明，基本分离系数γ0对最终的收敛精度也不产生影响，无论是在哪种基本全分离系数下，算法都能稳定地收敛到10-14量级以上。同时对收敛速度有一定的影响，但其影响程度远没有级联长度对收敛速度的影响大。

从以上算例分析可以看出，本算法最终的收敛精度不依赖于初始丰度，不受级联长度的影响，与基本全分离系数的大小无关，无论在哪种情况下，都能稳定收敛到10-14量级以上。精度完全能满足稳定同位素分离工艺对算法精度的要求。

4 结论

本研究提出了一种新的求解多组分级联方程的数值计算方法。该方法以针对迭代序列差的迭代法求解级联各级的分离方程，以各级丰度混合条件即级间管道的连接方式作为求解各级分离方程的约束条件，以级联组分守恒方程为收敛判据进行了级联数值计算，通过与其他计算方法得到的结果进比较，论证了本计算方法的准确性。同时，本计算方法在计算相对分离系数很大、组分很多、级联很长、级联分流比很小或接近全回流等特殊情况下的级联时，都能稳定收敛，计算能力。

本算法可以很方便地推广到带附加流级联、层架级联、非对称级联等复杂级联的计算。

参考文献：

[1] Xie Quanxin, Sulaberidze GA, Borisevich VD. Optimization of Model cascades for Multicomponent Isotope Mixtures [C]//Physical and Chemical Processes on Selection of Atoms and Molecules :Proceedings of XI All-Russia (International) Scientific Conference. December 11-15, 2006: 15-20.

[2] 谢全新，李大勇，李文泊，等. 多组份同位素分离级联的优化[J]. 核科学与工程，2008， 28 (1)：86-91.

Xie Quanxin, Li Dayong, Li Wenbo, et al. Cascade optimization for multicomponent isotope separation [J]. Chinese Journal of Nuclear Science and Engineering, 2008,28(1): 86-91(in Chinese).

[3] 谢全新，李大勇，吴建军. 回收铀分离级联计算[J]. 核技术，2009,32 (1): 61-65.

Xie Quanxin, Li Dayong, Wu Jianjun. Cascade calculations for separation of recycled uranium [J]. Nuclear Techniques, 2009,32 (1): 61-65(in Chinese).

[4] 周明胜，钟松，程维娜，等. 高丰度硅-28同位素分离技术 [J]. 清华大学学报:自然科学版, 2003, 43 (6): 729-731.

Zhou Mingsheng, Zhong Song, Cheng Weina, et al. Enrichment of 28Si to high concentrations by gas centrifuge [J]. J Tshinghua Univ: Sci & Tech, 2003, 43 (6): 729-731(in Chinese).

[5] 周明胜，梁雄文，张永刚，等. 离心法生产氙同位素 [J]. 同位素，2006,19 (1): 1-3.

Zhou Mingsheng, Liang Xiongwen, Zhang Yonggang, et al. Experimental study of Xenon isotopes production by gas centrifuge [J]. Journal of Isotopes, 2006,19 (1): 1-3(in Chinese).

[6] 李大勇,牟宏, 李文泊, 等.74Se 同位素分离研究 [J]. 同位素, 2006,19 (1): 4-6.

Li Dayong, Mou Hong, Li Wenbo, et al. The study of74Se isotope separation [J]. Journal of Isotopes, 2006,19 (1): 4-6(in Chinese).

[7] 周明胜，杨光伟，聂玉光. 离心法分离饿同位素的试验研究 [J]. 同位素，2004,17(1): 5-7.

Zhou Mengsheng, Yang Guangwei, Nie Yuguang. Experimental study on Osmium isotopes separation by gas centrifuge [J]. Journal of Isotopes, 2004,17 (1): 5-7(in Chinese).

[8] Xie Quanxin, Borisevich V D, Potapov D V. et.al. Multicomponent isotope mixture separations in square cascade with losses of working substances [J]. Engineering Physics, 2006, 2: 30-34 (in Russian).

[9] Xie Quanxin. Stationary molecular selective transfer in ordinary and multiflow cascades with large enrichment factors and losses at stages for the separation of multicomponent isotopic mixture [D]. Moscow: Moscow Engineering Physics Institute, 2007.

[10] Zeng Shi, Ying Chuntong. A robust and efficient calculation procedure for determining concentration distribution of multicomponent mixtures [J]. Separation Science and Technology, 2000, 35 (4): 613-622.

[11] Zeng Shi, Ying Chuntong. A method of separating a middle component in multicomponent isotope mixtures by gas centrifuge cascades [J]. Separation Science and Technology, 2000, 35 (14): 2 173-2 186.

[12] Wu Hongjiang, Ying Chuntong, Liu Guanjun. Calculation methods for determining the distribution of components in a separation cascade for multicomponent mixture [J]. Separation Science and Technology, 1998, 33 (6): 887-898.

[13] Zeng Shi, Ying Chuntong. A second-order time-accurate method for determination of concentration distribution of multicomponent mixtures in separation cascades[J]. Separation Science and Technology, 2000, 35 (5): 729-741.