浅谈直观教学在小学数学教学中的作用
2014-06-11黄凤梅徐红梅
黄凤梅 徐红梅
摘 要:直观教学在小学数学教学中是非常重要的。直观教学不仅能把抽象的数学知识具体化、形象化,使学生易于理解和掌握;直观教学还能使学生对所学知识有充足的感性体验,使其对知识的记忆更加深刻;直观教学让学生在研究解决问题的过程中获得更多的发展。
关键词:直观教学 优越性 获得更多发展 理解复杂数量关系
中图分类号:G623.5 文献标识码:A 文章编号:1673-9795(2014)02(c)-0019-01
1 同课异构,凸显直观教学的优越性
在看了吴正宪老师对课例“用连乘的方法解决问题”的分析后,感觉直观教学能让学生体验解决问题策略的多样性。
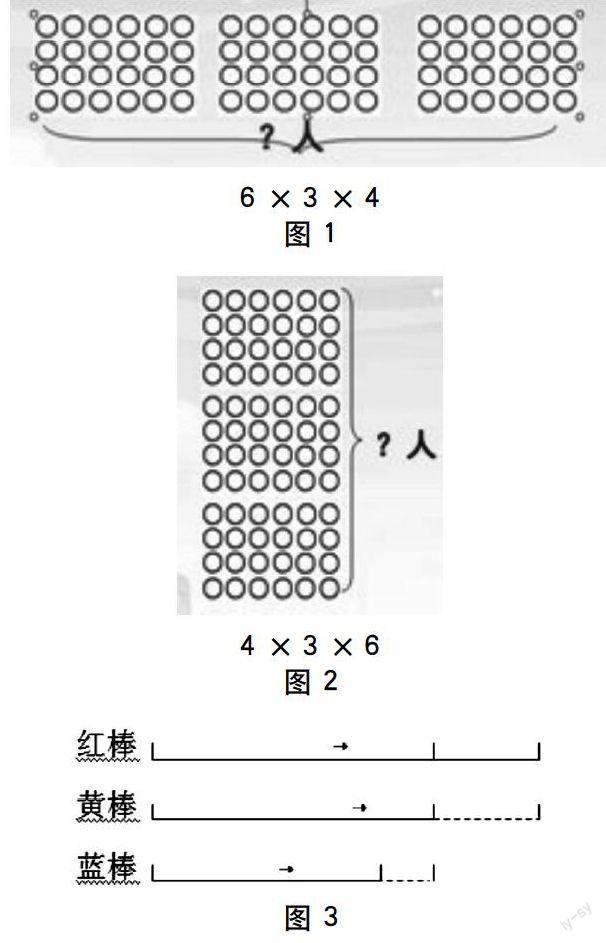
案例:用连乘的方法解决问题。课例一:出示问题:小明在像册里放照片。每页放2行,每行放4张,3页一共放多少张?(没有图示)学生经过小组讨论研究学生得出两种解法。第一种解法:从条件分析,知道每页放2行,每行放4张,可以求出每页放多少张。知道每页放多少张,就可以求出3页一共放多少张2×4×3。第二种解法:求3页一共放多少行?再求3页一共放多少张?2×3×4。课例二:每个方阵有4行,每行有6人,一共有3个方阵。一共有多少人?(并附有图示)经过小组学习,得出了3种方法。方法1:知道每个方阵有4行,每行有6人,可以求出一个方阵有多少人,再求3个方阵有多少人6×4×3。方法2:横着观察把3个方阵看成一个方阵,先求一行有多少人,再求4行一共有多少人。(见图1)方法3:竖着观察把3个方阵摞起来看成一个方阵,先求共有多少行,再求共多少人。(见图2)
通过两个课例的比较,可以看出直观教学的优越性。同时,我们也深刻的体验到,问题解决活动的价值不只是获得具体问题的解,更多的是学生在问题解决过程中获得的发展。其中重要的一点在于使学生学习一些问题解决的基本策略,体验问题解决策略的多样性,并在此基础上形成自己解决问题的某些策略。
2 直观教学让学生在数学学习中获得更多的发展
案例:我在和学生一起学习体积单位间的进率时是这样组织课堂教学的。准备一个粉笔盒(体积大约1立方分米)和一些玩具骰子(体积大约1立方厘米)。首先让学生估计粉笔盒和一个玩具骰子的体积大约是多少,学生很快说出粉笔盒体积大约1立方分米,一个玩具骰子的体积大约是1立方厘米。然后我又问,这个粉笔盒大约能盛下多少个骰子。学生纷纷猜起来,100、500、300……答案不一。在猜的氛围中我提出了用事物来摆一摆验证一下,看看谁猜的更接近一些。学生纷纷动手摆起来。不一会就有学生发言了:老师,这样摆太麻烦了,还不如在摆的基础上算一算,这样快。我便趁此机会让学生推算能盛下多少个。学生:先摆上一行,这一行能摆10个,再往后排,能排10行,这一层一共是10×10=100(个)上面还能摆10层,所以一共能摆100×10=1000个,这个粉笔盒大约能盛1000个玩具骰子。有的学生顿时惊讶起来:能盛下1000个,这么多呀。在此基础上,我便提出了1立方分米=( )立方厘米的问题。学生通过自己的思考很快就得出了答案1立方分米=1000立方厘米。
反思这节课的教学,学生在这一节课的收获太多了。首先,估算能力得到了进一步的提高和发展。从刚开始猜的100到最后得出的1000可以体验到。其次,对知识的记忆更加深刻。从“猜”到“摆”再到“体验麻烦”再到“算”学生经历了一系列的思考,对1立方分米=1000立方厘米记得就深刻扎实。再次,发展了学生的空间观念。在“猜、摆、算”的过程中,让学生进一步体验了1立方分米、1立方厘米的大小以及他们之间的关系,发展了学生的空间观念。直观教学不仅能把抽象的数学知识具体化、形象化,使学生易于理解和掌握;直观教学还能使学生对所学知识有充足的感性体验,使其对知识的记忆更加深刻;直观教学让学生在研究解决问题的过程中获得更多的发展。
3 直观教学有利于学生理解较复杂应用题的数量关系
利用直观教学中的画线段图可以帮助学生理解较为复杂的应用题的数量关系。
3.1 画线段图可以将应用题化难为易
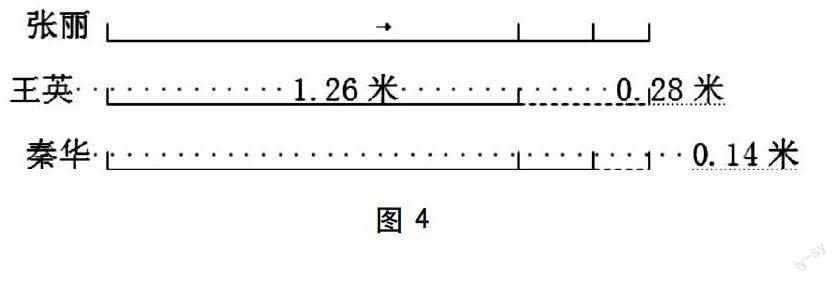
例如,解决这样一道题:有红、黄、蓝三根彩棒,红棒比黄棒长2/3米,蓝棒比黄棒短1/6米。红棒与蓝棒相差多少米?如果蓝棒比黄棒长2/9米,红棒与蓝棒相差多少米?对于第一问,题中只告诉我们“红棒比黄棒长1/3米,蓝棒比黄棒短1/5米”,并没有具体告诉红棒、蓝棒、黄棒其中任何一根的长度,不知道具体数量怎么办?我们不妨通过画线段图来解答(见图3)。
通过线段图,我们可以很清楚地看到,红棒与蓝棒相差“1/3+1/5=8/15(米)”。用同样的方法,我们可以很快算出第二问的答案。
3.2 画线段图可以将应用题化繁为简
例如这样一道题:王英身高1.26米,比张丽矮0.28米,秦华的身高比张丽矮0.14米。秦華和王英比,谁高一些?高多少米?根据问题和题中的已知条件,同学们一般会这样去做:1.26+0.28=1.54(米),这是张丽的身高;1.54-0.14=1.40(米),这是秦华的身高。王英的身高1.26米与秦华的身高1.40米比较,1.26<1.40,所以秦华高,高1.40-1.26= 0.14(米)。而这道题通过画线段图去解答,就简便得多(见图4)。
从图中很容易看出秦华比王英高,高0.28-0.14=0.14(米)。
参考文献
[1] 陈鸿绪.浅谈几何直观在小学数学教学中的运用[J].小学教学参考:数学版,2013(2):56.
