非连续边界层对圆柱声学共鸣频率的影响研究

尹钊玮， 冯晓娟， 林 鸿， 张金涛

（中国计量科学研究院热工计量科学研究所，北京 100013）

非连续边界层对圆柱声学共鸣频率的影响研究

尹钊玮， 冯晓娟， 林 鸿， 张金涛

（中国计量科学研究院热工计量科学研究所，北京 100013）

基于声学一阶微扰理论，建立了低压下由于气-固界面的温度阶跃和速度滑移带来的边界层不连续性对圆柱声学共鸣频率的扰动规律，进一步发展了圆柱声学共振频率的非连续边界层修正模型，计算了非连续边界层对4种惰性气体、不同声学模式和不同压力及温度的影响。分析研究显示，气体处于低压状态时，温度阶跃和速度滑移会使声学共振频率发生偏移，不引入声能损耗。在50 kPa时，非连续边界层对声学共鸣频率的影响可达10× 10－6，表明非连续边界层修正项对于10－6不确定度水平的尖端声学共鸣测量，是一个重要的不确定性来源。

计量学；圆柱声学共鸣；边界层；温度阶跃；速度滑移

1 引 言

气相声速是目前可测量的具有最小不确定度的热物性之一，是热力学科学研究和热工技术应用的重要基础参数［1］。声学共鸣法是国际计量界重新测定Boltzmann常数，并由此重新定义热力学温度单位开尔文（K）的研究中，具有最小测量不确定度的方法［2，3］。气相声速通过准确测定共鸣腔内工质气体的理想共振频率和共鸣腔几何尺寸计算得到。然而实际的声学共鸣腔中，各种非理想因素会对共鸣腔内气体的理想共振模式带来扰动［4，5］。为了追求玻尔兹曼常数确定的相对标准不确定度达到1× 10－6水平，就必须对这些非理想因素对声学共鸣频率的扰动作用机理进行深入研究，并给予合理修正。

热边界层和粘性边界层是影响声学共鸣法测量不确定度的最主要来源。实际的工作气体是有粘性的。有声学共鸣时，气体介质在声学共鸣腔内运动，会在圆柱声学共鸣腔内壁上形成对共振频率有扰动的粘性边界层和热边界层；两个端盖与工作气体有热交换；低压条件下，实际工作气体与共鸣腔内壁存在温度和粘度不连续的滑移边界条件。这些因素共同作用，形成有能量与动量梯度的热和粘性边界层。这种热交换和粘滞性引起的声阻抗，会使测量的声学共鸣频率发生偏移，需要对系统偏差修正［6］。根据流体力学理论，可以很好地对边界层效应给于修正，但因为腔内气体与壁面之间存在温度梯度，在低压区无法给出准确的热边界层修正值。Ewing等针对圆球谐振腔的温度阶跃问题提出了理论修正［7］。

本文研究了圆柱共鸣腔中不同声学模式下非连续边界层对圆柱声学共振频率的影响，给出了扰动准确修正的分析模型，并实现了扰动修正。

2 理论基础

理想情况下声波在圆柱形共鸣腔内传播，其波动方程的本征波函数φN为：

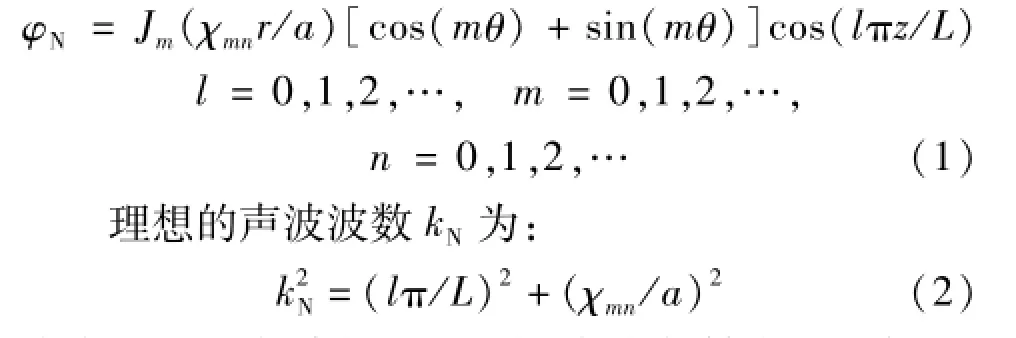
式中，r，θ，z分别为圆柱径向、角向与轴向极坐标，l、m、n分别为轴向、角向和径向共振模式的量子数，Jm为m阶柱Bessel函数，χmn为dJm（x）／d x＝0的第n个根，L和a分别为圆柱腔的腔长和半径，特征值kN为波数，且kN＝ω／c，c为声音在工质中传播的速度，ω为角频率。

根据波数与频率关系可知，理想共振频率为：

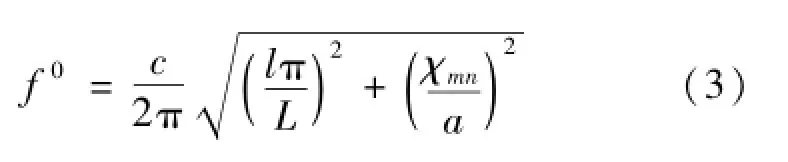
在共振频率的实际测量中，由流体的粘滞性和热传导引起的边界层效应、开孔、壳体振动以及分子弛豫等非理想因素，使得实测的共振频率fN偏离了理想共振频率f0，并且变成了有一定宽度的尖峰［8］。用复数表示实际测量的共振频率：

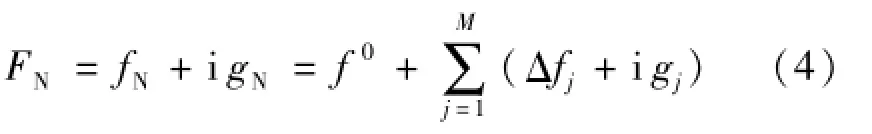
式中，fN表示实际测量的共鸣频率，gN表示实际测量的频率半宽，定义为声压衰减到振幅1时距离共振频率中心的频率偏差，Δfj和gj为第j个非理想因素对共振频率和频率半宽的影响。

根据声学一阶微扰理论，可以得到气体工质与壁面之间热边界层和粘性边界层对理想波数kN的扰动计算公式：

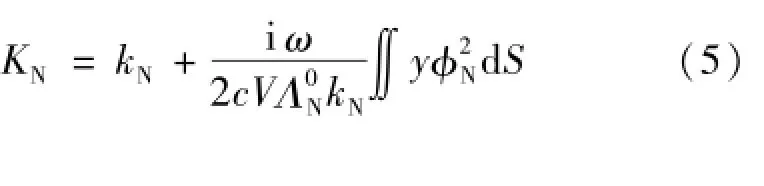
式中，V为圆柱腔体积，Λ0N为归一化常数：

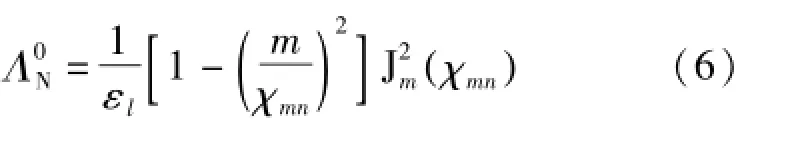
式中，ε0＝1，εl＞0＝2。

热边界层和粘性边界层非理想因素对共振频率和频率半宽的影响可表示为［9］：

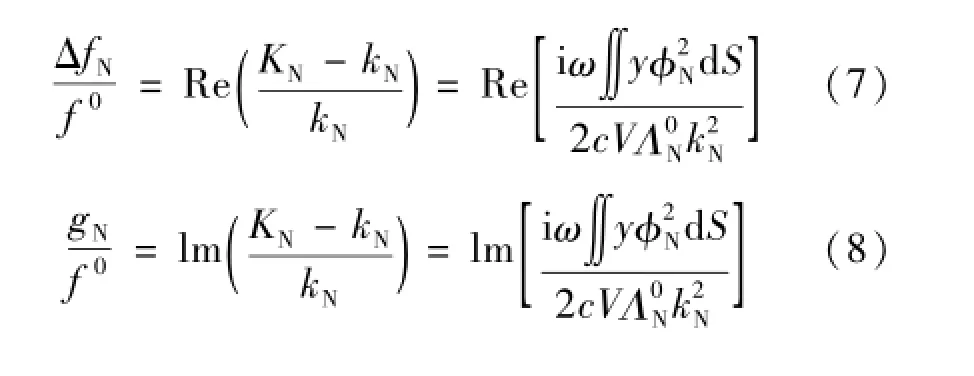
3 非连续边界层修正

在气体压力较低时，流体力学理论就无法准确描述边界层处的变化。在边界处，气体分子会表现出能量和动量的不连续性变化，这种现象被称为温度阶跃和速度滑移。纳维-斯托克斯等指出，分子平均自由程lm＝lg（lg为分子振动波长）。传统的边界层理论认为实际气体与壳体表面处气体之间导热系数相等，温度变化可以忽略，气体分子在气固表面处的切向速度为0。但气体压力较低时，需要考虑有限分子平均自由程，相同的温度梯度变化，气固表面之间的能量传递小于气气表面的传递，是因为这种情况下，分子只能单向移动，即移动到表面或离开表面。基于气固边界条件，分子的切向速度无法在边界处达到平衡，同时为了满足稳定的温度分布，即气体与壁面的热流密度相等，就要使温度梯度在该处增大。非连续性边界层的干扰如图1所示：

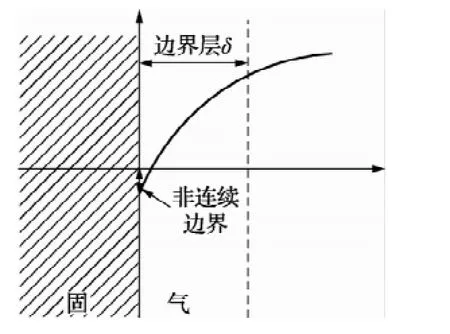
图1 圆柱共鸣腔非连续边界层示意图

根据动力学理论，能量与动量的不连续性为：

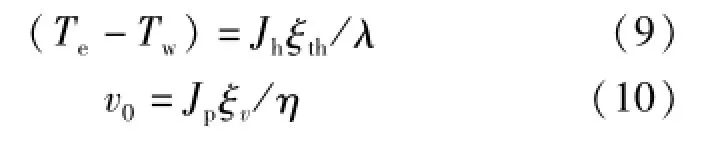
式中，Te为气体温度，Tw为壳体壁面温度，v0为滑移速度，λ为流体的导热系数，η为流体的粘度，Jh是流向壳体表面的能量流密度，Jp是流向壳体表面的动量流密度，热ξth与粘性ξv适应长度：

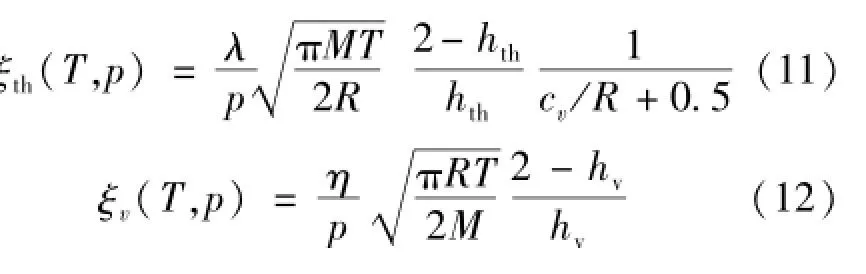
式中，M为气体的分子量，R为通用气体常数，cv为定容比热容。热适应系数hth定义为实际通过壳体表面传递的热能与气体和壳体表面达到热平衡时传递的热能之比ΔE1／ΔE2，粘性适应系数hv定义为实际通过壳体表面分子的动量与气体和壳体动量平衡时分子动量之比。hth与hv均与壳体表面材质，特别是分子吸收层有关。

考虑热边界层长度δth，粘性边界层长度δv，温度阶跃适应长度ξth和分子滑移引起的适应长度ξv，可以得到圆柱共鸣腔柱面的声导纳yside和端面的声导纳yend为：

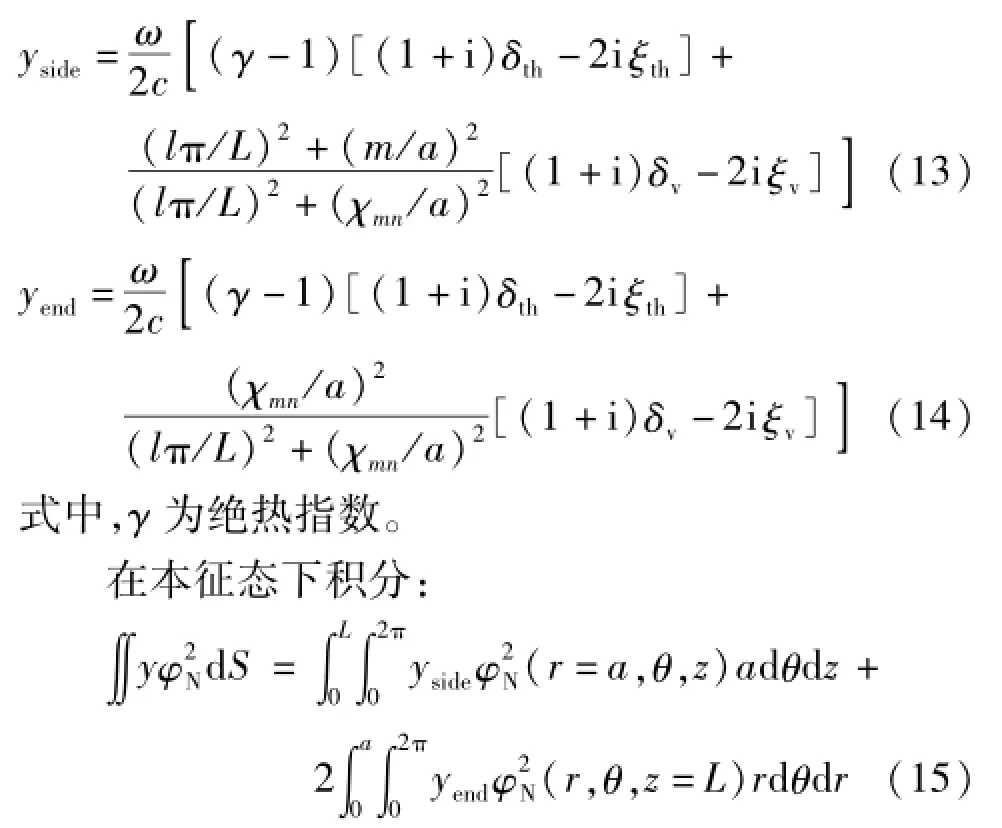
只考虑温度阶跃和速度滑移对共鸣频率的影响，可以得到非连续边界层对圆柱腔体的理想谐振频率的偏移为：

式中，Δfth和Δfv为温度阶跃和速度滑移对共鸣频率的偏移，并且非连续边界层对共振峰的半宽没有影响，即不会导致声能的耗散。从式（16）和式（17）可以看出，Δfth和Δfv对理想谐振频率的相对偏移量与谐振频率无关，只与气体物性和热力学性质，以及腔体尺寸有关。

4 讨论和分析

氦（He）、氩（Ar）、氪（Kr）和氙气（Xe）是测量Boltzmann常数的工质气体。对于这4种气体，图2和图3分别给出了非连续边界层对纯轴向和纯径向声学模式理想谐振频率的偏移与气体压力的变化关系。其中，圆柱型共鸣腔的尺寸为长度L＝80 mm，半径a＝40 mm，气体温度为T＝273.16 K。从图中可以看出，从氦气到氩气，随着原子直径增加，非连续边界层对共鸣频率的偏移量逐渐减小，并且偏移量随着压力减小而逐渐增加。粘性适应长度随分子量增大而减小，因此速度滑移对共振频率的扰动亦随分子量增大而减小，这种差异在压力较低时更为明显。对于氦气，在压力p＝20 kPa时，温度阶跃影响超过了60×10－6，这个修正量对于测量玻尔兹曼常数达到1×10－6的要求十分重要。速度滑移对频率的偏移要小于温度阶跃的影响，但对氦气的影响仍然达到了10×10－6左右。非连续边界层对纯轴向声学共鸣频率的偏移量要大于纯径向模式。图4和图5分别给出了对于这4种气体，非连续边界层对纯轴向和纯径向模式理想谐振频率的偏移与气体温度的变化关系，气体压力p＝50 kPa。从图中可以看出，非连续边界层对共鸣频率的改变随温度变化成正比关系，对氦气的影响要远大于其余3种惰性气体（氩、氪和氙气）。

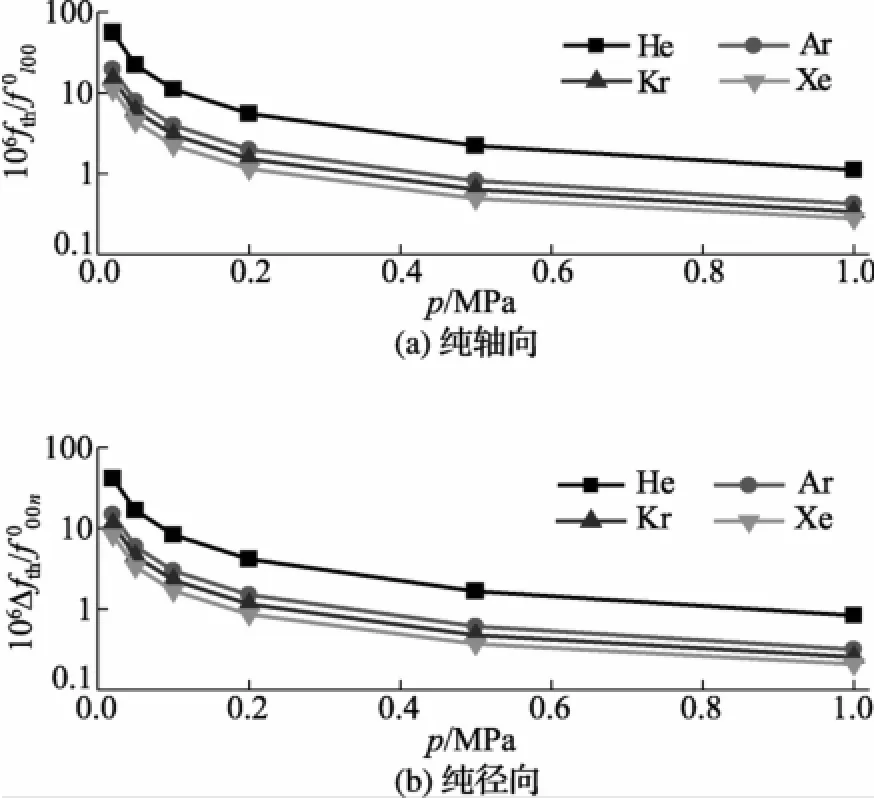
图2 温度阶跃对理想声学共鸣频率的偏移和压力关系图

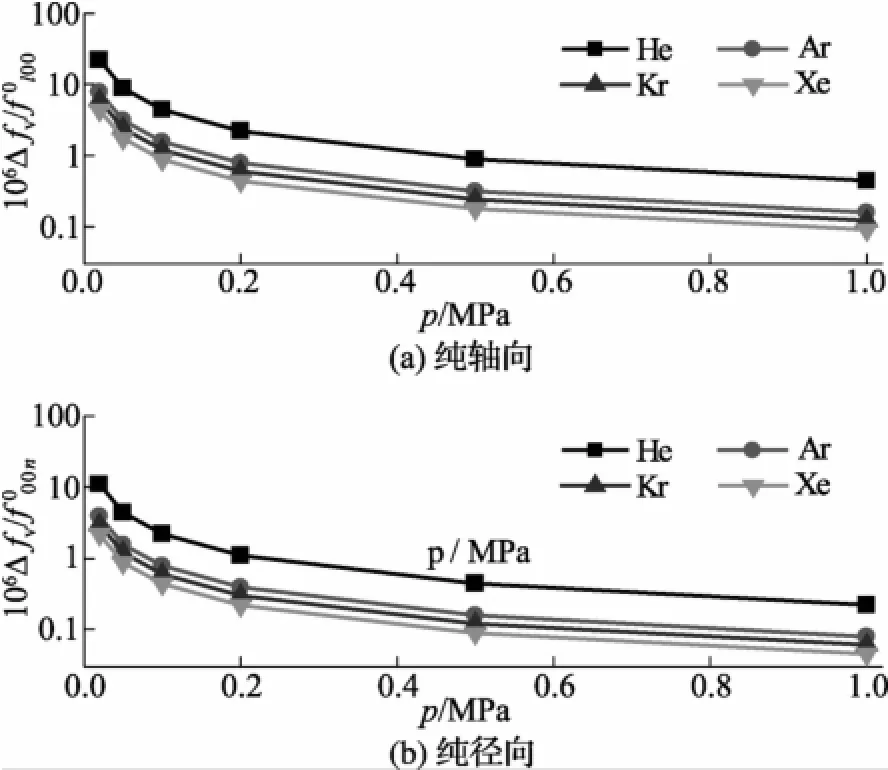
图3 速度滑移对理想声学共鸣频率的偏移和压力关系图

图4 温度阶跃对理想声学共鸣频率的偏移和温度关系图

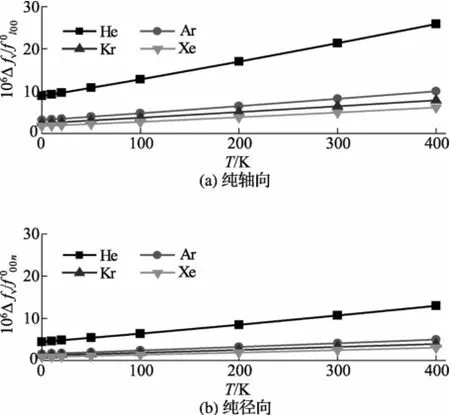
图5 速度滑移对理想声学共鸣频率的偏移和温度关系图

5 结 论

本文基于声学微扰理论，研究了非连续边界层（温度阶跃和速度滑移）对圆柱声学共鸣频率扰动机理，并建立了修正模型。分析结果表明，非连续边界层对圆柱声学共鸣频率的偏移量在低压下远大于1×10－6，并且与气体分子（原子）直径和压力成反比，与温度成正比。温度阶跃和速度滑移不会使声波能量损失，对频率半宽没有影响。对于追求不确定度达到1×10－6水平的尖端声学共鸣法测量，如测定玻尔兹曼常数，必须进行非连续边界层的扰动效应修正，才可获得更接近物理真实结果。

［1］ Moldover M R.Optimizing acoustic measurements of the Boltzmann constant［J］.CRPhys，2009，10（9）：815－827.

［2］ Moldover M R，Trusler J P M，Edwards T J，etal. Measurement of the universal gas constant R using a spherical acoustic resonator［J］.JResNatlBurStand，1988，60（4）：249－252.

［3］ Gavioso R M，Benedetto G，Merlone A，etal.Progress Towards an Acoustic Measurement of the Molar Gas Constant at INRIM［J］.IntJThermophys，2007，28（6）：1775－1788.

［4］ Zhang JT，Lin H，Sun JP，etal.Cylindrical Acoustic Resonator for the Re-determination of the Boltzmann Constant［J］.IntJThermophys，2010，31（7）：1273－1293.

［5］ 冯晓娟.高精度热物性实验系统研制与CO2／丙烷热力学性质研究［D］.北京：清华大学热能工程系，2010.

［6］ Trusler JPM.Physical acoustics and metrology of fluids［M］.New York：Adam Hilger，1991.

［7］ Ewing M B，McGlashan M L，Trusler J P M.The temperature-jump effect and the theory of the thermal boundary layer for a spherical resonator.Speeds of sound in argon at 273.16 K［J］.Metrologia，1986，22（2）：93－102.

［8］ Estrada-Alexanders A F，Trusler JPM.Speed of sound in carbon dioxide at temperatures between（220 and 450）K and pressures up to 14 MPa［J］.JChemThermodyn，1998，30（12）：1589－1601.

［9］ Morse P M C，Ingard K U.Theoretical acoustics［M］. New Jersey：McGraw-Hill，1986.

The Discontinuous Boundary Layer Effects on Acoustic Resonance Frequency in Cylindrical Cavity

YIN Zhao-wei， FENG Xiao-juan， LIN Hong， ZHANG Jin-tao
（National Institute of Metrology，Division of Thermophysics and Process Measurements，Beijing 100013，China）

Based on the first order acoustic perturbation theory，the discontinuous boundary layer effects from the temperature-jump and slip-velocity between the gas and the solid wall are investigated.At low pressures，temperature-jump and slip-velocity make a significant contribution to the resonance frequencies but not to energy losses.The corrections to the resonance frequencies are presented.The corrections for different gases，different acousticmodes at different pressures and temperatures are also compared.This correction is very necessary for the re-determination of the Boltzmann constant.

Metrology；Cylindrical resonator；Boundary layer；Temperature-jump；Slip-velocity

TB94

A

1000-1158（2014）01-0001-04

10．3969／j．issn．1000-1158．2014．01．01

2012-10-11；

2012-12-29

国家自然科学基金（51106143，50906076）

尹钊玮（1987－），女，中国计量科学研究院硕士研究生，主要从事温度计量与流体热物性的研究。yinzw＠nim.ac.cn