逆向哈特曼面形测量法中最佳针孔直径确定

马建荣， 郝 群， 朱秋东， 胡 摇

（北京理工大学光电学院，北京 100081）

逆向哈特曼面形测量法中最佳针孔直径确定

马建荣， 郝 群， 朱秋东， 胡 摇

（北京理工大学光电学院，北京 100081）

在逆向哈特曼法中，针孔光阑具有选择光线和决定测量分辨率的作用，其直径大小直接影响CCD接收器上光斑的大小以及光线在瞳面上精确位置的确定。用衍射光学理论，推导出了精确计算针孔直径的傅里叶变换表达式，并进一步给出了针孔直径的快速解析计算式。实验证明，在实际非球面面形测量中，快速估算式能够满足计算最佳针孔直径的精度要求并提高计算效率。

计量学；逆向哈特曼；面形测量；非球面；最佳针孔

1 引 言

将非球面、自由曲面等复杂曲面取代球面用于成像系统，能有效改善像质、减小系统体积和重量［1］。这类复杂光学曲面面形的高精度检测是其加工和光学系统装调的基础和前提。哈特曼测量法由哈特曼提出［2］，随后在光学检测中许多研究者采用了与其类似的原理和方法［3～6］。逆向哈特曼面形测量法［7］克服了传统哈特曼法（THT）中动态范围和分辨率难以同时提高的缺点，有效地降低了非球面测量时的光线斜率，增大了测量范围，与干涉法［8］相比，其结构相对简单，通用性好，抗干扰能力强，成本低。在逆向哈特曼法中，针孔选择光线并决定测量分辨率，本文给出了该方法中确定最佳针孔直径的傅里叶变换式，并进一步给出快速确定最佳针孔尺寸的解析式。

2 逆向哈特曼法面形测量原理及针孔的作用

逆向哈特曼面形测量法（IHSFM）的原理图如图1所示，整个系统由图像发生器、分束镜、针孔、CCD摄像机及计算机组成，其面形测量原理与THT相似，系统中的图像发生器相当于哈特曼光阑，针孔选择细光束。由于本方法中图像发生器和探测面在光路中的位置与THT中的位置相反，因此称为逆向哈特曼法。采用逆向法以后，避免了THT法中测量光线的遮挡切割问题，可测量较大非球面度的零件，而且可以使图像发生器的尺寸比传统哈特曼光阑大大减小，使整个装置小型化。

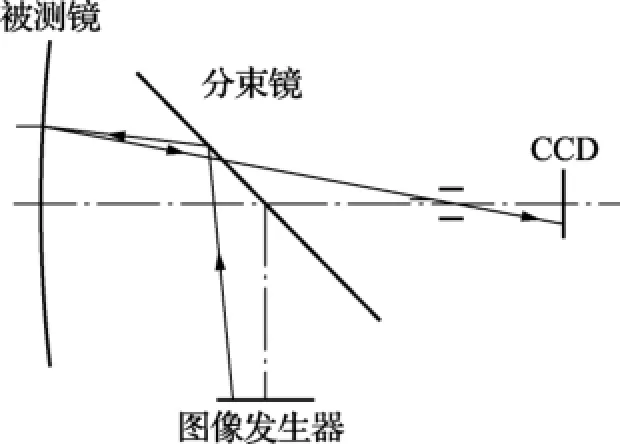
图1 逆向哈特曼测量法原理图

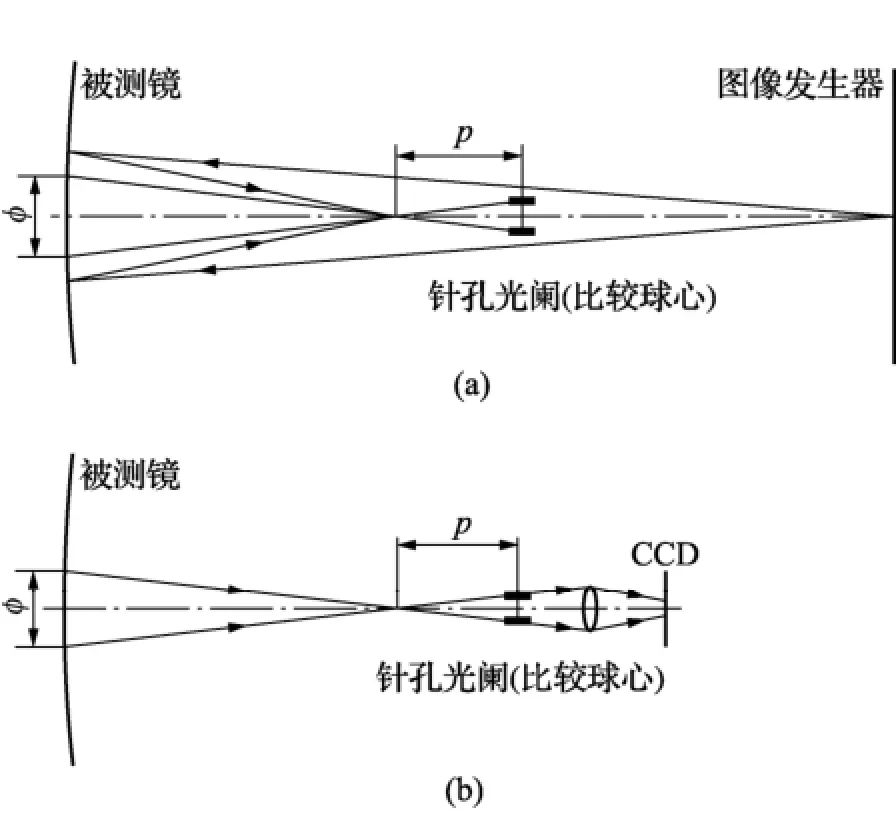
图2 被测镜上采样区域及CCD上弥散圆

在逆向哈特曼测量法中，针孔具有选择光线和决定测量分辨率的作用。由图2（a）可知，图像发生器上的点光源经被测镜后，在距针孔p处成像，像点过针孔边缘的光线反向延长后，在被测镜上的对应区域就是被测镜上的采样区域，采样区的直径大小φ决定了采样分辨率。由于CCD对被测面成像，图像发生器的像在CCD上有离焦，如图2（b）。因此，随针孔直径减小，衍射效应变大，CCD上的光斑尺寸增大；而针孔尺寸增大则弥散圆增大，光斑尺寸也增大。只有在二者之间找到一个最佳针孔值，才能使CCD上的光斑直径最小。这样既在被测面上得到合理的分辨率，又使测量效率较高，因此，优化针孔直径是实现该方法的关键因素之一。

3 基于衍射理论的复振幅计算及光斑直径仿真

由于衍射计算的复杂性，目前没有点光源经针孔和透镜之后在任意探测位置的复振幅分布解析表达式，来计算针孔直径与复振幅分布的关系，因此需要通过两次菲涅尔衍射近似，得到探测面上的复振幅表达式，然后用离散傅里叶变换的方法得到针孔直径与复振幅分布的关系。所采用的衍射光路如图3所示。

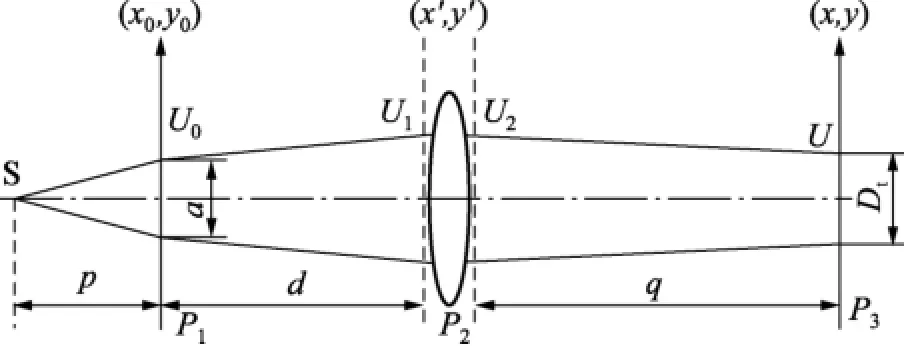
图3 球面波照明针孔的衍射光路

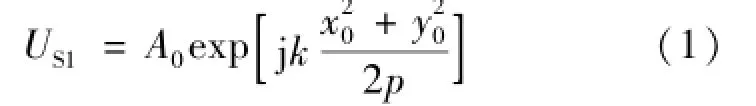
式中：A0为复常数，p为点光源S（即像点）到针孔平面的距离，k为波数。

透过物体的光波复振幅分布为

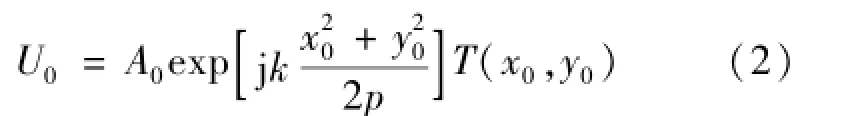
从点光源S发出的单色球面波，在物平面（针孔平面）P1上的振幅分布为

式中：T（x0，y0）为衍射针孔的复振幅透射系数。

从针孔平面P1到透镜孔径平面P2，光波的传播符合菲涅尔衍射，到达透镜孔径平面的光波复振幅U1（x′，y′）可表示为

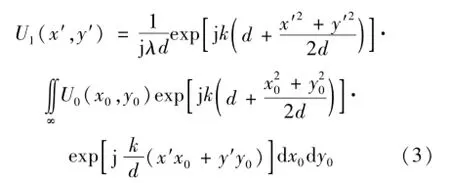
式中：λ为波长，d为物平面（针孔平面）到透镜孔径平面的距离。

考虑到透镜的位相变换因子，并假设透镜的孔径不受限制，于是由透镜出射的光波复振幅分布为

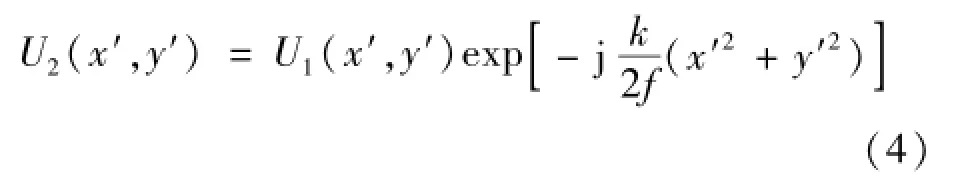
式中f为成像透镜焦距。

光波由透镜的出瞳面到探测平面P3的传播仍然符合菲涅尔衍射，传播距离为q，再次应用菲涅尔公式，可得到（x，y）平面上光波的复振幅分布U（x，y），表示为

将式（3）（4）代入式（5），经过化简，可以得到

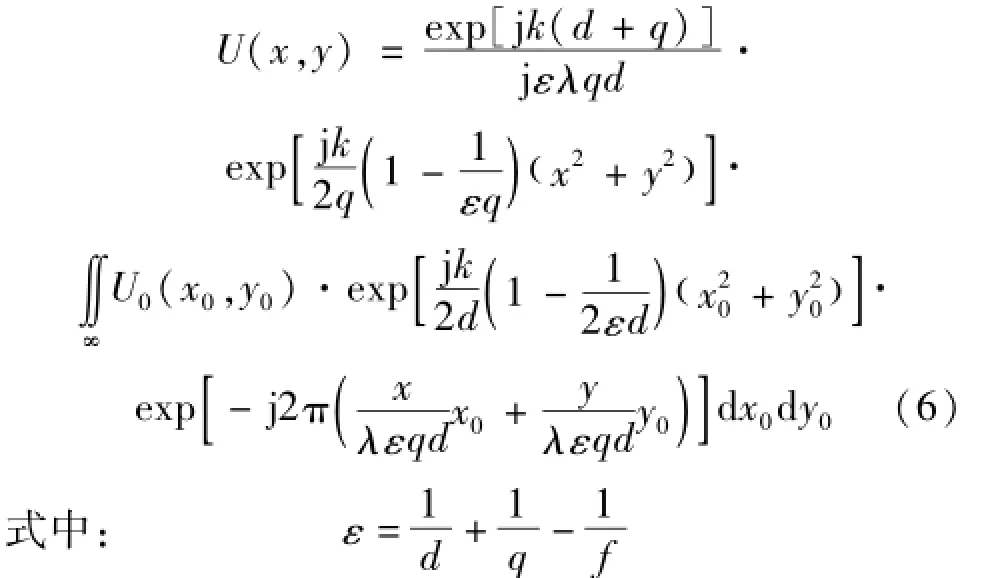
由式（6）可以看出，点光源S在P3面上的光场分布U（x，y）等于透过针孔的光波复振幅U0与一个二次位相因子的乘积经傅里叶变换后，再与另一个位相因子的乘积。式（6）包括了衍射和弥散，因此由式（6）可得到任意p、d、q情况下对应针孔的光斑直径D。由式（6）数值仿真得到的光斑辐照度分布图如图4所示，图4中横坐标r是与复振幅对应的光斑半径，纵坐标为观察面上各处辐照度与中心辐照度之比L（φ）／L（o），辐照度L＝U·U*。假设p＝7.505mm，d＝17.640mm，q＝20.233mm，f＝17.640mm，可以仿真计算出不同针孔直径a时探测器上的光斑直径Dt，计算结果如表1所示。

表1 数值仿真计算的光斑直径mm

由表1可知，为得到光斑直径Dt最小时的针孔直径a，可用式（6）迭代计算，得到最佳针孔的精确值，但是计算复杂、效率低，可以此作为参考值，用于评估快速简易算法的可靠性。

图4 衍射光斑辐照度分布图

4 最佳针孔直径的快速确定

在实际应用中，针孔直径需要根据被测镜参数和测量分辨率要求进行变化，因此有必要研究快速确定最佳针孔直径的方法。由于探测面上所得到的光斑，是针孔的衍射效应和CCD离焦造成的弥散二者共同作用的结果，爱里斑和弥散圆都可以简单快速计算得到，研究爱里斑和弥散圆的关系，可探索一种快速估算最佳针孔直径的方法。

爱里斑直径的计算表达式为

由图5所示光路，用几何光学方法可推导出探测面上的弥散圆直径表达式爱里斑半高宽的计算公式为

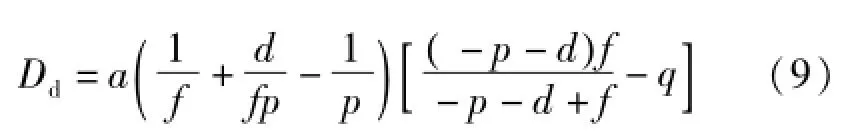
式（9）中所有变量均取绝对值。

图5 弥散圆形成光路图

在本方法中，针孔位于成像透镜的前焦面上，即d＝f，因此式（9）可以化简为

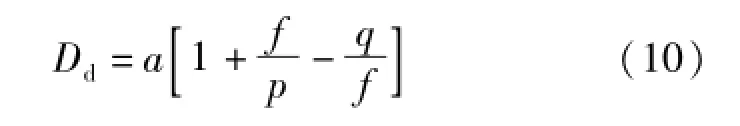
被测镜与CCD探测器是物像共轭关系，可以得到探测器与透镜的距离式中：d0为针孔到被测镜顶点的距离，取绝对值。

用数值计算可以得到p、d、f、q确定时，不同针孔直径a下的爱里斑直径DA、半高宽DA，0.5L（o）、弥散圆直径Dd，以及光斑直径Dt，如表2所示。

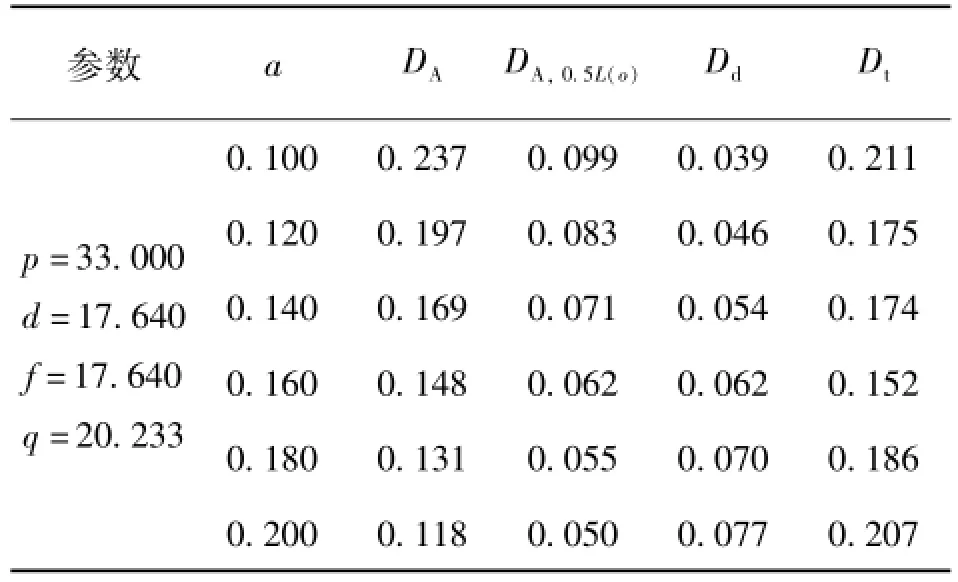
表2 不同针孔对应的计算值mm

由表2可知，当弥散圆直径等于爱里斑半高宽时，光斑直径有达到最小的趋势，因此取弥散圆直径等于半高宽，作为快速确定最佳针孔直径的条件，即

由式（8）、式（12）可以得到最佳针孔直径a与λ、p、d0的关系，即

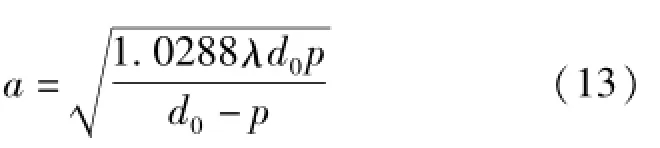
用式（13）即可计算出表2所给参数条件下的最佳针孔直径a＝0.1605mm，而由式（6）迭代计算得到的针孔直径为a＝0.1601mm。

5 实验验证

为了验证以上所提出的快速确定最佳针孔直径的条件，对表2所示的仿真结果，用曲率半径R＝120mm的凹球面镜，进行了实际光斑直径测量。探测器采用1／2 in（12.7mm）、分辨率1280×1024像素的CCD。调整点光源S到针孔的距离p，分别进行了2组实验。实验所用的装置和实验图象如图6所示，2组实验的结果如表3所示。其中D′t为探测到的光斑直径。

图6 实验装置及采集图像

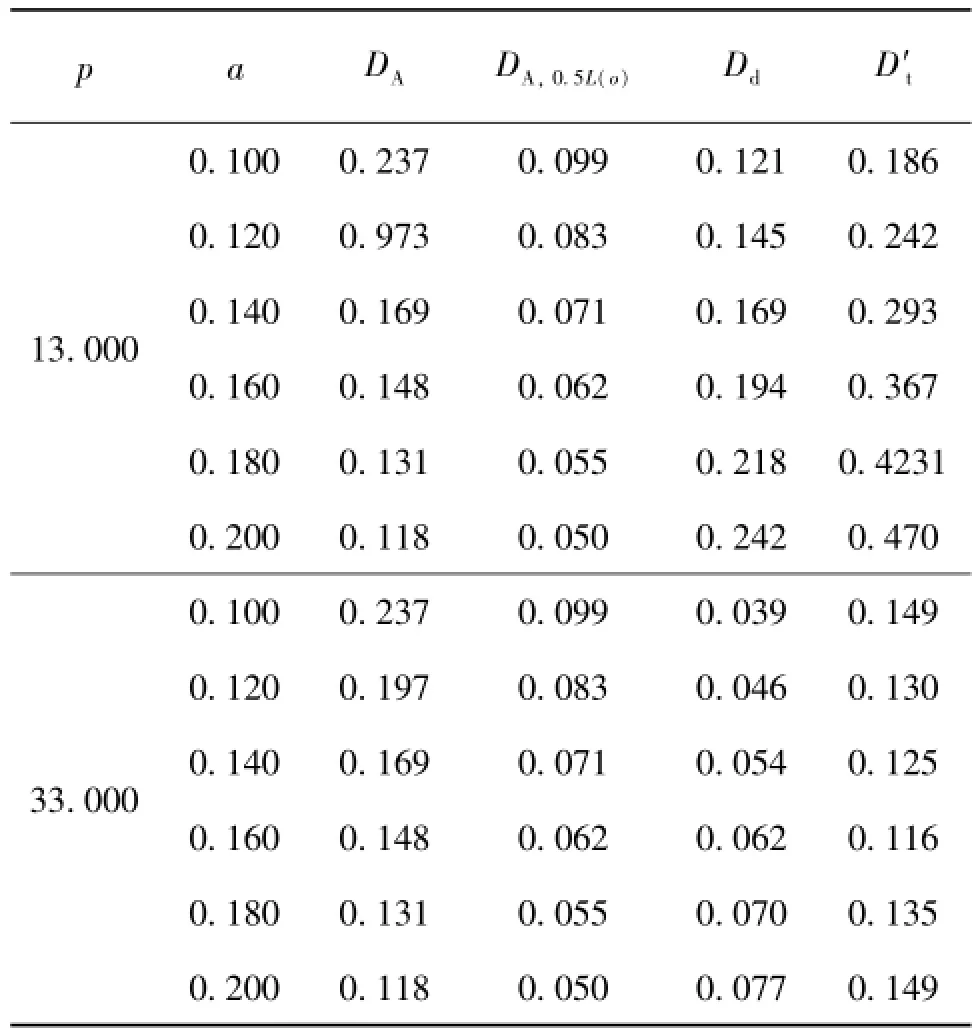
表3 确定最佳针孔直径的实验数据mm

由表3可以看出，当p＝13mm、针孔直径a＝0.140mm时，爱里斑直径等于弥散圆直径，此时CCD上的光斑直径D′t并不是最小值；而当p＝33 mm，针孔直径a＝0.160mm时，弥散圆直径等于半高宽，此时测得的光斑直径最小。因此，利用式（13）计算最佳针孔直径，是逆向哈特曼面形测量法中快速确定最佳针孔直径的便捷计算法。

6 结 论

在逆向哈特曼面形测量法中，针孔具有选择光线和决定测量分辨率的作用，并影响检测效率。本文通过理论分析，给出了用衍射光学方法计算最小光斑时针孔直径的傅里叶变换公式，但计算复杂，在此基础上提出了快速确定最佳针孔直径的方法。通过理论仿真和实验验证证明，当弥散圆直径等于半高宽时，在CCD上所得光斑尺寸最小，从而给出了最佳针孔直径估算的解析表达式，可以方便快速得到最佳针孔的尺寸。

［1］ Seiferta L，Prussb C，Dörbandc B，etal．Measuring Aspheres with a chromatic Fizeau Interferometer［C］／／Proc SPIE，Munich，Germany，Optical Measurement Systems for Industrial Inspection VI，2009，7389：1－9.

［2］ Hartmann J.Objektivuntersuchungen［J］.Zt．Instrumentenkd，1904，24：1.

［3］ Korovyakovskii Yu P.Use of the Hartmann method for testing the surface of the 6-meter LATmirror under shop conditions［J］.SovietJournalofOpticalTechnology，1977，44（11）：649－651.

［4］ Snezhko L I.On theaccuracy of the Hartmannmethod for testing aspherical wavefronts［J］.SovietJournalofOptical Technology，1980，47（9）：505－508.

［5］ Lane R G，Tallon M.Wave-front reconstruction using a Shack-Hartmann sensor［J］.AppliedOptics，1992，31（32）：6902－6907.

［6］ 刘丹，闫岩，任冰强，赵永凯，等.扫描型哈特曼检测装置研究［J］.强激光与粒子束，2005，17（9）：1377－1381.

［7］ 马建荣，郝群，朱秋东，等.基于球坐标的逆向哈特曼面形测量法［J］.计量学报，2013，34（1）：11－15.

［8］ 吴继宗，戴晓芳，采振祥.应用干涉型计算机全息图检测非球面［J］.计量学报，1987，8（4）：271－277.

中国计量测试学会科学技术进步奖简介

为调动广大计量测试科技工作者的积极性和创造性，促进计量测试领域科技人才的成长，全面推动计量测试科技创新和进步，经国家质量监督检验检疫总局同意并报国家科学技术部、国家科学技术奖励工作办公室核准，中国计量测试学会特设“中国计量测试学会科学技术进步奖”（登记证书编号：国科奖社证字第0234号），以奖励在计量测试领域科学研究、技术创新与开发、科技成果推广与应用以及实现产业化方面取得卓著成绩或者做出突出贡献的个人和集体。

中国计量测试学会科学技术进步奖每年评奖一次，分基础科研类和应用技术类。

参与评奖单位的范围为：中国计量测试学会会员单位及个人。

具体管理办法、申报程序、申报要求等详见中国计量测试学会网站： http：／／www.china－csm.org

联系方式：中国计量测试学会科学技术进步奖奖励办公室

联系人：刘健； 电话：010－84639756； 手机：13683304590

通讯地址：北京市朝阳区育慧南路3号西单元五层506室

E-mail：csm_jiang＠126.com

The Best Diameter Determ ination of the Pin Aperture in Inverse Hartm ann Surface Form Measurem ent System

MA Jian-rong， HAO Qun， ZHU Qiu-dong， HU Yao
（School of Optoelectronics，Beijing Institute of Technology，Beijing100081，China）

In the inverse Hartmann surface form measurement，the pin aperture selects light reflected from the test surface and determines themeasurement resolution.The diameter of the pin aperture has influence on the size of light spots on CCD and the accuracy of determining the ray location on the pupil.The Fourier transform expression for precisely calculating the pin aperture diameter is derived from diffraction optics theory.Moreover，an estimation formula which directly calculates the diameter of the pin aperture is also derived.Simulation and experiment show that the fast estimation formula canmeet the accuracy and effectively save time when calculate the best diameter of the pin aperture in realmeasurement.

Metrology；Inverse Hartmann system；Surface form measurement；Aspheric surface；Best pin aperture

TB96

A

1000-1158（2014）01-0039-05

10．3969／j．issn．1000-1158．2014．01．09

2012-03-26；

2012-07-31

国家自然科学基金（61078044）

马建荣（1972－），男，甘肃平凉人，北京理工大学高级工程师，在读博士研究生，主要从事光学精密测量及仪器研究。mjr8868＠163.com