红外辐射温度计的辐射源尺寸效应修正

原遵东

（中国计量科学研究院，北京 100013）

红外辐射温度计的辐射源尺寸效应修正

原遵东

（中国计量科学研究院，北京 100013）

红外辐射温度计在低温测量的辐射源尺寸效应（SSE）的规律不同于高温测量。基于以虚拟探测器温度消除背景辐射影响的SSE计算模型，推导了在不同源尺寸和不同背景条件下辐射温度计输出的SSE影响修正公式；得出不同源尺寸条件下辐射温度计温度示值的SSE影响修正的理论解析表达式。在源温度低于或接近背景温度时修正模型与高温测量SSE修正模型有显著差异。所得结果适用于任意温度下对单波段辐射温度计的SSE影响修正。

计量学；辐射源尺寸效应；虚拟探测器温度；背景辐射；辐射温度计；温度修正

1 引 言

理想辐射温度计的测量结果只与其瞄准的目标的辐射亮度有关，而实际辐射温度计的输出还与目标以外的背景辐射的强弱有关，表现为输出信号与被测辐射源的大小及亮度有关，被称为辐射温度计的辐射源尺寸效应（size-of-source effect，SSE）。SSE是辐射温度计光学元件和光学系统中灰尘引起的散射、透镜表面间的相互反射、光学系统的像差及衍射等效应的综合结果［1，2］。SSE是影响辐射测温法温标复现、传递、比对和测温的主要不确定度因素之一［3，4］。国际电工委员会IEC制定的辐射温度计标准将SSE列为温度计的重要性能参数，规定温度计的不确定度指标应说明与之相应的测量距离和源直径［5］，并将在后续标准中提供对SSE的测量方法。

SSE测量［1，6～8］可采用直接法、间接法和扫描法；低温测量中的SSE测量，应修正辐射源以外的背景辐射对测量的影响［6，9］。合理的设计可减小辐射温度计的SSE［10］。Bloembergen P根据实际辐射温度计特性总结了SSE函数的经验解析表达特性［11］，Saunders P分析了直接法、间接法测量SSE的定义的差异和测温中的修正方法［12］。SSE对温度基准、标准和工业测温的影响是各国计量院的研究热点。

中国计量科学研究院研究了高温测量中SSE影响的一般性修正公式，适用于温度计输出信号与被测亮度成正比的情形［1，2］；实验研究了标准辐射温度计的不同设计对SSE的影响［13－15］，将可调焦基准高温计的SSE减小到1×10－4；分析了间接法SSE测量装置的3种不理想因素的影响［16］。为了适用于低温测量，提出消除背景辐射影响的SSE计算模型［17］。

然而，对于大多数工业辐射温度计和标准辐射温度计，SSE对测温的影响与其声称的测温不确定度水平相比不能忽略，甚至可能超过声称的不确定度水平数倍。SSE对测温的影响修正成为减小测温误差和不同测量结果之间比较的重要环节。

本文针对应用中占绝大多数的单一波段的辐射温度计，阐述了能消除背景辐射影响的SSE计算模型方法，以及在此基础上的对测温结果的SSE影响修正公式，分析了本文修正模型与高温测量SSE修正模型的规律和差异，给出了典型的SSE测量结果和对测温结果的SSE修正实例。

2 SSE测量理论

2.1 SSE函数

较早研究SSE的文献是针对高温测量的。Bloembergen P等人系统地提出SSE理论［1，2，6－8］。Bloembergen P、Machin G等人在高温测量的SSE测量模型的基础上引入了辐射源之外的背景辐射修正项［6，8］。原遵东考虑了探测器温度对测温模型的影响，提出不依赖无限大辐射源的消除背景辐射影响的SSE计算模型［17］。

为了适用于对较低温度的测量，必须考虑探测器温度对辐射温度计测温模型的影响。理想辐射温度计输出函数的自变量在被测黑体辐射源温度T之外，需增加探测器温度Td，即S（T，Td）。实际辐射温度计的输出信号是处于温度Td的探测器对温度为T、半径为r的等温圆形黑体辐射源及辐射源之外的温度为Tb的等温黑体背景辐射的响应，表示为S（r，T，Td，Tb）。

测量r＝∞的辐射源时，没有源外背景，输出信号

式中，Lb为黑体的光谱辐射亮度；λ为波长；T、Td分别为被测黑体温度和辐射温度计探测器温度；S（r，T，Td，）为无背景辐射（Tb＝0 K）时的输出信号。Lb由普朗克黑体辐射定律给出

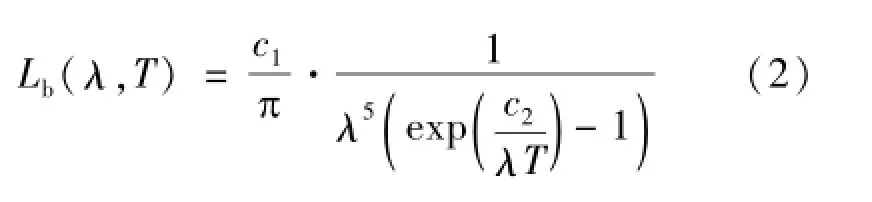
式中，c2＝0.014388 mK。

用SSE函数σ（r）表示辐射温度计对半径为r的辐射源的响应与对无限大辐射源的响应之比。设背景辐射的亮度温度（简称背景温度）为Tb。测量半径为r的辐射源时，辐射温度计的含背景辐射影响的输出信号为

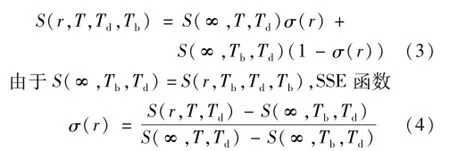
对于不能直接使用上述方法的以温度数字输出或以温度线性化模拟输出的辐射温度计，或可根据分度公式计算温度测量结果的辐射温度计，可利用在数学上等价的虚拟探测器温度SSE计算模型

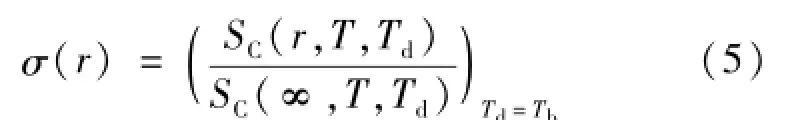
式中，SC为用温度示值T计算的辐射温度计输出信号。它与实测输出信号S服从相同规律。

受辐射源尺寸限制，在实际测量中常以可实现的最大半径rmax作为参照半径。此时，对半径为r的辐射源的SSE函数

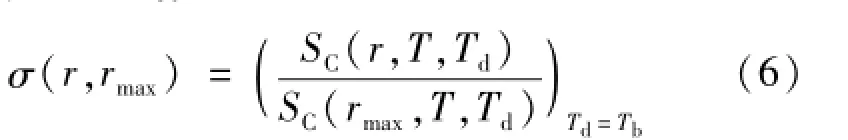
式（5）和式（6）的物理基础为，在虚拟的探测器温度Td＝Tb条件下，探测器与背景处于辐射平衡状态，相互辐射净交换为零，不需考虑背景辐射的影响。它适用于远离背景温度的任意源温度下的SSE测量。与文献［6，8］中的低温测量SSE计算公式相比在数学上等价，但式（6）避免了计算公式中出现无限大辐射源项，在形式上更简明地表达测量模型的物理意义。

在可认为Td、Tb均为0 K的高温测量时，式（6）简化为

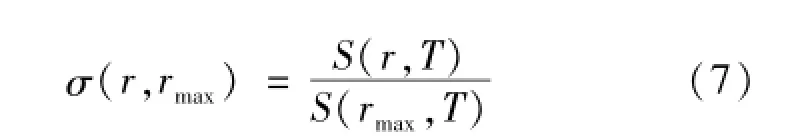
与经典文献中的高温测量SSE函数相同。

2.2 以温度示值增量表示的SSE函数

对于温度数显或温度线性化输出的辐射温度计，其SSE的测量结果只能根据温度示值推算其探测器输出信号。由于SSE的影响，辐射源半径由rmax至r的变化对辐射温度计温度示值T的变化为ΔTSSE（r，rmax）时，以ΔTSSE表示的SSE函数为

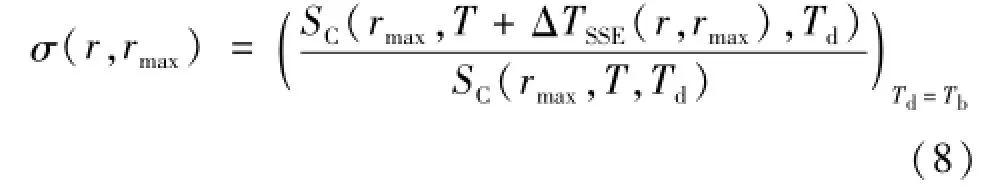
以ΔTSSE（r，rmax）为参数的SSE表示方法，可直观表达SSE对温度测量示值的影响。但ΔTSSE不仅是辐射源尺寸和温度计特性的函数，也是辐射源温度的强函数，即ΔTSSE（rmax，σ（r，rmax），R（λ），T）。当辐射温度计发射率设置［5］不为1时，它还是发射率设置和环境温度的函数，给不同测温条件下的SSE特性的比较和修正带来困难。采用式（8）可以得到不依赖于具体被测温度的SSE表示，便于不同温度下的SSE修正计算与不同测量条件和不同温度计之间的SSE特性比较。

2.3 辐射温度计的SSE计算方法

对于输出信号与入射辐射通量成正比的辐射温度计，可直接根据式（5）或式（6）测量瞄准不同半径的辐射源时的输出并计算SSE函数。

以下讨论温度数字显示或温度线性化输出辐射温度计的SSE的计算方法。

为简化数学表达与计算，将窄波段辐射温度计视为单色辐射温度计，或对辐射温度计引入极限等效波长（亦可称极限有效波长）［18］的概念，结合式（1）和式（5）表示的虚拟探测器温度下的辐射温度计输出可简化为

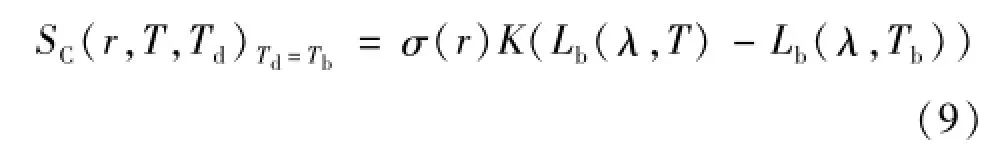
式中，K为仪表系数；λ为辐射温度计的等效波长或近似取为中心波长。

根据式（9），与式（6）对应的SSE计算式为

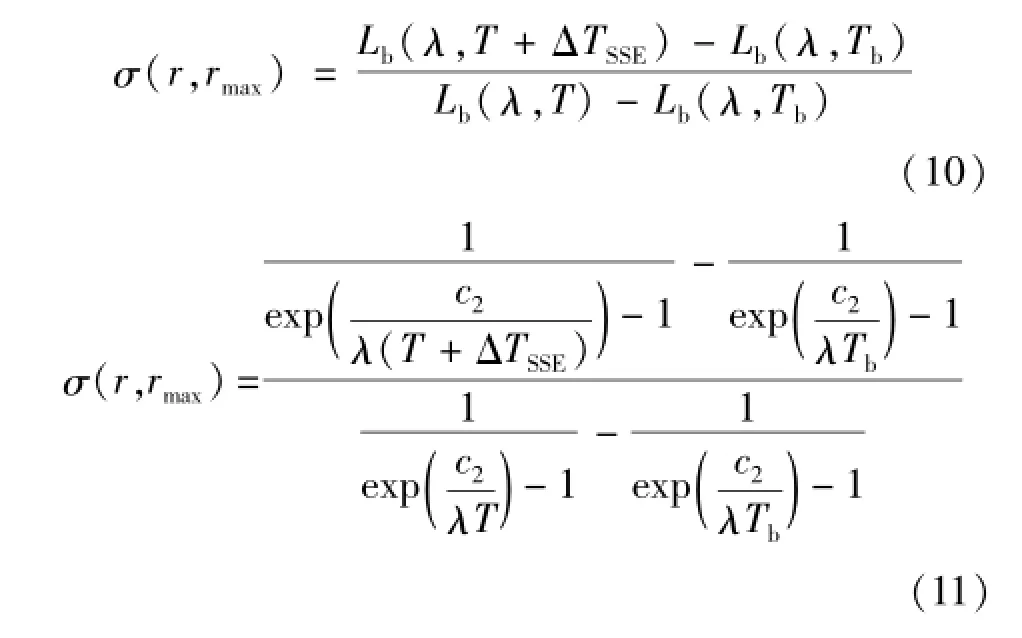
当环境辐射亮度与背景辐射亮度相同时，式（11）也适用于仪表发射率不为1的SSE函数计算［17］，即SSE函数测量结果与辐射温度计的仪表发射率设定值无关。

3 SSE函数性质

两半径之间的SSE函数值与各自SSE函数的参考半径无关

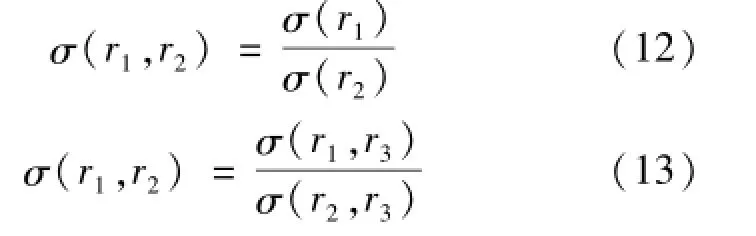
即同一辐射温度计的不同参考半径下的SSE函数是辐射温度计光学系统的同一SSE特性的不同表示形式。

SSE函数值只反映源尺寸效应，与背景温度无关

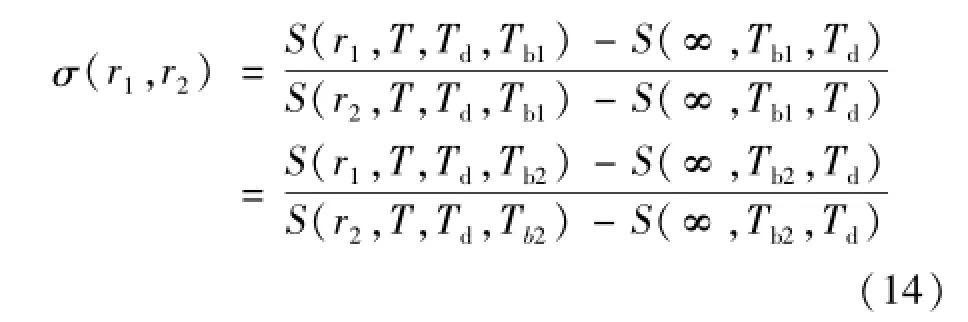
4 典型SSE测量结果

对8～14μm数显辐射温度计Raytek MX4 DCI的SSE测量结果［19］见图1。

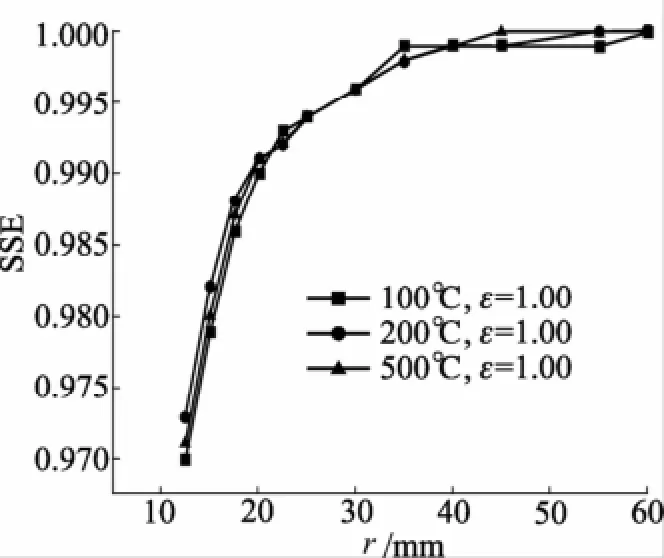
图1 SSE测量结果

5 测温结果的SSE修正

5.1 不同源尺寸与背景温度下的探测器输出信号修正

实际测温中，为测量结果间的比较，需要将不同条件下的测量结果修正到同一测量条件。将测量结果从测量条件1（r1，T，Tb1）修正到测量条件2（r2，T，Tb2）时，修正公式为

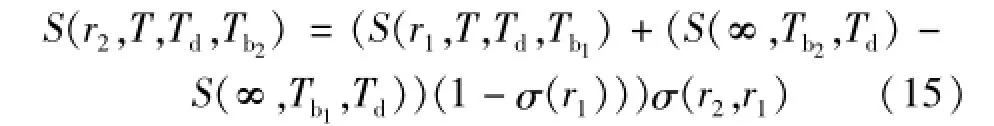
式（15）与文献［6］推导的公式相似，但式（15）是未忽略二阶项的准确公式。实际应用中可能用σ（r1，rmax）近似替代σ（r1）。

5.2 不同源尺寸下的温度示值修正

式（15）信号对辐射温度计示值的影响包含源尺寸变化和背景温度变化2部分。

当2种测量条件的背景辐射差异的影响可忽略时，仅考虑源尺寸因素。同样地，利用上文提出的与背景辐射平衡的虚拟探测器温度的SSE计算方法，修正公式简化为源尺寸变化对温度示值的影响为

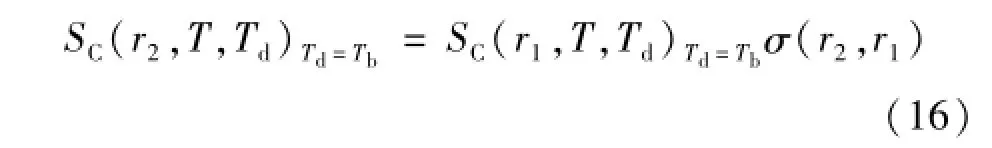
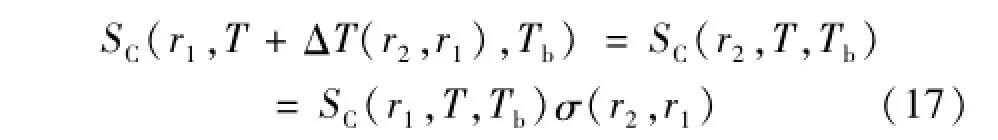
考虑了探测器温度对测温模型的影响，直接利用式（9）带入式（17）计算ΔTSSE（r2，r1）

也可利用式（17）的微分形式计算不同源半径对辐射温度计示值的影响

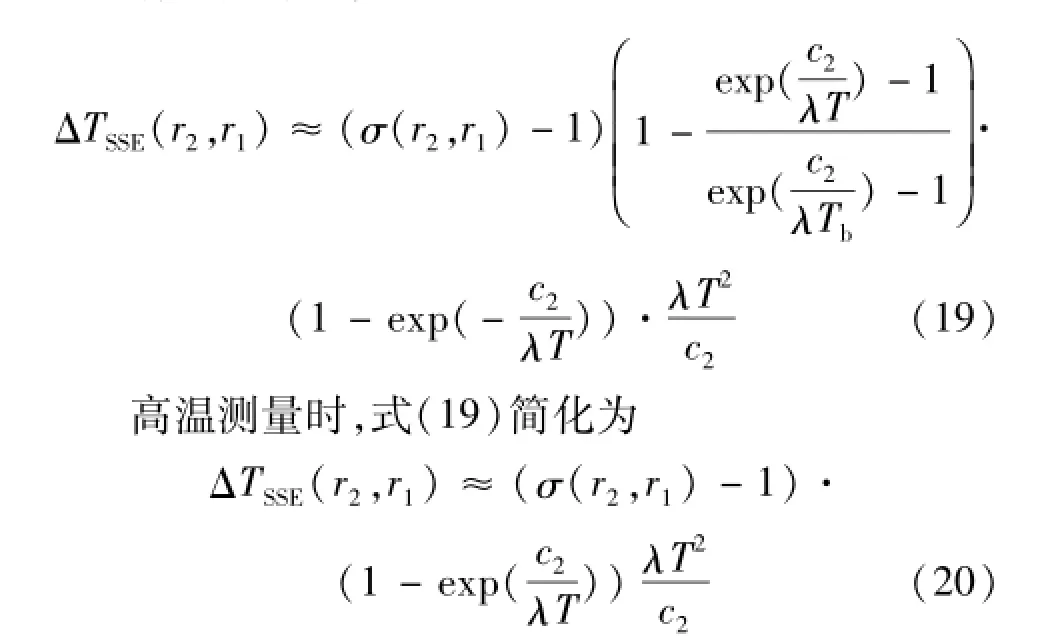
由式（19）、（20）可知，SSE影响具有近似与测温波长和温度平方成正比的因子项。式（20）相对于式（21）多出一个指数比因子项，它在T＝Tb时过零，两侧异号；当T≫Tb时随T增加而趋于1；T＜Tb时，T的指数项随温度降低特别是随波长的测温减小迅速增大。

图2为在背景温度为20℃、SSE影响为0.01时，对波长分别为10μm、4μm和1.5μm的辐射温度计温度示值的影响。图例为波长，部分图例括号中的HT表示用忽略背景辐射的高温测量模型的计算结果。

图2 SSE影响为0.01时对不同测温波长的示值影响

以第4节所述辐射温度计为例，校准时采用直径为50 mm黑体辐射源，在背景温度20℃时测量直径约为80 mm的目标的示值分别为603.1℃、201.2℃和－40.0℃。根据图1查出σ（40 mm，25 mm）＝0.998／0.994，极限等效波长近似取10 μm［18］，则由于测温条件下源半径大于校准源半径，利用式（18），修正SSE对温度示值的影响后的测量结果见表1。

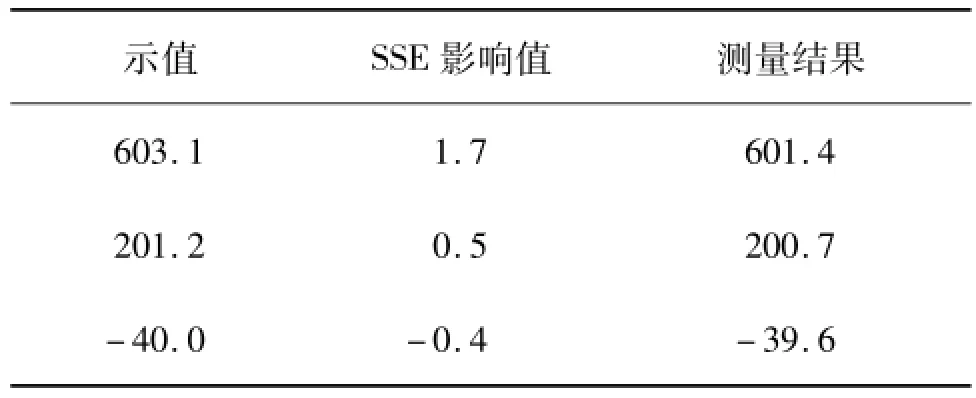
表1 测量目标直径不同于校准结果的修正℃

6 结 论

对单一波段辐射温度计，采用了与背景辐射亮度温度平衡的虚拟探测器温度条件下SSE函数的计算模型，推导了在不同源尺寸和不同背景条件下辐射温度计输出的SSE影响修正的一般性表达式，在利用包含探测器温度影响的测温模型的基础上获得不同源尺寸条件下辐射温度计温度示值的SSE影响修正的简明的解析表达式。

以往的SSE修正文献，在低温应用中，基于忽略探测器温度影响的高温测温模型，必须在测温修正中额外增加背景辐射修正项。本文利用等于背景辐射温度的虚拟探测器温度条件下的测温模型进行SSE对测温的影响修正，消除了背景辐射影响；并利用极限等效波长简化公式形式，得到基于普朗克公式的理论解析表达式，可简明地分析SSE对测温影响的规律。

在低于或接近背景温度（通常接近于环境温度）的低温测量中，SSE的影响显著有别于由高温修正公式得到的结果。对于忽略探测器热辐射和背景辐射影响的高温测量模型，源面积的增加引起的SSE，总是使得测温示值增加，增加幅度与温度平方和测温波长均近似成正比。对于不能忽略探测器热辐射和背景辐射影响的通用测温模型，源面积的增加引起的SSE，对等于背景温度的辐射源的测量结果的影响量为零；随着源温度的提高和波长的增加，影响量升高，高温测量模型的计算值与其趋近；但在长波趋近速度很慢，如采用高温修正公式，即使温度达到300℃，对4μm辐射温度计仅存在1.3%的偏差，对10μm辐射温度计偏差仍达17.6%；低于背景温度时，影响量为负，并且绝对值随温度降低和波长的减小迅速增大。

由于源尺寸对测量结果有显著影响，辐射温度计的检定与校准需要注明实验的源尺寸条件。测温应用中，被测对象尺寸与检定或校准条件有明显差异时，需要修正SSE对测温结果的影响。在较低温度测量的SSE修正公式不同于以往的高温测量修正公式。

［1］ Bloembergen P，Duan Y，Bosma R，etal.The characterisation of radiation thermometers subject to the size-of-source effect［C］／／Proceedings of TEMPMEKO＇96，the 6th International Symposium on Temperature and Thermal Measurements in Industry and Science，Turin，1996.

［2］ 段宇宁，赵琪，原遵东，等.辐射源尺寸效应研究［J］.计量学报，1996，17（3）：161－166.

［3］ Fischer J，Battuello M，Sad Ie M.Uncertainty budgets for realization of ITS-90 by radiation thermometry［C］／／AIP Conference Proceedings，Chicago，USA，2002.

［4］ Saunders P，Fischer J，SadliM.Uncertainty budgets for calibration of radiation thermometers below the silver point［J］.IntJThermophys，2008，29（3）：1066－1083.

［5］ IEC／TS 62492-1 2008-04，Industrial process control devices-Radiation thermometer-Part 1：Technical data for radiation thermometers［S］.

［6］ Bloembergen P.On the correction for the size-of-source effect corrupted by background radiation［C］／／Proceedings of TEMPMEKO 1999，the 7th International Symposium on Temperature and Thermal Measurements in Industry and Science，Delft，1999.

［7］ Machin G，Ibrahim M.Size-of-source effect and temperature uncertainty：I-high temperature systems［C］／／Proceedings of TEMPMEKO 1999，the 7th International Symposium on Temperature and Thermal Measurements in Industry and Science，Delft，1999.

［8］ Saunders P，Edgar H.On the characterization and correction of the size-of-source effect in radiation thermometers［J］.Metrologia，2009，46（1）：62－74.

［9］ Machin G，Ibrahim M.Size-of-source effect and temperature uncertainty：II-low temperature systems［C］／／Proceedings of TEMPMEKO 1999，the 7th International Symposium on Temperature and Thermal Measurements in Industry and Science，Delft，1999.

［10］ Yoon H W，Allen D W，Saunders R D.Methods to reduce the size-of-source effect in radiometers［J］.Metrologia，2005，42（2）：89－96.

［11］ Bloembergen P.Analytical representations of the size-ofsource effect［J］.Metrologia，2009，46（5）：534－543.

［12］ Saunders P.Correcting Radiation Thermometry Measurements for the Size-of-Source Effect［J］.IntJ Thermophys，2011，32（7－8）：1633－1654.

［13］ LU X F，YUAN ZD，LIU J，etal.Study on the Sizeof-Source Effect due to Objective Lens of Radiation Thermometer［J］.计量学报，2008，29（5A）：146－149.

［14］ 卢小丰，原遵东.孔径光阑对辐射源尺寸效应的影响研究［J］.计量技术，2010，（7）：3－5.

［15］ Yuan Z，Lu X，Wang J，etal.Realization of ITS-90 Above the Silver Point at the NIM［J］.IntJ Thermophys，2011，32（7－8）：1611－1621.

［16］ Hao X，Yuan Z，Lu X，etal.Size-of-Source Effect Difference Between Direct and Indirect Methods of Radiation Thermometers［J］.IntJThermophys，2011，32（7－8）：1655－1663.

［17］ 原遵东.消除背景辐射影响的辐射源尺寸效应测量模型［J］.光学学报，2011，31（12）：1212002.

［18］ 原遵东.辐射温度计的等效波长及其应用［J］.仪器仪表学报，2009，30（2）：374－379.

［19］ 郭莉莉，原遵东，邢波，等.工业辐射温度计的辐射源尺寸效应（SSE）测量［J］.计量技术，2010，（9）：6－9.

Size-of-source Effect Correction for Infrared Radiation Thermometer

YUN Zun-dong
（National Institute of Metrology，Beijing 100013，China）

The feature of the size-of-source effect（SSE）in low temperature measurement differs from that in high temperaturemeasurement.A correction formula for the SSE in different source sizes and different background radiations is derived.It is from a calculation model at a suppositional detector temperature which can avoid the influence of background radiation on the SSE measurement.Theoretical analytical expression for the SSE in different source sizes are obtained，and the rule of the novelmodel and classical high temperaturemodel are different at the source temperature lower than or near ambient temperature.The formulae and conclusion are suitable for the SSE correction for a temperaturemeasurement at an arbitrary temperature.

Metrology；Size-of-source effect；Suppositional detector temperature；Background radiation；Radiation thermometer；Temperature correction

TB942

A

1000-1158（2014）01-0005-05

10．3969／j．issn．1000-1158．2014．01．02

2011-10-27；

2012-12-05

原遵东（1960－），福建莆田人，中国计量科学研究院研究员，主要研究方向为温度计量。yuanzd＠nim.ac.cn