线结构光双目传感器钢坯轮廓测量标定方法

万聪灵， 余学才， 蒋 波， 李泽思

（电子科技大学光电信息学院，四川成都 610054）

线结构光双目传感器钢坯轮廓测量标定方法

万聪灵， 余学才， 蒋 波， 李泽思

（电子科技大学光电信息学院，四川成都 610054）

针对现有线结构光轮廓尺度测量系统标定方法对环境要求高、设备昂贵、标定过程复杂等问题，提出了一种基于网格平面标定板的现场标定方法。该方法主要特点是不需要复杂的标定模型和高精度的辅助设备，只需要将2 mm宽和高的矩阵状标定板置于需要测量区域，通过角点检测求出基于同一个世界坐标系的标定参数，并完成对双目摄像机标定系统误差校正，最后把测量系统统一到一个图像坐标系。该标定方法应用于钢坯轮廓尺度测量中，实测数据表明其具有较强的鲁棒性和可行性，测量误差为0.05 mm。

计量学；线结构光；双目摄像机；尺度测量；标定方法

1 引 言

近十几年研发的基于机器视觉轮廓尺度测量技术具有高速、高分辨率、非接触、易于管理数据等优点，能够实现系统在线实时测量［1～3］。基于机器视觉的线结构光法（光切法），是指激光器发射的激光束通过鲍威尔棱镜产生密度均匀的扇形激光面照射到被测物体表面产生一条明亮的光带，通过摄像机采集获得数字图像，经图像运算获得物体表面二维轮廓。为了获得360°的完整轮廓，需要使用多个图像传感器从多个方向获取物体部分轮廓，将所有图像传感器获取的轮廓融合，获得完整的轮廓图。多图像传感器图像标定技术是三维轮廓测量的重要环节，决定系统的测量精度［4，5］。

有关多摄像机标定技术，国内外均有一些研究。哈佛大学Yau ST教授等提出在基于摄像机和投影仪线性模型内、外参数双目摄像机标定方法［6］。四川大学苏显渝教授等提出了一种基于摄像机内、外参数标定方法［7］，该方法通过特征点求出线结构光平面方程，最后通过旋转平移矩阵进行空间图像坐标系的统一，该方法对标定板的位置要求不强，位置可以任意。西安交通大学的赵宏教授等提出了一种基于摄像机直接线性变换模型求解系统参数［8，9］，该方法运用插值方法求解靶标特征点之间未知点的世界坐标方法，再运用统一的特征参考点完成多摄像机之间的空间图像坐标系的统一，最后提出基于线结构光面调节向标定面重合的误差校正方法，但需要高精度的二维平台进行重合调节，线结构光面x方向与y方向调节时必须保证相互独立，难度较大。上述这些标定方法标定步骤繁琐，需要加工精密辅助设备，运用在高温、高湿度和高抖动等这些恶劣条件的热轧钢坯测量有一定的局限性。

本文提出一种基于图像旋转平移的误差校正标定方法，通过采用空间标定板统一的特征点作为两图像坐标系参考点进行单摄像机标定，最后利用圆型工件在测量空间内自由移动求出系统的误差校正参数，从而完成整个测量系统的标定。该标定方法不需要高精度的辅助设备，步骤简单，效率高，摄像机标定方法选取灵活。

2 测量系统

2.1 系统结构

线结构光轮廓尺度测量系统如图1所示。系统主要由两个灰度红外摄像机及其三维调节平台、3个线结构激光光源及其二维调节平台和系统结构固定架组成。摄像机1和2通过三维平台调整到水平等高位置固定，其光轴相交于测量区域的中心点。调整线结构激光光源1、2和3二维平台使激光光面共面，且平行与摄像机1和2的共面平面，考虑到系统测量的高温钢坯的光谱特性，选择波长808 nm近红外的激光光源。

在系统测量时，钢坯被限定在标定区域内，以垂直于激光光面向着摄像机1和2所在的平面垂直方向运动，此时线结构光源会在钢坯表面形成光切面，通过两个摄像机采集图像运算，可计算钢坯的一系列轮廓尺度数据。

图1 线结构光轮廓尺度测量系统

2.2 双目摄像机结构

图2为线结构光双目摄像机的针孔透视成像示意图。O1和O2分别为摄像机1和2的光心，OwXwYwZw为线结构光平面空间世界坐标系，Zw轴为钢坯行进方向。Oc1Xc1Yc1Zc1和Oc2Xc2Yc2Zc2为摄像机1、2的空间相机坐标系，Zc1和Zc2轴分别与摄像机1和摄像机2光轴重合，相交于Ow点。O1U1V1和O2U2V2为摄像机1、2的空间图像坐标系，U1轴和V1轴与Xc1轴和Yc1轴平行，摄像机2也是如此。P点为在线结构光平面内的轮廓点，P1和P2表示为对应在摄像机1和摄像机2的像素点。

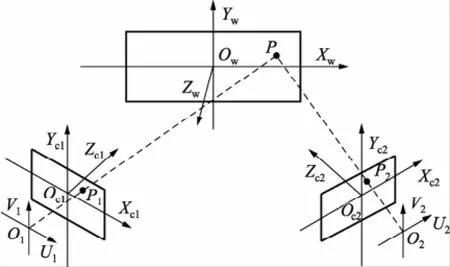
图2 线结构光双目摄像机结构

3 轮廓测量标定方法

所提出的钢坯轮廓尺度测量标定方法主要分为两大部分：摄像机的标定和系统标定误差的校正。在双目摄像机测量系统中，双目摄像机所能分别获取轮廓的左、右光带图像，而两幅图像之间重叠的区域非常少，且在实测过程中会存在遮挡的现象，因此摄像机的标定方法必须采取单独标定。系统标定误差的校正，多摄像机标定过程中的标定误差主要是由于摄像机标定面和单像素轮廓面不共面引起的，本文提出一种基于图像旋转平移的误差校正方法，它主要是利用标定还原后的图像的圆心坐标差来校正系统标定误差，因此在摄像机标定方法选取上较灵活，可以根据不同的需求选取不同的摄像机标定方法。

3.1 双目摄像机标定方法

提出一种隐参数标定方法进行单个摄像机标定。通过图像处理获取空间矩阵标定板上的指定特征点的图像坐标，其中特征点的世界坐标已知，并置于标定程序内自动完成标定参数的计算。测量系统中两个摄像机空间图像坐标系的统一是图像数据融合的基础，因此在单个摄像机标定过程中采取统一的标定板世界坐标系，以保证系统测量精度的一致性。在实际定标过程中，为了提高图像数据的融合精度，选取双目摄像机有效测量范围内统一的特征点作为参考点。

待摄像机和线结构光调整固定之后，再把矩阵标定板置于线结构光平面测量区域内，在整个操作过程中要尽量保证矩阵标定板与线结构光平面完全重合并固定。此时摄像机1和2能够分别获取矩阵标定板的图像，再通过角点检测求出统一参考点的图像坐标。从图像坐标系到世界坐标系的变换需经过旋转平移及仿射投影变换，考虑到图像的畸变效应，其映射关系为：

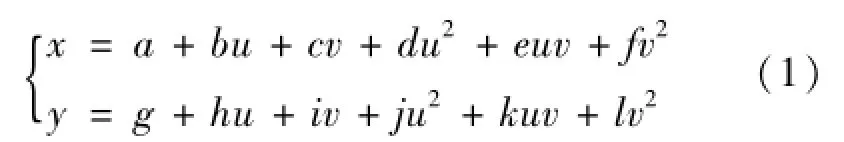
其中：（x，y）表示世界坐标中的某一个特征点坐标，mm；（u，v）表示对应空间图像坐标系中的坐标，pixel；a、b、c、d、e、f、g、h、i、j、k、l为待定标定系数，即隐参数。一旦标定系数确定，图像中任意一点的世界坐标系可以按公式（1）进行计算。在这里为了能够提高标定精度，一般在矩阵标定板上均匀分布选取33个特征点作为参考点。利用这些已知特征点的图像坐标和世界坐标，采取最小二乘法解超定方程组，求出标定参数。

当选取了33个特征点的世界坐标后，相应的33个特征点的图像坐标可以构造矩阵A：

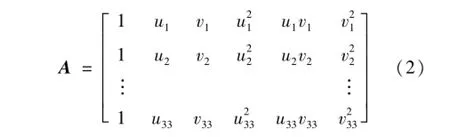
33个特征点的x坐标可构造矩阵B：

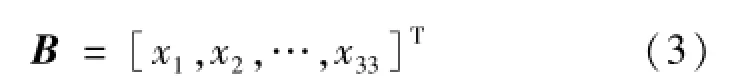
而剩下的6个待定系数可构造矩阵C：

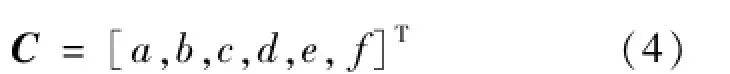
由最小二乘法矩阵运算可得：

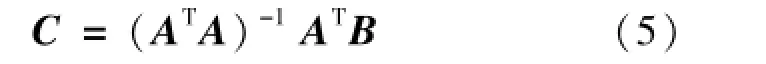
同理，如上构造矩阵求解方程（2）的6个待定系数，最后可获得标定图像的12个待定系数。通过上述方法分别完成摄像机1和2的标定，得到测量系统的24个标定参数。

3.2 系统标定误差校正方法

由于摄像机1和摄像机2标定过程中，标定板采用的是统一的空间世界坐标系，因此对还原之后的图像1和2的图像数据可以直接进行相加融合，从而获得融合后的光切面的二维轮廓图像，避免了采取复杂的传统图像匹配融合技术。

在对融合后的二维轮廓图像尺度数据分析发现相交于真实的光切面轮廓尺度数据，融合后的图像轮廓尺度测量数据存在一定的失真，失真原因主要是摄像机获取轮廓光带图像后，需要经过二值化、细化、中心提取形成一条单像素轮廓图像，再对单像素轮廓数据进行图像还原，获得光切面的非畸变轮廓图像。在经过上述一系列步骤之后，无法保证单像素轮廓面与标定面属于同一个平面，从而造成融图像轮廓数据失真。当标定面在单像素轮廓面前面时，图像轮廓测量尺度数据偏大，当标定面在单像素轮廓面后面时，图像轮廓测量尺度数据偏小。

针对上述问题，提出一种基于图像旋转平移的标定误差校正方法，它主要是采取以摄像机1和2分别获取标准圆型工件的左、右光切面轮廓图像，然后通过图像预处理，再分别对图像1和2进行标定还原获得非畸变的光切面轮廓图像，最后通过圆心拟合算法分别求出左、右非畸变轮廓图像在统一图像坐标系中各自的圆心坐标，并记录下轮廓圆心坐标之差的数据从而求出系统的拟合误差校正系数，根据公式（6）：

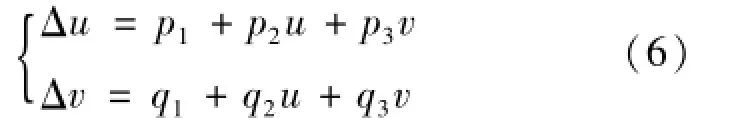
式中：（u，v）表示为圆型工件非畸变轮廓图像2中的圆心坐标，在这里采取以摄像机1的图像坐标为参考坐标进行图像坐标系的统一；（Δu，Δv）表示圆型工件非畸变图像1和2的圆心坐标之差；p1、p2、p3、q1、q2、q3表示待定误差校正系数。通过合理的区域划分，只需把圆形工件任意放置在6个测量位置，利用公式（6）就可以求出相应6个待定系数。

待待定系数确定之后，通过图像预处理和标定还原过程分别获得非畸变左、右轮廓图像1和2，此时由圆心拟合算法求出右轮廓非畸变图像2的圆心坐标（u0，v0），再把坐标点（u0，v0）代入公式（6）可以确定该帧图像的补偿坐标误差（Δu0，Δv0），最后把坐标误差（Δu0，Δv0）反向补偿到融合后的图像中，从而完成测量系统的误差校正。为了提高拟合后数据的精度，在实测过程中，采取对图像进行25块均匀划分，分别获取圆型工件在每块区域的圆心坐标之差进行数据拟合，拟合系数求解类似于隐参数求解过程，这里不再叙述。

4 实验及结果

为了使摄像机标定有更高的精度，专门制作了一块高精度的标定板。如图3所示，标定板面积100 mm×48 mm，靶上密排2 mm×2 mm大小的正方形网格线，每一个网格的十字交叉线为特征参考点。该测量系统的测量有效范围为激光光平面内60 mm×48 mm的范围。

图3 摄像机2获取的标定板图像

在整个系统的标定过程中，首先把标定板置于线结构光平面内，摄像机1和2分别获取标定板在各自测量角度上的畸变图像，见图3。通过角点检测求出标定图像中的十字角点，并筛选出已知的33个参考点在相应图像中的位置（图3中“×形”点为特征参考点的对应图像点，采取的标定板左下角为统一的世界坐标系原点），通过公式（1）分别求出摄像机1和2各自的12个标定系数，标定参数如表1和表2所示，并把标定图像进行还原验证。

表1 摄像机1的12个标定系数mm／pixel

表2 摄像机2的12个标定系数mm／pixel

在求出测量系统24个标定参数后，把标定参数输入到事先已经设计好的标定误差校正程序中。此时为了能够获得较为理想的误差校正效果，用一个直径20 mm的圆型工件在测量区域内游走并记录下圆心坐标差（Δu，Δv），图4为误差校正前左、右轮廓非畸变图像1和2的融合图像，其中O1表示图像1轮廓的拟合坐标圆心，O2表示图像2轮廓的拟合坐标圆心。再从记录下的圆心坐标误差中，筛选出均匀分布的25不同位置的圆心坐标误差值，代入公式（6），用最小二乘法求出拟合系数，见表3。图5表示误差校正后圆型工件左、右轮廓合成融合图像，圆心坐标误差控制在1个像素以内。

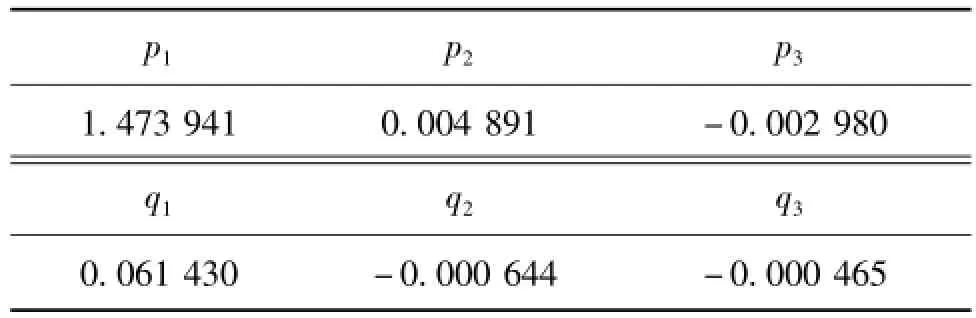
表3 系统误差校正系数mm

图4 误差校正前的测量系统圆型工件融合图

为了进一步验证实验结果，运用这套系统对某钢铁公司生产的热轧圆型钢坯进行检测，其中圆钢检测的A、B、C和D这4个尺度参数均采用圆钢尺度检测标准定义值，表4所示分别表示精确游标卡

图5 误差校正后的测量系统圆型工件融合图

尺和图像测量系统所测圆钢4个尺度参数值。实验表明该系统误差校正后的测量误差为0.05 mm，该方法完全能够满足工业测量的要求。

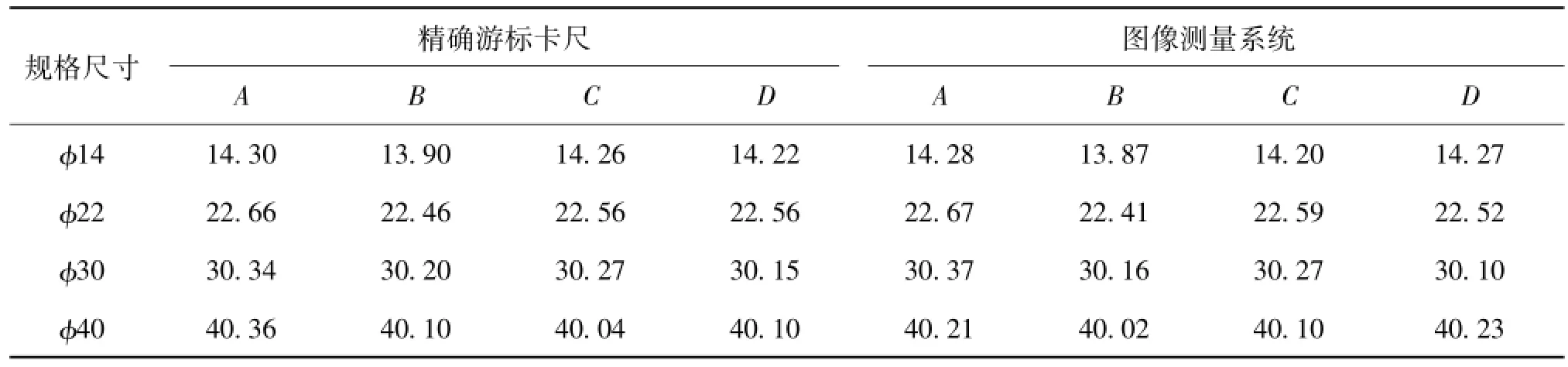
表4 精确游标卡尺和图像测量系统所测圆钢4个尺度参数值mm

5 结 论

本文提出的钢坯轮廓尺度测量标定方法，主要采用基于统一世界坐标系的标定板进行单摄像机标定，并利用圆型工件建立起圆心坐标位置与标定误差的函数关系式，该方法无需辅助调整设备，标定速度快，效率高和鲁棒性强，有利于机器视觉测量系统在工业检测中应用。在整个测量系统标定过程中，虽然误差校正能够校正系统标定误差，但是标定面与线结构光面的重合度决定整个系统的标定精度，因此在激光器的选择上不宜选择发散角较大的激光器。此外钢坯轮廓测量系统使用了锁定成像技术，用于消除背景光，钢坯散发的红光和CCD的暗电流影响。根据该方法开发的一套标定软件能够现场完成摄像机的标定和系统误差校正，并自动生成标定参数和误差校正参数。

［1］ Chen Frank，Brown G M，Song Mumin.Overview of three dimensional shape measurement using optical methods［J］.OptEng，2000，39（1）：10－22.

［2］ 王学影，刘书桂，张洪涛，杜建军.基于参数分离机器人手眼视觉标定方法研究［J］.计量学报，2007，28（2）：106－109.

［3］ 张洪涛，段发阶，等.基于两步法线阵CCD标定技术研究［J］.计量学报，2007，28（4）：311－313.

［4］ 贾波，苏显渝，郭履容.采用激光光刀的叶片三维面形测量方法［J］.中国激光，1992，A19（4）：271－275.

［5］ Chen X B，Xi J T，Ye Jin.Accurate calibration for a camera projectormeasurement system based on structured light projection［J］.Opt＆LasersinEnging，2009，47（34）：310－319.

［6］ Zhang S，Yau S T.Three－dimensional shape measurement using a structured light system with dual cameras［J］.OptEng，2008，47（1）：1－12.

［7］ 吴庆阳，苏显渝，向立群，李勇.线结构光双传感器测量系统的标定方法［J］.中国激光，2007，34（2）：259－264.

［8］ 张维光，赵宏，张琦，周翔.线结构光三维轮廓测量系统的标定方法［J］.中国激光，2009，36（1）：180－188.

［9］ 张维光，赵宏.线结构光多传感器三维测量系统误差校正方法［J］.西安交通大学学报，2011，45（6）：75－80.

Calibration Method for Billet Outline Dim ension Measurem ent Using Linear-structure Lightw ith Two-senor

WAN Cong-ling， YU Xue-cai， JIANG Bo， LIZe-si
（School of Optoelectronic Information，UESTC，Chengdu，Sichuan 610054，China）

To solve the calibration problems in the dimensionmeasurementbased on linear-structure light such as high requirement of environment，comp licate calibration procedure and so on，a calibration method based on the grid panel has been presented.Its main advantage is that，rather than a complicated calibration model and high precision auxiliary equipment，only a calibration planewith 2mm width and heightatmeasurementplace isneeded.With corner-detection，the calibration parameters based on a global world coordinate can calculated，the revising system error correction was comp leted，and finally themeasurement system into the image coordinate system wasmerged.The calibration method has been applied in billet outline dimension measurement and the experimental data shows that the method has stronger robustness and feasibility with the error of 0.05mm.

Metrology；Linear-structure light；Dual camera；Dimension measurement；Calibration method

TB92

A

1000-1158（2014）01-0034-05

10．3969／j．issn．1000-1158．2014．01．08

2013-05-21；

2013-06-24

贵阳市科技局资助项目（20121014－29）

万聪灵（1987－），男，江西九江人，电子科技大学硕士研究生，主要研究方向是工业图像处理、机器视觉和模式识别。wcl1987luck＠163.com