带3-分片NCP函数的无罚函数和滤子的SQP算法

周 敏，尚有林

（河南科技大学数学与统计学院，河南 洛阳 471023）

带3-分片NCP函数的无罚函数和滤子的SQP算法

周 敏，尚有林

（河南科技大学数学与统计学院，河南 洛阳 471023）

对于非线性约束优化问题，提出了一种新的无罚函数和滤子的SQP算法。根据优化问题的一阶KKT条件，利用乘子和3-分片NCP函数，得到非光滑方程以致简化优化问题。在线搜索的过程中，采用无罚函数和滤子的方法。同时证明了该SQP算法是可行的，并具有全局收敛性。

滤子；SQP算法；收敛；NCP函数

0 引言

考虑如下的约束非线性规划问题（NLP）：

其中，x∈ℝn，f：ℝn→ℝ，Ci：ℝn→ℝ，都是二次连续可微函数。

非线性规划问题（NLP）的拉格朗日函数为：

其中，λ＝（λ1，…，λm）T∈ℝm是乘子向量。

问题（2）是一种非线性互补问题（NCP）。由于NCP函数的各种性质引起了广泛的关注，一个解决非线性互补问题（2）的方法是构建一个可求解的非线性方程：Φ（x，λ）＝0。为了避免实际问题中惩罚参数的设置，Fletcher第一次提出了关于求解约束非线性优化问题的滤子方法［1］，同时定义了约束违反度函数

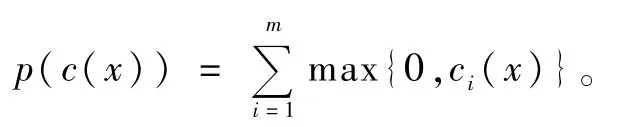
Gould和Toint提出了一种新的无罚函数和滤子的方法，这个方法被证明是全局收敛性的，并用于SQP方法或信赖域SQP方法关于非线性等式约束问题的求解［2－6］。

本文对于非线性约束优化问题，提出了一种新的无罚函数和滤子的SQP算法。根据优化问题的一阶KKT条件，利用乘子和3-分片NCP函数，得到非光滑方程以致简化优化问题。在线搜索的过程中，采用无罚函数和滤子的方法。对给出的新的SQP算法，证明了该算法是可实现的，并进一步讨论了该算法的收敛性。

1 预备知识

定义1函数φ：ℝ2→ℝ，如果有

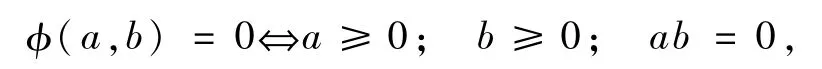
则称φ为一个NCP函数。

较为常用的NCP函数有F-B NCP函数、极小化NCP函数、3-分片线性NCP函数等，对于其他的NCP函数及其性质，见文献［7－8］。

本文采用3-分片线性NCP函数来求解，形式如下：

式中，φ是除原点外处处可微函数，但是在原点处是强半光滑。

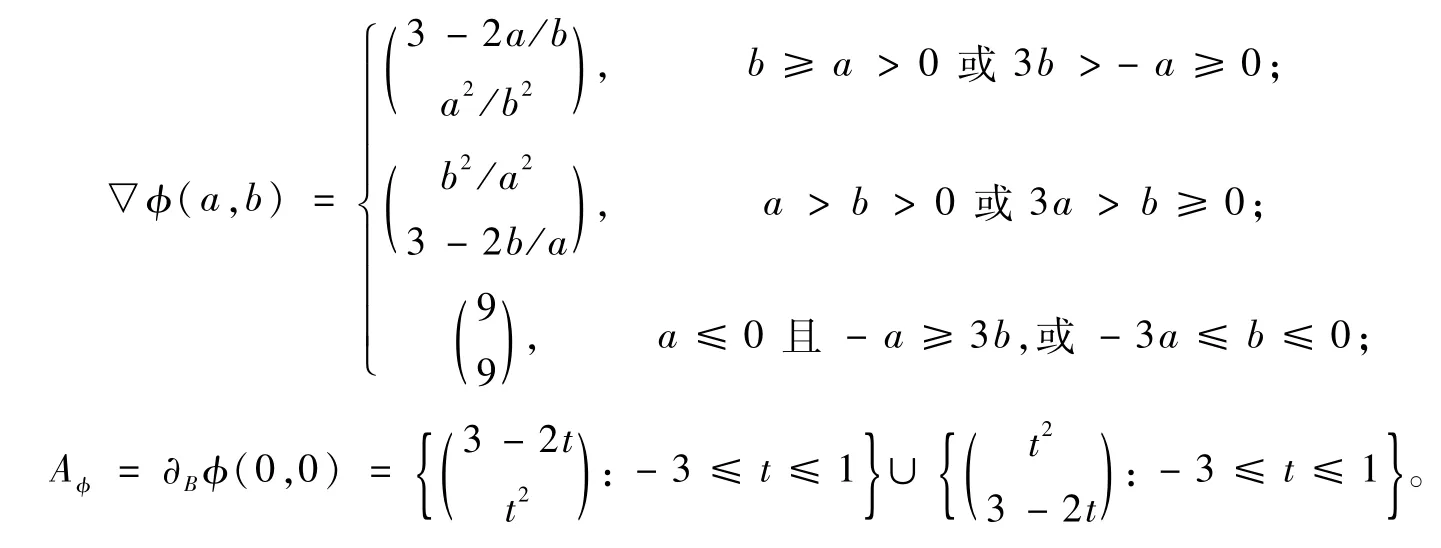
为了充分利用NCP函数与KKT条件间的关系和NCP函数几乎处处可微的性质，本文改造滤子中的度量，将约束违反度函数p（x）修正为：

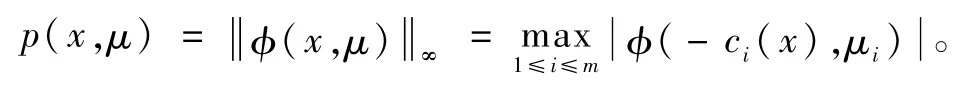
对于一个给定的迭代点xk∈ℝn，即问题（NLP）的局部最优解xk的当前估计，解如下问题QP（xk，d）得dk（同时可以得到问题QP（xk，d）对应的乘子λk），

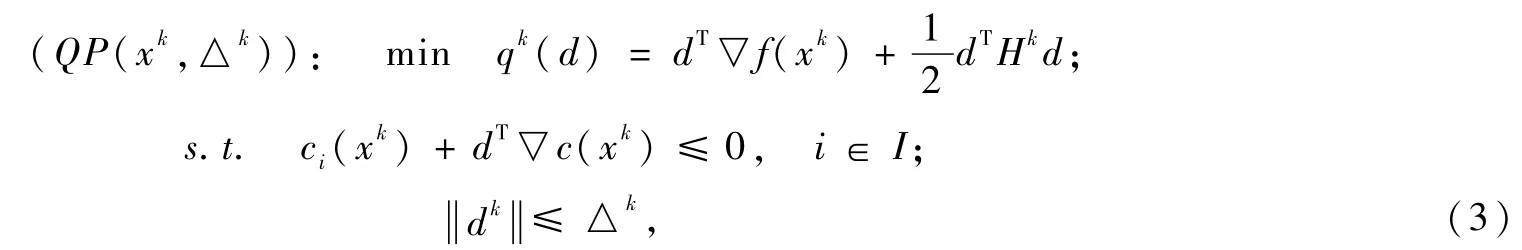
其中，Hk是拉格朗日函数的近似Hessian阵表示欧几里得范数。

函数f（xk）的真实下降量

f（xk）的预测下降量

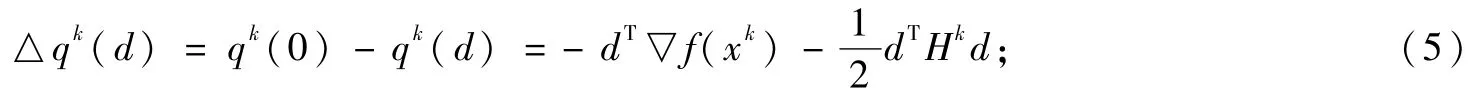
f（xk）的充分下降条件表示为：

其中，τ是某一个常数。

选择xk＋1为下一个迭代点，则xk＋1满足

需要指出的是，若xk＋dk不满足式（7）～式（9），但是却很接近最优解，即出现了所谓的Maratos效应，为了克服此现象，计算二阶校正步（SOC），即解决如下子问题

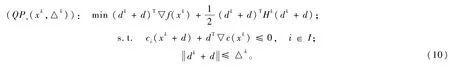
2 新的SQP算法

2.1 S0：初始化

2.2 S1：计算QP（xk，△k）

S1.1 如果QP（xk，△k）是不可行的，进入恢复性阶段，找到一个点xk＋1，直至使QP（xk＋1，△k＋1）可行，返回S1；

S1.2 如果QP（xk，△k）是可行的，得到dk，置xk＋1＝xk＋dk，进入S2。

2.3 S2：判断终止条件

S2.1 如果dk＝0，停止，得到KKT点xk；

S2.2 如果dk≠0，计算拉格朗日乘子λk，同时计算△f和△q，进入S3。

2.4 S3：无罚函数和滤子的线搜索

S3.1 如果（xk＋1，λk）满足式（7）～式（9），进入S4；

S3.2 如果（xk＋1，λk）不满足式（7）～式（9），计算SOC（QPs（xk，△k）），得到，记，进入S3.3；

S3.3 如果（xk＋1，λk）不满足式（7）～式（9），减小信赖域半径△k＋1和计算QP，返回S1。

2.5 S4：判断充分下降条件

S4.1 如果xk＋1不满足式（4）～式（6），减小信赖域半径△k和计算QP，返回S1；

S4.2 如果xk＋1满足式（4）～式（6），更新信赖域半径△k和Bk＋1。如果xk＋1满足式（7）而xk不满足，则，否则。如果式（7）满足，则，否则置rk＋1＝rk。置k＝ k＋1返回S1。

在算法中，当问题不相容或者信赖域半径小于事先给定的下界时，算法将会进入到恢复阶段。恢复阶段具体算法可以参见文献［1］。

3 收敛性分析

在下面的分析中，需要如下假设：

A1 目标函数f和约束函数ci（x）都是二次连续可微的。

A2 算法产生的所有迭代点均位于一个有界紧凸集S中。

A3 存在正常数a、b，使得Hessian阵Hk满足，∀k和d∈ℝn成立。

A4 子问题QP（xk，△k）的KKT乘子λk一致有界，QPs（xk，△k）的KKT乘子k一致有界。

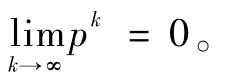
证明根据S2～S4，得到是单调递减并且

由于k≥k1时，｛fk｝是单调递减的，同时式（11）表明当k→∞时，有f（xk）→－∞，这与假设矛盾。

故引理得证。

算法有3个不成功（即xk＋1＝xk）的循环

循环1 S1.2-S2.2-S3.1-S4.1-S1；

循环2 S1.2-S2.2-S3.1-S4.2-S1；

循环3 S1.2-S2.2-S3.2-S3.3-S1。

为了说明算法是有效的，迭代是成功的，即上述的3个循环是有限终止的，给出以下3个引理：

引理2算法中循环1是有限终止的。

引理3算法中循环2是有限终止的。

引理4算法中循环3是有限终止的。

在第2部分新的SQP算法的迭代过程中，xk＋1＝xk＋dk或者xk＋1＝xk＋dk＋k成立，因此，可以看出引理2～引理4是成立的，即第2部分给出的新的SQP算法是可执行的。

由A1～A4是成立的，给出算法的全局收敛性定理。

定理1由算法产生的序列有如下情况：

（Ⅰ）迭代到问题（NLP）的KKT点；

（Ⅱ）至少存在一个聚点是问题（NLP）的KKT点。

该算法的证明类同于文献［9］。

4 结束语

综上所述，本文提出了一种新的无罚函数和滤子的SQP算法，其中该算法是基于3-分片NCP函数。由此类推也可将本文中的方法用于4-分片NCP函数或者其他的NCP函数，继而可得到相似的结论。

［1］ Fletcher R，Leyffer S.Nonlinear Programming Without a Penalty Function［J］.Math Programming，2002，91（2）：239－269.

［2］ Fletcher R，Leyffer S，Toint P.On the Global Convergence of a Filter-SQP Algorithm［J］.SIAM J Optim，2002，12：44－59.

［3］ Panier E R，Tits A L，Herskovits J N.A QP-free，Globally，Locally Superlinear Convergent Method for the Inequality Constrained Optimization Problems［J］.SIAM J Control Optim，1988，36：788－811.

［4］ Pu D，Li K，Xue W.Convergence of QP-free Infeasible Methods for Inequality Optimization Problems［J］.J of Tongji University，2005，33：525－529.

［5］ Liu X，Yuan Y.A Sequential Quqdratic Programming Method a Penalty Function and a Filter for Equality Constrained Nonlinear Programming［J］.SIAM J on Optimization，2011，91：545－571.

［6］ Ulbrich M，Ulbrich S.Non-monotone Trust Region Methods for Nonlinear Equality Constrained Optizization Without a Penalty Function［J］.Math Program，2003，95：103－135.

［7］ Galantai A.Properties and Construction of NCP Functions［J］.Comput Optim Appl，2012，52（3）：805－824.

［8］ Pu D，Zhou Y.Piecewise Linear NCP Function for QP-free Feasible Method［J］.Applied Mathematics，2006，21：289－301.

［9］ Su K.Trust-region Filter Method with NCP Function［J］.Math，2008，28（12）：1525－1534.

O224

A

1672－6871（2014）04－0082－04

国家自然科学基金项目（10971053）；河南省自然科学基金项目（094300510050）

周 敏（1987－），女，河南三门峡人，硕士生；尚有林（1963－），男，河南洛阳人，教授，博士，博士生导师，主要研究方向为非线性规划.

2013－10－29