磁耦合调谐质量阻尼器的参数优化及减振效果

李晓华，王宝基，薛中会

（河南理工大学物理化学学院，河南 焦作 454000）

磁耦合调谐质量阻尼器的参数优化及减振效果

李晓华，王宝基，薛中会

（河南理工大学物理化学学院，河南 焦作 454000）

在调谐质量阻尼器的基础上，将黏性阻尼器换成电磁阻尼器，建立了3个自由度磁耦合调谐质量阻尼系统的力学模型及其运动学方程。利用傅里叶变换导出了该系统随外激励变化的傅里叶响应函数。根据固定点法和参数组合筛选法对系统的参数进行了优化处理，得到了最优频率比、电阻尼比和耦合参数。减振效果显示，磁耦合调谐质量阻尼器比调谐质量阻尼器的减振效果提高了20%左右。

调谐质量阻尼器；磁耦合；参数优化；傅里叶变换

0 引言

目前，为了减轻外激励作用而引起建筑物的振动，许多被动控制器已成功地安装在世界各地的高耸建筑物和塔上，如美国纽约的Citicorp中心，波士顿的John Hancock塔，澳大利亚悉尼Centerpoint塔等。调谐质量阻尼器（TMD）是被动控制器之一，它能使主体结构的振动得到很好的抑制［1－6］。目前，一些研究发现，在TMD的基础上加上磁场能达到更好的减振效果，如磁耦合减振器在梁的减振方面的研究有：文献［7］分析了当机械部分达到很好的减振效果时的耦合参数的取值范围，以及非线性时的分岔和混沌与耦合参数的关系；文献［8］研究了多个有磁耦合的减振器串联时的稳定边界条件和分岔情况以及对应Lyaponov指数；文献［9］研究了磁TMD对梁的减振效果，结果显示在参数没有取最优的条件下，减振效果也比TMD的减振效果好。就目前情况来看，磁耦合减振器在高耸结构减振方面的研究还较为少见。本文在调谐质量阻尼器的基础上，将黏性阻尼器换成电磁阻尼器，建立了磁耦合调谐质量阻尼器（MC-TMD），系统地对MC-TMD系统的参数进行了优化研究，并进一步比较了TMD和MC-TMD的减振效果。

1 模型和运动方程

为了便于分析MC-TMD的动力学特性，考虑3个自由度的力学模型，如图1所示。该模型是在调谐质量阻尼器的基础上去掉黏性阻尼器，加上了电磁学部分形成电磁阻尼器，并通过力磁耦合把电磁学部分和原有的机械部分形成一个整体。调谐质量阻尼器是由质量m1与受外激励的振荡器相连，质量m2放在质量m1上，质量m2通过一个刚度系数为k2的弹簧与质量m1相连；电磁学部分是由电阻R、电感L和电容C组成的永久性磁铁。电磁学部分的作用是：当主体结构在遭受到外激励作用时，主体结构和TMD之间发生相对运动，带动线圈在磁场中运动，引起线圈磁通量的变化，产生感应电动势，作为电路的电源，同时通电线圈的运动会产生安培力，作为运动线圈的阻力来阻碍两者之间的相对运动，从而达到减振的效果。

图1 有磁耦合的TMD结构模型

根据牛顿定律和基尔霍夫定律，考虑安培力和感应电压的贡献，系统的微分方程如下：

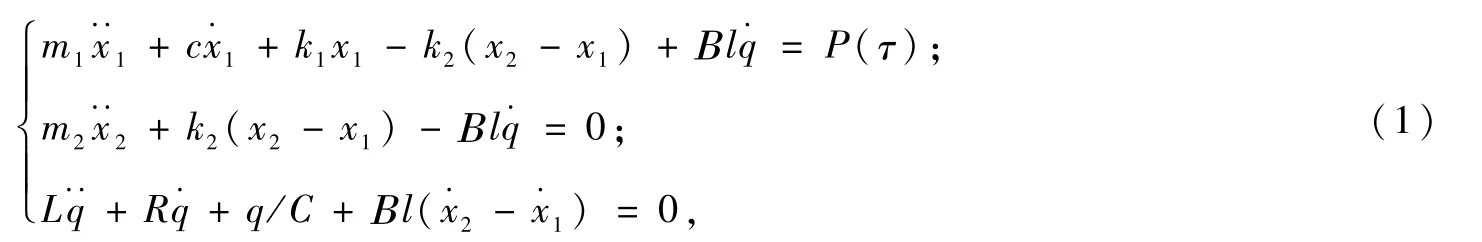
式中，m1和m2分别为主结构和TMD的质量；x1和x2分别为主结构和TMD的位移；“·”表示对时间求导；c为主体结构的阻尼系数；k1和k2分别为主结构和TMD的刚度；B为线圈所在处的磁场强度；l为在磁场B→m中线圈的有效长度；P（τ）为系统受到的简谐激励力；q为电容器极板上的瞬时电量；L、R和C分别为电感、电阻和电容。

为了便于参数优化的研究，下面对式（1）进行无量纲化处理，设无量纲变量为：

式中，Q0为电容器的参考电荷电量。

将上面的无量纲变量代入式（1），则方程（1）可化简为：

式（2）中，y1和y2表示主体的位移和TMD的位移；y3表示电容器的瞬时电量；ζ和γ分别为主结构阻尼比和电阻尼比；λ为电磁阻尼比；α为电力耦合系数；f1、f2和ω分别为TMD、振荡电路和简谐激励力的固有频率与主体结构的固有频率的比值；F0为简谐激励力的无量纲幅值；t为无量纲时间。

简谐激励力F0cos（ωt）傅里叶函数存在，并且初始条件为零，对方程（2）两边进行傅里叶变换可得

式中，Y1（ω），Y（ω），Y3（ω），F（ω）分别表示系统响应y1（t），y2（t）－y1（t），y3（t）和外激励f（t）的傅里叶变换。由方程（3）得到外激励和系统响应之间的傅里叶变换关系，

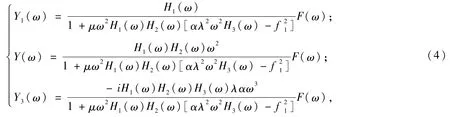
则系统主体结构的傅里叶函数为：

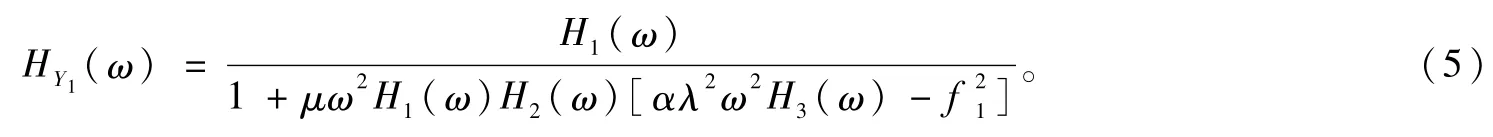
2 最优频率比的求解

2.1 理论求解

为了便于最优频率比的获取，将主体结构的傅里叶函数表示如下：

在对附着在无阻尼结构上TMD的最优设计研究中发现，存在两个固定点的频率，使主系统的振幅与TMD的阻尼无关［10］。本文模型是有阻尼的主体结构，在这里假定该模型也存在两个固定点频率，在此频率下，主体结构的振幅与TMD的电磁阻尼无关，即无论如何改变其他参数，这两个固定点频率所对应主体结构的幅值保持不变。根据这一假设，将存在λ＝0和λ＝∞时所对应的傅里叶函数模相等，即

由于μ≠0，ω≠0，所以式（7）就变成了关于ω2的一元二次方程，则有

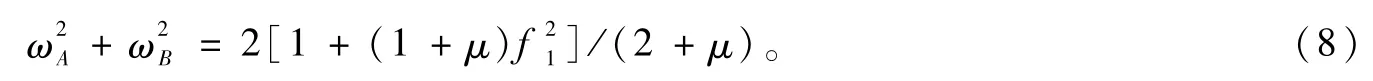
方程（9）化简后得

由式（8）和式（11）可得最优频率比为：

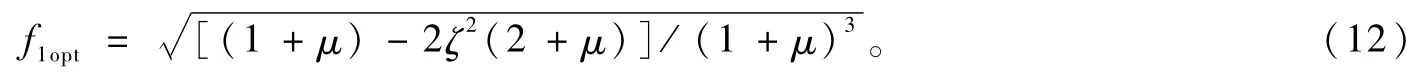
这样就得到了附着在阻尼结构上CD-TMD的最优频率比。如果是单自由度无阻尼结构（即ζ＝0），结果将与文献［11］的TMD系统最优频率比表达式［1／（1＋μ）］相一致。由式（12）可以看出：最优频率比只与主体结构的阻尼比和质量比有关，与其他的物理参数均无关。由式（12）得到的最佳频率比，在后面的参数优化讨论中，结合固定点的纵坐标为峰值，获得最优耦合参数及电系统阻尼比，使主体结构位移的傅里叶函数的幅值达到最小值，从而使主体结构在遭受更宽能量范围的外激励的响应减小，或者能使更宽范围固有频率的主体结构响应得到抑制。

2.2 数值验证

为了验证附着MC-TMD的阻尼轻质结构存在两个‘固定点’的可行性，本文利用数值计算方法对其进行了模拟。考虑质量比μ＝0.01和μ＝0.02，主体结构阻尼比为ζ＝0.01和ζ＝0.02。由于ζ≪1，4ζ2可以忽略不计，这样最优频率比就简化为［1／（1＋μ）］。对μ＝0.01，可以求得对应的频率比为0.99，并将频率比［1／（1＋μ）］代入方程（7），求出此条件下对应的两个固定点的理论值为1.029 4和0.959 2（考虑到固定点的频率为正）；同理，对于μ＝0.02，可以得到两个固定点的理论值为1.038 1和0.939 5（考虑到固定点的频率为正）。

利用数值计算方法可以获得主体结构响应的傅里叶函数随外激励频率比的变化曲线，如图2所示。当阻尼比ζ＝0.01时，不同的耦合参数λ的相交点和固定点非常接近，见图2a和图2b；当阻尼比ζ＝0.02时，不同的耦合参数λ的相交点和固定点比较接近，见图2c和图2d。从图2中可以看出：主体结构的阻尼比越小，固定点越趋近于一点，反之，固定点就越分散。在实际工程中，目前都向着高强轻质的方向发展，主体结构的阻尼比越来越小，因此‘固定点’法是可行的。

图2 CD-TMD系统主体结构位移的傅里叶函数

3 数值方法进行参数优化

参数的选取原则是：调控不同的耦合参数λ，使主体结构位移的傅里叶函数变化曲线的交点A和B在同一水平线上，设法降低这两点的傅里叶函数模高度，并使其成为曲线上的最高点。这样就可以使主体结构的傅里叶函数模的峰值被限制在A点和B点所对应的傅里叶函数模之下。由于在主结构的傅里叶函数表达式中参数α和λ总是以αλ2的形式出现，为了参数优化的方便，这里将αλ2看成一个参数，并设为β，这样傅里叶函数的表达式中的参数就可减少为：主结构和TMD的质量比μ，TMD和主体结构的固有频率比f1，LC振荡电路和主体结构的固有频率比f2，耦合参数γ、β。参数f2、γ和β最优值的选取原则，使傅里叶函数的表达式分别对f2、γ和β求导，并使导数在处为零，即，求出相应的参数f2、γ和β值，这些值就是它们最优值。但由于傅里叶函数的表达式比较复杂，TMD最优参数的解析式较复杂，很难求解。这里，把主体结构响应的傅里叶函数模的峰值最小作为优化目标，利用Matlab进行数值计算，寻求参数f2、γ和β的最优值，如图3所示。这里采用组合筛选法寻找参数f2、γ和β最优值，即将f2、γ和β的取值进行一一组合，求出每一组所对应的主体结构响应的傅里叶函数模的峰值，那么所有峰值中的最小值所对应的f2、γ和β，即为和βopt。这里，f2、γ和β的步长分别为0.000 1、0.005 0和0.001 0，精度可分别达到0.01%、0.50%和0.10%。在实际工程中要想达到更高的精度，则只需改变步长就可以了。

为了便于在设计中直接选用MC-TMD的最优参数，将不同质量比μ和不同主体结构阻尼比ζ所对应的最优TMD参数γopt和βopt，以及振动傅里叶函数模峰值的最小值列于表1中。在表1中还给出了f2＝1时的最优参数γopt和βopt以及此时的。比较两者可以看出：在相同的质量比和阻尼比条件下，两种情况的的值相差非常小。因此，在工程计算中为了方便起见，f2的值可以直接取1。由表1中的数据可看出：当质量比一定时，随着主结构阻尼比的增加参数f2、γ和β的最优值的变化非常小，但是减振效果变化却非常大。但对于阻尼比一定而质量不同时，振荡回路最优阻尼比γopt、最优参数βopt变化就相对较大一些。由此看来，质量比对优化参数的影响大于阻尼比的影响。

图3 参数优化步骤

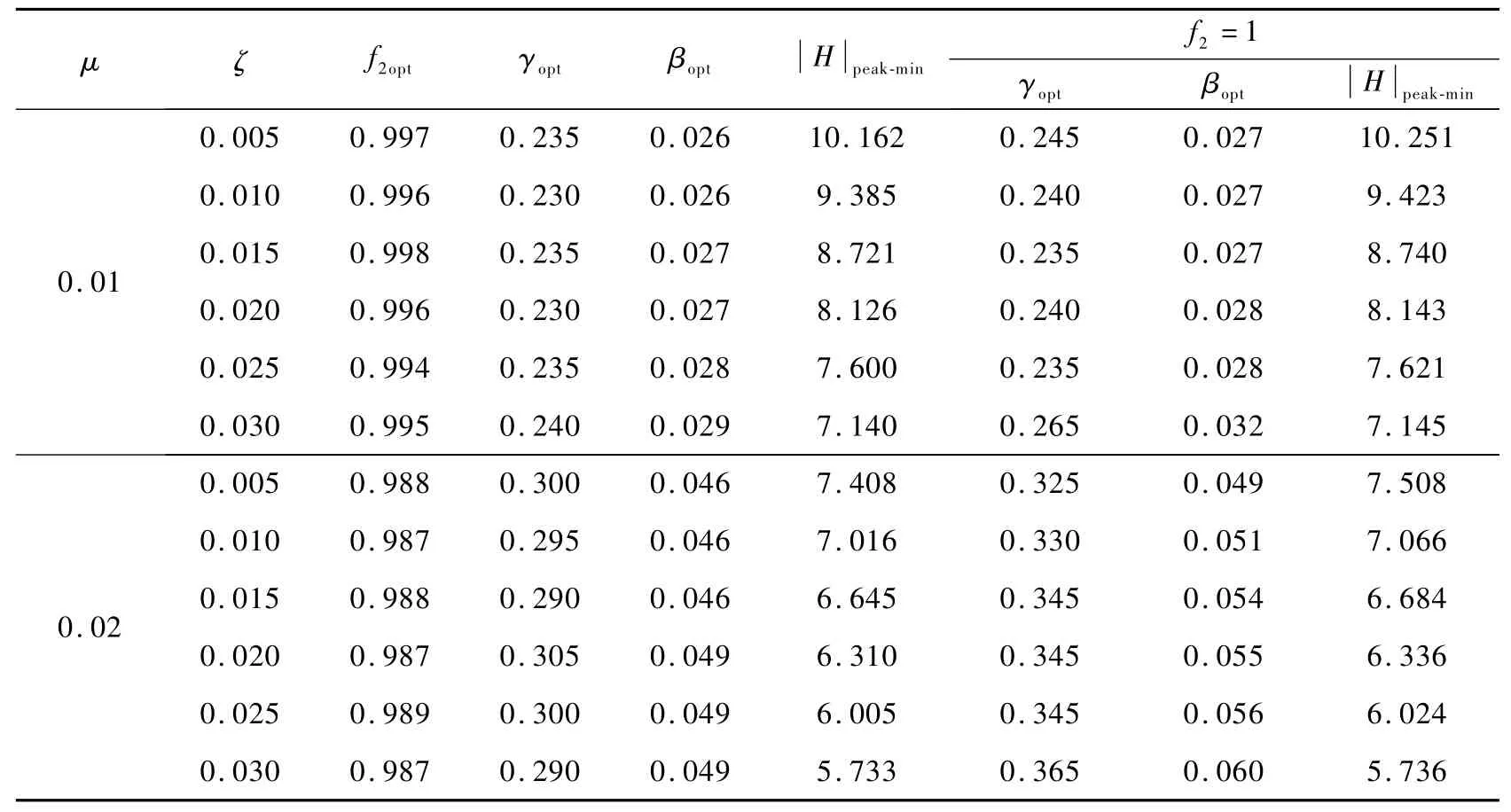
表1 MC-TMD系统最优参数设计

4 减振效果的比较

下面通过讨论MC-TMD和普通TMD在主体结构阻尼比和质量比相同条件下的减振情况，对它们的减振效果进行比较。这里取ζ＝0.01、μ＝0.01和ζ＝0.02、μ＝0.01，对于普通TMD采用文献［12］中的最佳频率比和阻尼比的设计：

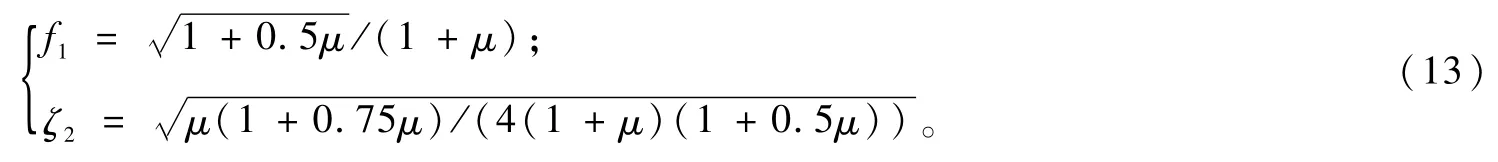
而对MC-TMD，采用本文所获取的优化参数。通过主体结构的响应随外激励频率比变化的曲线来比较两者的减振效果，如图4所示。从图4中可以看出：当主体结构的固有频率和外激励力的频率达到共振时，两者的减振效果有较大的差别，MC-TMD的优势就突显出来了。很明显，无论是大阻尼还是小阻尼，MC-TMD在较宽的频率范围，其主体结构傅里叶函数的模趋于稳定，并且MC-TMD比普通TMD的减振效果也有显著的提高，其减振效果提高了20%左右。

5 结论

（1）主结构的最优阻尼比只与主体结构的阻尼比和质量比有关，与其他的物理参数均无关，并且当阻尼比为零时，与文献［11］的TMD系统最优频率比表达式［1／（1＋μ）］相一致。

（2）质量比对振荡回路最优阻尼比γopt、最优参数βopt的值影响较大，而主结构阻尼比对上述参数的影响几乎可以忽略不计；LC振荡电路和主体结构的固有频率比f2取1和取最优值减振效果几乎一样，因此在工程计算中可以直接取1。

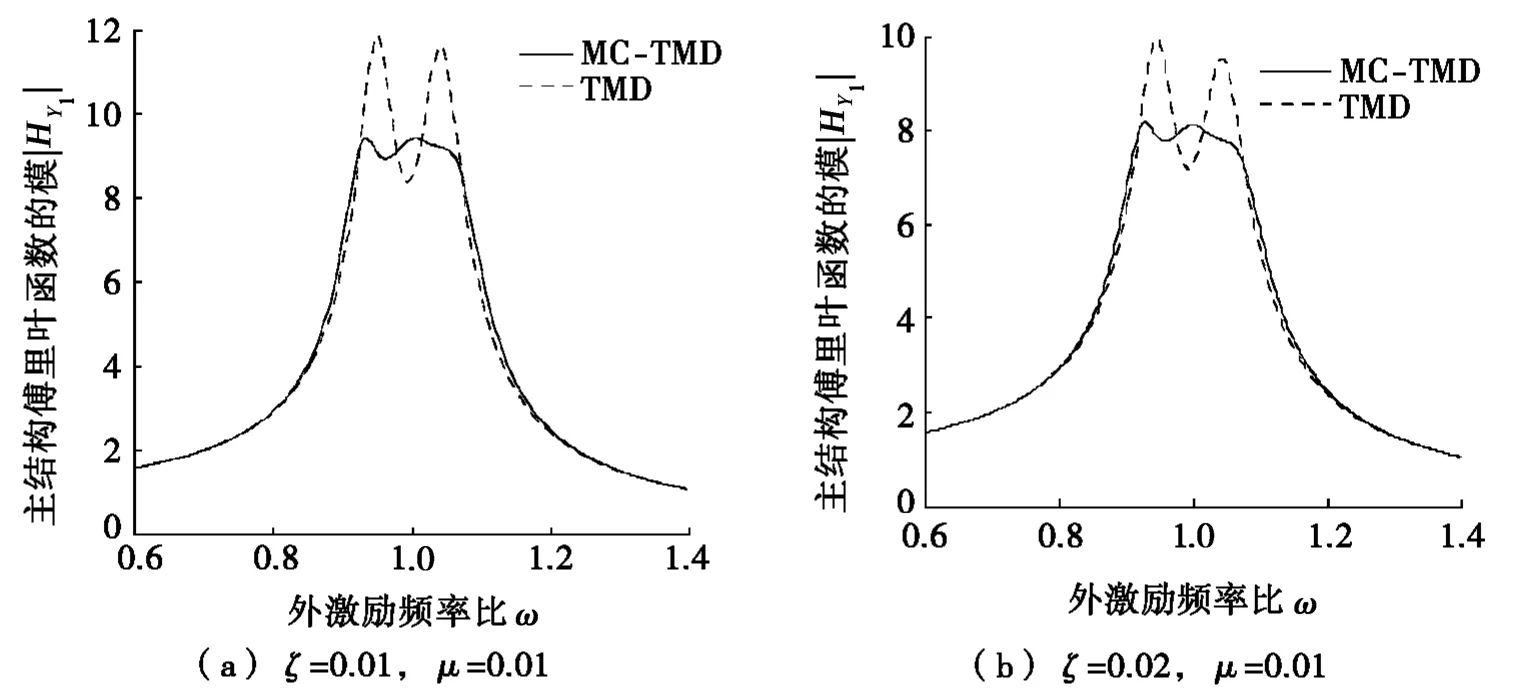
图4 外激励频率比对减振效果的影响

（3）在相同主体结构和相同TMD下，频率比在1附近（即共振）时，无论是大阻尼还是小阻尼，MCTMD比TMD的减振效果有显著的提高，其减振效果提高了20%左右。

在风振多发的地区还可以将电阻转换成电炉丝将风能转换成热能，制成风能热水器。这样既能减振又能转害为宝。

［1］Benedikt W，Glauco F.Assessment of Long-term Behavior of Tuned Mass Dampers by System Identification［J］. Engineering Structures，2010，32（11）：3670－3682.

［2］ Moutinho C.An Alternative Methodology for Designing Tuned Mass Dampers to Reduce Seismic Vibrations in Building Structures［J］.Earthquake Engineering＆Structural Dynamics，2012，41（14）：2059－2073.

［3］ Lu X L，Ding K，Shi W X.Tuned Mass Dampers for Human-Induced Vibration Control of the Expo Culture Centre at the World Expo 2010 in Shanghai，China［J］.Structural Engineering and Mechanics，2012，43（5）：607－621.

［4］ 李晓华，王宝基，闫安志.双边塑性碰撞调谐质量阻尼器的位置控制［J］.河南科技大学学报：自然科学版，2012，33（2）：92－96.

［5］ 李晓华，闫安志.基于塑性碰撞的调谐质量阻尼器参数优化研究［J］.河南理工大学学报：自然科学版，2009，28（3）：340－346.

［6］ Rakicevic Z T，Bogdanovic A，Jurukovski D.Effectiveness of Tune Mass Damper in the Reduction of the Seismic Response of the Structure［J］.Bulletin of Earthquake Engineering，2012，10（3）：1049－1073.

［7］ Yamapi R.Dynamics of an Electromechnical Damping Device with Maganetic Coupling［J］.Communications in Nonlinear Science and Numerical Simulation，2006，11（8）：907－921.

［8］ Woafo P，Yamapi R，Chabi O J B.Dynamics of a Nonlinear Electromechnical System with Multiple Function in Series［J］. Communications in Nonlinear Science and Numerical Simulation，2005，10（3）：229－251.

［9］ Bae J S，Hwang J H，Roh J H，et al.Vibration Suppression of a Cantilever Beam Using Magnetically Tuned-Mass-Damper［J］.Journal Sound of Vibration，2012，331（26）：5669－5684.

［10］ Mallik A K.Principles of Vibration Control［M］.New Delhi：Affiliated East West Press Pvt Ltd，1990.

［11］ Den H J P.Mechanical Vibrations［M］.4 ed.New York：McGraw Hill，1956.

［12］ Warburton G B.Optimum Absorber Parameters for Various Combinations of Response and Excitation Parameters［J］. Earthquake Engineering and Structural Dynamics，1982，10（3）：381－401.

TU473

A

1672－6871（2014）04－0086－06

国家自然科学基金项目（11003003）；河南省基础与前沿技术研究计划基金项目（112300410277）；河南省科技厅重点攻关项目（122102310279）；河南省高校青年骨干教师基金项目

李晓华（1976－），女，河南许昌人，实验师，硕士，研究方向为振动、冲击和减振.

2013－11－01