圆度误差的二分法逼近搜索评定

李 飞，雷贤卿，崔静伟，王海洋

（河南科技大学机电工程学院，河南 洛阳 471003）

圆度误差的二分法逼近搜索评定

李 飞，雷贤卿，崔静伟，王海洋

（河南科技大学机电工程学院，河南 洛阳 471003）

结合圆度误差的定义及其几何特征，提出了一种新的圆度误差评定算法——圆度误差的二分法逼近搜索评定。首先，将被测圆轮廓上测量点的直角坐标数据转化为极坐标数据，分别以极角和极径为横、纵坐标轴建立新的坐标系，实现被测点的线性化处理，将圆度误差的求解问题转化为直线度误差的求解问题。然后，用二分法逼近搜索的方法，对转化后的直线度误差进行最小区域评定，从而实现了圆度误差的最小区域评定。阐述了圆度误差线性化处理的方法和二分法逼近搜索的原理及实现过程。实例验证结果表明：该算法可以有效、正确地评定圆度误差。

误差评定；圆度误差；线性化；直线度误差；二分法逼近搜索

0 引言

圆度误差是机械零件最基本的几何要素之一，它反映的是实际圆相对于理想圆的变动量。圆度误差值的大小是以包容实际轮廓的两个同心圆的半径差来衡量的。其评定方法的核心是根据被测圆轮廓上的点找出理想的评定圆心。是否能准确有效地评定圆度误差，直接影响到机械产品的性能和寿命。国标规定的评定方法有最小二乘法、最小区域法、最大内接圆法和最小外接圆法。其中，最小二乘法是最常用的评定方法，其算法计算简便且有唯一解，但其评定原理不符合形状误差评定的最小条件准则［1］。最小区域法是符合国标准则的误差评定方法，但实现最小区域的过程是解决多极值的非线性最优化问题，因此不易直接求解。国内外学者利用多种数学方法对圆度误差的最小区域评定算法进行了研究，比较有代表性的算法有：仿增量算法［2］、刚体坐标变换算法［3］、搜索算法［1，4－5］、遗传算法［6－7］、计算几何算法［8］、最陡下降算法［9］及线性化算法［10］等；这些成果都有一定的实用价值，但这些算法大都比较复杂，不易被实际应用。

本文结合圆度误差的定义、几何特点，提出了一种新的圆度误差评定算法—圆度误差的二分法逼近搜索评定，实现圆度误差的快速准确评定。

1 圆度误差数据的线性化过程

由于直线度误差的评定比圆度误差的评定相对容易，因此，通过直角坐标与极坐标的转换，先将被测圆轮廓线性化处理，使圆度误差的评定问题转化为直线度误差的评定［10］。

设在直角坐标系XOY中，被测圆轮廓上的测量点为Pi（xi，yi）（i＝1，2， ，N，N≥4）。在提取点中选取大致均匀分布的3个测量点，由此3点拟合圆心坐标O′（x0′，y0′），或者按式（1）确定圆心坐标O′（x0′，y0′），以O′（x0′，y0′）为坐标原点建立新的直角坐标系X′O′Y′（见图1）。

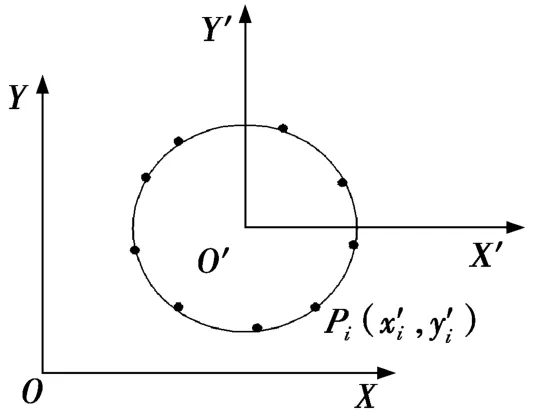
图1 新建直角坐标系X′O′Y′

在新的直角坐标系X′O′Y′中，测量点Pi（x′i，y′i）的值由式（2）给出：

以新直角坐标系的O′X′轴作为极坐标变换的起始直线，逆时针方向取测量点的极角，将直角坐标系X′O′Y′中的测量点坐标转化为极坐标形式（见图2）。则各测量点Pi（θi，ρi）的极坐标由式（3）计算出：

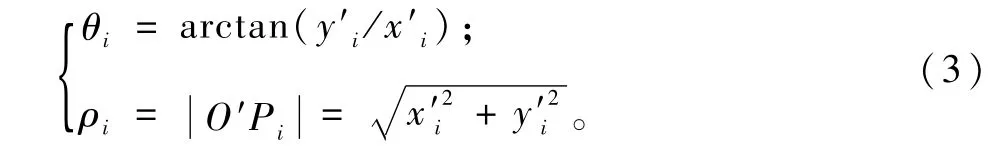
以极角θ为横坐标，以极径 ρ为纵坐标，建立新的直角坐标系θiO″ρi（见图3），即沿圆心O′将被测圆周展开成一条直线，则被测圆轮廓上的测量点就转化为“直线”上的测量点。（为了尽量的减小误差，必须保证圆心O′与原点O″在同一位置。）这样就把圆度误差的评定问题转化为直线度误差的评定问题，转化后“直线”的直线度误差就是被测实际圆的圆度误差。

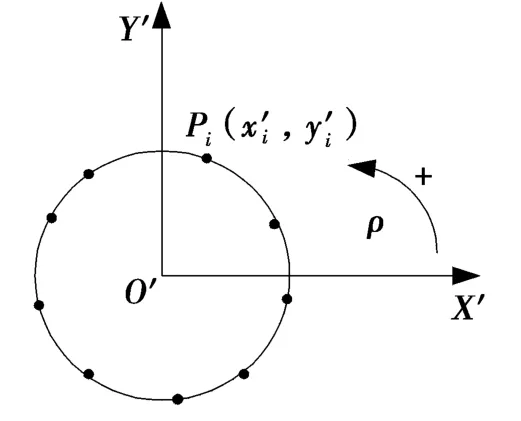
图2 直角坐标转化为极坐标

2 二分法逼近搜索评定过程

直线度误差的二分法逼近搜索评定算法的原理是：首先，确定假设的直线两端点坐标，以直线的两个端点为参考点，在与纵坐标平行的方向上按一定长度值（如估计的直线度误差值）分别布置区域并构造辅助点，连接所构造的辅助点可得到4条线段，即假设的理想中心线。计算测量点到这4条线段的距离，可得4个距离的极差值（测量点与每条线段的距离的最大值和最小值之差），其中，最小者用F1表示。同样地，计算测量点到初始直线距离的极差值，用△D表示。然后比较F1与△D的大小。如果F1＜△D，那么起始参考点就变为与F1相对应的假设理想中心线的端点，构造新的辅助点；如果F1≥△D，则参考点不变，将误差区域缩小一倍，构造新的辅助点。如此不断重复，直到满足直线度误差评定要求。

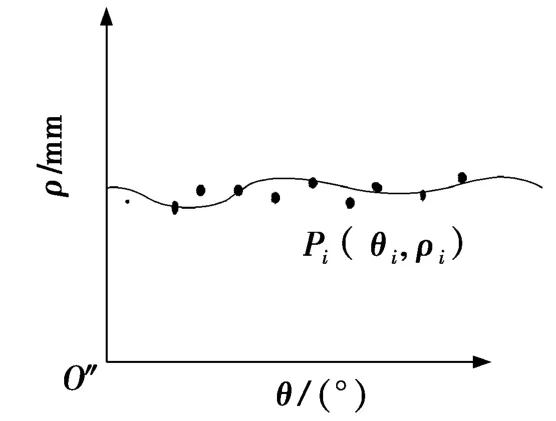
图3 线性化后的“直线”

2.1 构造最小区域的假设理想中心线

设转化后“直线”的两端点分别为P1（θ1，ρ1）和PN（θN，ρN）。

首先，将端点 P1设为参考点（如图4所示），创建两个辅助点 P11（θ11，ρ11）和 P12（θ12，ρ12），且（为了使理想中心线包容在其范围内，e的值至少为直线度误差值的两倍）。此时，两个辅助点P11（θ11，ρ11）、P12（θ12，ρ12）的坐标由式（4）给出。

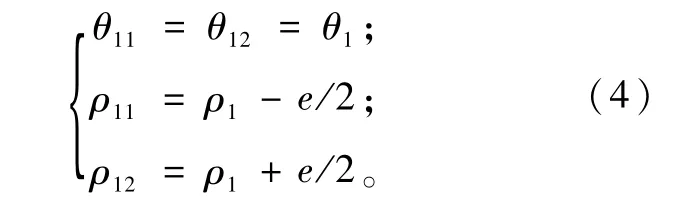
同样地，设端点PN（θN，ρN）为参考点（如图4所示），创建两个的辅助点PN1（θN1，ρN1）和此时，两个辅助点PN1（θN1，ρN1）、PN2（θN2，ρN2）的坐标由式（5）给出。

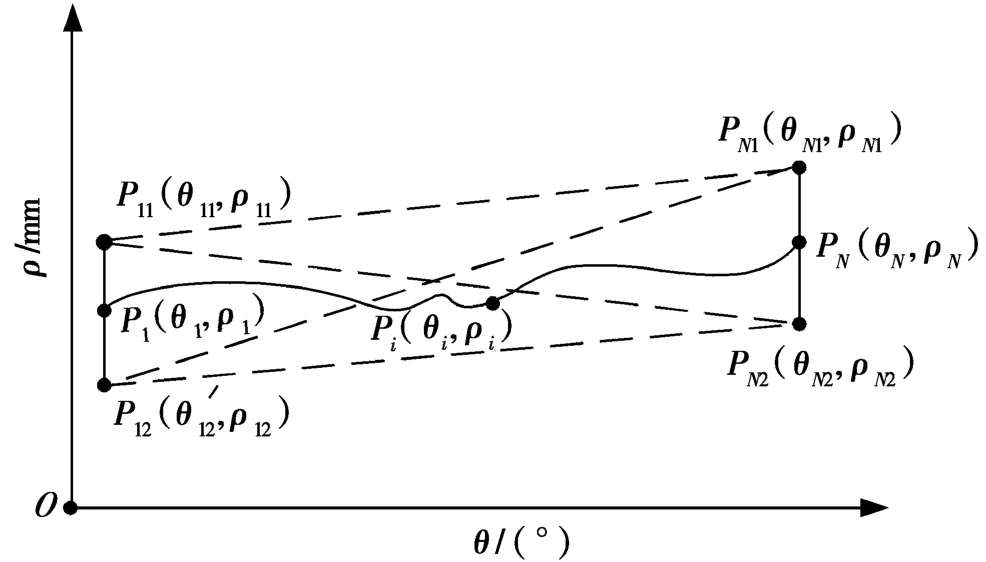
图4 二分法逼近搜索的算法原理图

将上述创建的4个辅助点两两相连，可得到4条假设理想中心线（P11PN1，P11PN2，P12PN1和P12PN2）。若设假设理想中心线的方程为y＝kx＋b，其斜率k和截距b的表达式为：

同样地，“直线”的最初两端点P1（θ1，ρ1）和PN（θN，ρN）之间的线段也可看作是假设的理想中心线，其斜率K和截距B的表达式为：

2.2 计算所有测量点与4条假设理想中心线之间距离的极差值

利用式（8）计算所有测量点Pi（θi，ρi）与4条假设理想中心线之间的距离，并计算出所有测量点与每一条假设理想中心线之间距离的极差值（距离的最大值与最小值之差）。由于有4条假设的理想中心线，那么就可以得到4个距离的极差值。由平面直线度的定义可知：4个极差值中的最小者就是直线度误差，用F1来表示。

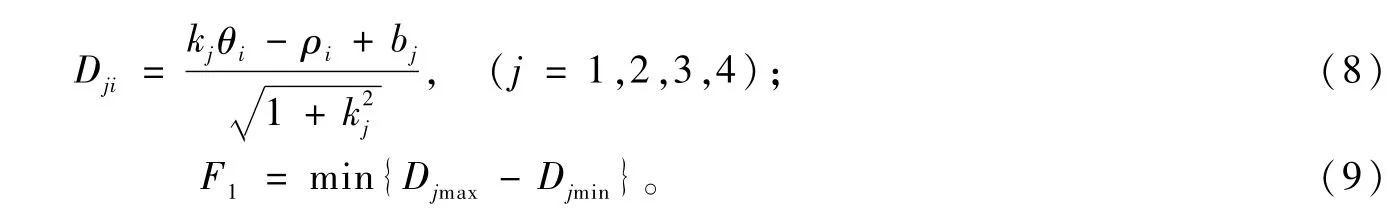
2.3 计算所有测量点与两个参考点所构成的直线之间距离的极差值

根据式（10）算出所有测量点Pi（θi，ρi）与P1PN的距离，其距离的极差值用△D表示（△D＝Dmax－Dmin）。

2.4 二分法逼近搜索方法

比较F1和△D。如果F1＜△D，说明极差F1所对应的假定理想中心线更接近于理想中心线，那么起始参考点就变为与F1相对应的中心线的端点，例如，与F1相对应的假设理想中心线为P11PN2，则参考点就变为该线段的两个端点P11（θ11，ρ11）和PN2（θN2，ρN2），创建新的辅助点，重复2.1～2.4。如果F1≥△D，说明极差△D所对应的中心线更接近于理想中心线，那么参考点不变，将误差区域缩小1倍（亦即e＝0.5e），构造新的辅助点，重复2.1～2.4。

当e的值小于定值δ（一般地，δ＝0.000 1 mm），可以认为搜索到的假定理想中心线已经非常接近理想中心线，停止搜索。此时，F1和△D中的较小者就是平面直线度误差，较小者用F表示，则

由上述步骤可知：得到的F是包含所有测量点Pi（θi，ρi）的两条平行直线之间的距离，逆向操作，此平行直线则转变为半径不同的两个同心圆（半径差为F），由圆度误差的定义可知：F即为圆度误差值。

2.5 求取圆心坐标

结合2.4，在与F对应的中心线上均匀的提取3个点M1（θl，ρl）、M2（θm，ρm）和M3（θn，ρn），该中心线可看作是一个圆的展开线，那么提取的3个点就是某个圆上均布的3个点。利用式（12）将其坐标值转化为直角坐标。

设该圆的圆心和半径分别为O0（a，b）和R，依据3点确定一个圆的原理，圆心O0（a，b）的坐标由式（13）得出：

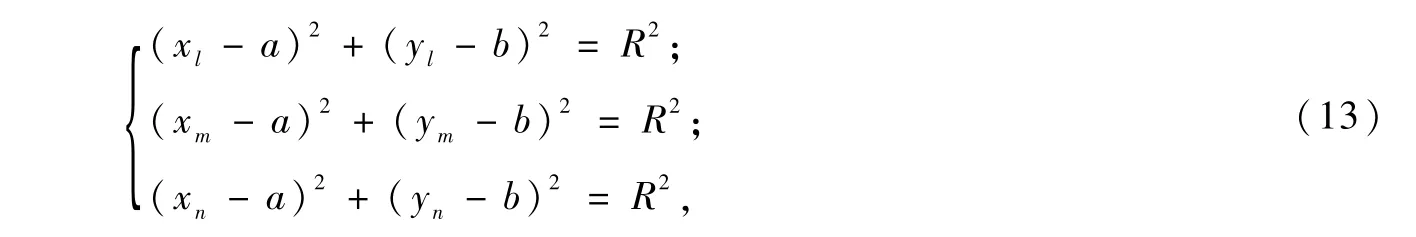
其中，

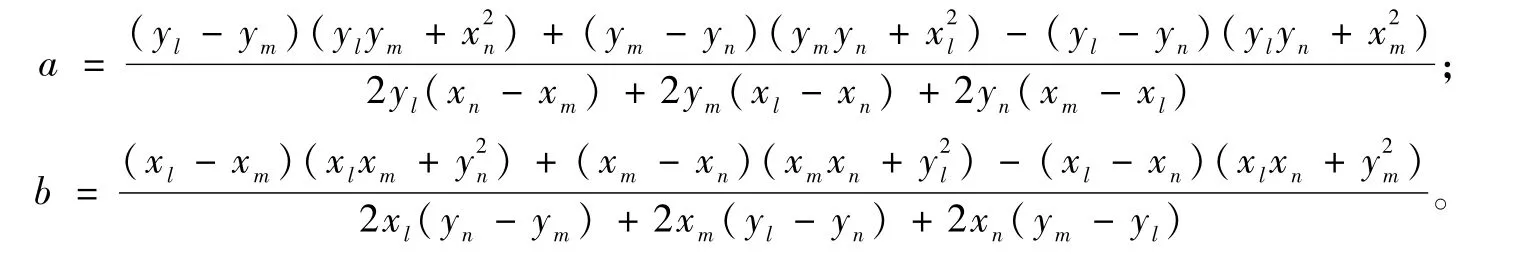
式（13）得到的a、b的值在直角坐标系X′O′Y′下的圆心坐标，依据坐标平移原理，则在直角坐标系XOY内的圆心O0（X0，Y0）坐标为：

3 实例验证

文献［1］和文献［10］对同一组数据采用不同的评定算法得出了与三坐标测量机相一致的结果，验证了所提评定算法的正确性。本文实例采用文献［1］的数据，初始参考点选取坐标变换后第一个测量点和最后一个测量点，终止搜索条件为 δ＝0.000 1 mm，所得结果见表1。

由表1可以看出：本文所提算法计算得到的圆度误差与文献［1］和文献［10］中求得的圆度误差相一致，根据微误差取舍准则，结果是可以信赖的，说明该评定算法可以实现圆度误差的评定。

表1 数据处理结果

4 结论

本文介绍了圆度误差的二分法逼近搜索评定算法的原理及运用该算法实现圆度误差评定的过程。本文提出的算法，原理简单，直观，便于编程，具有通用性和较好的实用性，对测样点的分布没有要求。实例验证了算法的正确性，为圆度误差的有效评定提供了一套新的评定算法。

［1］ 黄富贵，郑育军.基于区域搜索的圆度误差评定方法［J］.计量学报，2008，29（2）：117－119.

［2］ 岳武陵，吴勇.基于仿增量算法的圆度误差快速准确评定［J］.机械工程学报，2008，44（1）：87－91.

［3］ Endrias D H，Feng H Y.M inimum-zone form Tolerance Evaluation Using Rigid-body Coordinate Transformation［J］. Journal of Computing and Information Science in Engineering，2003，3（1）：31－38.

［4］ 雷贤卿，畅为航，李济顺，等.圆度误差的网格搜索算法［J］.仪器仪表学报，2008，29（11）：2324－2329.

［5］ 涂鲜萍，李飞，雷贤卿，等.平面度误差的遍历搜索算法［J］.河南科技大学学报：自然科学版，2013，34（5）：19－22.

［6］ 崔长彩，车仁生，叶东.基于遗传算法的圆度误差评估［J］.光学精密工程，2001，9（6）：499－503.

［7］ 温秀兰，张鹏.进化策略实现圆度误差的统一评定研究［J］.计量学报，2008，29（2）：106－109.

［8］ Samuel G L，Shunmugam M S.Evaluation of Circularity from Coordinate and form Data Using Computational Geometric Techniques［J］.Precision Engineering，2000，24（3）：251－263.

［9］ Zhu L M，Ding H，Xiong Y.A Steepest Descent Algorithm for Circularity Evaluation［J］.Computer-Aided Design，2003，35（3）：255－265.

［10］ 黄富贵，董兆鹏.圆度误差评定的线性化处理方法［J］.华侨大学学报，2011，32（5）：492－494.

TH164；TH161

A

1672－6871（2014）02－0020－04

国家自然科学基金项目（50875076）；河南省基础与前沿技术研究计划基金项目（122300410114）

李 飞（1987－），男，河南洛阳人，硕士生；雷贤卿（1963－），男，河南洛宁人，教授，博士，硕士生导师，主要从事精密测试技术研究.

2012－10－09