浅水域爆炸冲击波传播特性

何 理，钟冬望，司剑锋

(武汉科技大学a.资源与环境工程学院;b.爆破技术研究中心，湖北武汉430081)

0 引言

在针对水下爆破工程、水中兵器破坏效应研究中，爆炸冲击波在水中的传播特性研究一直是问题的关键。其传播影响因素众多，较为复杂，国内外很多学者作了这方面的研究，大多以试验研究为主。近年来，随着计算机技术与有限元方法的快速发展，人们通过数值模拟可以较准确地描述水下爆炸的各种现象。目前，国内外多采用ANSYS/LS-DYNA、AUTODYN等有限元数值模拟软件，寻求水下爆炸冲击波的传播特性和传播衰减规律。

文献［1］通过数值模拟计算得到水下钻孔爆破时，在与炮孔轴线成一定角度范围内，地震动水压力与冲击波叠加使得冲击波峰值压力随爆距增加单调减小，但并未通过实验数据的验证;文献［2］结合工程实践，主要通过试验手段测得水下钻孔爆破爆炸冲击波峰值压力数据及冲击波波形，通过线性拟合，得到冲击波峰值压力随时间、距离、高程的衰减规律;文献［3］主要通过试验手段针对水深因素对近岸海底浅水钻孔爆破水中冲击波压力峰值的影响进行了初探，取得了部分成果。但同时结合试验分析与数值计算对浅水域爆炸冲击波传播特性方面的研究相对较少。

本文采用美国PCB公司ICP水下冲击波测量长型传感器，对浅水域中爆炸冲击波进行数据采集试验，对冲击波波形及峰值压力进行分析研究，结合数值模拟，得到浅水域爆炸冲击波传播特性相关规律。为进一步研究深水下爆炸冲击波传播特性以及水下结构物在爆炸荷载作用下的动态响应积累了经验。

1 试验研究

1.1 试验测试系统

试验所采用的传感器为美国ICP水下冲击波测量长型传感器，此系列传感器使用对容积变化敏感的电气石晶体，内置集成电路放大器。具有无谐振、高电压输出、可驱动长电缆等特点。所能承受静压范围为:Pmax≤345 MPa。测试系统主要由压力传感器、信号变换及放大电路、记录器等组成。数据采集处理系统为成都佳仪科技发展有限公司的PCI4712数据采集和分析系列产品。配套分析软件具有实时测量、回放分析、数据转换等功能。为保证足够的安全距离，试验中通过特殊延长线连接传感器与记录仪。传感器各通道灵敏度因数分别选取29.82、14.51、743.80。

本次试验拟采用8号瞬发电雷管(每发TNT当量1.07 g)［4］模拟水下炸药爆炸，起爆点设在水深1.5 m处，传感器依次置于距爆源0.5 m、1.0 m、2.4 m处，分一发起爆、两发同时起爆两组试验。采集分析仪采样频率设为5 MHz，采样长度取1 000K(K=10 个样点数)，负延时，量程取0.2 V，触发电平为0.03 V。由于爆源几何尺寸与各测点爆距相比非常小，不在同一数量级，且TNT当量很小，故将试验视作球形药包浅层水域爆炸。试验方案布置如图1所示。

图1 试验方案测点布置图(单位:m)

1.2 试验数据及分析

通过试验测得两发雷管起爆时距离爆源0.5 m处冲击波波形曲线，如图2所示。

由图2可以看出:炸药爆轰结束后形成冲击波，冲击波峰值压力上升迅速，且随时间衰减明显，自由水面使波峰尾部被截断。波峰后面基本类似于“白噪声”特性，脉动持续时间比较长，具有强度不大的变向压力。爆炸产物形成的“气泡”在水中不断膨胀，收缩，进行振荡并不断上浮，产生气泡脉动，通常，气泡首次脉动形成的压力波(即二次压力波)才有实际意义。

不同测点处冲击波压力时程曲线如图3所示。根据图3中水平测线各测点水击波波头到达的时间差及测点间距来分析，计算得到水击波浅水域中传播平均速度在1 700 m/s左右。

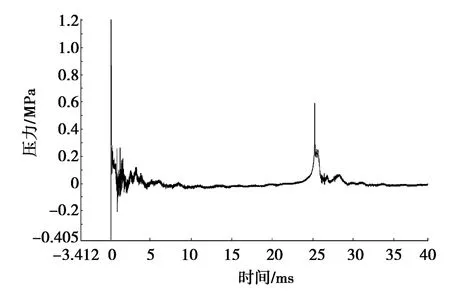
图2 冲击波与二次压力波波形图

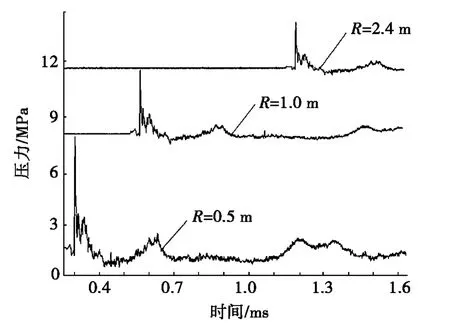
图3 不同测点处冲击波压力时程图

不同试验条件下测得冲击波峰值压力如表1所示。

表1 试验数据

由表1可以看出:随着测点与爆心距离的直线增加，冲击波峰值压力逐渐减小。同一爆心距下，峰值压力随药量的增加逐渐变大。

装药在水域中爆炸的峰值压力计算，大多采用Cole P的经典峰值压力公式形式:

式中，Pm为峰值压力，105Pa;Q为装药量;R为距爆心的距离;K、α是和炸药及环境条件相关的系数。通过对表1中数据进行拟合，得到静态水域爆炸冲击波峰值压力Pm=601.85(Q1/3/R)1.429，0.043＜(Q1/3/R)＜0.205。

试验中计算的K及α明显大于国内一些水下钻孔爆破实测所得的相关系数，分析其原因，主要是由于此次试验为浅水域裸露爆破，相对于水下钻孔爆破，水介质对冲击波的压力削弱不大，且测点位置距离水平面位置在0.5～3.0 m小范围内，水中冲击波压力衰减不是非常明显。

图4 冲击波压力衰减曲线

水中冲击波压力随时间变化的关系为［5］:式中，Pm为水中冲击波初始峰值，Pa;θ为衰减时间常数，即由Pm衰减到Pm/e所需的时间，s。提取冲击波典型压力时程进行水平轴放大并进行指数拟合得到图4，得出冲击波指数衰减规律为:

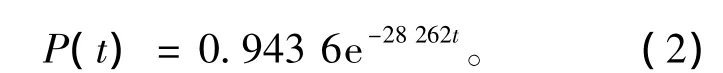
2 数值模拟

模拟采用LS-YDNA程序的ALE算法来实现。ALE算法可以克服单元严重畸变引起的数值计算困难，并实现流—固耦合的动态分析［6］。由于本次模拟具有对称性，取四分之一模型进行计算。模型大小为300 cm×150 cm。用球形药包爆炸模拟雷管起爆，炸药从球心起爆。建立模型采用cm-g-μs单位制，计算时间为1 500 μs。根据试验方案设计，取R1=0.54 cm、R2=0.73 cm，分别模拟水下一发雷管爆炸(1.07 g)和两发同时爆炸(2.14 g)时浅水域爆炸冲击波的传播，根据传感器位置依次选取模型中对应单元。计算模型尺寸如图5所示。

模型计算涉及炸药和水两种材料，材料的计算模型和参数如下:

(Ⅰ)炸药采用EOS-JWL状态方程［7］进行数值模拟，炸药参数如表2所示(表2中，ρ为炸药密度;D 为炸药爆速;A、B、R1、R2、ω 为描述 JWL方程的5个独立物理常数;E0为初始比内能)。

图5 模型尺寸(单位:cm)

表2 炸药参数

(Ⅱ)水的状态采用GRUNEISEN方程［8］，其形式如下:

式中，P为压力;C为剪切—压缩波速曲线截距;S1、S2、S3为剪切—压缩波速曲线斜率系数;γ0为GRUNEISEN常数;E为初始比内能;ρ、ρ0分别为材料密度、材料初始密度。

通过模拟计算，得到水下爆炸冲击波波形，如图6所示。

对比图2与图6可知:数值模拟水下冲击波压力峰值较实测值上升缓慢，由于有限元不可能反应这种强间断，所以冲击波到达水中某点时，压力的爬升需要一定的时间，爬升时间与网格密度有关。在峰值压力值过后，计算值与实测值均会有较大的扰动，出现压力的双峰或多峰现象，从这一点上来看，数值模拟的这种脉动符合实际情况。

数值模拟计算得到不同时刻水中应力场分布，如图7所示。

图6 数值模拟典型水中冲击波波形

图7 不同时刻水中应力场分布

从图7a可以看出:炸药爆轰刚刚结束，应力场强度较大，应力量级较高，但应力场范围较小，集中在起爆点附近区域，应力波还未来得及向四周传播。随着时间的增加，从图7b和图7c可以看到:应力波以圆形波阵面逐渐向外传播，随着应力场向四周传播，起爆点附近应力场强度出现衰减，应力场总体强度逐渐减小。764.980 μs时刻，应力波到达水面自由面，如图7c所示。随着应力波的继续传播，在自由面处发生反射、透射现象，导致自由面处爆炸波应力场急剧减弱，如图7d所示。

试验数据与数值模拟结果对比见表3。

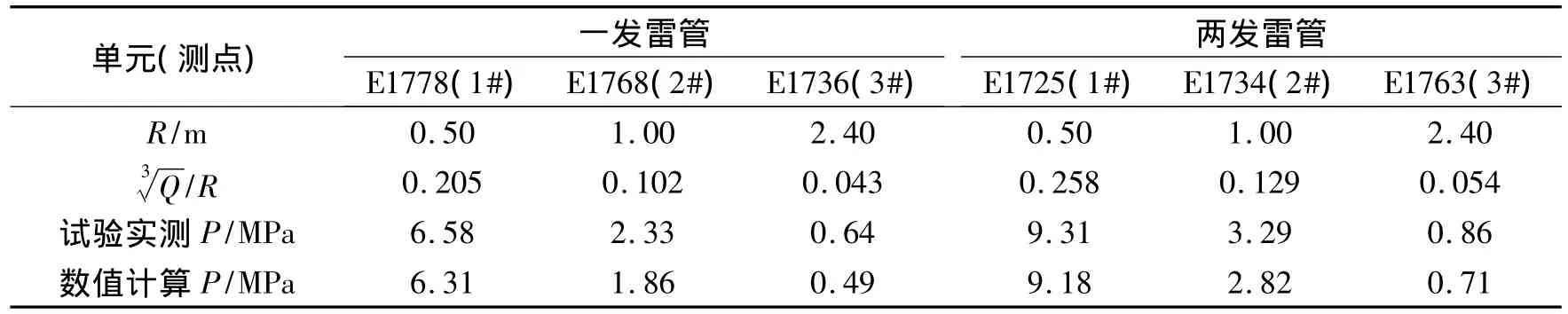
表3 试验数据及数值计算结果

从表3可以看出:数值模拟各测点冲击波峰值压力随爆距的增加逐渐减小，同一爆距处，炸药量越大，峰值压力也越大，与实际情况符合，验证了数值方法模拟水下爆炸冲击波传播特性的适应性。数值模拟各测点峰值压力与试验值均在同一量级，说明了本次模拟算法的正确性。表3中，数值计算的各测点峰值压力均较实测值小，主要是由于模拟中为节省计算时间，划分网格密度较小所造成［9-11］。水介质状态方程参数过低，也将影响冲击波峰值压力。

当两发雷管同时起爆时，在同一水平测线(水深1.5 m)依次选取爆心距为0.5 m、1.0 m、1.5 m处对应单元，单元编号分别为E1778、E1768、E1760，得到其压力随时间的变化曲线，如图8所示。

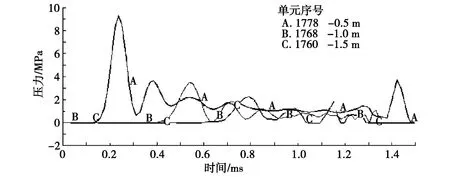
图8 单元压力时程曲线

从图8可以看出:离爆心距离近，质点峰值压力下降非常快，距离较远时，压力下降缓慢，爆炸近场区压力衰减速度明显快于远场区。从水平测线各测点爆炸波波头到达的时间差及测点间距来分析计算，计算得到爆炸波浅水域中传播平均速度在1 600 m/s左右，与水中纵波波速1 500 m/s相当［10］，与其他类似工程实测结果相符，进一步验证了数值方法研究爆炸冲击波传播特性的适应性。综合图3与图8，可以得到结论:试验情况下爆炸冲击波水平方向传播速度约为1 500～1 700 m/s。

3 结论

(1)通过对实测数据进行线性回归拟合分析，得到静态浅水域爆炸冲击波峰值压力:Pm=601.85×(Q1/3/R)1.429×105Pa，0.043＜(Q1/3/R)＜0.205;冲击波压力随时间衰减规律为:P(t)=0.943 6e-28262t×106Pa。

(2)数值方法模拟爆炸冲击波传播过程，炸药爆轰结束后，应力波以圆形波阵面向外传播，随着应力场向四周传播，起爆点附近应力场强度出现衰减，应力场总体强度逐渐减小。随着应力波的继续传播，在自由面处发生反射、透射现象，导致自由面处爆炸波应力场互相抵消，能量溢出，应力场强度急剧减弱。

(3)爆炸近场区峰值压力衰减速度较远场区快。

(4)试验情况下爆炸冲击波水平方向传播速度约为1 500～1 700 m/s。

［1］高明涛，李昕，周晶.水下钻孔爆破水中冲击波的数值模拟研究［J］.水电能源科学，2009，27(4):138-142.

［2］Si J F，Zhong D W，Li L N.Experimental Research on Shock Wave in Water of Underwater Drilling Blasting［J］.Applied Mechanics and Materials，2012，193/194:989-994.

［3］邵鲁中，龙源，孙远征，等.水深因素对水下钻孔爆破冲击波压力峰值的影响［J］.爆破器材，2008，37(3):4-6.

［4］钟帅，张立.深水下8号雷管爆炸冲击波参数的研究［J］.煤矿爆破，2007(1):4-6.

［5］孙远征，龙源，邵鲁中，等.水下钻孔爆破水中冲击波试验研究［J］.工程爆破，2007，13(4):15-19.

［6］殷有泉.非线性有限元基础［M］.北京:北京大学出版社，2007:322-331.

［7］吴亮，位敏，钟冬望，等.空气间隔装药爆破动态应力场特性研究［J］.爆破，2009，26(4):17-21.

［8］时党勇，李裕春，张胜明.基于ANSYS/LS-DYNA8.1进行显式动力分析［M］.北京:清华大学出版社，2005.

［9］张振华，朱锡，白雪飞.水下爆炸冲击波的数值模拟研究［J］.爆炸与冲击，2004，24(2):182-188.

［10］梁龙河，曹菊珍，袁先春.水下爆炸特性的二维数值模拟研究［J］.高压物理学报，2004，18(3):203-207.

［11］柴修伟.水下炮孔爆破水中冲击波传播特性［D］.武汉:武汉理工大学，2009:62-80.