M-矩阵Hadamard积最小特征值的下界

杨晓英，刘新

（四川信息职业技术学院基础教育部，四川 广元 628017）

M-矩阵Hadamard积最小特征值的下界

杨晓英，刘新

（四川信息职业技术学院基础教育部，四川 广元 628017）

对于非奇异M-矩阵A与B，首先给出A的逆矩阵元素的范围，进而利用Brauer定理，得到B◦A－1最小特征值下界的新估计式。理论分析和数值算例说明新估计式改进了现有的结果。

M-矩阵；Hadamard积；逆矩阵；下界

M-矩阵是重要的矩阵类，有着广泛应用，物理学和经济学中的许多问题都和M-矩阵有着密切的联系。这其中关于非奇异M-矩阵B和非奇异M-矩阵A的逆矩阵Hadamard积最小特征值的下界已经成为研究的热点，并获得了一系列估计式［1－8］，本文将继续这一问题的研究，给出B◦A－1最小特征值新的下界估计式。

设N＝｛1，2，…，n｝；Rm×n（Cm×n）表示m×n阶实（复）矩阵；Zn表示所有非对角元素都为非正实数的n×n阶矩阵。

设矩阵A＝（aij）∈Rn×n，则A可以表示为A＝λI－P，其中P≥0，当λ＞ρ（P）（ρ（P）为非负矩阵P的谱半径）时，称A为非奇异M-矩阵。并记Mn为所有n×n阶非奇异M-矩阵的集合。

设A∈Mn，记τ（A）＝min｛｜λ｜：λ∈σ（A）｝，其中σ（A）表示矩阵A的谱，τ（A）称为矩阵A的最小特征值。详见文献［9］。

定义1［9］设A∈Cn×n，当n≥2时，若存在n×n阶置换矩阵P，使得

其中A11是r×r阶子矩阵，A22是（n－r）×（n－r）阶子矩阵（1≤r＜n），则称矩阵A为可约矩阵。若置换矩阵P不存在，则称矩阵A为不可约矩阵。

定义2［9］设A＝（aij），B＝（bij）∈Cm×n，用A◦B表示A和B对应元素相乘而成的m×n阶矩阵，即A◦B＝（aijbij）∈Cm×n，则A◦B称为A和B的Hadamard积。

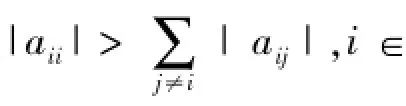
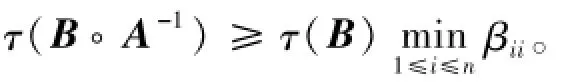
2008年，Huang［3］给出一个更为精确的估计式

其中ρ（JA），ρ（JB）分别表示矩阵A与B的迭代矩阵谱半径。

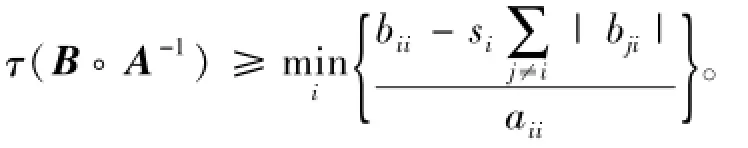
2013年，Zhou等［5］得到如下新结果：

本文将继续这一问题的研究，利用Brauer定理给出B◦A－1最小特征值的一些新的下界估计式，新估计式改进了文献［5］和其他文献中相应的结果。

1 符号与引理

为方便起见，首先给出如下符号。对于i，j，l∈N，记

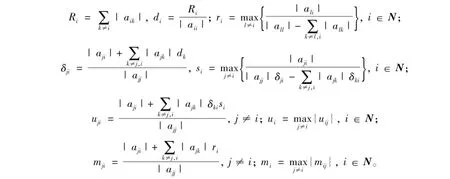
引理1［10］设A＝（aij）∈Rn×n是行严格对角占优矩阵，A－1＝（βij），则

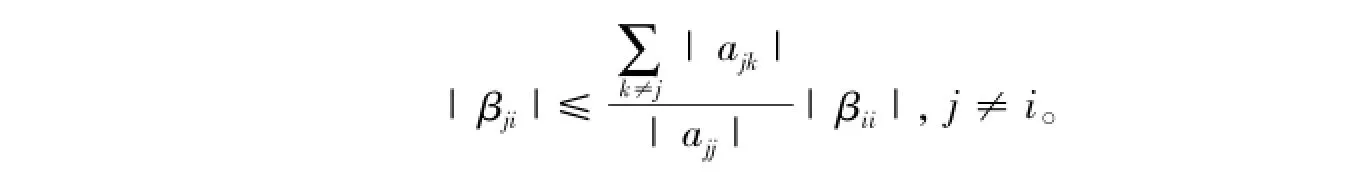
引理2［11］设A＝（aij）∈Rn×n是行严格对角占优M-矩阵，A－1＝（βij），则

引理3［2］设A，B∈Rn×n，若D∈Rn×n与E∈Rn×n是对角矩阵，则

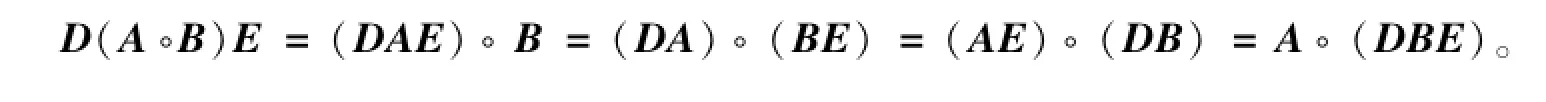
引理4［12］设A＝（aij）n×n是任意复矩阵，则A的所有特征值都位于下列区域之中

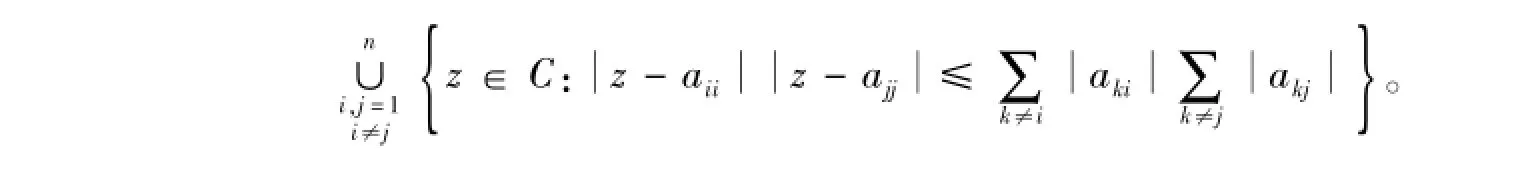
2 主要结果

定理1设A＝（aij）∈Mn是行严格对角占优矩阵，A－1＝（βij），则

证明：由A∈Mn以及符号定义，可知0≤δji＜di＜1，0≤si≤1，j≠i，i，j∈N。令

由于A是严格对角占优M-矩阵，则存在ε＞0，使得

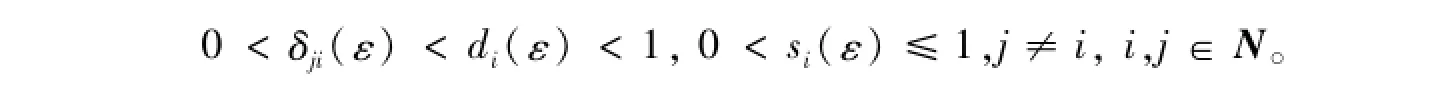
令Si（ε）＝diag（δ1i（ε）si（ε），…，δi－1，i（ε）si（ε），1，δi＋1，i（ε）si（ε），…，δni（ε）si（ε）），i∈N，则不难证明ASi（ε）也是严格对角占优M-矩阵，则由引理1可知

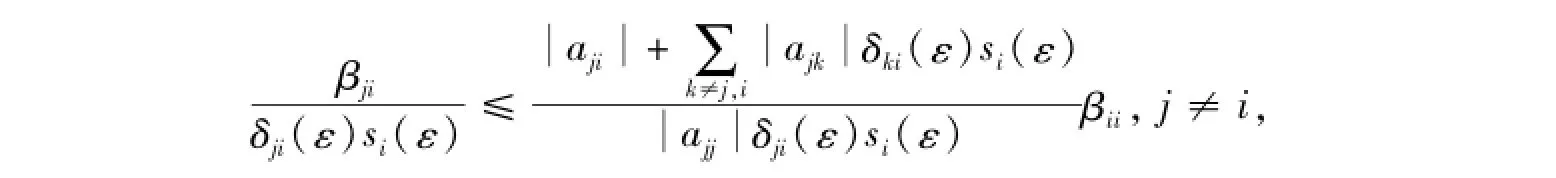
定理2设A＝（aij）∈Mn是行严格对角占优矩阵，A－1＝（βij），B＝（bij）∈Mn，则

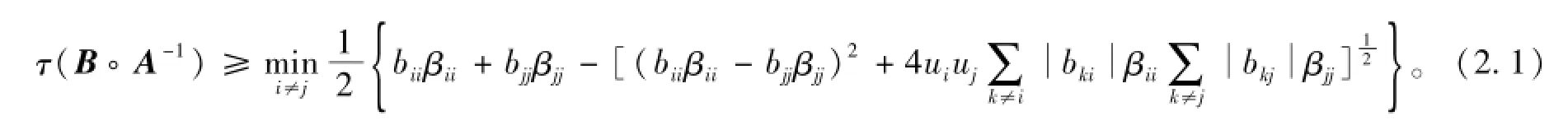
那么，存在实数ηji（0≤ηji≤1），使得

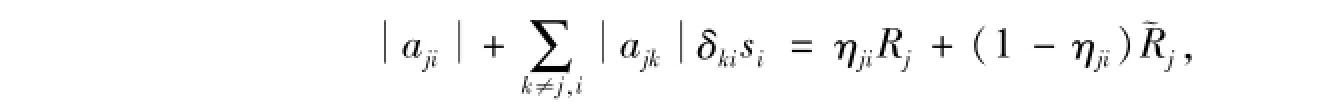
令U＝diag（u1，u2，…，un）＞0，有σ（B◦A－1）＝σ（U－1（B◦A－1）U）＝σ（U（BT◦（A－1）T）U－1），因为τ（B◦A－1）是B◦A－1的一个特征值，则τ（B◦A－1）∈σ（U（BT◦（A－1）T）U－1。令τ（B◦A－1）＝λ，由引理4知，存在数对（i，j），i≠j（1≤i，j≤n），使得

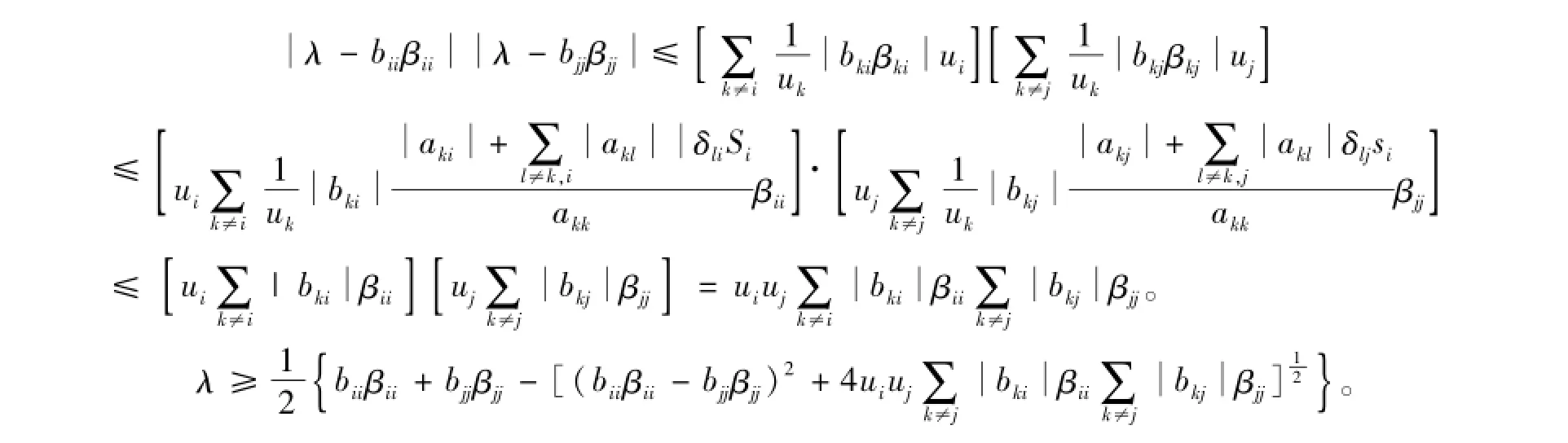
若B◦A－1不可约。令G＝（gij）是n×n阶置换矩阵，且g12＝g23＝…＝gn－1，n＝gn1＝1，其余gij＝0。则对于任意正实数ε，当ε充分小时，使得A－εG，B－εG的所有顺序主子式为正，从而A－εG和B－εG都是不可约非奇异M-矩阵，若用A－εG，B－εG代替A，B，并令ε→0，则结论仍然成立。证毕。

定理3设A＝（aij）∈Mn是行严格对角占优矩阵，A－1＝（βij），B＝（bij）∈Mn，则

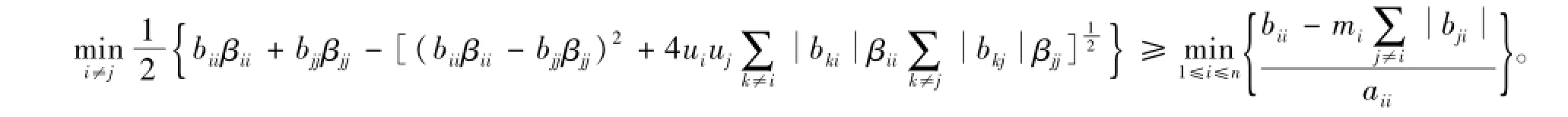
证明：不失一般性，假设

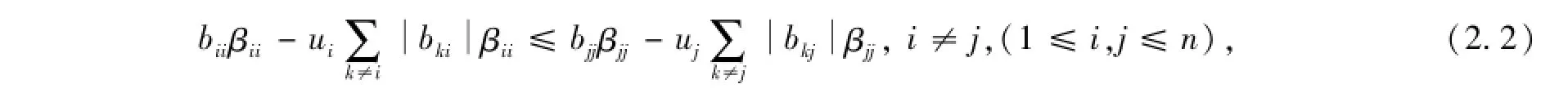
由（2.1）式与（2.3）式，得

由符号定义，可知δkisi≤ri，i≠j，（1≤i，j≤n），进而ui≤mi，i∈N，所以

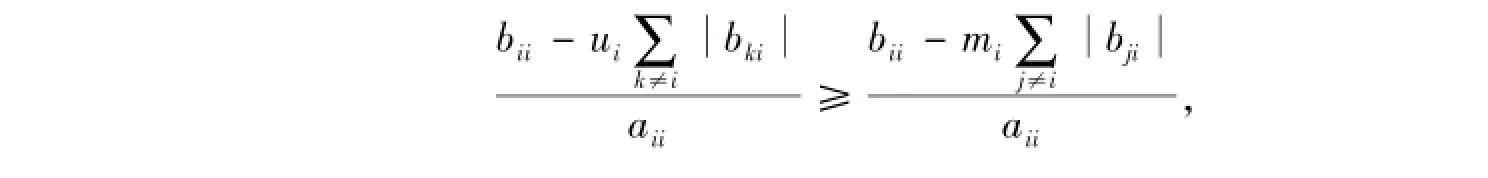
故结论成立。证毕。

定理3说明，定理2改进了文献［5］中定理4.8的结果。

3 数值算例

例1设

易知，矩阵A与B都是非奇异M-矩阵。那么

由文献［2］中定理5.7.31得τ（B◦A－1）≥0.07，由文献［3］中定理9得τ（B◦A－1）≥0.052，由文献［5］中定理4.8得τ（B◦A－1）≥0.075。应用本文的定理2，可得τ（B◦A－1）≥0.141 1。事实上，τ（B◦A－1）＝0.214 8。

通过算例分析，可知定理2的结果有效地改进文献［5］中的定理4.8和其他现有的结果。

［1］FIEDLER M，MARKHAM T L.An inequality for the Hadamard product of an M-matrix and inverse M-matrix［J］.Linear Algebra Appl，1988，101（4）：1－8.

［2］HORN R A，JOHNSON CR.Topics inmatrix analysis［M］.New York：Cambridge University Press，1991：113－115，298－299，375.

［3］HUANG R.Some inequalities for the Hadamard product and the Fan product of matrices［J］.Linear Algebra Appl，2008，428（7）：1551－1559.

［4］LIY T，LIY Y，WANG RW，et al.Some new bounds on eigenvalues of the Hadamard product and the Fan product ofmatrices［J］.Linear Algebra Appl，2010，432（2／3）：536－545.

［5］ZHOU D M，CHEN G L，WUG X，et al.On some new bounds for eigenvalues of the Hadamard productand the Fan product of matrices［J］.Linear Algebra Appl，2013，438（3）：1415－1426.

［6］陈付彬，任献花，郝冰.M-矩阵Hadamard积最小特征值的新下界［J］.数学理论与应用，2012，32（2）：60－66.

［7］刘新，杨晓英.M-矩阵Hadamard积最小特征值的新下界［J］.重庆师范大学学报：自然科学版，2013，30（2）：53－55.

［8］王峰.非奇异M-矩阵的逆矩阵和M-矩阵的Hadamard积的最小特征值下界估计［J］.应用数学，2013，26（2）：341－345.

［9］陈景良，陈向晖.特殊矩阵［M］.北京：清华大学出版社，2000.

［10］YONG X R.Proof of a conjecture of Fiedler and Markham［J］.Linear Algebra Appl，2000，320（1／2／3）：167-171.

［11］LIY T，CHEN F B，WANG D F.New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverse［J］. Linear Algebra Appl，2009，430（4）：1423－1431.

［12］BRAUER A.Limits for the characteristic roots of amatrix.II［J］.Duke Math J，1947，14（1）：21－26.

Lower bound ofm inimal eigenvalue for Hadam ard product of M-matrices

YANG Xiao-ying，LIU Xin
（Department of Basic Education，Sichuan Information Technology College，Guangyuan 628017，China）

We initially present the range of the elements of inverse matrix of A for two nonsingular M-matrices A and B．We further obtain a new estimation formula of the lower bound of the minimal eigenvalue ofB◦A－1with the theorem of Brauer．Theoretical analysis and numerical examples demonstrate that it improves the existing results．

M-matrix；Hadamard product；inverse matrix；lower bound

O151.21

A

1002-4026（2014）04-0104-05

10.3976／j.issn.1002－4026.2014.04.018

2013-07-10

四川省教育厅自然科学研究基金（13ZB0393；14ZB0442）；四川信息职业技术学院基金（2012C04）

杨晓英（1984－），女，讲师，硕士，研究方向为矩阵理论与应用。