纵向瞬态荷载下基桩的动力响应分析

2014-06-05武丹丹杨成斌王江涛

河北工程大学学报(自然科学版) 2014年2期

武丹丹，杨成斌，王江涛

（1.合肥工业大学资源与环境工程学院，安徽合肥 230009;2.安徽省金田建筑设计咨询有限责任公司，安徽合肥 230051）

低应变纵波测试因具有成本低、适用范围广等特点而得到广泛应用［1－6］。文献［1］采用分离变量法求出均匀土中有限长完整桩的瞬态桩顶竖向振动速度，为低应变桩基测试的参数反演提供了理论基础。文献［3－6］研究了桩身为有限长均匀弹性圆杆、桩半径与桩侧土剪切波速按指数型变化并考虑变截面桩中的纵波，得到桩的瞬态纵向振动解析解。本文在上述研究的基础上，根据桩周土和桩端土共同作用下基桩纵向振动的微分方程组及数值解模型，由桩身运动方程，桩顶、桩底边界条件、初始条件、构成桩土系统在瞬态激励下的定解问题，利用有限差分法解决此定解问题。对完整桩和非完整桩（缩径桩、扩径桩、断桩）时域速度曲线和速度振幅谱曲线进行归一化处理，并与理论曲线进行拟合。分析桩身、桩侧、桩底岩土参数对时域速度曲线和速度振幅谱曲线的影响，为桩身纵向瞬态动力响应分析提供理论基础。

1 桩顶纵向振动定解问题与差分解法

本文讨论纵波在桩身的传播规律，将完整桩视为等截面均质线弹性直杆，桩周土体对桩的作用简化为与位移成正比的分布弹性力和与振速成正比的分布阻尼力的组合，下面给完整桩纵向振动的定解计算方程［3］:

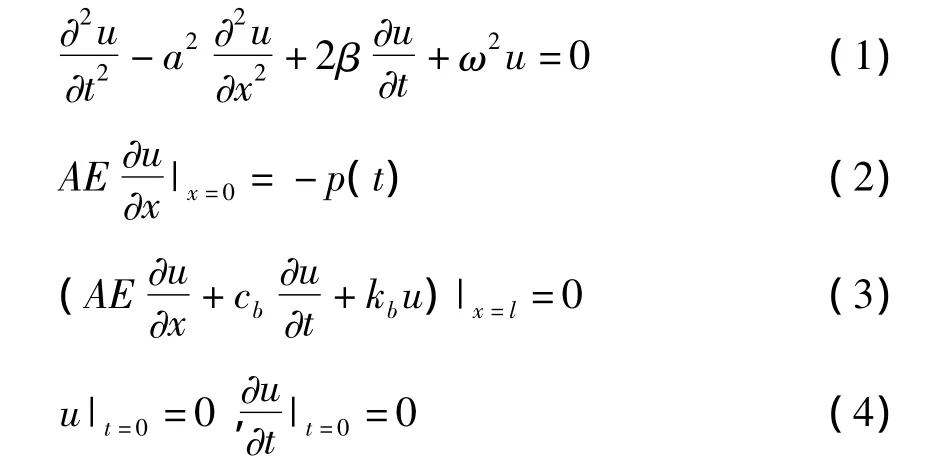
若把式（1）～（4）中的位移u（x，t）关于时间t求偏导数，即可得关于桩身质点振速v（x，t）的微分方程定解问题。

对于非完整桩，纵向振动定解方程推导过程与完整桩类似，具体公式可参见文献［5］。

采用的脉冲激振力表达式为［7］:

激振力参数和桩土参数参考反射波动测资料、工程地质勘察资料、施工记录等资料，或通过模拟实测波形确定。

一般我们采用差分数值解法来求取微分方程，将求解区域分割成M行N列的矩形网格，当给定桩土参数、激振力参数和网格参数时，便可求出网格上各节点的速度值。文献［3］和［5］详细给出了完整桩和非完整桩纵向振动定解问题的差分解法。

2 完整桩曲线拟合与理论分析

本次进行现场模拟的实验桩位于合肥工业大学纬地楼前，桩型为人工挖孔灌注桩，混凝土等级为C25。理论计算采用的主要参数:桩密度ρ=2 400 kg/m3，桩长 L=7.0 m，弹性模量E=3.250 2×1010N·m－2;桩周土密度及剪切波速:ρs=1 800 kg/m3，cb=120 m/s;泊松比 vs=0.35;桩底土密度、剪切波速及泊松比ρb=2 500 kg/m3，cb=200 m/s，vb=0.35;激振力参数取值:t0=1.25 ms，I=1 N·s 。

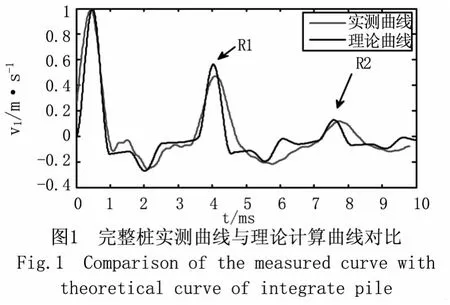
图1给出了均匀土中完整桩归一化低应变实测曲线与理论计算曲线。如图所示，最大波峰为入射波，R1为桩底反射波。一次桩底反射波R1与入射波峰值之间时间差约为3.71 ms，波速约为3 800 m/s，由公式 T=2L/Vp得桩长 L为7.05 m，与施工资料给出的7.00 m基本一致。

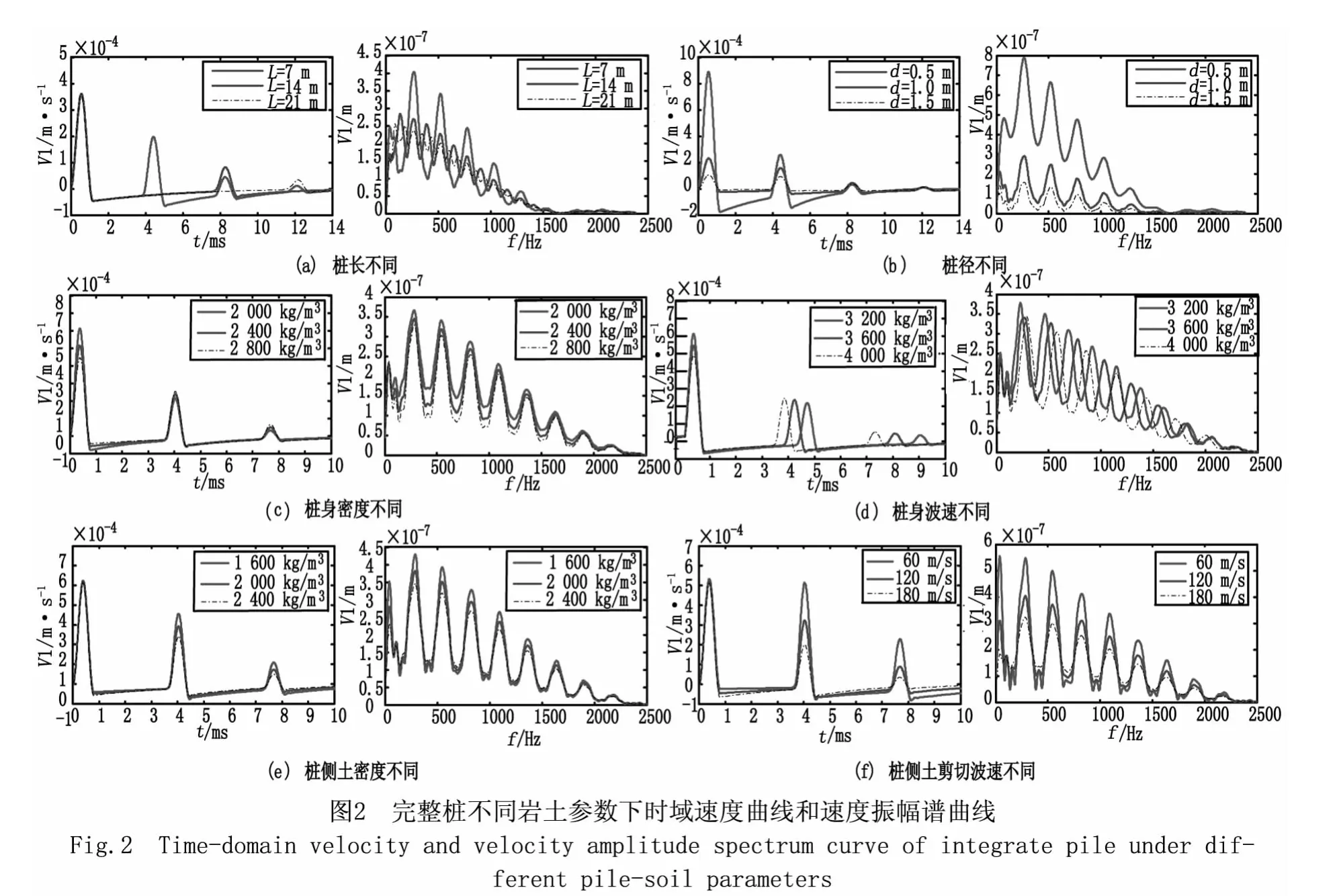
图2分别研究了完整桩桩身、桩侧土、桩底土参数对时域速度曲线和速度振幅谱曲线的影响。为了便于计算，假设基桩桩径不发生变化，为7 m，其他参数不变。

图2（a）给出了桩长L=7、14、21 m时桩顶纵向动力响应，由时域速度曲线可见，桩长加倍，一次桩底反射到达时间也加倍，各桩底反射波与入射波同相位。由速度振幅谱曲线可见，桩长一定时，随着频率的增加，速度幅值的各个峰值先增加后逐渐减小，波峰和波谷交替一次出现。随着桩长的增加，同一阶的共振峰幅值与共振谷幅值的差值（峰谷差值）减小。

图 2（b）给出了桩径 d=0.5、1.0、1.5 m 时桩顶纵向动力响应，由时域速度曲线可见，入射波幅值随桩径的增加而减小，桩底反射波到时相同，其振幅相差不大，各桩底反射波与入射波同相位;由速度振幅谱曲线可见，桩径增加，速度谱幅值减小，桩径为0.5 m的曲线上第一个共振峰很不明显，除第一个共振峰外，各阶共振峰和共振谷对应的横坐标基本相同。

图2（c）给出了桩身密度不同时桩顶纵向动力响应，由时域速度曲线可见，桩底反射与入射波均同相位，桩身密度增加时，相应的入射波和桩底反射波幅值变化都不大;由速度振幅谱曲线可见，桩身密度增大时，共振峰和共振谷幅值均减小，但共振谷幅值减小的更大些。密度增大，对第n阶共振峰的横坐标位置几乎无影响，且共振峰近乎等间隔分布。

图2（d）给出了桩身波速不同时桩顶纵向动力响应，由时域速度曲线可见，桩身波速增加，入射波峰幅值减小，桩底反射波将提前到达;由速度振幅谱曲线可见，波速一定时，除第一个共振峰外，其余共振峰横坐标随频率增加而基本等间隔分布。桩身波速增加，第n阶共振峰或共振谷向后平移，同时频差增大。

图2（e）给出了桩侧土密度不同时桩顶纵向动力响应，由时域速度曲线可见，桩侧土密度越大，波在传播过程中衰减越明显，导致桩底反射波幅值减小，但到达的时间相同;由速度振幅谱曲线可见，随着桩侧土密度增加，n阶共振峰和共振谷的横坐标基本不变，但相应的共振峰幅值减小，共振谷幅值增大。

图2（f）给出了桩侧土剪切波速不同时桩顶纵向动力响应，由时域速度曲线可见，随着桩侧土剪切波速的增加，入射波变化不大，但桩底反射波峰值减小，入射波与一次反射波之间的部分曲线会向下偏移更多，偏移越多，说明土质越硬;由速度振幅谱曲线可见，波速一定时，除第一个共振峰外，其余共振峰横坐标随频率增加而基本等间隔分布。桩侧土剪切波速增加时，n阶共振峰和共振谷的横坐标基本不变，但各阶共振峰值明显减小，共振谷值增加，峰谷差值减小。

3 非完整桩曲线理论分析

3.1 缩径桩

该模型桩为人工挖孔灌注桩，混凝土强度为C25，桩长 7.0 m，桩身半径 0.4 m，桩身密度2 400 kg/m3，浅部缩径桩的缺陷位置位于桩顶下1.0 ～1.5 m 处，缩径处的半径为 0.25 m;桩侧土上部2 m左右为填土，下部为粘土，桩底持力层为该层粘土。理论计算时，取参数为:桩周土密度ρs=1 600 kg/m3，桩周土剪切波速 vs=140 m/s，桩底土密度ρb=1 800 kg/m3，桩底土剪切波速vb=150 m/s，桩底土泊松 vb=0.35，激振冲量I=1 N·s，激振力作用时间 t0=0.78 ms。

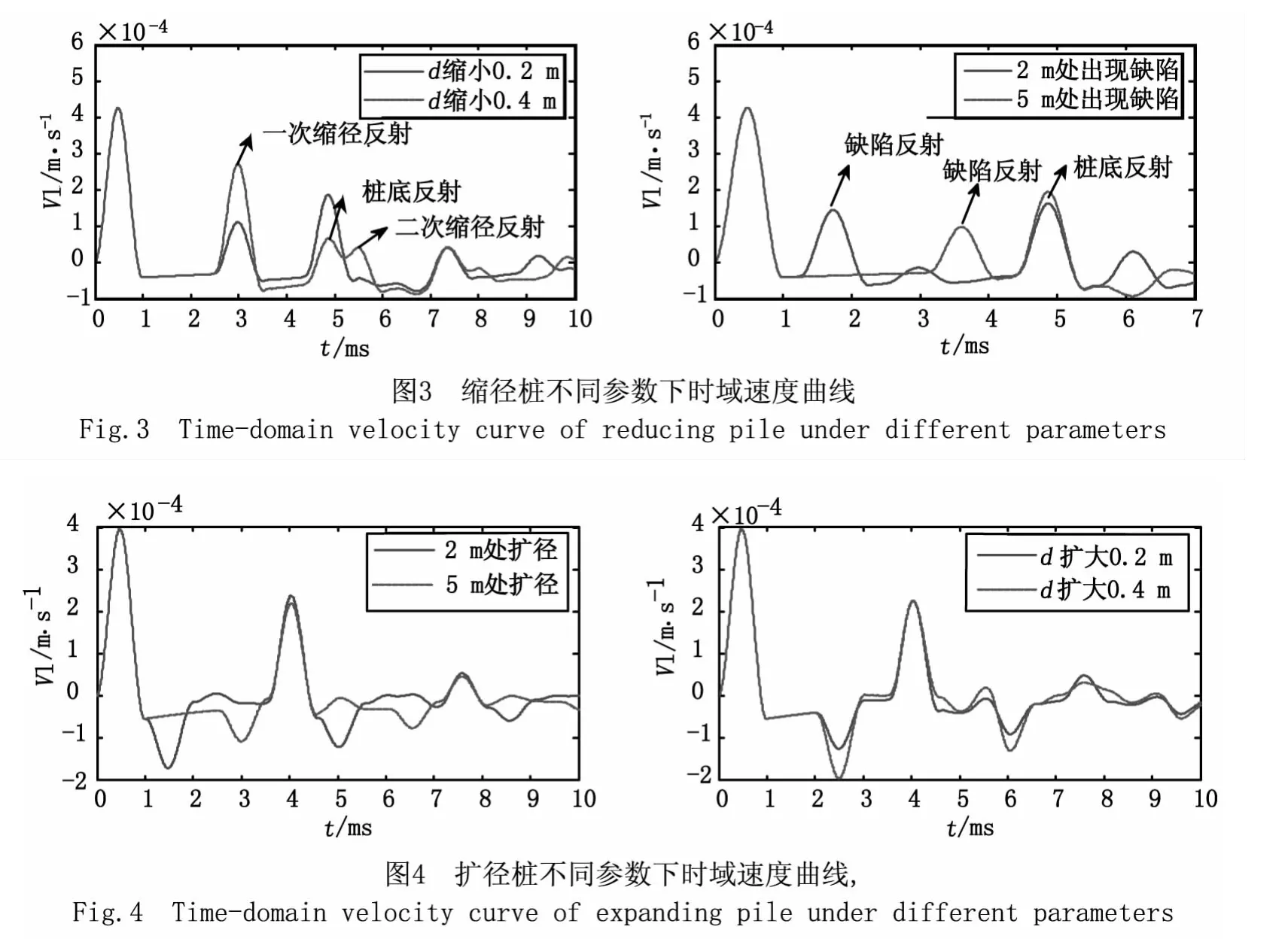
图3分析的是缩径的位置和桩径的缩小程度对时域速度曲线的影响。左图显示的是桩径缩小0.2 m和0.4 m时桩顶的时域速度曲线，由图可以看出，缩径越厉害，缩径反射越明显，桩底发射越不明显。此现象产生原因是，缩径越厉害，缩径处上下界面波阻抗相差越大，桩底处上下界面波阻抗相差越小，所以缩径反射越明显，桩底反射越不明显。只观察桩径缩小0.4 m的曲线，第一个波峰为入射波，第二个波峰为一次缩径反射，由图可知入射波峰与一次缩径反射波间时间大概为2.5 ms，所以下一个缩径反射也应相差 2.5 ms，即5.5 ms处的波峰为二次缩径反射，前面5 ms处为桩底反射，桩底反射与二次缩径反射有所重叠，所以就形成如图所示的波形图。

右图显示的是在2 m和5 m处出现缩径时桩顶的时域速度曲线，由图可以看出，缺陷出现的位置越浅，缩径反射越靠前，当缩径程度一样时，缩径反射的程度也一样，且桩底反射大小和程度都一样。

3.2 扩径桩

图4分析的是扩径的位置和桩径的扩大程度对时域速度曲线的影响。左图中桩径分别扩大0.2 m和0.4 m，由图可见，扩径处直径越大，则扩径反射越明显。这是由于扩径越厉害，扩径处上下界面波阻抗相差越大，所以扩径反射就越明显。桩底反射相差不大;右图中分别在2 m和5 m处出现扩径，由图可见，当扩径程度一样时，扩径出现的位置越浅，扩径反射越靠前，且扩径反射越明显，但桩底反射位置和程度都相差不大。

3.3 断桩

该模型桩为人工挖孔灌注桩，混凝土强度为C25，桩长 7.0 m，桩身半径 0.4 m，桩身密度2 400 kg/m3，浅部缩径桩的缺陷位置位于桩顶下约1.0 m处，缩径处的半径为0.25 m，桩侧土上部2 m左右为填土，下部为粘土，桩底持力层为该层粘土工程中，断桩的桩土系统比较复杂，在这里实际计算时，采用将断裂段的参数设计为桩侧土的参数。

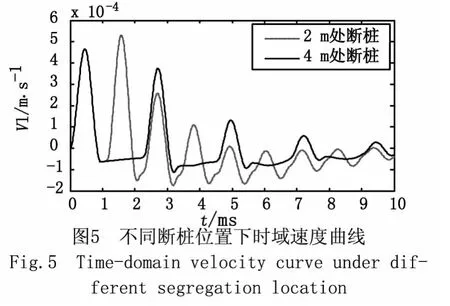
图5分析的是断桩位置对时域速度曲线的影响，分别在2 m和4 m处出现断桩，由图可知，断桩位置越浅，缺陷反射出现的越靠前，相同时间内出现的频率增加。由计算得2 m处断掉的，就相当于是2 m的桩，4 m处断掉的就相当于是4 m的桩，那么除了入射波，各个反射就是桩底反射。位置不同的断桩在相同的时间上缺陷波的大小相差不大，说明了缺陷的位置不怎么影响振动速度的衰减程度。