X射线衍射仪角度校准的光学新方法

崔建军，高思田，邵宏伟，杜 华，王鹤岩

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 中国计量科学研究院，北京 100013)

X射线衍射仪角度校准的光学新方法

崔建军1,2，高思田2，邵宏伟2，杜 华2，王鹤岩2

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 中国计量科学研究院，北京 100013)

目前X射线衍射仪(XRD)的角度检定和校准测试主要依据JJG 629—1989《多晶X射线衍射仪检定规程》和JB/T 9400—2010《X射线衍射仪技术条件》等技术文件，具体方法是采用光学经纬仪或多面棱体等进行测试，该测量方法实际应用中存在一定难度，其次测量间隔较大，不能很好反映真实的角度误差规律．为此，提出了利用 θ角和2θ角同轴并可独立运动的特点，组合采用光电自准直仪和小角度激光干涉仪等仪器，设计了一种新的XRD的角度校准方法，它能够自动快速地连续测量角度，取k=2时，扩展不确定度约1.2″．使用该方法测试能够精确得到θ和2θ轴的误差数据，可用于修正XRD测角误差，提高XRD测试精度．该方法也适用于同步辐射等大型衍射系统等其他需要角度校准的情况．

计量学；角度测量；X射线衍射；干涉测量；X射线衍射仪校准；计量校准标准

X射线衍射仪(XRD)作为重要的现代科学分析仪器，在安装时或使用一段时间后，需要对其测试性能和工作状态进行检验．而XRD测角准确度的好坏是其整机性能优劣的最重要指标之一．目前XRD的角度检测方法有几种，较精确的方法是参照 JJG 629—1989《多晶X射线衍射仪检定规程》[1]等技术文件，采用经纬仪或者多面棱体与平行光管组合测量XRD的 θ和 2θ轴的角度误差．该法测试时需将样品台卸掉，对于 2θ轴的测试甚至需要拆卸测角仪，因此不易用于已经安装的衍射仪；并且由于多面棱体的面数限制，测试间隔很大．目前使用更多的是采用各种标准物质的衍射峰对应的角度值来检验XRD的测角重复性．常用的有高纯度的Si粉末、α-SiO2等，如美国标准与技术研究院(NIST)发布的 SRM640、SRM675等标准物质[2-3]．标准物质检验测角性能易受样品本身的稳定性、纯度、粒度等影响，且与其他系统附件和测试方法等有关，测试影响因素较多，准确度较低[3]．笔者针对正在安装和对角度要求较高的衍射仪，提出采用新的光学校准方法，是对检定规程给出的光学测试方法的改进．其优点是能够准确获得θ和2θ轴的角度误差曲线，知悉其角度误差规律，找到误差限的中心范围．装调衍射仪时，通过校准θ和2θ两轴的零位，并使重合后的两轴零位位置作为仪器硬件系统的初始零位．因此，经过精确的角度校准，选择两轴误差最小的位置作为测角仪系统的零位，能够获得测角综合误差最小的工作状态．

1 测试原理装置及过程

XRD的测角仪是典型的双角度共轴的测角系统，在X射线衍射仪、同步辐射的衍射装置中应用普遍[4-5]．典型结构如图1所示的XRD测角仪，其中心部分能够独立绕转轴运动，通常称为θ角，用于安装被测样品；转轴左侧伸出的悬臂部分称为2θ角，用于安装光子探测器，也可以独立绕转轴运动.

针对此种测角系统，以校准 PANalytical公司X'Pert PRO MRD型衍射仪为例，本文提出校准方法是先采用激光干涉小角度测量法，配合高精度回转台实现对θ角的角度偏差测试；再使用光电自准直仪与高精度反射镜面实现对2θ角的测试．2θ角测试时，光电自准直仪置于衍射仪测角仪轴心上并随 θ角转动，此时以 θ角作为参考标准，并令 2θ角和 θ角转过相同的角度，可测得 2θ角相对于 θ角的角度偏差，再经过综合计算得到2θ角的角度误差．

图1 激光干涉法测量θ轴的装置Fig.1 Laser interference setup of angle θ measurement

1.1 θ角的测试过程

激光干涉小角度测量法是目前测角精度较高的一种角度测量方法[6-8]．如图 2所示，将角锥棱镜组件固定在精密转台上，再将精密转台固定在衍射仪的θ轴上，当衍射仪的 θ轴在±5°的小范围转动时，可从小角度干涉仪直接获得转角数值，当θ角继续转动时，控制转台反向转动5°作为新的测量零位，如此连续测量可实现360°的测量范围．

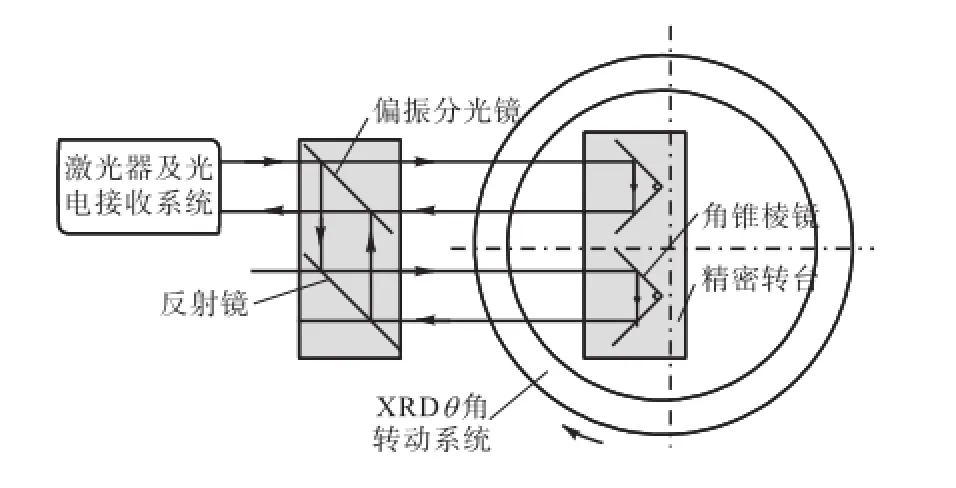
图2 激光干涉小角度测量法Fig.2 Small-angle measurement of laser interference

由于采用小角度干涉和回转台组合测量，转台实现精确定位，小角度干涉组件实现精确位置监测，最终能够实现回转角综合定位精度±1.0″(k=3)，重复定位精度0.1″．装置安装见图1．

1.2 2θ角的测试过程

自准直仪能够精确测量小角度，但无法直接大范围测量 2θ角的角度偏差[6，9]．例如 ELCOMAT3000型光电自准直仪，其测角范围最大为±1,000″，示值误差约为±0.10″～±0.25″，当测角范围不大于±20″时，示值误差仅为±0.02″．如图3所示，将光电自准直仪置于 XRD测角仪的轴心位置，将反射镜置于探测器的位置，使之随着 θ角运动，并可以跟踪 2θ角的转动．

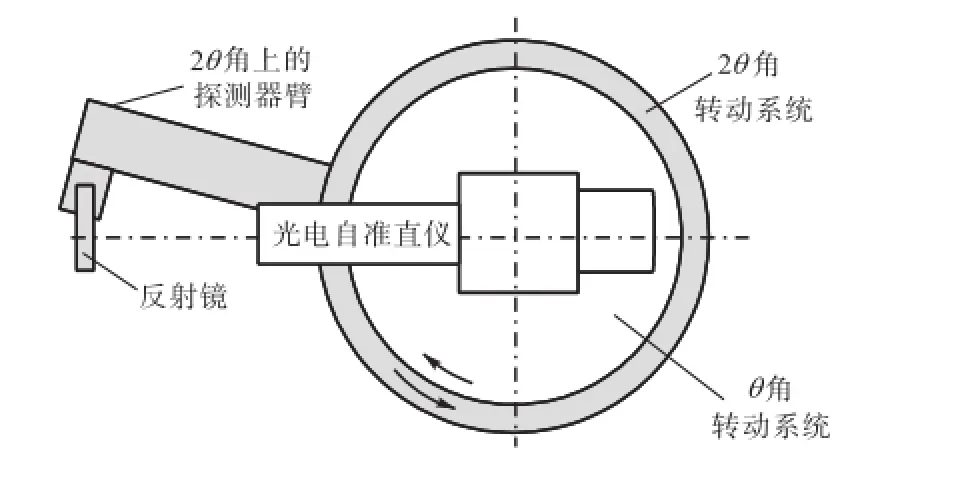
图3 自准直仪测量2θ角示意Fig.3 Diagram of angle 2θ measurement with auto collimation

如图 3所示，θ角为参考标准，光电自准直仪可测得 2θ角相对于 θ角转动时相同名义角度的角度偏差．而θ角各点的角度偏差通过激光干涉法已知，则2θ角各点的角度偏差即可算出．图4为自准直仪实际测量2θ角的照片．

图4 自准直仪测量2θ 角的照片Fig.4 Setup of angle 2θ measurement with autocollimation

2 结果分析与讨论

2.1 角度偏差的测试

分别采用激光干涉法和自准直法测量 θ角和2θ角的角度偏差，测量范围为测角仪θ角的最大转角范围，测量采样间隔最小能够小于测角仪的最小步距0.000,1°．实验中选择采样间隔 0.03°，获得了准确连续的误差特征曲线，其主要误差符合周期正弦规律．

如图5和图6所示，在角度范围0°～6°内，θ角的角度误差约为±15″，2θ角的角度误差在-10″～6″之间，二者的误差周期均为0.50°．

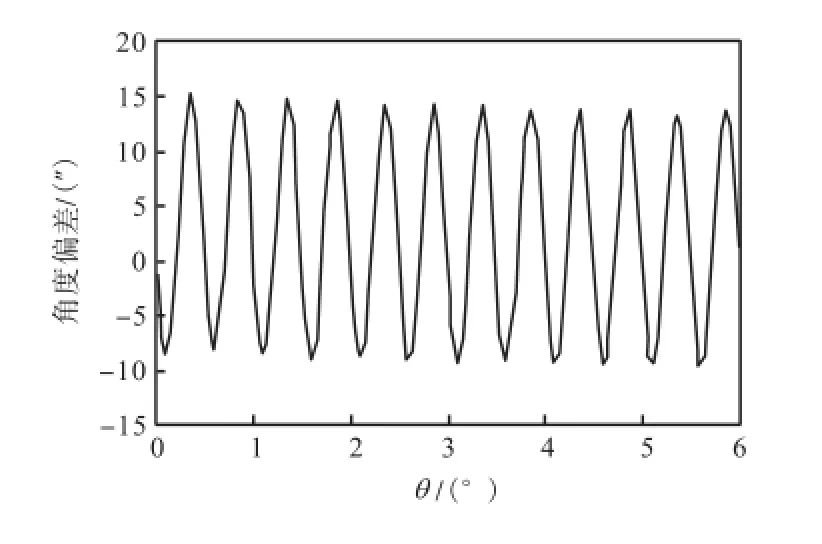
图5 θ 轴角度误差曲线Fig.5 Angle error curve of θ axis

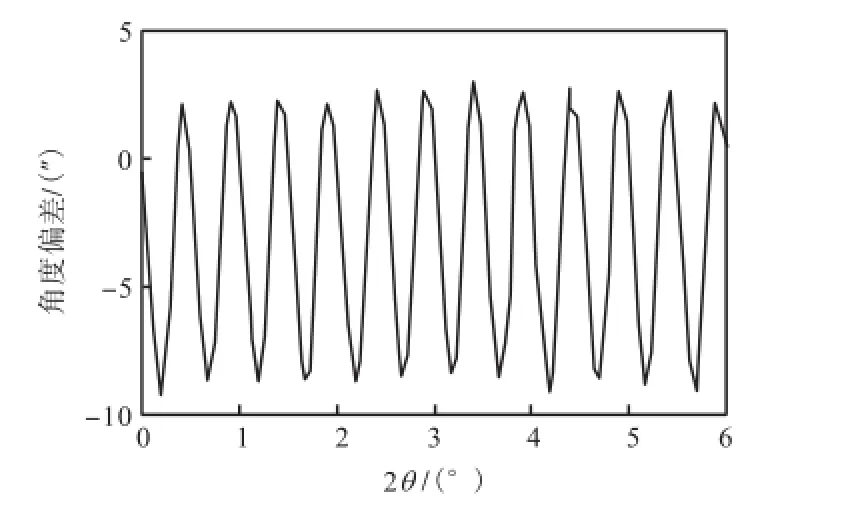
图6 2θ 轴角度误差曲线Fig.6 Angle error curve of 2θ axis

参照JJG 629—1989[1]采用多齿分度台与多面棱体组合测量，实现的测角间隔为 0.920 7°，测角范围为0°～100°，分别对θ角和2θ角进行了测试，测试误差曲线如图7和图8所示．

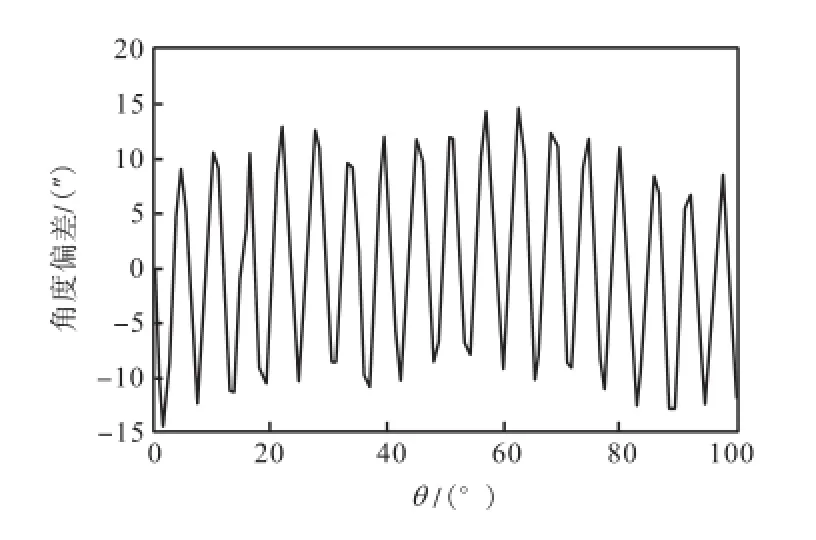
图7 多面棱体等测得的θ轴角度偏差Fig.7 Angle error curve of θ axis measured with polygon

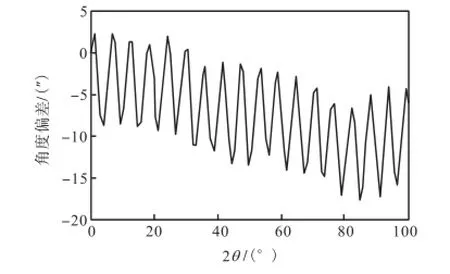
图8 多面棱体等测得的2θ 轴角度偏差Fig.8 Angle error curve of 2θ axis measured with polygon

由图 7和图 8可知，与新方法测得结果基本一致，而误差周期约为 5°，不是测角系统实际的误差周期．

2.2 误差拟合与修正

由于角度偏差具有明显的正弦规律，因此对图 5和图 6的误差曲线进行拟合计算，为了说明问题，给出 θ角在 6°范围内的拟合方程(拟合曲线见图 9和图10)为

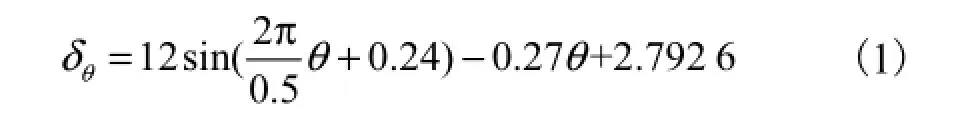
2θ角在6°范围内的拟合方程为

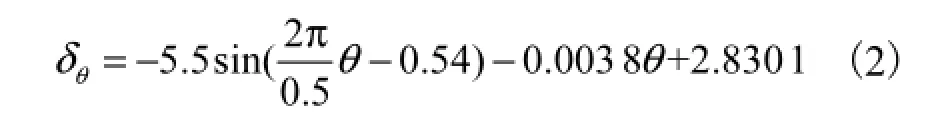
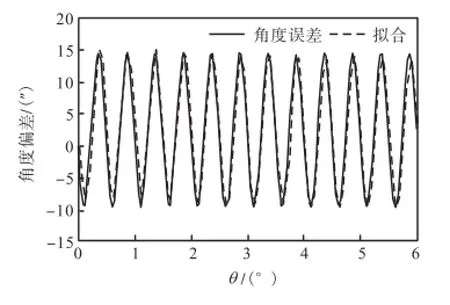
图9 θ轴角度误差及其拟合曲线Fig.9 Angle error of θ axis and its fitting curve

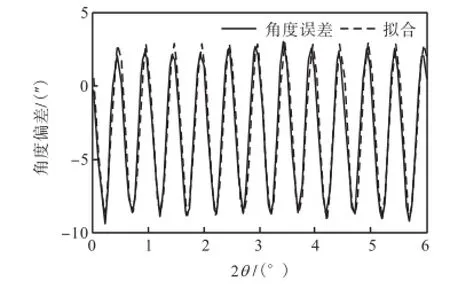
图10 2θ轴角度误差及其拟合曲线Fig.10 Angle error of 2θ axis and its fitting curve

将各角度位置对应的偏差采用拟合曲线进行逐点修正，修正后的角度误差降低到±2″，测角残差曲线如图11和图12所示．

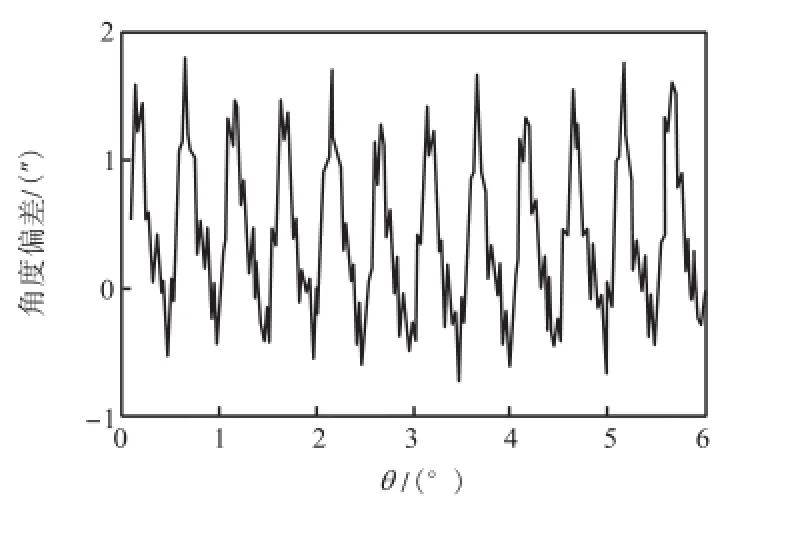
图11 θ 角拟合修正后的残差Fig.11 Residual error of θ axis after fitted

2.3 测量误差量值及来源

测角仪的测量误差来源主要有θ角和2θ角的光栅角度编码器引入的圆周分度间隔误差和光栅刻线误差、系统装配引入的同轴度误差以及初始零位误差和环境温度漂移等导致的测角误差．以被测 XRD的测角误差为例，误差量值估算如表1所示．

各角度对应的角度误差是以上几种误差的综合表现效果，可以依据拟合曲线，建立角度误差补偿数据集，并在实际测量中对原始数据中的角度值进行修正，从而提高测量数据的准确度．

通过精密角度校准后，可选择角度测量零位处于正弦偏差的中心位置，使得各点角度最大角度偏差最小，例如±18″即±0.005°．若初始零位选在角度偏差最大的位置，则最大角度偏差能够达到 36″或者-36″即±0.01°．结合实验调节误差等的引入，综合的测角偏差则更大．这还不包括 XRD实际测试过程中，样品调节和光路偏差等引入的测量误差．测量结果仅是测角仪本身的精度评定．

2.4 精度评定方法的讨论

通常参照 JJG 629—1989[1]评定 XRD测角仪性能．衍射仪的测角性能用单向测角准确度、单向测角复现性以及 2θ角的单向测角重复性进行评定．而JJG 97—2001《测角仪检定规程》中关于常规测角仪的性能评价则是通过示值误差、测量重复性以及空程等概念描述．对于具有测量功能且可精确定位的回转运动系统，则用定位精度和重复定位精度等术语定义其测量及执行性能．

其次，JJG 629—1989提出的单向测角复现性计算方法，与JJF 1001—2011《通用计量术语及定义技术规范》中关于复现性术语的描述及其复现性测量条件的定义，也有较大区别．

另外，在 JJG 629—1989中，评定单向测角准确度时，规定每隔 5°测量 1次，取其中的最大误差Δθmax来表示．由实验可知，测量间隔 5°恰是角度偏差周期0.5°的倍数，即所有测量值均为误差曲线的同相位点，因而测得结果会优于实际精度．

为避免测量间隔与误差周期相关，采用 23面的多面棱体等，如图7和图8所示，虽然粗略得到了最大的角度偏差值，但没有反映出真实分度误差的周期，这是由于测量间隔太大造成的．

3 测量不确定度评定

经分析主要有如下几项误差来源对测量结果有影响：激光小角度干涉系统及精密转台组成的测量装置 x1示值 αs引入的不确定度 U(x1)，装置安装的偏心误差 x2引入的不确定度 U(x2)，光电自准直仪 x3示值 βs引入的不确定度 U(x3)及其安装的偏心误差x4引入的不确定度U(x4)，环境温漂x5等引起θ角的变化量引入的不确定度 U(x5)及二者的重复性 x6和x7引入的不确定度U(x6)与U(x7)．对θ角示值α的偏差计算模型(式(3))求导得θ角不确定度分量的灵敏系数均为1．

2θ角示值β的偏差计算模型为

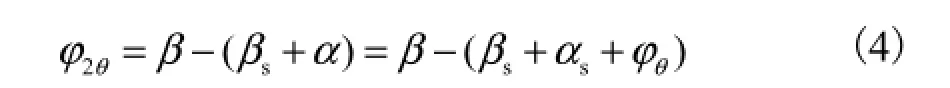
同理可得2θ角不确定度分量的灵敏系数均为1．

在实际使用环境中，温漂在±1,℃范围内，经多次测试可知，θ角的示值变化范围小于 0.3″，当 α=β时，因温漂 2θ角相对于θ角的变化量引入的不确定度小于0.05″，可忽略不计．总的温度影响均按1,℃内最大变化量进行不确定度分析，因此灵敏系数也均取1，即各分量不相关．

由表2得到θ角的合成不确定度为

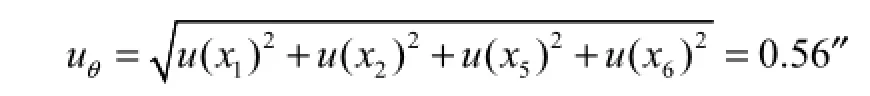
取包含因子k=2得到扩展不确定度Uθ=1.2″．

2θ角的合成不确定度为

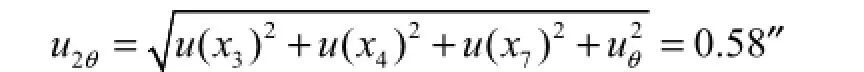
粗略估计，取包含因子k=2得到U2θ=1.2″．

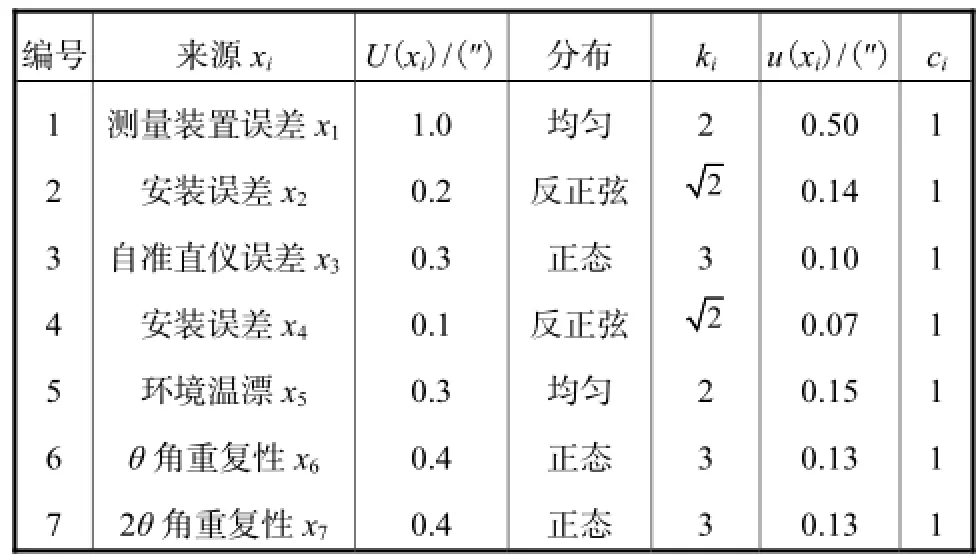
表2 角度校准的标准不确定度分量Tab.2 Standard uncertainties of angle calibration

4 各种测角方法的比较

在各种 XRD角度测量方法中，光学方法的测量精度较高，例如采用经纬仪和多面棱体，或多面棱体和多齿分度台等的组合法，或本文的测试方法．各种测角方法的具体分析比较见表3．

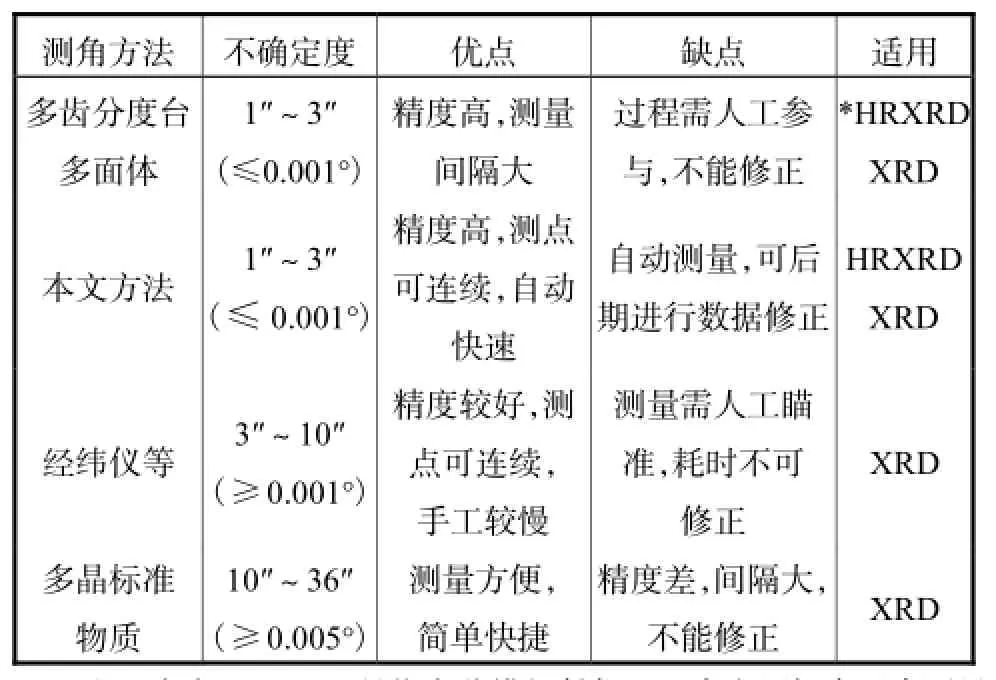
*注：表中HRXRD是指高分辨衍射仪，通常应用场合要求测量精度较高．

其次，利用单晶晶格和多晶粉末等标准物质的衍射峰位来判断衍射仪的测角性能也很常用．它通过测量衍射仪的实际衍射峰位，与理论峰位参考值进行比较，从而得到衍射仪的测角准确度．这要求所参考的标准物质的衍射峰位准确度高于被测XRD的测角准确度．若采用光学法修正后的XRD，测角不确定度可从0.01°(36″)提高到0.001°内，则该XRD能够对标准物质的实际衍射峰位进行校准．校准后的标准物质衍射峰位的准确度约为0.003°，则该标准物质可以校准测角准确度不大于0.01°的多晶XRD．以往具有高准确度参考峰位值的标准物质一般溯源至 NIST的晶格比较器(其测角不确定度约为 3″)上[2，10-12]．应用本文提出的测角方法，对 XRD测角仪进行修正后，可使被测XRD也具有相当的测量能力．

5 结 语

本文提出的测量方法和综合测量方案校准 XRD的测角精度，不仅能够实现连续角度测量，采样间隔细密，测量精度高，速度快．该方法的校准装置安装方便，测量过程实现自动化，避免了人为干扰．突出特点是能够依据 θ和 2θ角的误差曲线特性，来精确校准角度零位，使系统测角综合误差降至最小．该方法校准后衍射仪能够实现最佳工作状态，这是其他方法实现不了的．

该方法也能够用于在多角度共轴系的测量系统的角度校准．其中衍射仪是较为典型的应用，也可以用在同步辐射小角衍射装置等类似的角度测量系统的校准，以及多角度实时联动系统的角度校准．

参考文献：

［1］ JJG 629—1989 多晶 X 射线衍射仪检定规程[S]. 1989. JJG 629—1989 The Verification Regulation of Polycrystalline X-Ray Diffractometer[S].1989(in Chinese).

［2］ Freiman S W，Trahey N M. Certificate：Standard Reference Material 640c[S]. Gaithersburg，MD USA：National Institute of Standards and Technology，2000.

［3］ 马礼敦. X射线粉末衍射仪性能的评估[J]. 上海计量测试，2007，34(2)：15-18.

Ma Lidun. Performance estimation of X-ray powder diffractometer [J]. Shanghai Measurement and Testing，2007，34(2)：15-18(in Chinese).

［4］ Kubicek K，Braun J，Bruhns H，et al. High-precision laser-assisted absolute determination of X-ray diffraction angles[J]. Review of Scientific Instruments，2012，83(1)：013102-013108.

［5］ Palermo R N，Short S M，Anderson C A，et al. Determination of figures of merit for near-infrared and Raman spectrometry by net analyte signal analysis for a 4-component solid dosage system [J]. Journal of Pharmaceutical Innovation，2012，7(2)：56-68.

［6］ 黄银国，林玉池，王 为，等. 基于互相关分析的激光自准直小角度测量技术[J]. 纳米技术与精密工程，2010，8(2)：120-125.

Huang Yinguo，Lin Yuchi，Wang Wei，et al. Laser autocollimation measurement of small angle based on cross correlation [J]. Nanotechnology and Precision Engineering，2010，8(2)：120-125(in Chinese).

［7］ 何 川，林家明，邹桂兰，等. 双频激光干涉测角中角锥镜的不对称性对测角精度影响的分析[J]. 光学技术，2007，33(增1)：289-290，292.

He Chuan，Lin Jiaming，Zou Guilan，et al. Effect of optical corner cubes’ asymmetry on angle measurement [J]. Optical Technique，2007，33(Suppl 1)：289-290，292(in Chinese).

［8］ 舒 阳，邱 易，羡一民，等. 激光角度干涉仪测量精度的几个影响因素[J]. 工具技术，2008，42(5)：72-74.

Shu Yang，Qiu Yi，Xian Yimin，et al. Influence factors on measuring precision of laser angular interferometer [J]. Tool Engineering，2008，42(5)：72-74(in Chinese).

［9］ Šiaudinytė L，Bručas D，Rybokas M，et al. Polynomial error approximation of a precision angle measuring system [J]. Geodesy and Cartography，2013，39(1)：7-10.

［10］ Blanton T，Huang T，Toraya H，et al. JCPDS—international centre for diffraction data low-angle powder diffraction study of silver behenate[C]// Advances in XRay Analysis. USA，1995：99-105.

［11］ Wong-Ng W，McMurdie H F，Hubbard C R，et al. JCPDS-ICDD research associateship(Cooperative program with NBS/NIST)[J]. Journal of Research of the National Institute of Standards and Technology，2001，106(6)：1013-1028.

［12］ Byun S H，Prestwich W V，Chin K，et al. Efficiency calibration and coincidence summing correction for a 4 NaI(Tl)detector array[J]. Nuclear Instruments and Methods in Physics Research，2004，535(3)：674-685.

(责任编辑：赵艳静)

New Optics Calibration Method for Goniometer of X-Ray Diffractometer

Cui Jianjun1,2，Gao Sitian2，Shao Hongwei2，Du Hua2，Wang Heyan2
(1. State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China；2. National Institute of Metrology，Beijing 100013，China)

In China，the goniometer calibration for X-ray diffractometer is mainly referred to JJG 629—1989《Verification Regulation for Polycrystalline X-Ray Diffractometer》and JB/T 9400—2010《Specification for X-Ray Diffractometer》. Optical theodolite and polygon are used to test goniometer，but these methods are complex and hard to test. So a new optics calibration method is presented, which can automatically measure the angular misalignment of the θ axis and 2θ axis with very small steps. The measuring system is composed of photoelectric autocollimator and small-angle laser interferometers，and the measure uncertainty is about 1.2 arc seconds(k=2). The whole set of angular error records obtained can be used to compensate for angular misalignment in future calculations. This method is also suited for calibrating the angular error of twin axial measure system.

metrology；angle measurement；X-ray diffraction；interforometer；X-ray diffractometer calibration；metrology and calibration standards

TH89

A

0493-2137(2014)08-0747-06

10.11784/tdxbz201212014

2013-01-09；

2013-06-13.

国家自然科学基金重点资助项目(91023021)；中国计量科学研究院基本业务费资助项目(AKY0703)和自筹基本业务费资助项目(24-JB1104)；机械设计及理论浙江省重中之重学科和浙江理工大学重点实验室开放基金资助项目(ZSTUMD2012A005).

崔建军（1977— ），男，博士研究生.

崔建军，cuijj@nim.ac.cn.

时间：2013-11-04.

http://www.cnki.net/kcms/detail/12.1127.N.20131104.1415.002.html.