胫骨捷联惯性导航的人员行进距离估计
2014-06-05汪少初刘开华
汪少初,刘开华,刘 昱
(1. 天津大学电子信息工程学院,天津 300072;2. 天津市测绘院,天津 300381)
胫骨捷联惯性导航的人员行进距离估计
汪少初1,2,刘开华1,刘 昱1
(1. 天津大学电子信息工程学院,天津 300072;2. 天津市测绘院,天津 300381)
研究了惯性测量单元(IMU)固连在人员胫骨中间的行走步长计算方案,提出了捷联惯性导航算法中零速率修正(ZUPT)时刻导航参数的重置方法,准确得到了以初始方位角为未知数的三维位移函数表达式,避免二重积分对近似误差的扩散.通过分析人员行进特性并结合 ZUPT时刻胫骨与路面垂直的关系,以每步中垂直地面方向的位移几乎为零作为约束条件,解算另外两个平行地面方向的位移,进而计算每一步的步长.该方法针对不同的人员和行走环境无需修改相关参数,有较好的适应性和通用性.经多人次行走实验验证,行进距离计算误差在 8%以内的概率为91%.
捷联惯性导航;零速率修正;行人航位推算
近年来,行人航位推算(pedestrian dead-reckoning,PDR)作为室内人员定位的一种解决方案,成为研究热点[1],其中,将低成本的惯性测量单元(inertial measurement unit,IMU)固连在人员身体上,利用捷联惯性导航方法计算行进方向和步长,再以步长作为最小位移单元来推算人员行进轨迹的方法得到了广泛的研究和应用.该方法无需在待定位的环境中布置额外的参考设备并进行大量的前期测量[2],系统简单且通用性好.然而,IMU的测量误差、捷联惯性导航固有的累积误差和坐标系转换偏差等误差源严重影响步长计算的精度.无相关改进算法的情况下,这些误差源将使定位系统的累积误差在 1,min内超过100,m[3].文献[4]也提到,利用精度相对较高的战术级惯性传感元件,按照捷联惯性导航的一般计算方法,30,min内位移误差达到 1,131,km(约 1/6地球半径),而利用消费级惯性传感元件计算的位移误差更是达到1个地球半径.
随着微机电系统(micro-electro-mechanical sys-tems,MEMS)技术的发展和生产工艺的改善,低成本IMU的测量精度越来越高[5].因此,如何减小系统固有的累积误差和坐标系转换偏差,提高步长计算精度成为研究难点.
在基于惯性导航的 PDR算法研究中,文献[6-9]均采用零速率修正(zero velocity update,ZUPT)的方法,将导航计算截断在一系列相对较短的时间段内,以相邻两个 ZUPT点作为一个导航周期的开始和结束点.在导航周期的起始时刻,定位系统重置导航参数,如初始速度和 IMU机体坐标系与目标坐标系间的初始方位角.在该导航周期内利用惯性导航原理计算行进的位移,进而控制累积误差的无限扩散.文献[10]将 IMU绑定于脚尖,通过惯性数据特性寻找行进过程中的准静止状态,以该状态对应时刻为ZUPT点,认为此时测量的加速度仅为重力加速度,利用重力加速度在IMU三轴的分量,得到IMU的初始方位角,重置导航参数.但是,脚尖较小的扰动或准静止状态的不准确均会导致初始方位角存在一定的偏差,后续每一时刻方位角的计算均建立在这个存在偏差的初始方位角之上,使导航方程中重力加速度的去除过程产生较大的误差,导航计算的位移误差随时间不断累积并有发散趋势.
文献[11]将 IMU置于腰间,利用行进过程中腰部运动符合倒立摆模型的特点寻找ZUPT点,计算腰部在垂直方向上的最大和最小位移,利用几何比例关系得到步长.该方法对最大和最小位移的计算精度要求较高,较小的偏差导致步长计算误差成倍地增大.并且针对不同的人员,需要设定腿长和相应的比例因子,通用性较差.文献[12]将 IMU置于胫骨中间,认为行走过程中胫骨运动符合倒立摆模型,仅在前进方向和垂直方向运动,用两轴加速度和单轴角速度实现步长计算,忽略行走过程的三维运动特性.当行走过程不符合倒立摆和二维运动模型时,加速度的坐标系转换将存在较大的偏差,导致重力加速度的去除过程发生错误.此外,该方法对行走方式有很高的要求,局限性较大.文献[11-12]均通过倒立摆模型寻找ZUPT点,仅靠高要求的绑定位置简单地将初始速度和方位角重置为零.然而,初始方位角作为导航计算的基准,其准确性直接影响步长计算的精度,较小的偏差将导致重力加速度的去除过程产生较大的误差.初始方位角的偏差是坐标系转换偏差的主要因素.
本文在文献[12]的基础上,详细分析了行走时胫骨的运动过程,充分考虑行走过程的三维特性,提出了一种在 ZUPT时刻初始方位角的重置方法.不直接地将初始方位角设定为零或某一固定数值,而是将初始方位角设定为未知数,导航计算每一步在三轴方向上的位移函数关系式.无近似地去除重力加速度,将重力加速度去除过程产生的误差从重积分里剥离开来.利用ZUPT时刻胫骨与地面垂直这一特性,以垂直路面方向的位移几乎为零作为约束条件,结合行走过程的三维特性对位移进行适当的近似和修正,解算出平行于路面的其他两个方向上的位移,进而计算步长并进行总位移的累加.本方法避免了二重积分对重力加速度去除误差的扩散,大大提高了步长计算的精度.提出的算法方案对人员的行进方式和行进路面没有特殊要求,对不同的人员无需进行相关的参数设置,具有较强的适应性和通用性.
1 捷联惯性步长计算
本文以人员行进的每一步步长作为最小位移单元对人员行走距离进行估计,步长计算的精度直接影响行走距离的精度.结合行走过程测量的惯性参量,对人员行走时胫骨的运动过程进行详细分解,找到胫骨与地面垂直时惯性参量的特性,依此寻找 ZUPT点.利用 ZUPT点将连续的行进过程分为若干单步过程,以每个单步持续的时间为一个导航周期,利用捷联惯性导航原理计算步长.
1.1 行走过程胫骨运动分析
本文将 IMU安置于右脚胫骨中间外侧位置,尽量保证人员在解剖学姿势站立时,IMU机体坐标系Oxbybzb与当地坐标系 Ox(F)y(R)z(D)重合,如图 1所示.xb轴指向 IMU机体的正前方,yb轴指向机体的正右方,zb轴指向机体的正下方.x(F)轴指向人员行进的正前方,y(R)指向人员行进的正右方,z(D)轴垂直向下指向地心,与当地重力加速度方向一致.
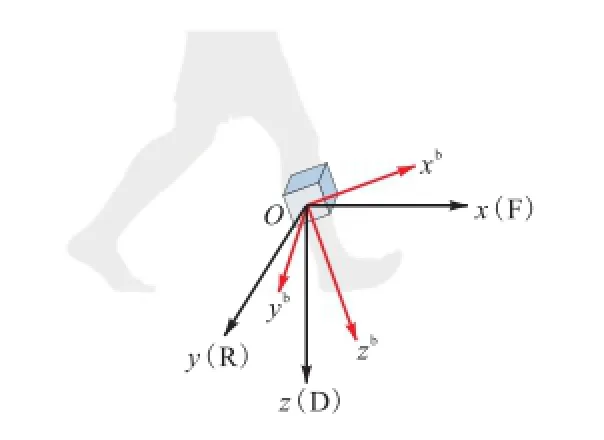
图1 IMU的安置位置Fig.1 Position of IMU mounted
文献[11]给出了行走姿势和动作的分解图.在其动作分解的基础上,将行走过程中测量得到的惯性数据与之对应.为更直观地展现行走过程中胫骨运动的三维特性,图2给出几个典型的IMU位置及坐标系 Oxbybzb与 Ox(F)y(R)z(D)的相对位置,与动作分解对应的惯性数据为某测试人员匀速行走时,测量得到的 IMU机体坐标轴 xb、yb和 zb的角速度信号.由图解可知,人员在行走过程中,左脚和右脚分别经历的动作和状态基本一致,包括脚面完全贴地(flat foot)、脚跟抬起(heel lift)、脚尖离地(toe off)、脚跟着地(heel strike)等.持续的行走过程可认为左脚和右脚周期性地重复这些动作,重复周期为人员向前行进 1步所需的时间.本文后续提到的 1步指左脚和右脚均向前迈进 1步.人员匀速行走时,可认为相邻两步持续的时间和步长基本相同.变速行走时,所测得的三轴角速度信号波形与图 2类似.随着人员行进步伐的不断重复,测得的惯性参量也周期性地重复,且每步持续的时间和参量大小也基本相同.因此,无论人员匀速还是变速行走,只需准确判别行走过程所包含的动作和状态即可区分每一步.
本文利用IMU机体坐标系yb轴角速度信号检测行进过程中所有胫骨垂直地面的时刻(shank vertical point,SVP),即图 2中 t1和 t10.该时刻yb轴角速度信号接近零且胫骨相对地面静止,对应的胫骨运动速度也可近似看作零.因此,t1和t10可作为行走过程的ZUPT点,作为每一步的起始和结束点,将行走过程分割为若干单步.
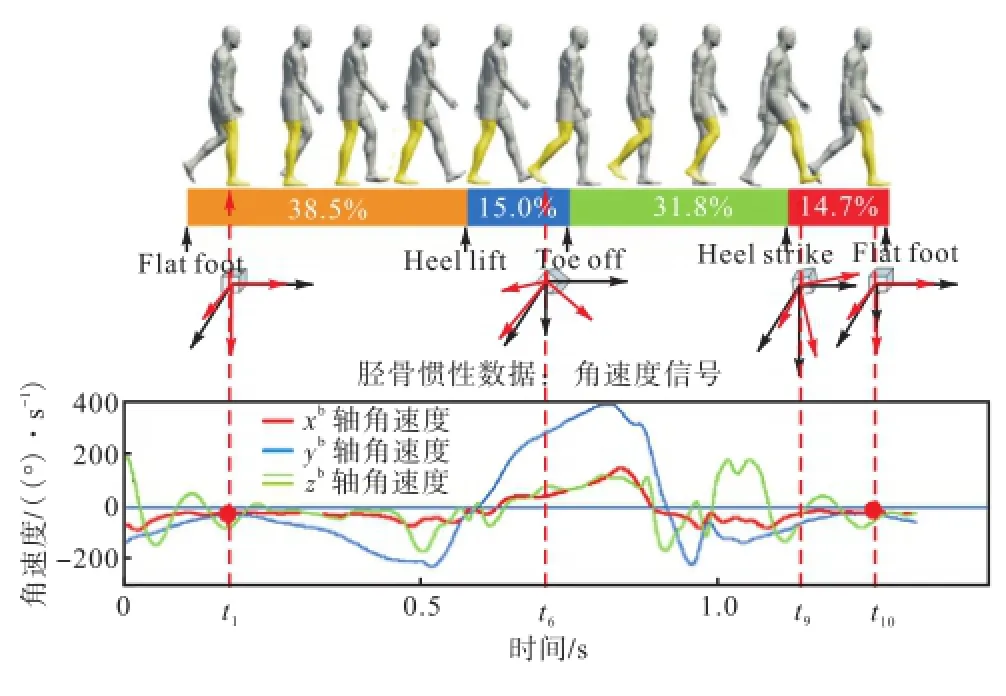
图2 人员行走过程分析Fig.2 Analysis of pedestrian walking
1.2 胫骨捷联惯性步长计算方法
根据上述对胫骨运动过程的分析,将行走过程分为若干单步.在每一步内,ZUPT点作为导航周期的起始,运用捷联惯性导航原理计算行进步长.图 3为捷联惯性导航系统原理.
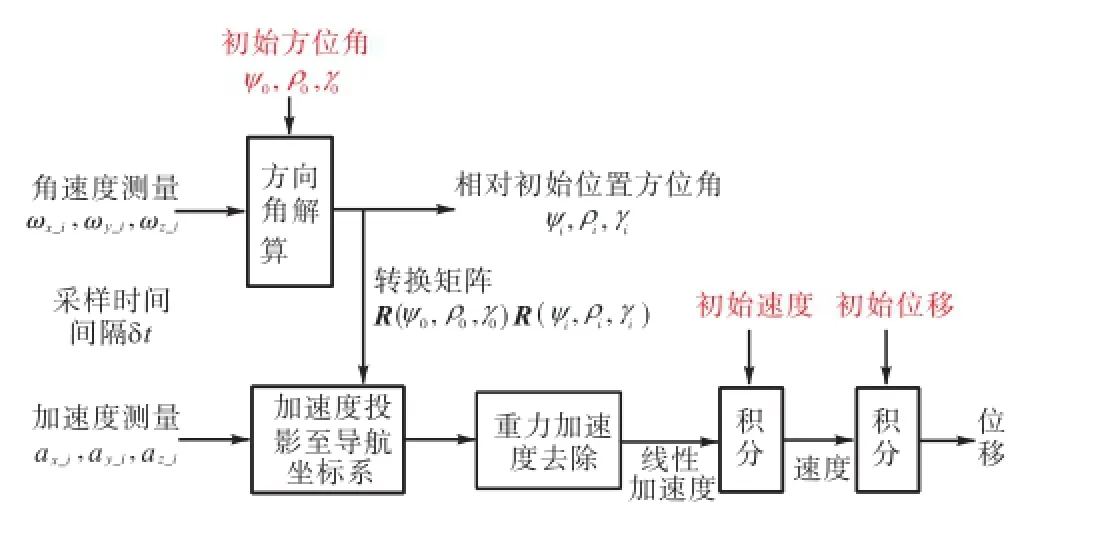
图3 捷联惯性导航系统原理示意Fig.3 Block diagram of strap-down inertial navigation system
t1时刻Oxbybzb到Ox(F)y(R)z(D)的转换矩阵为即假设初始方位角为若 IMU在胫骨处绑定位置足够好(使两坐标系完全重合),则初始方位角全为零.但行走人员不同,每次绑定的位置和方式也不完全一致,很难做到两坐标系完全重合,因此本文考虑更一般的情况.
人员行走过程中,IMU测得其机体坐标系下三轴角速度为_xiω 、_yiω 和_ziω ,加速度为_xia 、_yia 和az_i,采样周期为 δt,i为采样时间点.假设 i时坐标系 Oxbybzb对应位置到 t1时刻 Oxbybzb对应位置的转换矩阵为文献[10]给出其迭代关系为
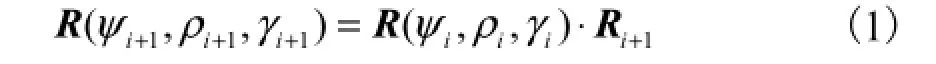
其中
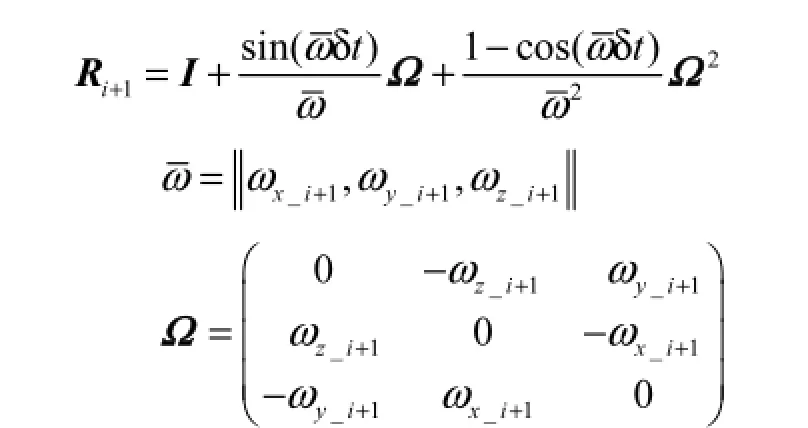
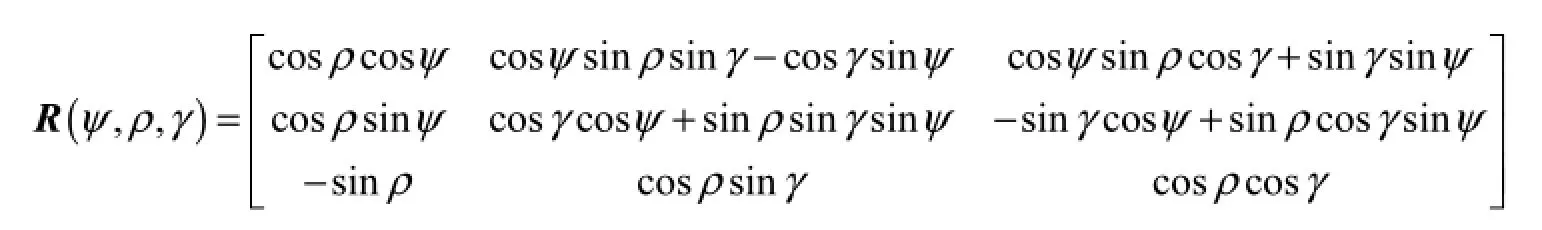
为了简化公式的表达,引入Ω这一中间变量,其物理意义为 i到 i+1时刻转换矩阵R的改变量.因此,在 Ox(F)y(R)z(D)坐标系下,捷联惯性导航方程为
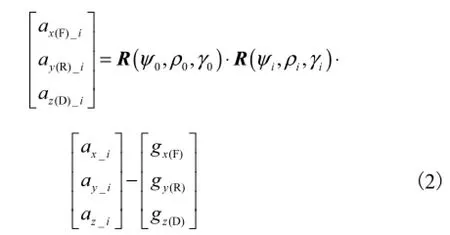

2 ZUPT点初始方位角解算及改进步长计算
图2中t1和t10时刻为SVP点,作为捷联惯性导航步长计算的起始点,IMU机体坐标系 Oxbybzb与 Ox(F)y(R)z(D)间的初始方位角和决定导航计算的目标坐标系.
2.1 初始方位角对位移计算的影响分析
SVP点胫骨与地面垂直,如图4(a)所示.将此时Oxbybzb对应位置所处的坐标系定义为 OXYZ.若IMU位置理想,行走路面与水平面平行,则OXYZ与Ox(F)y(R)z(D)完全重合,初始方位角均为零.一般情况下,IMU绑定位置存在差异,路面并不平整,行走过程中SVP点时OXYZ并不与Ox(F)y(R)z(D)重合,而是存在一定的初始方位角.图4(b)表示两坐标系间存在的方位角关系,绕 y(R)轴旋转的角度为俯仰角(Pitch),绕 x(F)轴旋转的角度为横滚角(Roll),绕z(D)轴旋转的角度为偏航角(Heading).图4(c)给出了两坐标系存在方位角ψ、ρ γ和 时的转换示意.
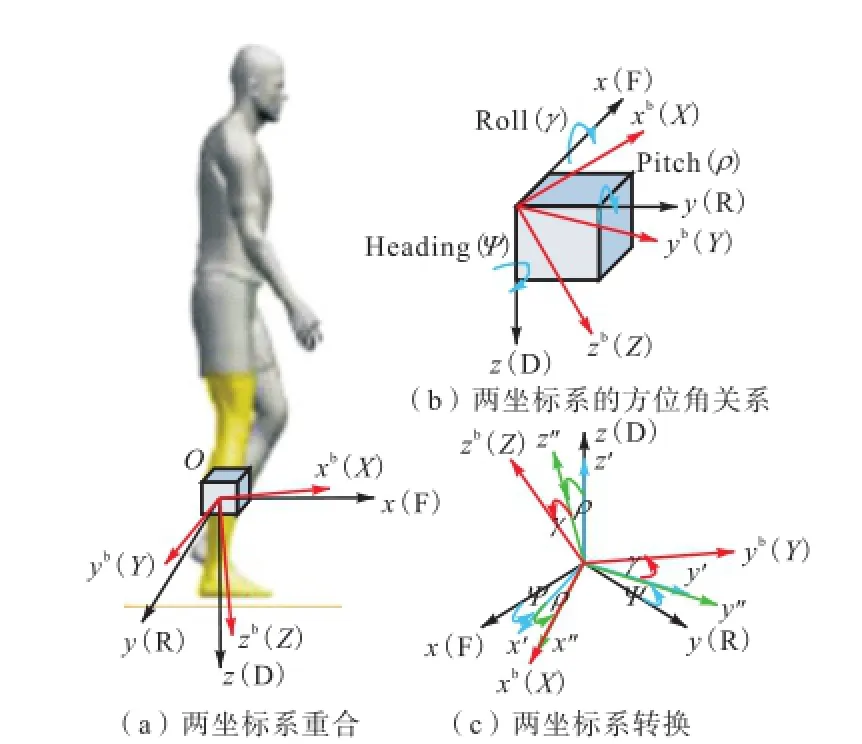
图4 SVP时刻机体坐标系位置Fig.4 Position of Oxbybzbat shank vertical point
Li等[12]认为行进过程中的胫骨运动符合倒立摆模型,利用该模型对式(2)描述的导航方程进行近似:①假设图 2中 t1和 t10时刻 IMU机体坐标系Oxbybzb对应位置与 Ox(F)y(R)z(D)完全重合,即和全为零;②假设行进过程中IMU所在胫骨部位只在Ox(F)z(D)平面运动,即ψ、γ为零.根据①和②近似可知,坐标系 OXYZ和 Ox(F)y(R)z(D)完全重合.OXYZ和Ox(F)y(R)z(D)坐标系下的导航方程为
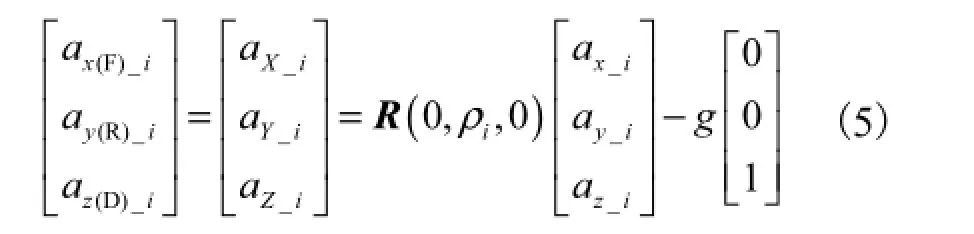
该近似方法在平整的地面或跑步机上测试,能达到较高的计算精度且所需计算量小,惯性数据采集只需二轴加速度计和单轴陀螺仪.但这种简单的初始方位角假设同时又忽略行进过程的三维特性,对IMU绑定位置和人员行走方式的要求十分苛刻,测试系统操作复杂,局限性大.
每一步SVP点时,OXYZ相对于Ox(F)y(R)z(D)的方位角为和重力加速度方向指向地心,与z(D)方向相同,因此重力加速度g只在z(D)轴上有分量.根据 OXYZ与 Ox(F)y(R)z(D)间的转换关系,可得重力加速度在 OXYZ坐标系下三轴分量为
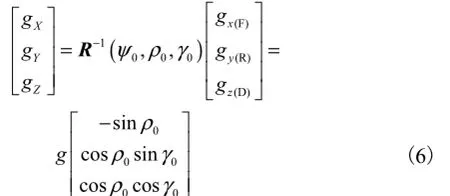
文献[12]将不为零的初始方位角假设为零值,在此基础上通过角速度去更新坐标系转换关系,等同于将1步内所有时刻的加速度值映射到OXYZ坐标系,在该坐标系内计算位移.但重力加速度的去除却是按照 Ox(F)y(R)z(D)坐标系下的处理方式进行.该方法在重力加速度去除过程中存在的误差为
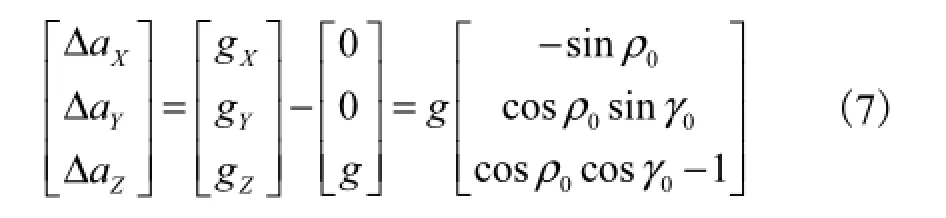
由图 2中可看出测试人员行走 1步持续时间 t1到 t10大约为 1,s.若取和均为 5°,重力加速度为 9.8,m/s2,则式(7)描述的加速度误差在 O,XYZ坐标系内计算的位移误差为:该误差足以导致错误的步长计算,可见初始方位角对重力加速度去除的影响不可忽略.
2.2 初始方位角为参量的步长计算方法
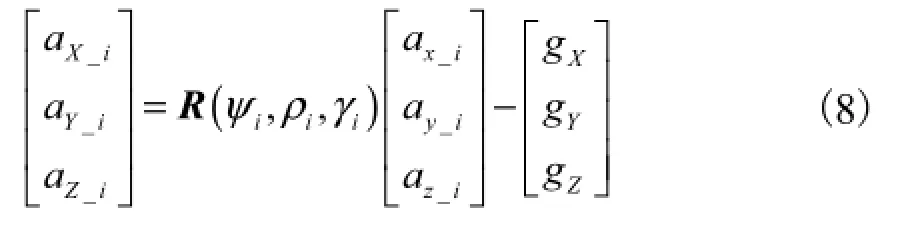
联立式(6)和式(8),结合惯性导航原理可计算出行走 1步在 OXYZ坐标系下产生的三轴位移矢量和将 OXYZ下的位移投影到定位目标坐标系Ox(F)y(R)z(D)内,有
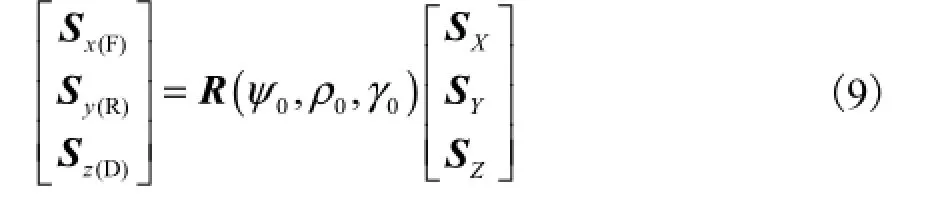
计算得到坐标系OXYZ和Ox(F)y(R)z(D)下的位移均为初始方位角和的函数表达式.Ox(F)y(R)z(D)是以人员行走方向 x(F)为基准建立的本地坐标系,由 OXYZ坐标系的定义可知,两坐标系间的方位角(偏航角)0ψ为零.
由第1.1节可知,在每个SVP点,人体需克服重力使胫骨与地面垂直来实现身体平衡.可认为在坡度较小(小于 20°)的路面上,胫骨垂直于地面,即图4(a)中OYZ和Oy(R)z(D)在同一平面内,0γ为零.
结合式(6)和式(8),OXYZ坐标系下的导航方程简化为
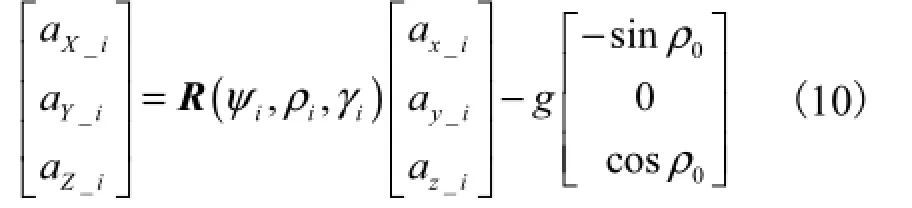
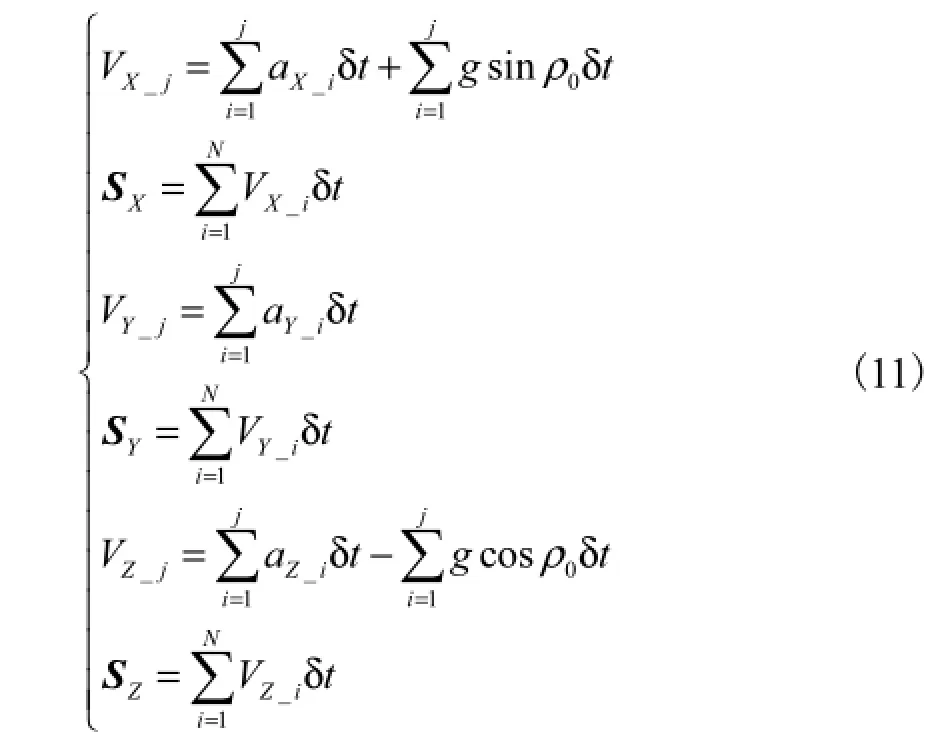
式中N为1步内采样得到的惯性参量个数.
由OXYZ坐标系的位置定义可知,X轴位移分量SX为人员沿着路面向前的位移,Y轴位移分量 SY为人员沿着路面右向的位移.X轴和Y轴位移分量的矢量和即为步长.因此,步长Step_Length的计算式为
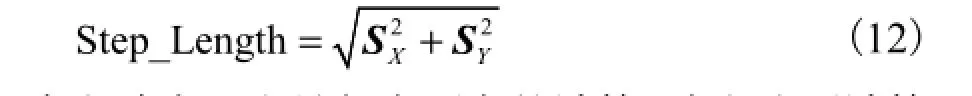
本文致力于人员行走距离的计算,式(12)可计算出每1步的步长,累加所有步长即得行走距离.
2.3 初始方位角的解算
通过大量的测量实验,人的行走步长一般不超过1.6,m(1步包括左脚和右脚均向前迈进 1步).对于坡度较小的道路,可认为1.6,m内的路面在一个平面上且Z轴指向垂直于地面方向.因此在1步内,垂直地面方向的位移为零,即结合式(11),有
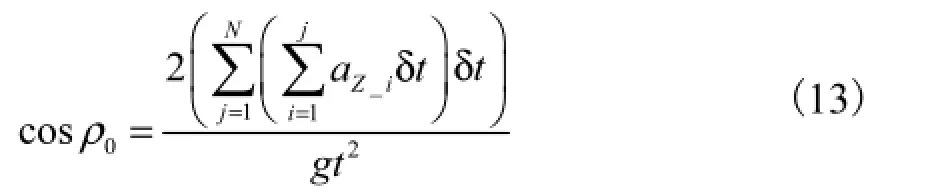
由三角函数关系式,有
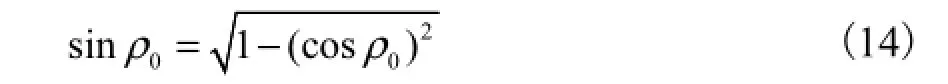
将式(14)代入式(11)中XS的表达式计算出XS的数值,结合式(11)中已经计算出具体数值的YS,据式(12)得到行进步长.
3 系统实现及实验结果分析
3.1 实验系统搭建
战略柔性是企业技术创新的源泉,是企业高效利用资源的重要保障。通过增强战略柔性,提高资源柔性和协调柔性水平,增强中小企业自主创新能力,提高生产效率,先于竞争对手进入新市场。
惯性测量单元 IMU选用模拟器件公司 ADI生产的ADIS16405,BMLZ,如图5所示.该惯性模块集成测量范围可伸缩设置的三轴陀螺仪、三轴加速度计、三轴磁力计和内置的温度传感器.内部元件正交坐标轴与封装机体坐标轴的对准角度偏差小于0.05°,噪声密度小于 0.05°·s-1在设定的内部采样周期下,IMU对其运动惯性参量进行采样并更新对应的内部寄存器值,其最高采样率可达 819.2次/s,并提供标准串行外设接口(serial peripheral interface,SPI).外部处理单元可通过 SPI接口直接访问其内部寄存器,读取惯性参量.

图5 实验系统采用的惯性测量单元Fig.5 Inertial measurement unit for experimental system
外部处理单元主要由便携式计算机组成,利用Cypress公司 CY7C68013A-128AXC桥接计算机和IMU器件.计算机通过USB接口将IMU采样的惯性参量读取到内存,进行实时分析和计算,并保存原始惯性数据.本文设定IMU的采样频率为409.6次/s.
实验中,便携式计算机选择联想 Thinkpad X220,其配置为:CPU i5-2520,2.5,GHz,内存DDR3 4,GB.操作系统为Windows XP Professional SP3,计算软件环境为Matlab 2008a.
3.2 实验人员及实验描述
实验人员为课题组中志愿进行行走测试的 3名学生,身高分别为168,cm、171,cm和175,cm.
行走路面选择室外长为103.5,m的普通道路.每个测试人员均按平常的走路习惯,分别以正常速度、快速、慢速和快慢速无规律交替的变速 4种行走速度,在该段路面进行来回行走实验.要求每个测试人员每个速度等级均有一次来回实验.每名测试者至少有 7次实验数据,其中每个实验至少进行了 4次.3名测试人员按上述方法共测得34组数据,每组数据按测试人员和行走速度等级分别标记.
3.3 实验结果分析
为了验证本文提出的基于改进步长估计的行走距离计算方法的准确性,利用Matlab对34次行走实验保存的惯性数据进行离线分析与计算.
计算步长前,先对连续行走过程进行分步处理使惯性数据与行走过程每个阶段相互对应.第1.1节中对行走过程进行了详细的分解,胫骨与地面垂直时,三轴角速度几乎为零.行走过程中,胫骨沿yb轴做类似倒立摆运动,其角速度信号较为明显,通过 yb轴角速度找出每一步 SVP点.选取其中一位测试人员在正常行走速度下测得的惯性数据为例,标出选定的SVP点,如图6所示的红色圆点.图6中,xb和zb轴的角速度信号在 SVP点也几乎为零,进一步印证了SVP点可作为ZUPT点.
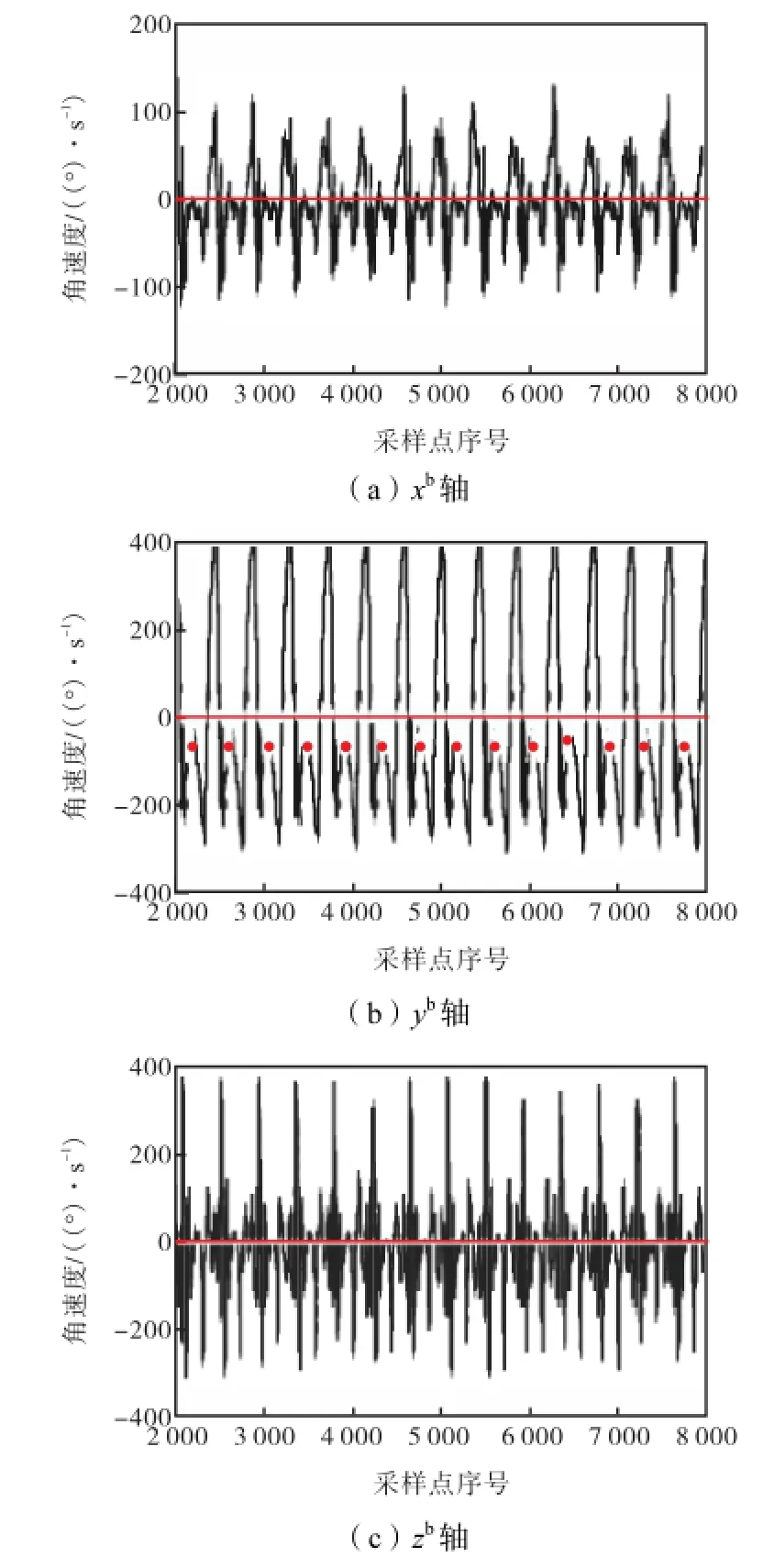
图6 行走过程角速度数据及ZUPT点分步Fig.6 Angular velocity of walking and ZUPT points
利用第 2节所述的胫骨捷联惯性位移导航计算方法,以每一步为导航周期计算步长,累加所有步长得到每次实验所行走的距离,用Proposed_Method标记.同时,按照文献[12]所运用的方法计算每一步的步长和总的行走距离,标记为 Ref_Method.文献[12]只考虑了人员行走过程的二维运动,忽略其三维特性.本文在其基础上考虑了运动的三维特性,将单轴角速度改为三轴角速度来计算转换矩阵,实现三轴加速度的分解,其他计算方法和步骤与之完全相同,计算步长和总的行走距离,标记为3DMotion_Method.
分别将3种方法计算的总距离与实际行走的距离103.5,m进行比较,得到34次实验3种算法距离误差的百分比曲线,如图7所示,横轴表示实验次数,纵轴表示该次实验行走距离误差百分数.对比34组实验结果,并按其误差范围进行相应的统计,如表1所示,得出行走距离误差在一定范围内的概率分布情况.
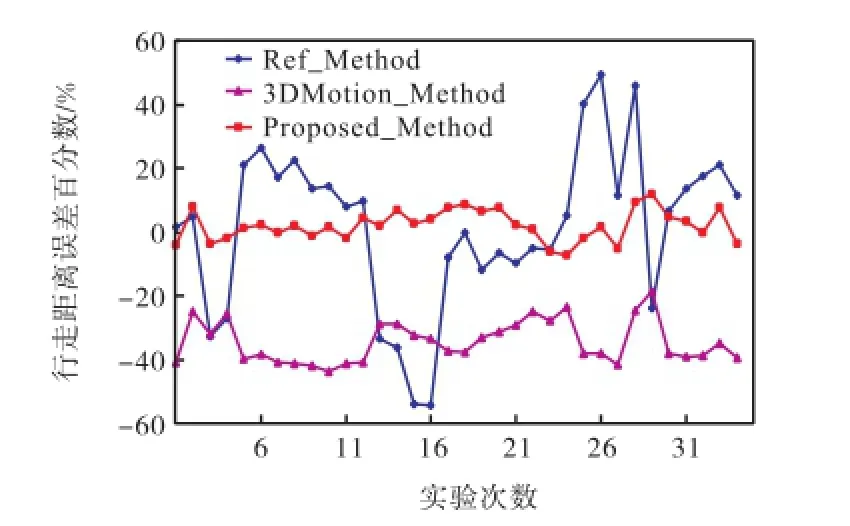
图7 3种算法下行走距离的误差比较Fig.7 Comparison of the distance error for three methods
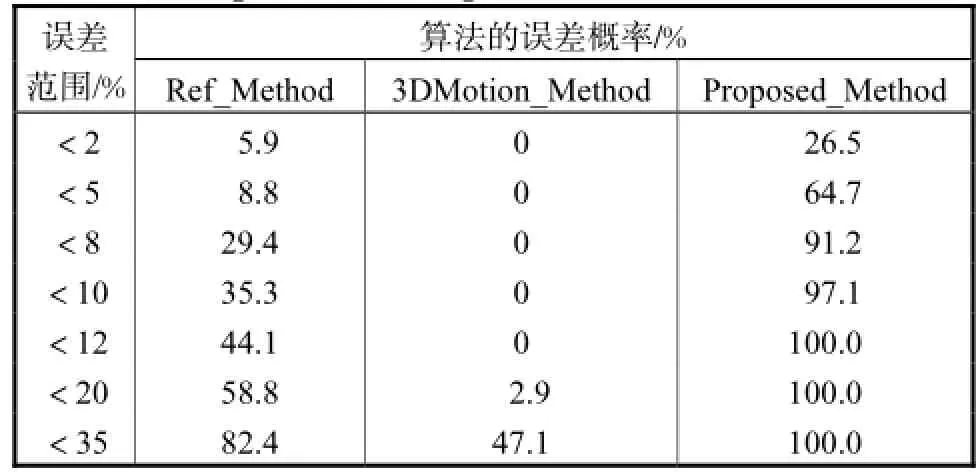
表1 3种算法性能比较Tab.1 Comparison of the performance for three methods
由图7可知,只考虑二维运动且设定初始方位角为零的 Ref_Method方法,每次实验计算的总距离与实际行走距离间的误差较大,每次实验误差的波动范围也较大.导致此类误差的主要原因是:①对不同的测试人员,IMU的绑定位置并不能完全满足该算法的要求,使得在 SVP点,初始方位角与零值相差较大,按零值处理产生较大的位移偏差;②在不平整的道路上,走路姿势随意,使胫骨运动不是理想的二维模型,从而导致重力加速度的分解并不完全在一个二维平面内.导航方程中水平和垂直两方向的加速度并不完全由人员行走运动产生,而是叠加了重力加速度去除过程产生的误差.
相比Ref_Method方法,3DMotion_Method方法充分考虑了行走的三维特性.但初始方位角设定为零,导致在 SVP点时分解重力加速度产生与Ref_Method方法相同的去除误差.初始方位角为零还使得 3DMotion_Method没有去除重力加速度在水平方向的分量,而是与线性加速度叠加.水平方向的线性加速度比实际加速度小,计算的步长普遍偏小,总距离误差较大.相对 Ref_Method,3DMotion_ Method误差波动范围较平缓,说明考虑运动的三维特性能减小步长计算的差异程度.
Proposed_Method在 3DMotion_Method的基础上,假设初始方位角未知,并不直接将其设定为零值.导航计算出含有未知数的位移表达式,从而使重力加速度的去除过程无任何近似.方位角的解算和步长的计算过程,可看成由垂直地面方向位移ZS的误差,得到水平位移的补偿参量0sinρ,用来修正水平方向的位移XS和YS,使水平位移更准确,提高步长计算的精度.实验结果表明,Proposed_Method的位移误差较 3DMotion_Method和 Ref_Method小得多.因此,三维运动特性和初始方位角均对步长计算的精度有较大影响,应充分考虑这两者在基于捷联惯性导航的人员位置跟踪算法中的处理方法.本文提出的方位角解算步长改进算法提高了步长计算的精度和稳定性,将误差控制在行走距离的10%以内.
结合图7,表1显示Proposed_Method距离误差范围小的概率较 3DMotion_Method和 Ref_Method有较大幅度提高. 3DMotion_Method相比Ref_Method小误差范围的概率小,大部分为零;但其误差曲线相对较平缓,得益于三维运动特性下的加速度转换.Proposed_Method在3DMotion_Method基础上,加入初始方位角解算,性能大幅度提升,计算的行走距离误差在8%以内的概率为91%.
图 8对 4种行走速度等级下距离计算误差进行了对比.由图8可见,Proposed_Method和3DMotion_ Method在各种速率等级下误差相对平缓,Ref_Method误差波动大,无规律.说明行走速度对运动的三维特性有较大的影响.Proposed_Method在3DMotion_Method的基础上进行初始方位角解算,误差减小.说明行走速度对 SVP点初始方位角的影响不可忽视.Proposed_Method能很好地适应各种行走速度,适用性较好.
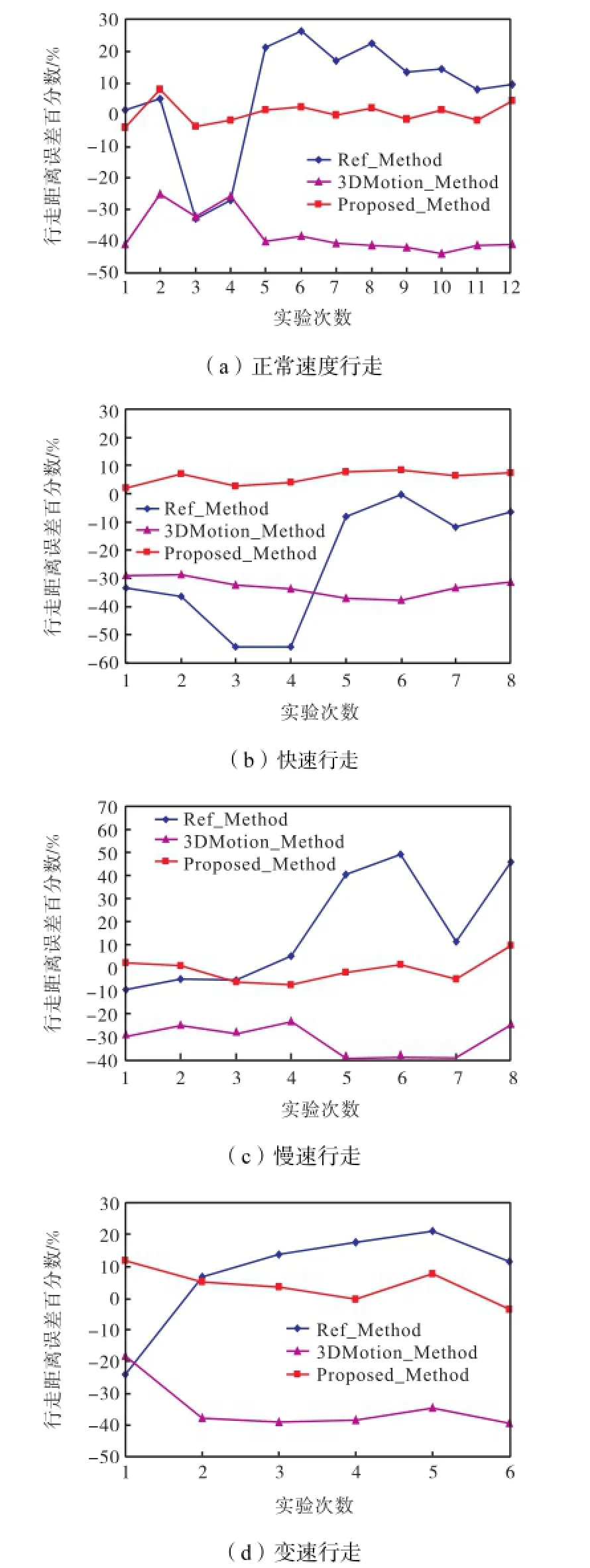
图8 不同行走速度下的距离误差比较Fig.8 Comparison of the distance error for different walking speeds
图9对比了3位测试人员的行走实验结果.由于测试人员1的实验次数较多,故将测试人员2和3的实验数据放在一起.图 9(a)为测试人员 1的行走实验结果;图9(b)为测试人员2和3的实验结果,其中前 7次为测试人员 2,后 6次为测试人员 3.由图 9的实验结果可知,每位测试人员距离计算误差Proposed_Method较3DMotion_Method和 Ref_ Method均小得多.Proposed_Method对人员的适应性较好,不同的行走人员无需更改任何系统参数,通用性较好.
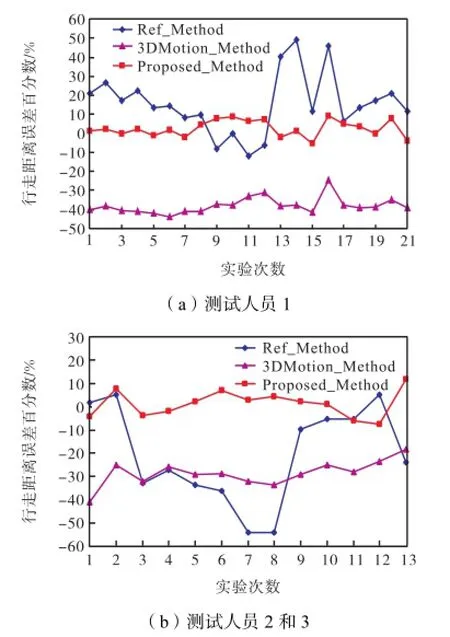
图9 不同测试者的行走距离误差比较Fig.9 Comparison of the distance error for differenet volunteers
4 结 语
本文改进了步长计算过程中 ZUPT时刻捷联惯性导航初始方位角参数的设定方法,以该方位角为中间量推导步长的函数关系式.详细分析人员行走时胫骨运动特性和初始方位角的特点,提出三轴位移的近似方法和约束条件,解算初始方位角并求得步长,进而估计人员行进距离.该方法将重力加速度的去除误差从重积分中剥离出来,避免了重积分对误差的扩散,提高了步长计算的精度.且该方法对人员行走方式无特殊要求,对不平整路面的适应性也较好.通过 34次 103.5,m的不平整道路上直线行走实验验证,计算的行走距离误差在8%以内的概率为91%.
本文基于惯性导航原理对人员行进的距离进行估计,为室内人员定位跟踪提供一种可参考的相对位置估计方法.但惯性导航固有的累积误差无法满足长时间的室内人员定位需求.未来的研究中,将会加入一定精度的绝对定位方法,与精度相对较高的短时惯性导航定位结合,实现高精度的室内人员定位跟踪及导航系统.
[1] Jimenez A R,Seco F,Prieto C,et al. A comparison of pedestrian dead-reckoning algorithms using a low-cost MEMS IMU[C]// Intelligent Signal Processing(WISP). Budapest,Hungary,2009:37-42.
[2] Torres-Solis J,Falk T H,Chau T. A Review of Indoor Localization Technologies:Towards Navigational Assistance for Topographical Disorientation[M]. Rijeka,Croatia:Ambient Intelligence,2010:51-83.
[3] Woodman O. An Introduction to Inertial Navigation[R]. Cambridge,UK:University of Cambridge,2007.
[4] Kelly A. Personal Navigation System Based on Dual Shoe-Mounted IMUs and Intershoe Ranging[R]. MA,USA:Precision Personnel Locator Workshop,2011.
[5] Mathiassen K,Hanssen L,Hallingstad O. A low cost navigation unit for positioning of personnel after loss of GPS position[C]// International Conference on Indoor Positioning and Indoor Navigation(IPIN). Zurich,Switzerland,2010.
[6] Abdulrahim K,Hide C,Moore T,et al. Aiding MEMS IMU with building heading for indoor pedestrian navigation[C]// Ubiquitous Positioning Indoor Navigation and Location Based Service(UPINLBS). Helsinki,
Finland,2010:1-6.
[7] Castaneda N,Lamy-Perbal S. An improved shoemounted inertial navigation system[C]// International Conference on Indoor Positioning and Indoor Navigation(IPIN). Zurich,Switzerland,2010.
[8] Jimenez A R. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a footmounted IMU[C]// 7th Workshop on Positioning Navigation and Communication(WPNC). Germany,2010:135-143.
[9] Nilsson J O,Skog I,El P. Performance characterization of foot-mounted ZUPT-aided INSs and other related systems[C]// International Conference on Indoor Positioning and Indoor Navigation(IPIN). Zurich,Switzerland,2010.
[10] Huang C,Liao Z,Zhao L. Synergism of INS and PDR in self-contained pedestrian tracking with a miniature sensor module[J]. IEEE Sensors Journal,2010,10(8):1349-1359.
[11] Alvarez D,Gonzalez R C,Lopez A,et al. Comparison of step length estimators from wearable accelerometer devices[C]// 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. USA,2006:5964-5967.
[12] Li Q,Young M,Naing V,et al. Walking speed estimation using a shank-mounted inertial measurement unit[J]. Journal of Biomechanics,2010,43(8):1640-1643.
(责任编辑:金顺爱)
Pedestrian Walking Distance Estimation Based on Strap-Down Inertial Navigation of Shank
Wang Shaochu1,2,Liu Kaihua1,Liu Yu1
(1. School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Institute of Surveying and Mapping,Tianjin 300381,China)
This paper studies the step length calculation scheme based on shank mounted inertial measurement unit (IMU), and proposes a method for initial parameters resetting at the zero velocity update (ZUPT) time of one navigation period. The accurate expressions of three-dimensional displacement functions based on initial orientationwere obtained without diffusion of approximation error by double integral. Taking into account the pedestrian walkingcharacteristics and the vertical relationship between the shank and pavement at the moment of ZUPT, with the restraint of vertical displacement being regarded as zero at one navigation period, the other two horizontal displacementswere calculated, and the step length was easily obtained. Without modifying the parameters of the system, this method has the advantages of adaptability and versatility for different pedestrians and walking environments. By volunteers’ walking experiment verification, the probability of total walking distance error less than 8% is 91%.
strap-down inertial navigation;zero velocity update;pedestrian dead-reckoning
TN967.2
A
0493-2137(2014)08-0719-09
10.11784/tdxbz201211045
2012-11-23;
2013-01-07.
国家自然科学基金资助项目(61373102).
汪少初(1983— ),男,博士研究生,wangshaochu@tju.edu.cn.
刘开华,liukaihua@tju.edu.cn.
