基于严格耦合波理论的新型耦合光栅分析

尤 勐，黄战华，蔡怀宇

基于严格耦合波理论的新型耦合光栅分析

尤 勐1,2，黄战华1,2，蔡怀宇1,2

(1. 天津大学精密仪器与光电子工程学院，天津 300072；2. 天津大学光电信息技术教育部重点实验室，天津 300072)

针对波导全息平视器中一种新型的耦合光栅结构，基于严格耦合波理论数值分析了其衍射特性，同时对光栅的工艺容差进行了分析，计算了膜厚、槽深、周期与入射波长对耦合效率的影响．该光栅以波导板中内嵌的闪耀光栅锯齿面作基底，镀高折射率的膜层后，覆盖锯齿状的金属膜层．计算结果表明：对于波长532,nm的TE偏振光，空气中0°入射的一级衍射效率可大于90%；当空气中入射光的纵向角在[-8°，12°]、横向角在[-15°，15°]内变化时，一级衍射效率可大于82%且保持平稳．该光栅可在波导全息平视器中，对大视场成像光束进行均匀、高效的耦合．

光栅；衍射效率；严格耦合波理论

波导型全息平视显示器件(waveguide holographic helmet mounted display，W-HMD)是由英国军火商BAE Systems公司推向市场的一种新型屏显器件[1]，其功能在于同时显示外界目标与舱内参数，减轻驾驶员的操作负担．相较于传统的反射式屏显，该设计采用波导折叠光路的方式，可压缩空间结构，使其更加小型集成化．但是该器件要求各视场的成像光束均匀、高效地耦合入波导板内，以完成对出瞳的二维展开．前人在光栅耦合领域做了许多工作，但很少考虑宽角度入射下光栅的耦合特性[2-4]．2010年BAE Systems公司在相关专利中公布了一种新型的耦合光栅结构[5]，可以很好地解决宽角度、大视场入射下光束的耦合问题，并将其应用到W-HMD的工业生产中．但是限于专利的保密性，该光栅的组成材料、结构细节、衍射特性等参数并未得到披露，且鲜有文献做过详细的报道．

笔者基于严格耦合波理论(rigorous coupled wave analysis，RCWA)，选取了特定的光栅材料，数值分析了宽角度入射下该新型光栅的衍射效率．同时，对光栅的工艺容差进行了分析，计算了膜厚、槽深、周期与入射波长对耦合效率的影响，可对光栅的实际制作加工提供理论指导．

1 RCWA的计算简述

由于耦合光栅的特征尺寸在波长量级，本文选择了RCWA进行矢量计算，以求得各级衍射效率的严格解．RCWA的出发点在于各层相应级次的横向谐波耦合，即空间频率需要保持一致．以TE波入射为例，先求出入射与透射区域的电场表达式EⅠ,y和，即

再由Maxwell方程得到光栅内部的电磁场分量Egy和Hgx，即

结合光栅内的介电常数()xε′并在0z=和zd=处运用边界条件，得到不同介质分界面电磁场的连续分量，列方程组即可求解各衍射级次的能量．求解过程中采用透射矩阵以提高计算效率，并运用薄层光栅的递推方法以避免数值的不稳定．

编程后，以北京大学Fu等[8]所述的参数进行设定，计算矩形金属光栅的衍射效率．图1为该光栅在不同占空比的条件下，反射率与刻槽深度的关系曲线，与文献[8]相符，可证明程序编写正确．

图1 矩形金属光栅的衍射效率Fig.1 Diffraction efficiency for square-wave metal grating with different filling factors

2 新型耦合光栅的衍射特性

2.1 光栅结构

如图2(a)所示，该光栅由3部分组成：第一部分是下基底，与波导板相黏合，上端呈锯齿状，选用二氧化硅(SiO2)，折射率为1.52；第二部分是在锯齿斜面镀的膜层，选用二氧化钛(TiO2)，其折射率为2.5；第三部分是上基底，由金属银(Ag)组成[9-10]．设图2(a)中光栅的周期为T，闪耀槽深为d，膜层的厚度为x．

在RCWA程序中模拟该光栅的一个周期，设定分层数目为50，如图2(b)所示．图中白色区域表示下基底，灰色区域表示上基底，黑色区域表示膜层．编写相应代码后代入RCWA程序计算各级衍射效率．

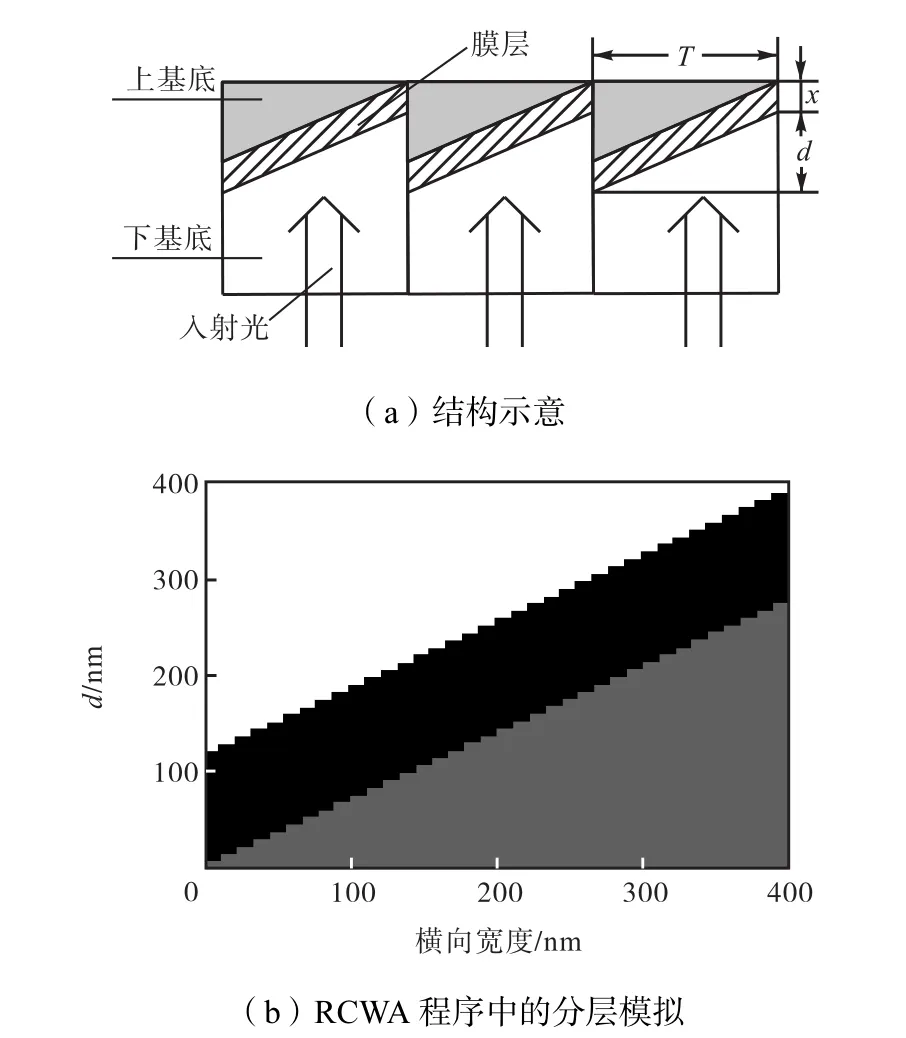
图2 新型耦合光栅结构Fig.2 Structure of the novel coupling grating

2.2 0°入射下的衍射效率

由于光栅结构中存在金属介质，经过程序的多次尝试性计算后，选择入射光为TE模偏振，可以获得较好的衍射特性．考虑人眼对波长的灵敏度以及常用图像源的波长范围，选择入射波长为532,nm．考虑常用的波导介质，选择折射率为1.52．光束耦合入波导后，会以全反射的方式在波导内部传播，如图3所示．

由于W-HMD视场内的光束均需满足波导内的全反射条件，根据波导1.52的折射率计算，全反射角度至少大于42°．同时为了满足光束在波导内存在足够的反射次数，全反射角度不宜大于75°．所以在[42°，75°]的角度范围内，选择60°作为视场中心光束(即图3中纵向角b=0°的光束)在波导内的全反射角度，以满足大视场光束的耦合需求．因此可计算得到光栅的周期T=410,nm．此时光束以纵向角b= 0°入射，正一级衍射光将在导板中全反射传播，与底面夹角约60°，如图3所示．

图3 耦合光栅与波导板示意Fig.3 Combination of coupling grating and the waveguide

为了比较新型耦合光栅的性能，图4(a)给出了普通锯齿光栅的衍射特性(即图2(a)中去除膜层，上、下基底直接黏合)．其中(0)R、(-1)R、(+1)R分别代表零级、负一级、正一级的衍射．在槽深d增加至250,nm时，普通锯齿光栅的正一级衍射效率为60%，负一级衍射效率接近20%．

图4 RCWA计算的各级衍射效率Fig.4 Diffraction efficiency changing with parameters calculated by RCWA

图4 (b)给出了新型耦合光栅随膜厚x变化的衍射效率．经过程序的多次计算，设定槽深d= 240,nm，此时膜厚x变化时，光栅可以获得衍射效率的峰值．可以看出，当x在[50,nm，150,nm]范围内变化时，正一级衍射效率接近90%，零级与负一级均低于5%．随着x的继续增加，正一级衍射效率递减而零级效率递增，同时在x=180,nm、380,nm、450,nm处，存在明显的导模共振现象．为了获取较高的耦合效率，本文选择膜厚x=96,nm，此时的正一级衍射效率可达90%．

2.3 宽角度入射下的衍射效率

当入射角发生变化时，导板内的正一级衍射角也会发生变化．为了满足全反射条件，设定入射纵向角b∈[-8°，12°]，横向角a[∈-15°，15°]，该角度范围可同时满足W-HMD 20°×30°的视场要求[11]．

设定d=240,nm，x=96,nm．图5(a)为a或b独立变化时，新型耦合光栅的正一级衍射效率曲线．图中两短虚线的间隔表示[-8°，12°]，长虚线表示随b变化的曲线，实线表示随a变化的曲线．可以看出，当b在[-8°，12°]或a在[-15°，15°]范围内变化时，一级衍射效率大于82%且变化平稳．

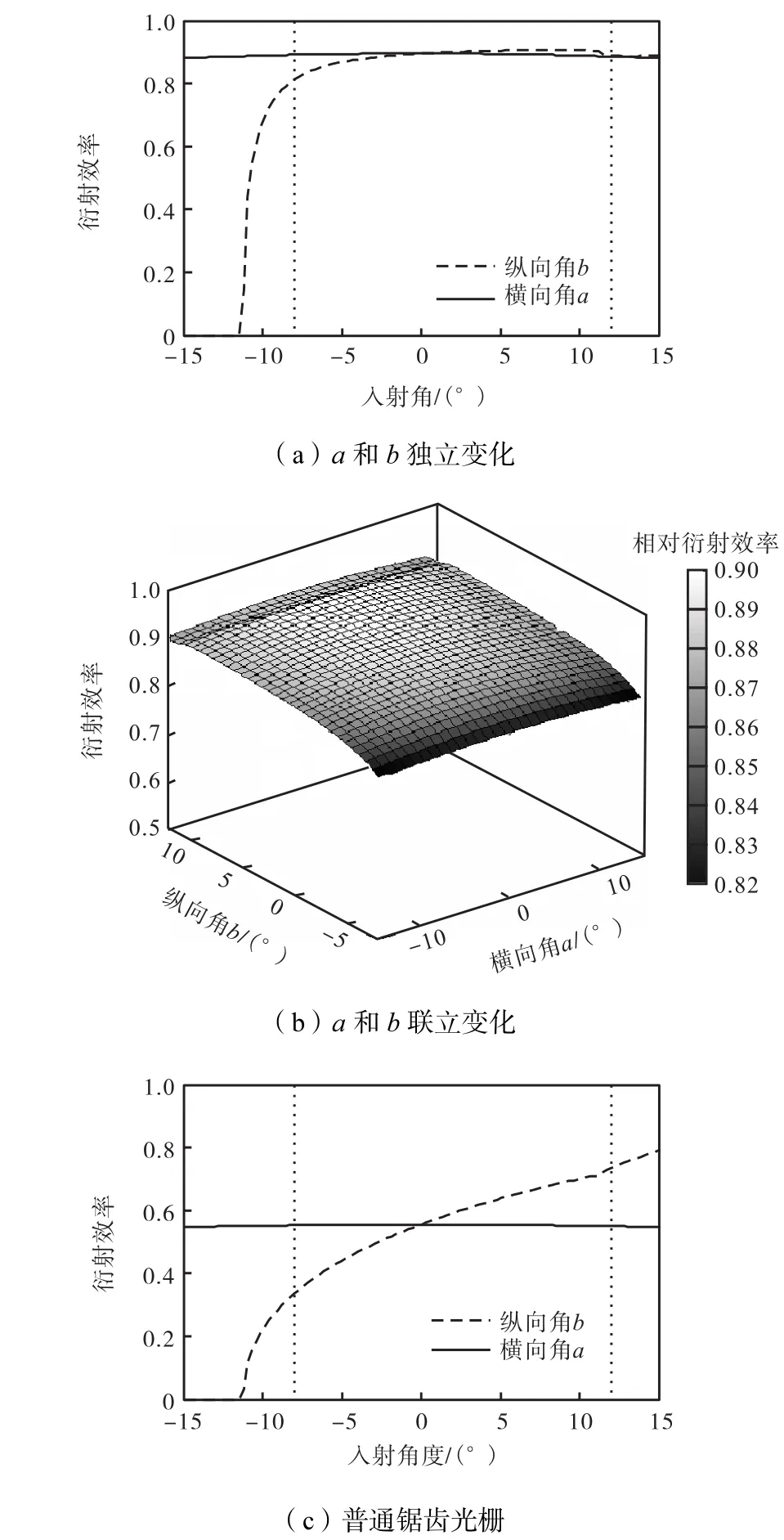
图5 随入射角度变化的衍射效率Fig.5Variation of diffraction efficiency with incident angle

在图5(b)中设定a和b联立变化，以模拟空间中任意角度入射的光束．可以看出，新型耦合光栅的正一级衍射效率依然大于82%，且几乎不随入射角而变．这种对角度的不敏感性，可使W-HMD中各视场的入射光均匀、高效地耦合入波导中．

作为对比，图5(c)显示了普通锯齿光栅的衍射效率曲线，很明显随b的变化幅度较大．

3 工艺容差分析

新型耦合光栅的制备需要离子束刻蚀、电子束蒸发等工艺[12-13]，在制备的过程中由于仪器精度或者加工流程等因素，使得成品与原先设计的参数相比，可能存在以下几方面的偏差：镀膜厚度x的偏差、槽深d的偏差、光栅周期T的偏差，同时入射光的波长也易在小范围内发生改变．本节讨论这些参数的变化对耦合效率的影响．

3.1 镀膜厚度x的偏差

在第2.2节已经讨论过膜厚与衍射效率的关系，由图4(b)可以看出，当膜厚在[50,nm，150,nm]范围内变化时，正一级的衍射效率均接近90%，在此范围外则迅速下降．

3.2 槽深d的偏差

图6(a)为槽深d在[0,nm，500,nm]范围内变化时，衍射效率的变化曲线．该曲线在d=234,nm达到峰值的90%，而后向两侧递减．当d[200∈,nm，280,nm]时，正一级衍射效率可大于85%；当d∈[180,nm，312,nm]时，正一级衍射效率可大于80%.

3.3 光栅周期T的偏差

当改变光栅的周期T时，正一级衍射光束与底面的夹角也会发生改变．为了满足全反射条件，同时观察图6(b)中随周期T变化的衍射效率，设定T[380∈,nm，500,nm]．在此范围内，衍射光束与底面的夹角在[45°，66°]之间，满足全反射条件且正一级衍射效率大于80%．

3.4 入射波长的偏差

在[400,nm，700,nm]内改变入射波长，同时改变银(Ag)随波长变化的折射率，计算所得的效率曲线如图6(c)所示．在考虑全反射条件后，得出波长在[480,nm，580,nm]范围内变化时，正一级衍射光束效率可大于80%．

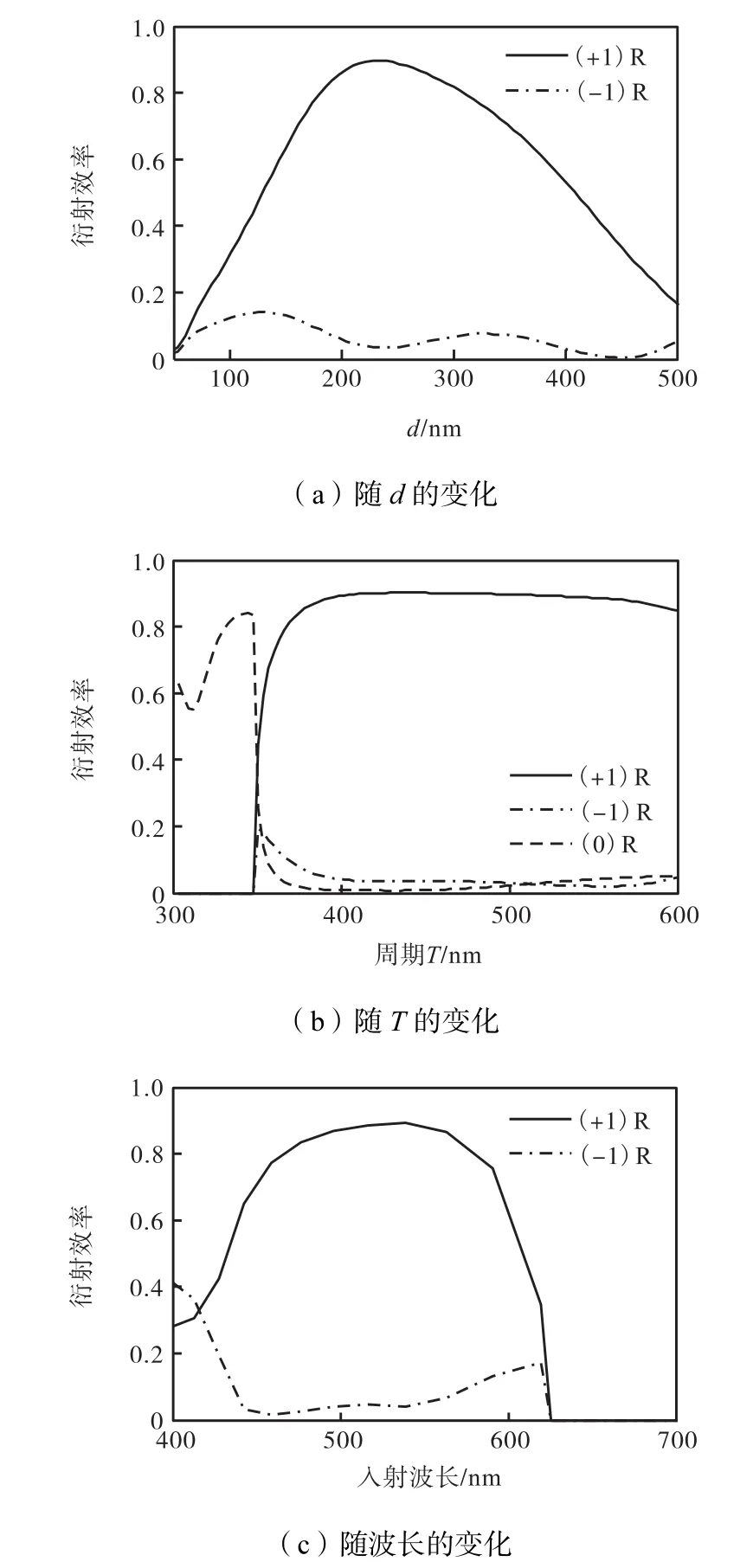
图6 工艺容差分析Fig.6Variation of diffraction efficiency with different parameters

4 结 语

本文对W-HMD中的新型耦合光栅进行了数值分析．在选取了光栅材料和入射条件后，光栅的正一级衍射效率在垂直入射下大于90%，宽角度入射下大于82%，且随入射角度的变化可保持平稳．该结构可在W-HMD中，完成大视场、高效率、均匀的成像光束耦合．最后对光栅的工艺容差进行了分析，为实际制作提供理论依据．

［1］ Simmons Michael，Howard Richard. A Projection Dis-play with a Rod-Like，Rectangular Cross-Section Waveguide and a Plate-Like Waveguide，Each of Them Having a Diffraction Grating：WO 2007/029034[P]. 2007-03-15.

［2］ Miller J M，Beaucoudrey N D，Chavel P，et al. Design and fabrication of binary slanted surface-relief gratings for a planar optical interconnection [J]. Applied Optics，1997，36(23)：5717-5726.

［3］ Wang B，Jiang J H，Nordin G P. Compact slanted grating couplers [J]. Optics Express，2004，12(15)：3313-3325.

［4］ Chen H Y，Yang K C. Design of a high-efficiency grating coupler based on a silicon nitride overlay for siliconon-insulator waveguides [J]. Applied Optics，2010，49(33)：6455-6461.

［5］ Simmons Michael David. Improvements in Optical Waveguides：WO 2010/122330 [P]. 2010-10-28.

［6］ Moharam M G. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings [J]. Journal of Optical Society of America A，1995，12(5)：1068-1076.

［7］ Moharam M G. Stable implementation of the rigorous coupled wave analysis for surface-relief gratings enhanced transmittance matrix approach [J]. Journal of Optical Society of America A，1995，12(5)：1077-1086.

［8］ Fu Zhengping，Lin Feng，Zhu Xing. Numerical study on the optical absorption of one dimension metallic gratings [J]. Acta Physics Sinica，2011，60(11)：114213-1-114213-6.

［9］ Ghosh G. Handbook of Thermo-Optic Coefficients of Optical Materials with Applications [M]. San Diego：Academic Press，1998.

［10］ Palik E P. Handbook of Optical Constants of Solids [M]. 1st ed. San Diego：Academic Press，1998.

［11］ Huang Q，Caulfield H J. Waveguide holography and its applications[J]. SPIE Proceedings，1991，1461：303-312.

［12］ 王 宁，魏朝阳，邵建达，等. 电子束自动扫描SiO2材料沉积速率控制实验研究[J]. 中国激光，2010，31(10)：2615-2619.

Wang Ning，Wei Chaoyang，Shao Jianda，et al. Experimentation of deposition rate control of SiO2by E-beam auto-sweeping [J]. Chinese Journal of Lasers，2010，31(10)：2615-2619(in Chinese).

［13］ 徐宗伟，房丰洲，张少婧，等. 基于聚焦离子束铣削的复杂微纳结构制备[J]. 天津大学学报，2009，42(1)：91-94.

Xu Zongwei，Fang Fengzhou，Zhang Shaojing，et al. Fabrication of complicated micronano structures using focused ion beam milling method [J]. Journal of Tianjin University，2009，42(1)：91-94(in Chinese).

(责任编辑：赵艳静)

Numerical Analysis of a Novel Coupling Grating Based on RCWA

You Meng1,2，Huang Zhanhua1,2，Cai Huaiyu1,2
(1. School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Opto-Electronics Information Technology of Ministry of Education，Tianjin University，Tianjin 300072，China)

A novel coupling grating could play an important part in the waveguide holographic helmet mounted display，but to our knowledge few documents reveal its diffraction features in detail. Based on rigorous coupled wave analysis，the diffraction features are numerically analyzed. Tolerance analyses are also made of film thickness，groove depth，cycles and incident wavelength. The grating base is like the blazing grating etched in the waveguide. On the tilt surface，the film with high refractive index is first coated and then the metal is coated on the film in succession. The results show that for the TE-polarized incident light of 532,nm，the 1storder diffraction efficiency is larger than 90% with perpendicular incidence. It could remain stable with the incident angle from the air changing between [-8°，12°] vertically and [-15°，15°] horizontally. The 1st diffraction efficiency could be larger than 82% and keep stable. The proposed coupling gratingcould couple the image rays from large view fields into the display device with high efficiency and uniformity.

grating；diffraction efficiency；rigorous coupled wave analysis

O436.1

A

0493-2137(2014)03-0262-05

10.11784/tdxbz201206061

2012-06-26；

2012-08-10.

尤 勐(1986— )，男，博士研究生，ymeng@tju.edu.cn.

黄战华，zhanhua@tju.edu.cn.