用于相含率测量的螺旋电磁传感器优化设计

赵 倩，徐 凯，尹武良

用于相含率测量的螺旋电磁传感器优化设计

赵 倩，徐 凯，尹武良

(天津大学电气与自动化工程学院，天津 300072)

通过激励线圈和检测线圈，电磁传感器可以对被测物内部的电磁特性进行测量．为此，提出了一种用于相含率测量的新型电磁传感器——螺旋电磁传感器，进一步采用场量提取法推算了180°和360°螺旋线圈的灵敏度矩阵，并基于灵敏度分析对这2种传感器结构进行了优化设计，得到了优化参数的选取范围和规律．改进的螺旋电磁传感器具有更均匀、更灵敏的特性．同时，硬件实验表明，螺旋电磁传感器检测的电学敏感指标能够很好地反映被测物场的相含率，通过传感器的互感相角相对变化率与相含率的相关曲线，可以验证螺旋电磁传感器在相含率测量中的可行性和准确性．

电磁检测；相含率；螺旋电磁传感器；灵敏度

在工业中，油水两相流有着广泛的应用．而相含率作为一个重要参数，其准确测量对于生产过程的计量、控制和运行可靠性具有重要意义．目前已有很多相含率测量方法[1]，常用的有γ射线法[2]、微波法[3]、电容法[4-5]、电导法[6-7]和热扩散法[8]等．每种方法都有其特点和适用范围，如γ射线法测量范围大、结果准确，但需要放射源；微波法在测量精度、运行稳定性方面有一定优势，但安装困难，造价较高；电容法测量精度高，适用于油为连续相的流体，但适用范围小，只有在低含水率时才能保证精度；电导法适用于水为连续相的情况；热扩散法简单可靠，比较适合低含油率测量．

由于电磁测量具有非接触、非侵入、检测迅速等优点，研究人员也研究了如何利用电磁传感器来测量油水两相流的相含率[9]．其中线圈的设计是一个关键问题，对于电磁传感器而言，一般情况下靠近线圈处的灵敏度较大，而远离线圈的地方灵敏度较小．所以基于电磁传感器的电磁层析成像(EMT)[10-13]系统的灵敏度具有不均匀性，管道中心的灵敏度远远低于管道周边靠近线圈处的灵敏度[14-16]，因而相含率的测量精度会受到流型影响．同时增加测量通道和传感器个数，也使基于EMT的相含率测量装置较复杂．

针对上述情况，笔者提出了基于灵敏度分析的螺旋电磁传感器的优化设计．螺旋电磁传感器结构非常简单，每个传感器只含有一对沿轴向螺旋方式分布的激励和检测线圈，用于油水两相流的相含率测量时将更加方便．文中分别对180°和360°传感器的灵敏度分布做了分析，研究了张角对螺旋电磁传感器的影响规律，最终给出了螺旋电磁传感器结构的优化结果．同时结合硬件实验对螺旋电磁传感器在相含率测量中的应用进行了初步的探析．

1 灵敏度计算方法

由于在电磁测量系统中，检测物体通常为导磁性和导电性物质，所以文中采用了磁导率灵敏度和电导率灵敏度的灵敏性和均匀性作为参数来对螺旋传感器进行优化处理．灵敏度矩阵通常定义为感应线圈上电压变化量与引起该变化的物场空间中某个像素上电磁参数变化之比[17]．

在电磁测量系统中，某点的测量信号[15]表达式为

式中F为该点处电场强度E和磁场强度H的函数．

对于静态的媒质分布，当被测物场内媒质的电导率σ 或者磁导率μ 发生变化时，会引起电场强度E和磁场强度H的变化，进而使检测值F发生变化．

按照灵敏度的定义可以假设

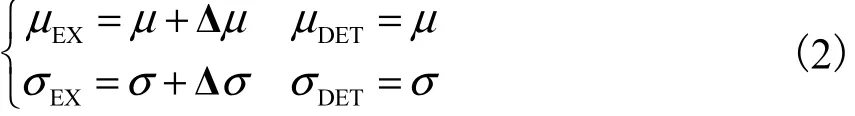
式中：符号Δ所引导的变量表示各物理量对应的变化量；下标EX和DET分别代表激励线圈和检测线圈．

它们产生的电场和磁场变化可以表述成类似形式为

式中：EEX、EDET和HEX、HDET分别为施加单位电流时，相互独立的激励线圈和检测线圈在被测区域形成的电场强度矢量和磁场强度矢量；下标EX0和DET0分别代表各场量的原始数值．

当系统激励信号为正弦信号时，根据麦克斯韦方程组可得

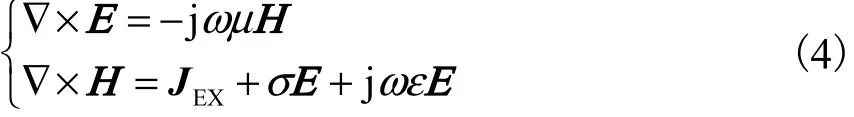
式中ω为电磁检测系统的工作频率．定义一个坡印亭向量SED=EEX×HDET，对其进行体积积分可得

式中：S为空间体V的正表面；n为指向曲面外侧的单位法向量．将式(2)～式(4)代入式(5)并结合矢量分析基本公式∇(a×b)=b·∇×a-a·∇×b，最终可得电磁测量系统对电导率和磁导率的灵敏度数学表达式[15,18]为

由式(6)可知，若已知系统和传感器结构，则可以分别求出激励线圈和检测线圈在场点处产生的电场和磁场，从而利用场量点乘法提取到相应的灵敏度图．

由于在管道流体的电磁检测中近似有E=jωA，所以可以通过AEX·ADET的方式计算电磁检测系统的电导率灵敏度矩阵．其中AEX、ADET分别为激励线圈和检测线圈在施加单位电流时的矢量磁位分布．

矢量磁位A的求解公式[19]为

同时，因为磁场强度H与磁感应强度B存在B=μH的关系，可以利用毕奥萨法尔定律[19]，即

来计算线圈激励下的磁感应强度B的分布，然后采用点乘的方法计算系统的磁导率灵敏度．

2 模型建立与结果分析

假定油水两相流物理模型参数如下：管道半径为100,mm，2种螺旋传感器高度都为400,mm．每个螺旋线圈对应的张角均记为θ．

以θ为变量，可以得到不同的灵敏度分布．为了使灵敏度图更全面反映传感器的性质，在这里采用八平面测量后求均值的方法求2种灵敏度．同时为了避免求平均值时的重复性，以xy平面为h=0,mm处，对360°线圈选择从h=25,mm到h=200,mm，每2个平面间距为25,mm；对于180°线圈，选择从h= 50,mm到h=400,mm，每2个平面间距为50,mm．图1为2种线圈的结构示意，其中线圈1为激励线圈，线圈2为接收线圈．

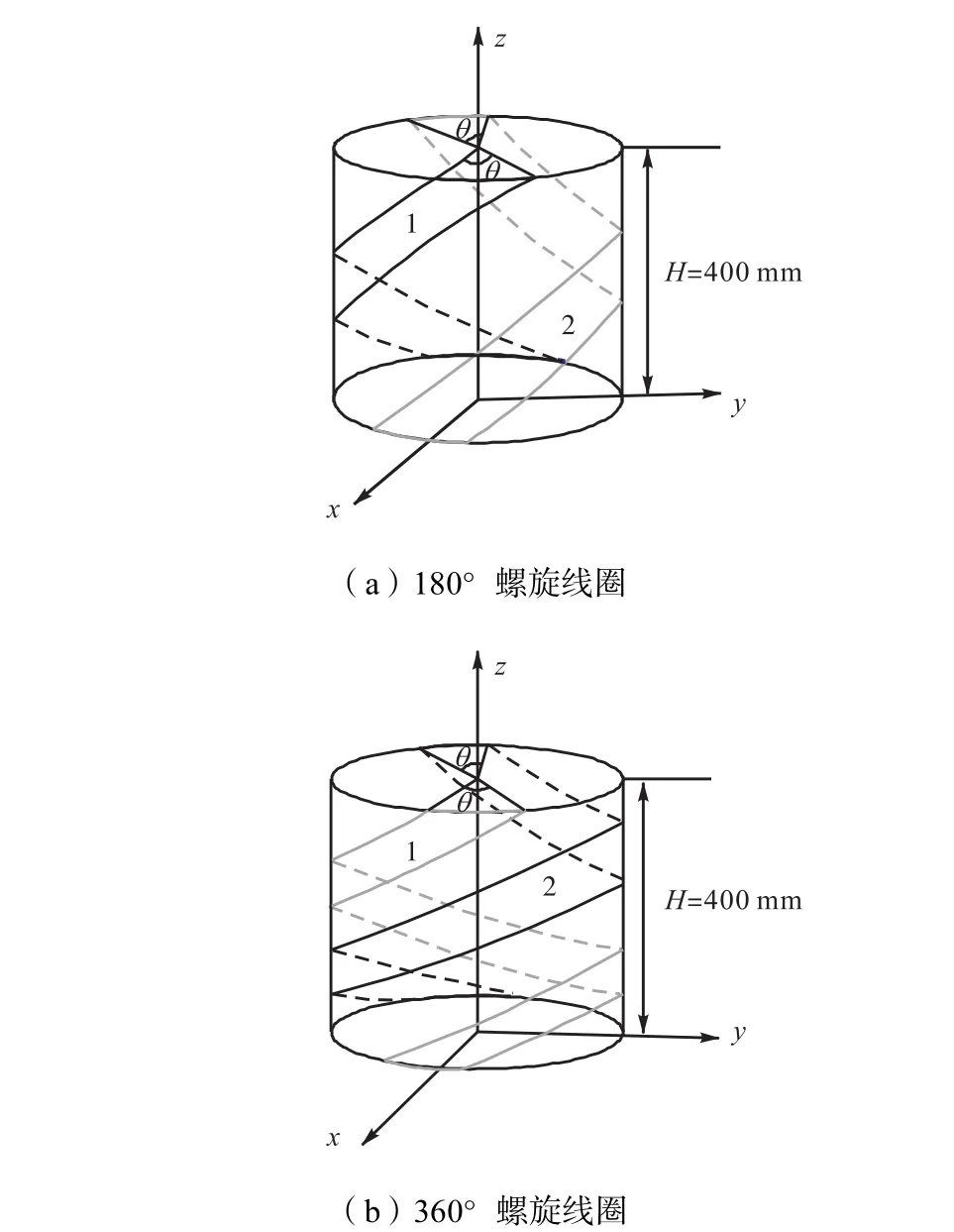
图1 两种螺旋线圈的结构示意Fig.1 Schematics of two spiral sensor structures

依据前面所讲的点乘法，当2种螺旋线圈的张角均为0.4,π时，电导率灵敏度和磁导率灵敏度如图2和图3所示．

为了定量分析不同张角所对应灵敏度场的优劣，这里定义了以下3个灵敏度的评价指标.

传感器平均灵敏度为

传感器灵敏度场标准差为

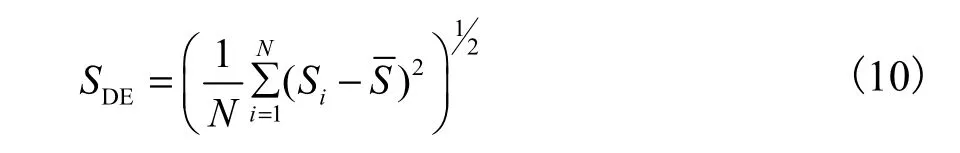
传感器灵敏度场相对标准差为

式中：Si为敏感场内第i个像素位置处的灵敏度值；N为敏感场内的像素总数．传感器平均灵敏度和相对标准差分别反映了该传感器的灵敏性和均匀性．而SRS越小，说明测量所受流型的影响越小，所以SRS是个关键参数．

当张角θ不同时，可以得到不同的灵敏度分布，采用该组评价指标对180°和360°螺旋传感器模型的灵敏度矩阵进行对比分析，如表1和表2所示．

用MATLAB画出2种螺旋线圈灵敏度均值和灵敏度相对标准差与张角的关系曲线如图4～图7所示.

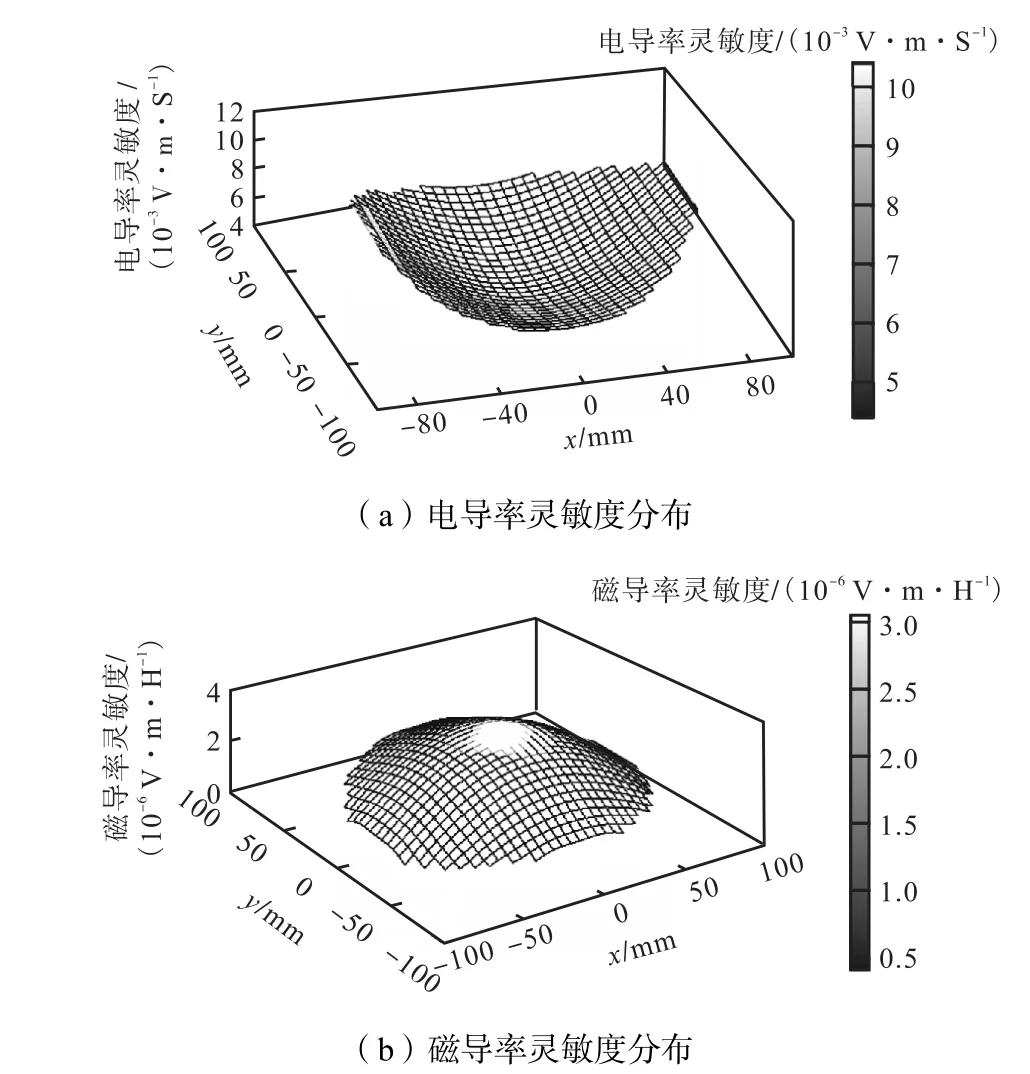
图2 180° 螺旋传感器灵敏度分布Fig.2Sensitivity distributions of the 180 degree spiral sensor

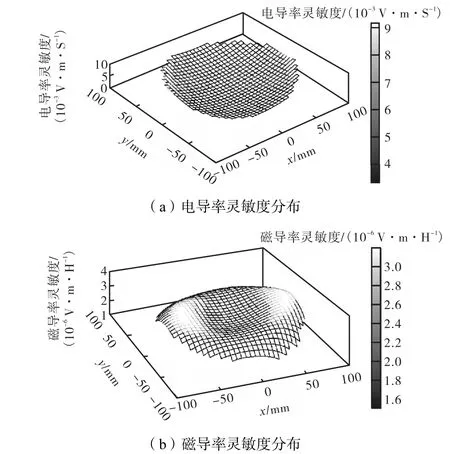
图3 360° 螺旋传感器灵敏度分布Fig.3 Sensitivity distributions of the 360 degree spiral sensor

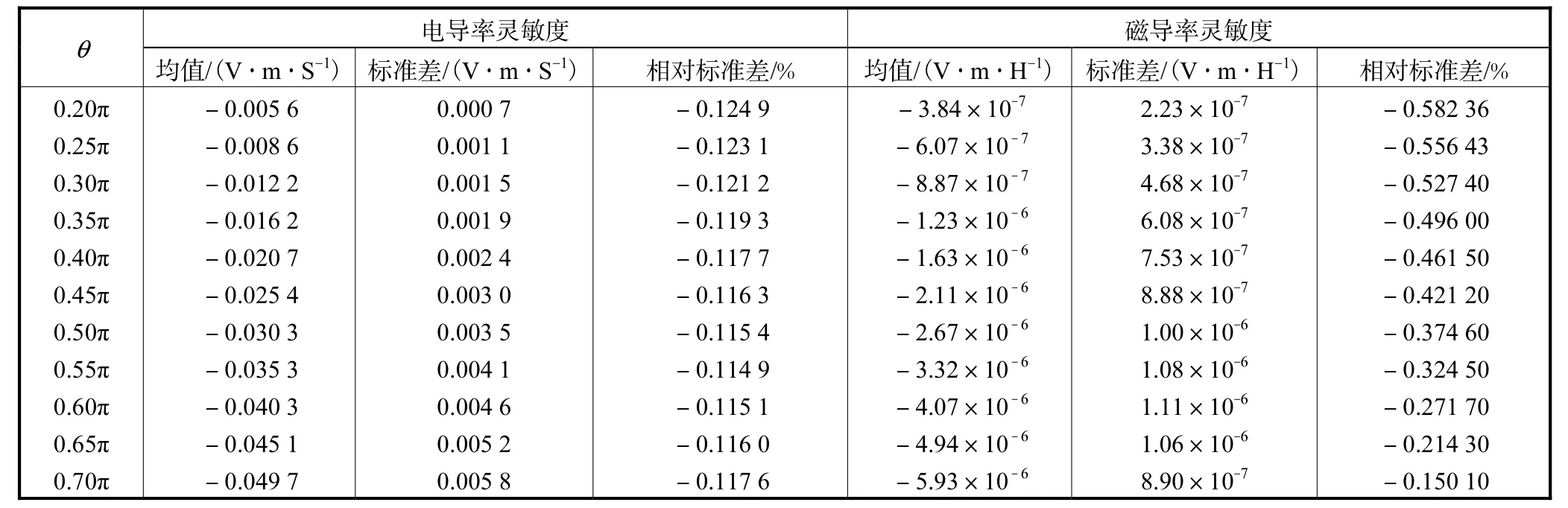
表1 180°螺旋传感器灵敏度的评估参数Tab.1 Estimation parameters of sensitivity of 180 degree spiral sensor

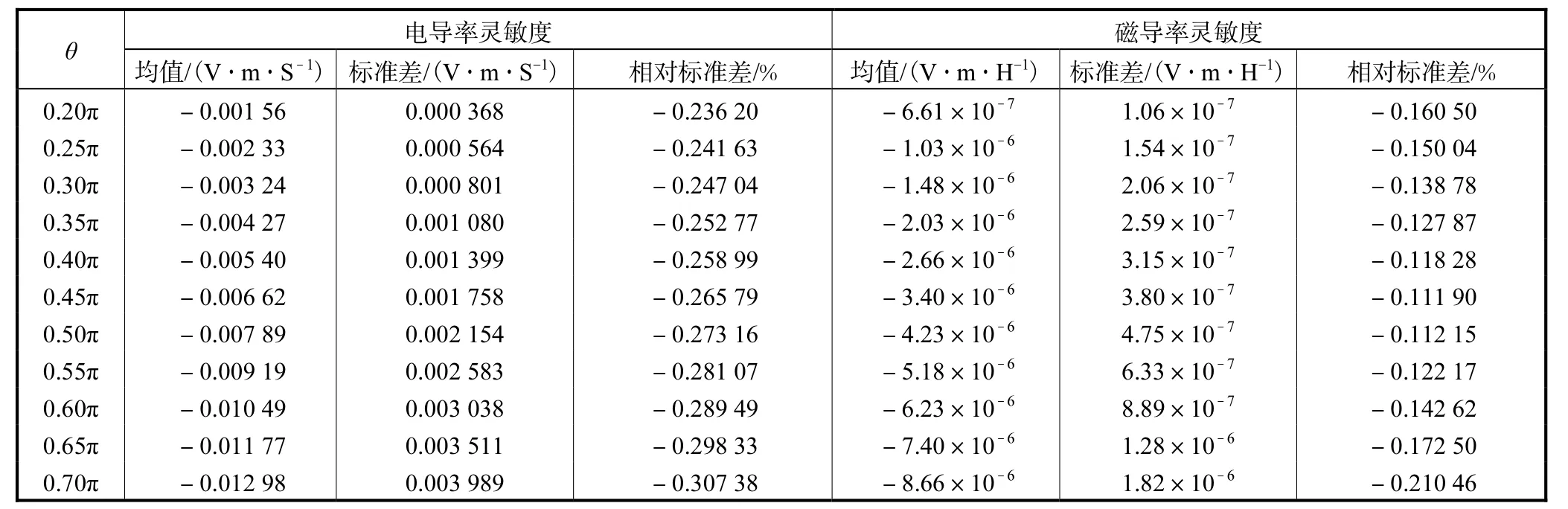
表2 360°螺旋传感器灵敏度的评估参数Tab.2 Estimation parameters of sensitivity of 360 degree spiral sensor

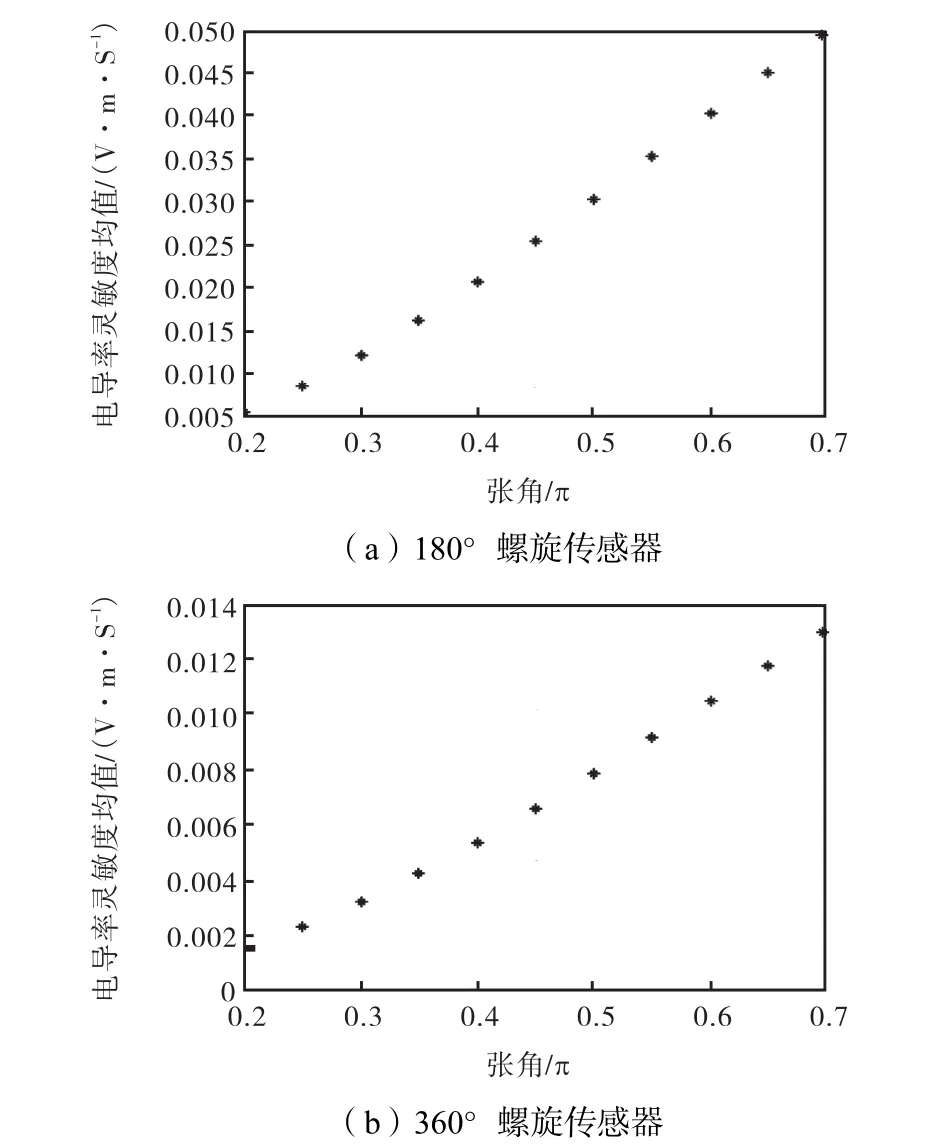
图4 电导率灵敏度均值与张角的关系曲线Fig.4 Relationships between the average conductivity sensitivity and θ of spiral sensors

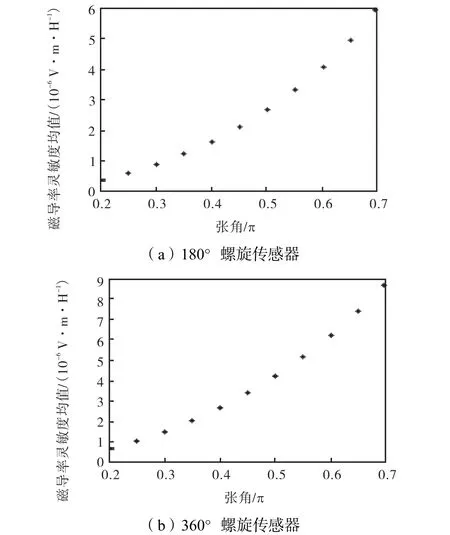
图5 磁导率灵敏度均值与张角的关系曲线Fig.5Relationships between the average permeability sensitivity and θ of spiral sensors

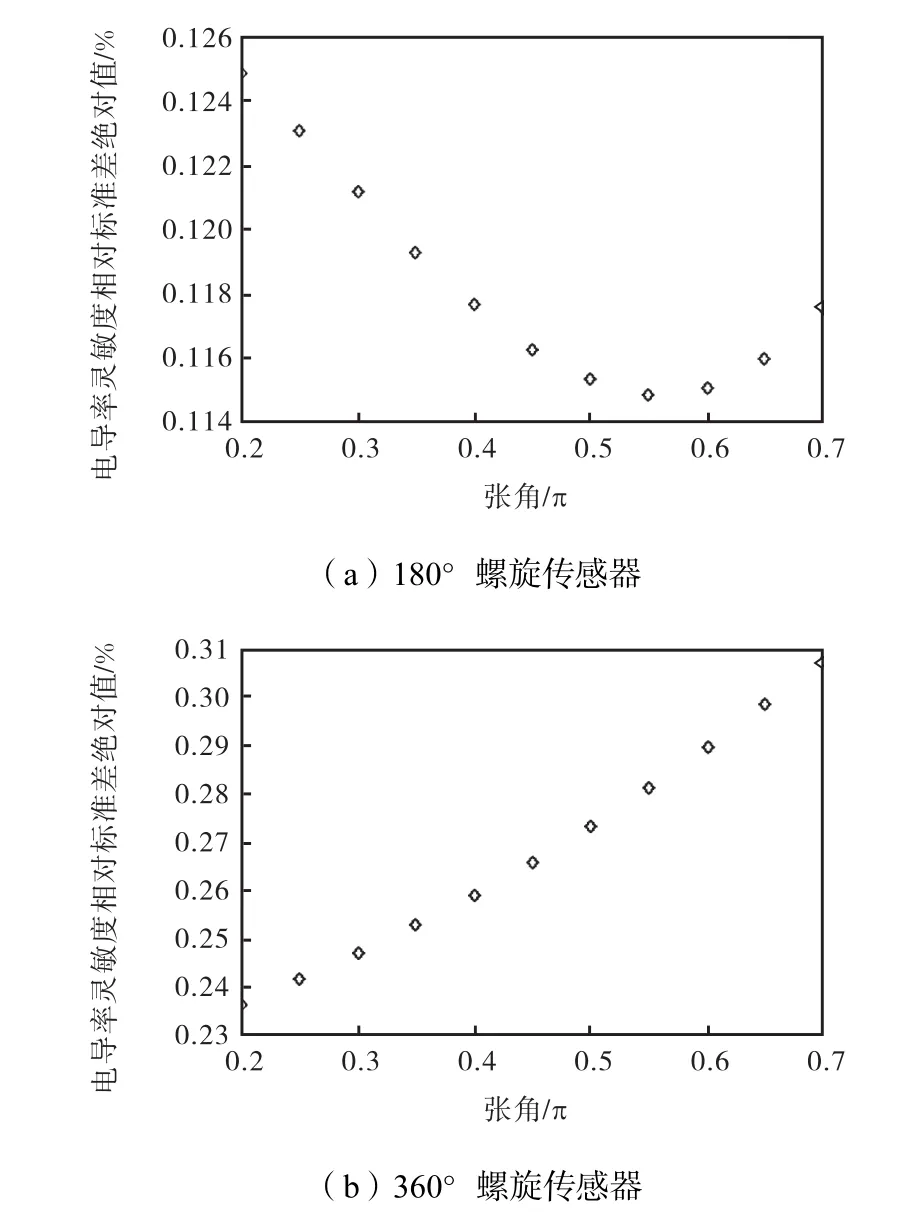
图6 电导率灵敏度相对标准差与张角的关系曲线Fig.6 Relationships between the conductivity sensitivity relative standard deviation and θ of spiral sensors

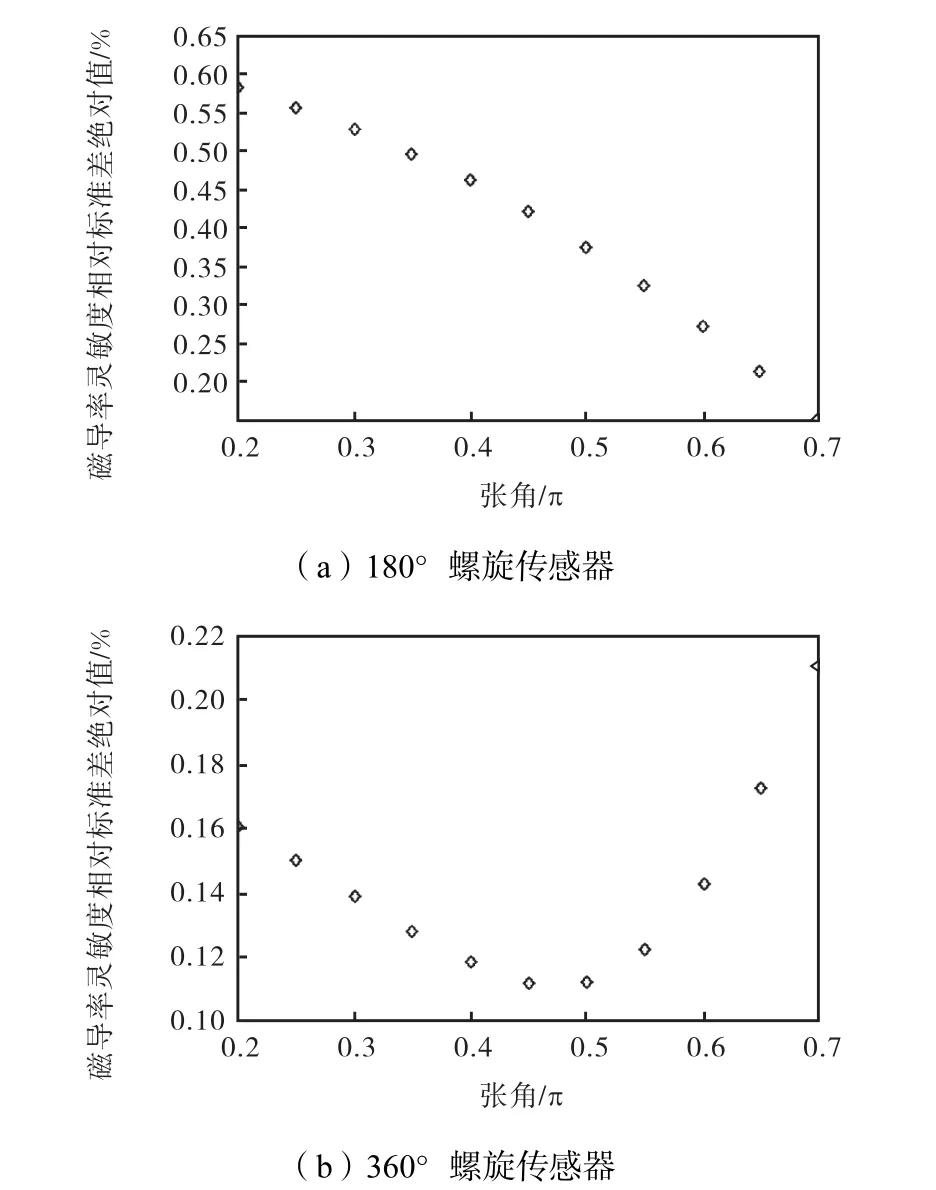
图7 磁导率灵敏度相对标准差与张角的关系曲线Fig.7 Relationships between the permeability sensitivity relative standard deviation and θ of spiral sensors

从图4～图7可以看出，对于180°螺旋传感器而言，随着θ的增大，不管是电导率灵敏度还是磁导率灵敏度的均值都随之增加，传感器灵敏度与张角近似呈线性关系．电导率灵敏度相对标准差随着θ的减小，在θ=0.55,π时达到最小值，而后又增大．磁导率灵敏度相对标准差则随着张角的增大逐渐减小．

对于360°螺旋传感器而言，随着θ的增大，不管是电导率灵敏度还是磁导率灵敏度的均值都随之增加．电导率灵敏度相对标准差随着张角的增加而逐渐增大．磁导率灵敏度相对标准差随着θ的增加先逐渐减小，在θ=0.45,π时达到最小值，而后又增大．

依据上面对灵敏度评估参数的说明，可知在实际应用中，需要同时考虑螺旋电磁传感器的灵敏性和均匀性，综合二者之后可以得到一个最优的传感器设计．在其他条件一定的前提下，180°螺旋传感器线圈的张角为0.55π时线圈测量性能最优；而360°螺旋传感器线圈的张角为0.45π时可使线圈测量性能最优．

3 静态实验

借助天津大学电磁层析成像硬件平台，配合新型的螺旋电磁传感器，进行了不同浓度下盐水的相含率测量实验．

如图8所示，天津大学螺旋电磁传感器相含率测量硬件平台由FPGA主控板、多级放大板、前端板、上位机4部分组成．其中FPGA主控板产生激励信号并进行逻辑控制、数据分析、上位机通讯等，多级放大板、前端板完成信号的驱动放大、信号检测、信号预处理、数据通讯等，最终在上位机进行实时显示．

图8 实验硬件Fig.8 Hardware for the experiment

被测物场为圆柱状，半径为37.5,mm，高度为100,mm．实验一共有2组，分别采用张角为0.30π的180°螺旋电磁传感器和张角为0.25π的360°螺旋电磁传感器，每个传感器的激励线圈和接收线圈都由2根铜丝缠绕而成．实验中采用不同相含率的盐水，设饱和盐水的导电率为1.0，则其他相含率的盐水导电率可以由其浓度求出．

通过实验可知，互感相角相对变化率对相含率的变化十分敏感，因此可将其选为相含率变化的电学敏感指标．其中互感相角值P、互感相角相对变化率Pr分别定义为

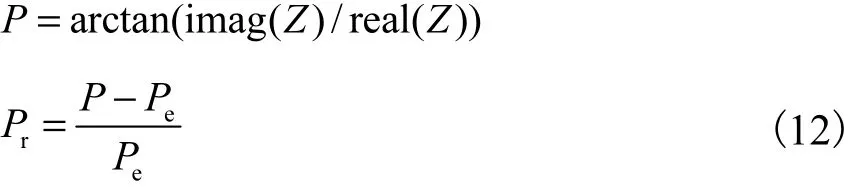
式中：imag(Z)、real(Z)分别为互感信号的虚部和实部；Pe为空场状态下的互感相角值；P为不同相含率对应的互感相角值．

分别将不同导电率的盐水溶液注入物场区域，相应测量得到不同相含率下的信号相角相对变化率，如表3所示．

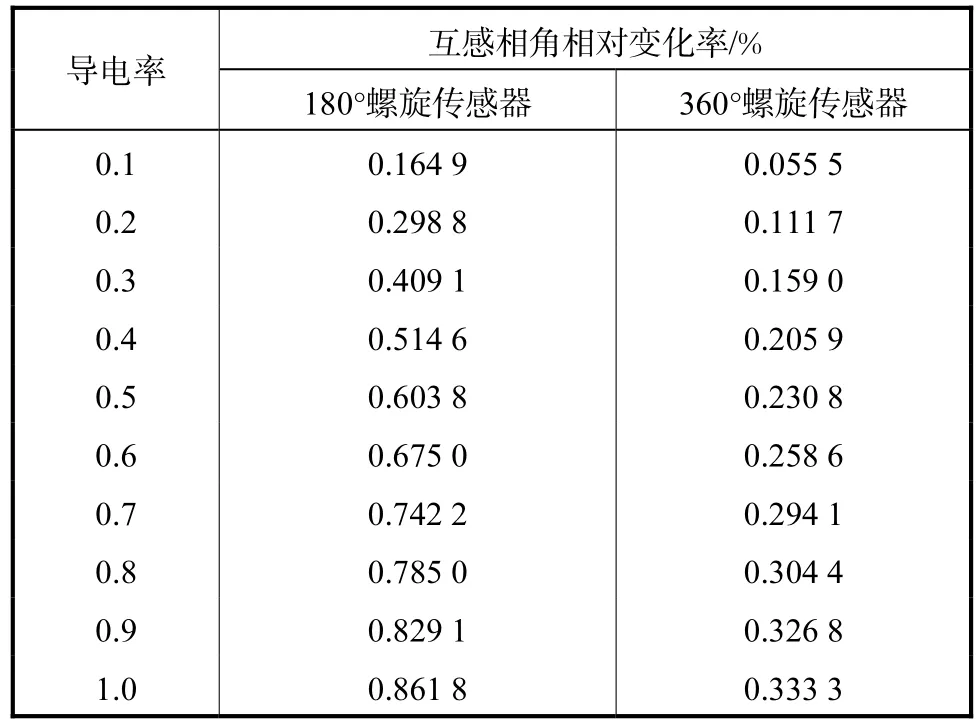
表3 不同相含率溶液的测量信号相角相对变化率Tab.3 Relative change ratios of phase angle versus different phase holdups

对上述实验数据，采用最小二乘法拟合，可标定得到天津大学螺旋传感器相含率测量平台的导电率与互感相角相对变化率的关系方程为

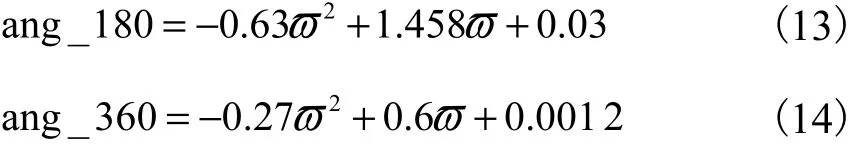
式中：ang_180和ang_360分别为180°螺旋电磁传感器和360°螺旋电磁传感器的互感相角相对变化率的百分数；ϖ为盐水溶液的导电率．拟合曲线如图9所示．

由图9可知，以互感相角相对变化率作为电学敏感指标能够很好地反映被测物场的相含率或导电率，两者的实验数据具有明显的相关特性．由此可知，对于特定的螺旋电磁传感器，经过数据标定即可得到该传感器相含率与相角相对变化率的关系曲线，从而可用于相含率的实时测量．

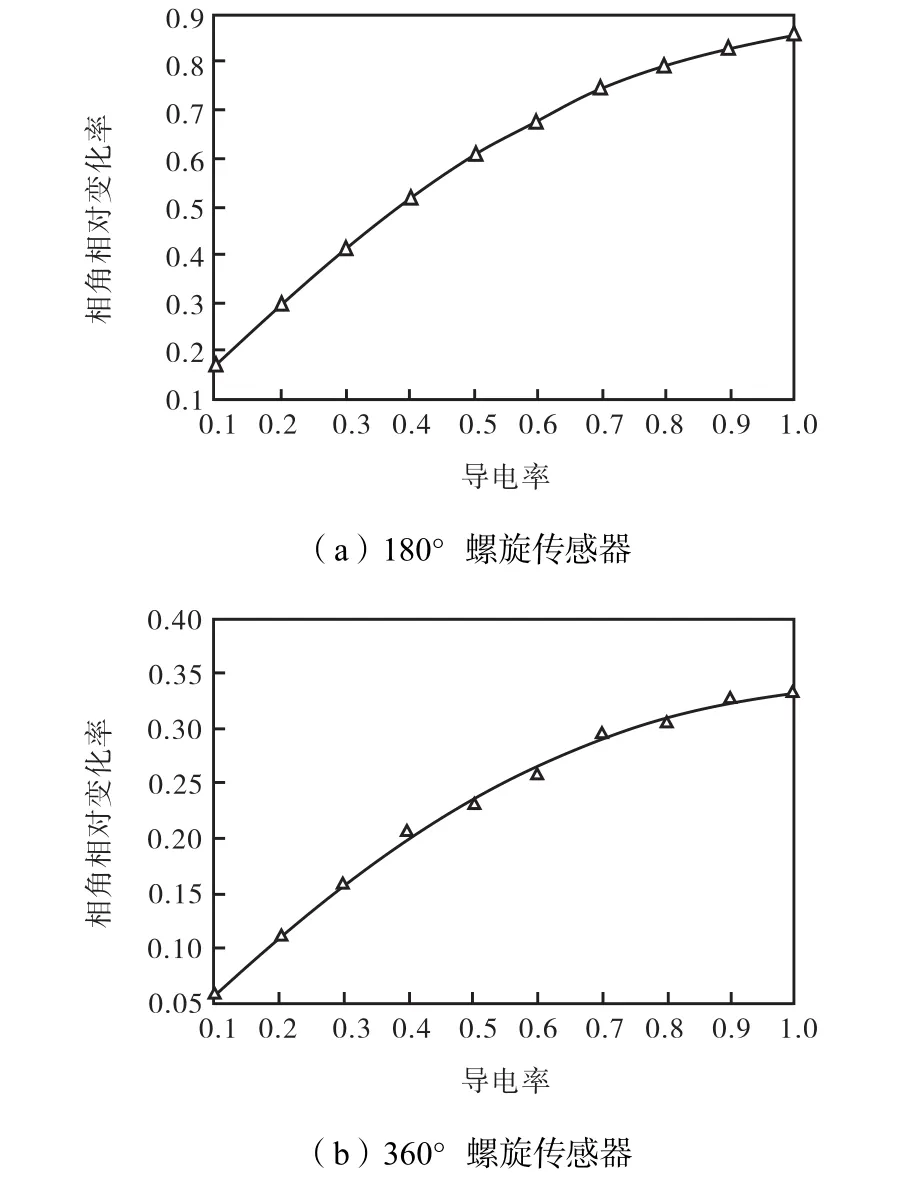
图9 螺旋传感器互感相角相对变化率和导电率拟合曲线Fig.9 Correlation curves between electric conductivity and the relative change ratio of the phase angle of two spiral sensors

4 结 语

螺旋电磁传感器是一种新型相含率测量传感器．螺旋传感器在管道截面均匀的灵敏度分布使得其用于相含率测量成为可能．

基于提出的灵敏度评价指标实现了螺旋传感器的结构优化．结果表明，随着张角的增加，180°和360°螺旋式结构的传感器的敏感性不断增强，并在特定张角下达到均匀性最优值．

通过硬件实验，验证了螺旋电磁传感器在相含率测量上的可行性和准确性．通过对实验数据拟合得到了该系统的标定曲线，建立了相含率与互感相角变化率的关系曲线，为相含率测量奠定了基础．

综上所述，螺旋电磁传感器不但具有非接触、非侵入、结构简单、检测快速等优点，还通过改进传感器结构改善了测量系统的敏感性和均匀性，在相含率测量上具有很大的优势和广阔的前景．

［1］ White B R，Mounla H. Two-phase measurements of saltating turbulent boundary layer flow [J]. InternationalJournal of Multiphase Flow，1982，8(5)：459-473.

［2］ Bourdel E，Pasquet D，Denorme P，et al. Measurement of the moisture content with a cylindrical resonating cavity in TM010 mode [J]. IEEE Transactions on Instrumentation and Measurement，2000，49(5)：1023-1028.

［3］ Fordham E J，Lenn C P，Holmes A，et al. Corrections of gradiomanometer data for volume fractions in twophase flows [J]. Measurement Science and Technology，1999，10(12)：131-135.

［4］ Tollefsen J，Hammer A. Capacitance sensor design for reducing errors in phase concentration measurements [J]. Flow Measurement and Instrumentation，1998，9(1)：25-32.

［5］ Mwambela A J，Johansen G A. Multiphase flow component volume fraction measurement：Experimental evaluation of entropic thresholding methods using an electrical capacitance tomography system [J]. Measurement Science and Technology，2001，12(8)：1092-1101.

［6］ Devia F，Fossa M. Design and optimization of impedance probes for void fraction measurements [J]. Flow Measurement and Instrumentation，2003，14(4/5)：139-149.

［7］ Lucas G P，Panaqiotopoulos N. Oil volume fraction and velocity profiles in vertical，bubbly oil-in-water flows [J]. Flow Measurement and Instrumentation，2009，20(3)：127-135.

［8］ 薛 婷，曹兆峰，邹晨生，等. 热扩散式油水两相流相含率测量方法[J]. 天津大学学报，2011，44(5)：396-400.

Xue Ting，Cao Zhaofeng，Zou Chensheng，et al. Heatdiffusion method of phase volume fraction measurement in oil/water two-phase flow[J]. Journal of Tianjin University，2011，44(5)：396-400(in Chinese).

［9］ 徐清华. 管道原油含水率测量技术的研究[D]. 沈阳：沈阳工业大学信息科学与工程学院，2010.

Xu Qinghua. Study of Measuring Technique on Pipeline Water Content of Crude Oil [D]. Shenyang：School of Information Science and Engineering，Shenyang University of Technology，2010(in Chinese).

［10］ Yu Z Z，Peyton A J，Xu L A，et al. Electromagnetic inductance tomography(EMT)：Sensor，electronics and image reconstruction algorithm for a system with a rotatable parallel excitation field [J]. IEE Proc - Sci Meas Technol，1998，145(1)：20-25.

［11］ Yin W，Peyton A J. A planar EMT system for the detection of faults on thin metallic plates [J]. Measurement Science and Technology，2006，17(8)：2130-2135.

［12］ Yin W L，Binns R，Dickinson S J. Analysis of the liftoff effect of phase spectra for eddy current sensors[C]//Instrumentation and Measurement Technology Conference. Ottawa，Canada，2005：1779-1784.

［13］ Griffiths H. Magnetic induction tomography [J]. Measurement Science and Technology，2001，12(8)：1126-1131.

［14］ Yin W L，Peyton A J，Stefani F. Theoretical and numerical approaches to the forward problem and sensitivity calculation of a novel contactless inductive flow tomography(CIFT)[J]. Measurement Science and Technology，2009，20(10)：105503. 1-105503. 7.

［15］ Dyck D N，Lowther D A，Freeman E M. A method of computing the sensitivity of electromagnetic quantities to changes in materials and sources [J]. IEEE Transactions on Magnetics，1994，30(5)：3415-3418.

［16］ Yin W L，Dickinson S J，Peyton A J. Evaluating the permeability distribution of a layered conductor by inductance spectroscopy [J]. IEEE Transactions on Magnetics，2006，42 (11)：3645-3649.

［17］ 尹武良. 低频电磁传感检测技术[M]. 北京：科学出版社，2010.

Yin Wuliang. Low Frequency Electromagnetic Sensing Detection Technology[M]. Beijing：Science Press，2010(in Chinese).

［18］ 徐 凯，陈 广，尹武良，等. 基于场量提取法的电磁层析成像系统的灵敏度推算[J]. 传感技术学报，2011，24(4)：543-547.

Xu Kai，Chen Guang，Yin Wuliang，et al. Sensitivity derivation and calculation of electromagnetic tomography(EMT)sensor based on field value extraction [J]. Chinese Journal of Sensors and Actuators，2011，24(4)，543-547(in Chinese).

［19］ 冯慈璋. 电磁场[M]. 北京：高等教育出版社，1983.

Feng Cizhang. Electromagnetic Field[M]. Beijing：Higher Education Press，1983(in Chinese).

(责任编辑：孙立华)

Optimal Design of Spiral Electromagnetic Sensor for Phase Holdup Measurement

Zhao Qian，Xu Kai，Yin Wuliang
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Electromagnetic sensors can obtain the distributions of the medium through excitation and sensing coils distributed on the boundary. In this paper，a novel spiral electromagnetic sensor was proposed for phase holdup measurement. The sensitivity matrices of the spiral sensors of 180 and 360 degrees rotation were derived based on field theory and the design was optimized based on sensitivity analysis. The trends and rules for selecting the optimum parameters were obtained. The optimized spiral electromagnetic sensors have better and more homogenous sensitivity distributions. The experiment showed that the electric signals obtained were good indicators of the phase holdup. The correlation curves between phase holdup and the relative change ratio of the phase angle of spiral sensors were obtained which proved the feasibility and accuracy of the phase holdup measurement by the spiral electromagnetic sensors.

electromagnetic detection；phase holdup；spiral electromagnetic sensor；sensitivity

TK212

A

0493-2137(2014)03-0205-07

10.11784/tdxbz201207017

2012-07-04；

2012-09-07.

国家自然科学基金国际重大合作资助项目(60910001)；教育部博士点基金资助项目(20090032110062).

赵 倩（1987— ），女，博士研究生，shmilyshenzhen@163.com.

尹武良，wuliang.yin@gmail.com.