A drifting trajectory prediction model based on object shape and stochastic motion features*

WANG Sheng-zheng (王胜正), NIE Hao-bing (聂皓冰), SHI Chao-jian (施朝健)

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, E-mail: szwang.smu@gmail.com

A drifting trajectory prediction model based on object shape and stochastic motion features*

WANG Sheng-zheng (王胜正), NIE Hao-bing (聂皓冰), SHI Chao-jian (施朝健)

Merchant Marine College, Shanghai Maritime University, Shanghai 201306, E-mail: szwang.smu@gmail.com

(Received April 13, 2014, Revised July 24, 2014)

There is a huge demand to develop a method for marine search and rescue (SAR) operators automatically predicting the most probable searching area of the drifting object. This paper presents a novel drifting prediction model to improve the accuracy of the drifting trajectory computation of the sea-surface objects. First, a new drifting kinetic model based on the geometry characteristics of the objects is proposed that involves the effects of the object shape and stochastic motion features in addition to the traditional factors of wind and currents. Then, a computer simulation-based method is employed to analyze the stochastic motion features of the drifting objects, which is applied to estimate the uncertainty parameters of the stochastic factors of the drifting objects. Finally, the accuracy of the model is evaluated by comparison with the flume experimental results. It is shown that the proposed method can be used for various shape objects in the drifting trajectory prediction and the maritime search and rescue decision-making system.

sea-surface object searching, drifting model, drifting trajectory prediction, maritime search and rescue

Introduction

Rapidly approaching a drifting object is an important task in the marine search and rescue program. However, a drifting object is moving under the action of the net balance force acting on it from wind, currents and waves. Unless the trajectory or the most probable search area of the drifting object is predicted accurately, it would be difficult to find the drifting object. Theoretically speaking, it is possible to compute the evolution of the search area of any drifting object against time given all kinds of unknowns including the last known position, the object type and wind, waves, and currents affecting the motion of the object. In practice, however, it is difficult to design a mathematical model to predict the trajectories of the drifting objects because of the irregular shape of real-world objects and the stochastic motion of the objects resulted from wind, waves and currents.

Therefore, over the past two decades, how to model the motion of a drifting object is always a research focus. Early studies focused on the LEEWAY method, a typical drifting model applied to compute the movements of the drifting objects. This model provides a basic principle of the object drifting, however, in actuality, there are many unknowns, such as the shape, the appearance, the weight of the object, the sea-states etc., so the model is limited to some simple applications. Breivik et al.[1]obtained the relationships between the drifting velocity of the LEEWAY and the real wind field by observing and recording the movements of the total 63 different categories of objects, and the related equation in the downwind and crosswind frames of reference for these 63 categories. They selected proper parameters from these experimental results to estimate the motion of the similar objects. In this method, a large error might be resulted due to the variability of the buoyancy and the initial state of the similar drifting objects, which limits the operational application of this method. On that basis, the Norwegian Meteorological Institute (NMI) developed the LEEWAY-based drifting model that was widely applied in the maritime SAR center, the marine traffic service and the environmental protection authorities[2],but this system mainly was used in the ship drifting model and for the oil spill fate modeling.

In practice, there is a large ingredient of chance involved in the calculation of the object motion on the sea-surface[3-12]. Therefore, Hong et al.[13]employed Markov Chain to convert the drift trajectory prediction problem into a shortest path problem with the probability function as the weight of the model. Their model improved the searching accuracy and effectiveness, but the computational cost limited its application. Ni et al.[14]proposed a theoretical model for predicting the boat drift in search and rescue missions. The uncertainty of the boat drift was evaluated by interval analysis of the uncertainties of the characteristics of the drifting boat and external forcing fields. Breivik et al.[15]studied the leeway (windage) of five typical SAR/HAZMAT objects (person in water, mine, small sailboat, small open boat and a 20-feet container), In their experiments, the leeway was decomposed into downwind and crosswind components for every 10 min sample. The linear regression model was built both unconstrained and constrained through the zero and the linear regression parameters were used in the SAR planning tools. Isobe et al.[16]also observed the drifting of the objects in the flume experiments and derived a formulation of the leeway parameters to compute the leeway drift speed. Breivik et al.[1]proposed a method for conducting leeway field experiments to establish the drift properties of small objects (0.1 m-25 m) . The objective was to define a standardized and unambiguous procedure for condensing the drift properties down to a set of coefficients to be incorporated into existing stochastic trajectory forecast models for drifting objects of concern in search and rescue operations and other activities involving vessels lost at sea such as containers with hazardous material.

Although the above-described techniques were successfully applied partially in some maritime search and rescue systems to assist operational users in forecasting the searching area, there are many limitations in these methods, which suffer at least in two aspects. (1) the geometry structure properties were not integrated into the model so that the system only tackled the specified objects and lacked the generality, (2) a large number of stochastic motion features were not involved in the model that affected the accuracy of the drifting trajectory predictions.

In order to better model the movements of the drifting object, this paper proposes a novel method to integrate the shape properties of the objects into the model by using the weight coefficient vector that may be extracted from the experimental parameters. Then the probability functions of the uncertainty parameters are employed to simulate the stochastic motions of the objects, and two objects are tested under different external conditions.

1. Drifting trajectory model based on object shape and stochastic motion

1.1Object shape analysis

In the drifting process, the movements of the objects in downwind and crosswind would be disturbed due to the inhomogeneous action of the external forces from wind, current and waves.

(1) Object shape features

Generally, the objects in search and rescue (SAR) and hazardous material (HAZMAT) have various shape and size. The leeway of 63 categories of objects, such as people, life raft, sailing, boat, fishing boats (small and large commercial fishing vessels), sport boat, container, tank and so on, was studied by Breivik et al.[1]. They identified parameters for the leeway speed as a function of the wind speed and a leeway divergence angle for all 63-leeway categories, and studied the leeway (windage) of five typical SAR/ HAZMAT objects (person in water, mine, small sailboat, small open boat and a 20-ft container). The relationships between the leeway speed and the object shape of all categories of objects are summarized, and it is shown that all categories of objects could be classified into two categories (sphere and square) in terms of the shape features.

Fig.1 The objectʼs shape affects its drift and its leeway divergence

The stochastic extent of the spherical objects is less than that of the square objects, and the disturbances of the drifting motion of the spherical objects under the different initial state are in a uniform distribution. Furthermore, the leeway divergence angle of the spherical objects changes only slightly with the wind/current disturbances and can keep in a stable range. On the other hand, the disturbances of the trajectory of the square objects are large and stochastic. Therefore, we will discuss the relationships between the initial state of the square objects and the direction of the external forces.

(2) Stochastic disturbance of the square object

For a square object, as shown in Fig.1, the angleθbetween the long axis of the object and the wind direction would influence the next direction of the deviation of the object. Whenθ∈ (0o,90o) ∪(180o, 270o), the next direction is to the left of the downwind direction, and whenθ∈ (90o,180o) ∪ (270o,360o), the next direction is to the right of the downwind direction.

However, the initial angleθis unknown when we compute the drifting direction. Hence we have to simulate the stochastic process of the change of the angleθbased on the statistic analysis results of the various drifting objects.

1.2Drifting trajectory prediction model

whereρais the air density,Cais the drag coefficient of the wind force,Aais the area of the exposed above-water part of the object,Vwis the wind speed.

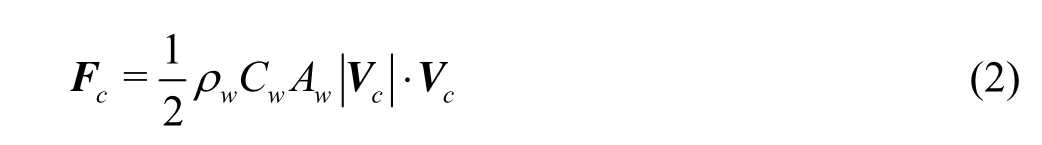
whereρwis the density of the seawater,Cwthe drag coefficient of the ocean current,Awis the area of the submerged part of the object,Vcis the current speed.

Without the action of the wave force, the drift would eventually reach a stable drifting speedVounder the action of the relative wind and current drag forces. The drag force of the wind depends on the relative wind speedVw-Vopassing the object, and the drag force of the current depends on the relative current speedVo-Vcpast the object. According to the law of motion, these two forces must be equal in magnitude and opposite in direction, and therefore the balance equation can be deduced with respect to these two forces, and is written as follows.

whereLais the effective length of the object,Cwavis the thrust coefficient of the wave,His the amplitude of the wave (generally is half of the wave height), andφis the encounter angle of the wave.

Hence, the total balance equation of the drifting motion can be written as

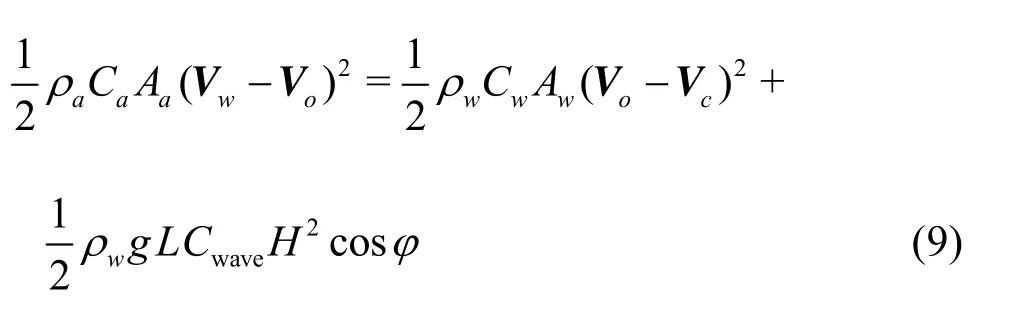
The stable average drifting speed can be obtained by solving Eq.(9), as

However, according to Ref.[14,18], the impact of the waves on the drift can be ignored when the wave amplitude is much less than one 1/30th of the length of the object. Otherwise, the wave might significantly affect the coefficientλ. The reason is that the wave can change the area of the boat surface exposed to wind and current. It can also produce a local wind drift current.

Therefore, the drifting speed of the object changes dynamically, since the coefficientλ, the encounter angleφof the wave or the divergence angleθwill change with the evolution of the drifting motion. Thus, the stochastic disturbance resulted from wind and current effects is considered, and the real-time drifting speed of the object is expressed as

where ΔUis a stochastic perturbation of the drifting speed resulted from the effects of non-homogeneous external forces brought about by wind and current, which will be discussed in the next section.

Finally, the real-time speed of the drifting object can be calculated by integrating all probability density functions and substituting the coefficient vector into the model, with the assumption that the initial position isP(0), the next position isP(1) after elapsing time Δt, then

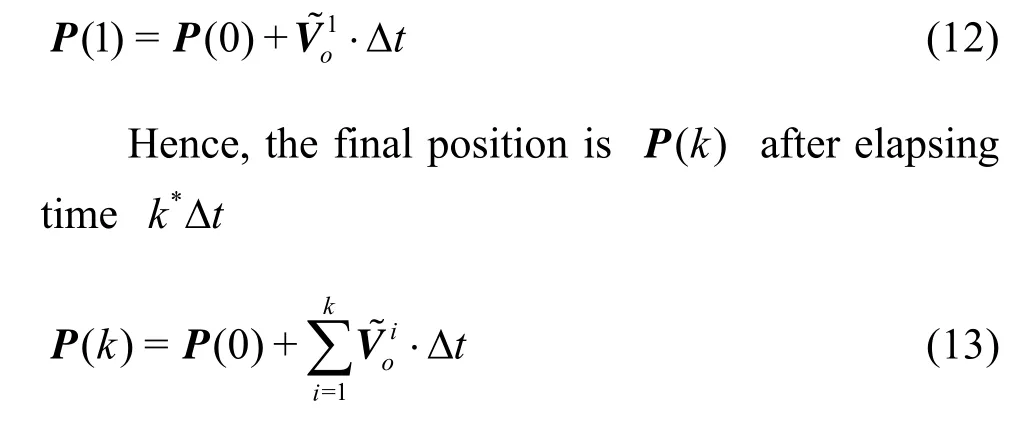
1.3Uncertainty analysis of the drifting model

As shown in Fig.2,ais the equivalent width of the square object,bdenotes the equivalent length of the square object,1θis the divergence angle between the principal axis of the object and the wind direction, 2θis the divergence angle between the principal axis of the object and the current direction.

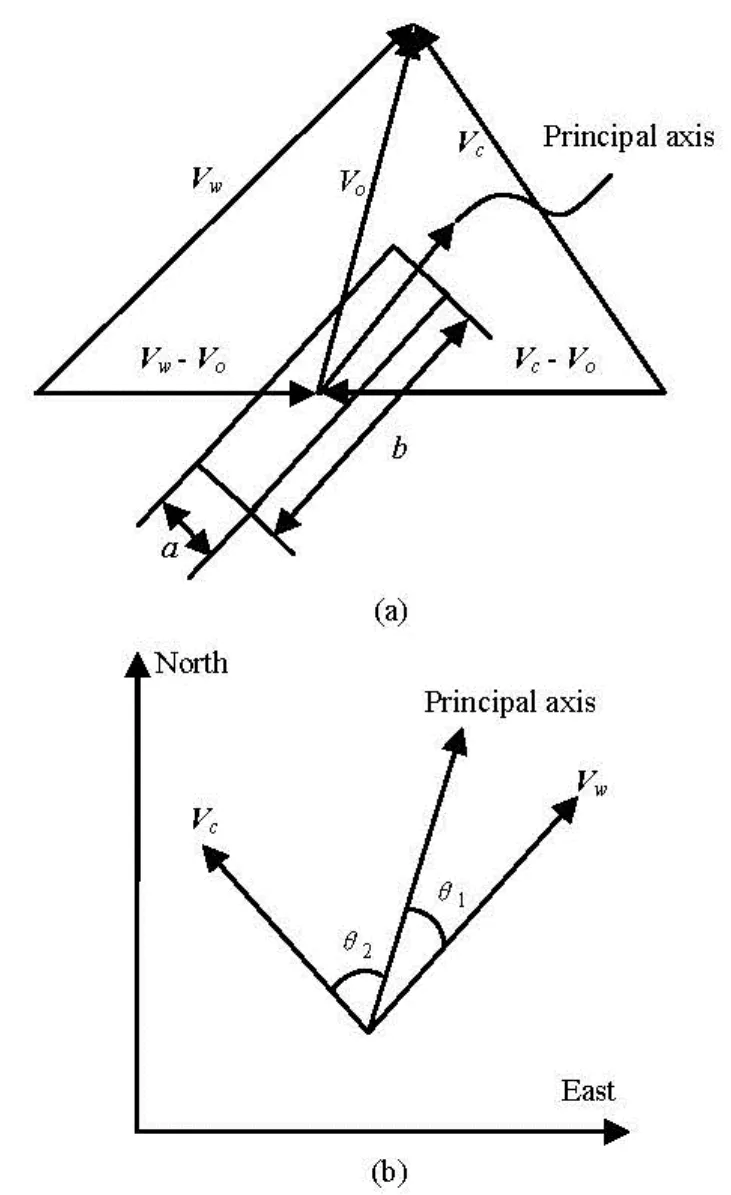
Fig.2 The relationships beween the wind/current direction and the principal axis of the object

The drifting speed of the object would continuously change due to the change of the effective action area of wind/current on the surface area of the object.

The stochastic perturbation speed can be determined as shown in Ref.[19], as

Besides the shape properties of the object, there is another issue to be considered. Each input variable of the model cannot always be the same in practice during the drifting process. Some variables such as the ratio of immersion and the divergence angleθare changing. Here we use the idea of the stochastic process to deal with this issue.

Fig.3 Different divergence angles under different time

For the divergence angle, as shown in Fig.3, the angle between the principal axis of the object and the wind/current will change with the moving of the drifting object. The prior distribution of the angleθobeys a uniform distributionθ～ ∪ (0,π) by observing the motions of different objects, the probability densityf(θ) is given by

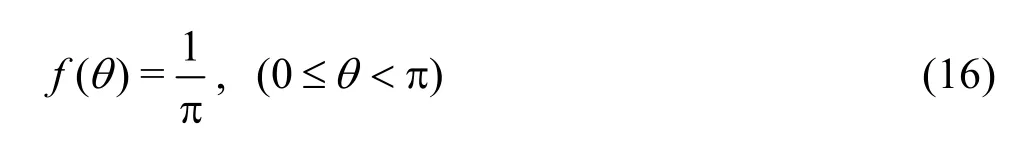
For the immersion ratioRA, as shown in Fig.4, the exposed above-water part of the object will repeatedly change with the motion of the object, and this process is stochastic. However, its change obeys a normal distribution and can be defined as

whereμAis the mean value,σAis the standard deviation.

The probability densityφ(RA) ofRAcan be determined as

1.4Model optimization

The motion of the object is not only related to the oceanographic conditions, but also to the geometrical structure features of the object. The objects of different shapes have different trajectories under the same external conditions. The reason is that the directions and the actions of the external drag force are different for different drifting objects. In this paper, we propose to use a weight for each variable that affects the drifting velocity of the object. The basic idea of the definition of the weight is to make the residual of each variable positively correlated to the shape properties of the object, reducing the impact caused by different objectsʼ shapes on the real-time drifting speed and thus making the average speed to some extent robust to this variation between objects.

Fig.4 Different immersion ratios under different time

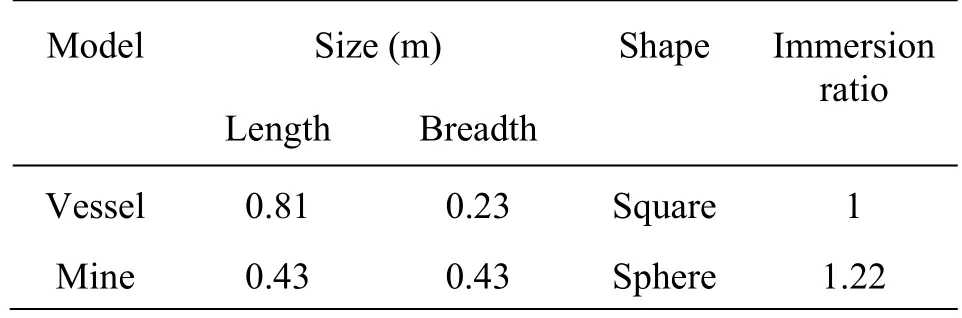
Table 1 Some properties of two models

Fig.5 The experiments under different environmental conditions

Fig.6 The real-time and averaged speeds (v/ms-1) of the drift under the current only by simulating the drifting of the object

The strategy is to find an optimal combination of the ocean and atmospheric models based on past/ a priori information, and use the derived optimal weights to compute new predictions in a forecast process. There are many methods to retrieve these optimal weights. The most straightforward is to use a linear regression from a least squares approximation.

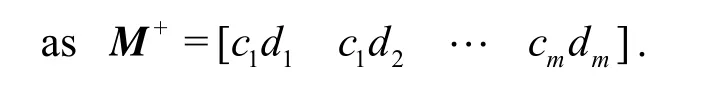
2. Experiments and results

To demonstrate the performance of our drifting trajectory prediction algorithm and evaluate the contributions of the components in the proposed approach, we conduct comprehensive experiments on two typical classes (sphere and square models), and compare the achieved results with the observed experimental results. Table 1 shows the basic properties of two models, and the general model parametersCw=2.563× 10-3,Ca=0.865× 10-3.

The weight coefficient vector can be estimated by using least squares regression method to analyze the experimental data in Ref.[1]. Here we obtain the weighted coefficient vectorAof the input vector

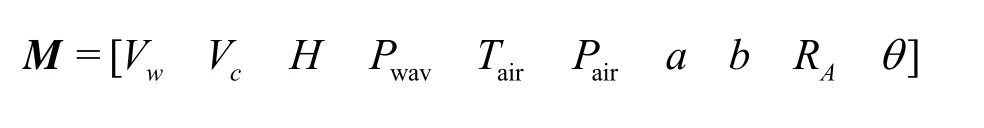
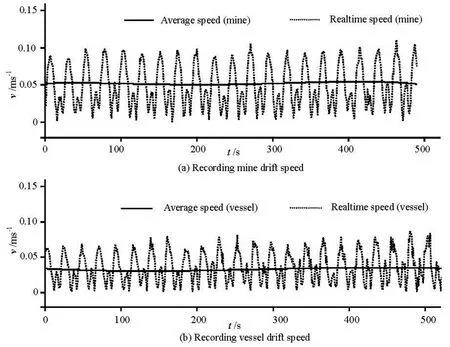
Fig.7 The real-time and averaged speeds of the drift under the current and waves (current speed: 0.3 m/s)

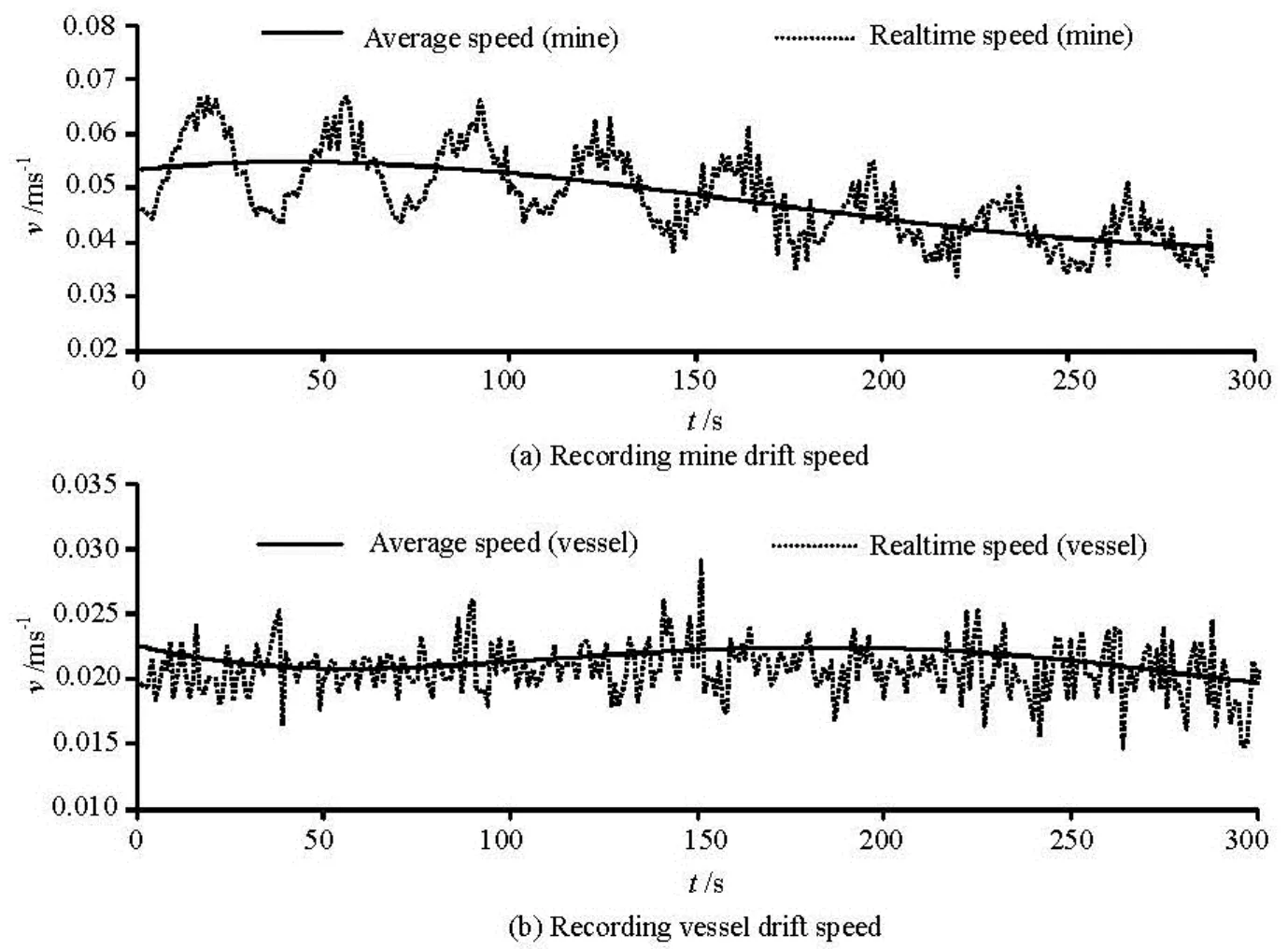
Fig.8 The real-time and averaged speeds of the drift under wind, currents and waves (wind speed: 3.5 m/s, wave height 0.08 m)

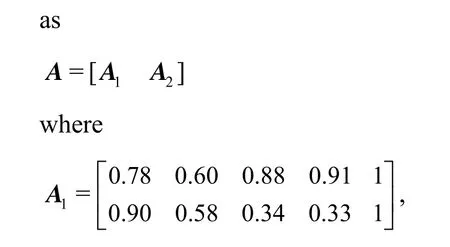
The 1strow and 2strow ofAis the weight coefficient vector of the mine and vessel models, respectively, andPwavdenotes the period of the wave,Tairdenotes the air temperature, andPairdenotes the pressure of the air.

As shown in Fig.6, the stochastic disturbance of the real-time speedvof the square vessel model is larger than that of the sphere mine model. The reason is that the disturbance speed ΔUof the mine is different from that of the vessel model when the stochastic changes of the divergence angleθare under the same external conditions, as is explained in Eq.(14). In addition, the average speed of the square vessel model is less than that of the sphere mine model that accounts for the influence of the shape features on the drift under the same external conditions. Here, the weight coefficient vector is used to simulate the relationships between the drifting speed and the shape properties.

As shown in Fig.7, waves are added into the experiments, but the average speed of the drift keeps a similar speed in the above experiment(See Fig.6). As shown in Fig.8, wind, currents and waves are added into the experiment, which leads to apparent changes.

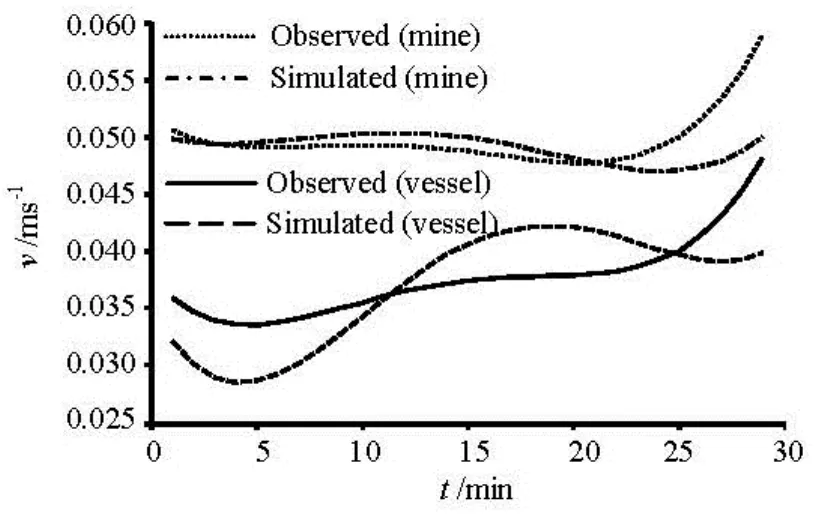
Fig.9 Comparisons between the observed speeds and the simulated speeds for two kinds of objects

Fig.10 Comparisons between the observed trajectory and the simulated trajectory under the current only

The simulated averaged speeds are compared with the observed speeds. It is apparent that the simulated speed as a whole agree quite well with the observed values, as shown in Fig.9.

Experiments are designed to check the effectiveness by comparing the simulated trajectory and the observed trajectory of the drifts. As shown in Fig.10,xdenotes the distance of the downwind direction, andyis the distance of the crosswind direction, under the current only, the experimental results of the vessel and the mine are consistent with the predicted trajectories and the observed trajectories, and the drifting objects keep stably moving toward the initial direction.

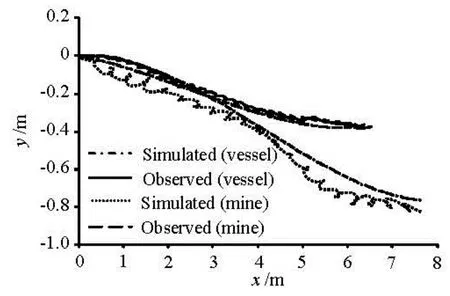
Fig.11 Comparisons between the observed trajectory and the simulated trajectory under wind, waves and currents

After wind and waves are added into the system, both of trajectories diverge stochastically in the crosswind direction, but the simulated trajectory as a whole agrees with the observed trajectory, as shown in Fig.11.

3. Conclusions

This paper proposes some novel methodologies to carry out the simulation of the real-time speed of the drifting objects. The shape properties are embedded into the system to calculate the real-time speed to improve the accuracy of the average speed of the drift, and the weight coefficient vector is designed to describe the relationships between the shape properties and the stochastic motion of the object. Furthermore, the stochastic distribution density functions of the input variables are used to simulate the real-time state of the drifting objects, which provides estimations of the unknown variables.

In order to validate the effectiveness of the proposed method, experiments are designed to compare the simulated speed and trajectories with the observed. The experimental results show that the simulated speed agrees well with the observed speed in both the vessel and the mine model experiments. Thus, the trajectory of the drifting object can be predicted accurately.

先对种子进行预处理再播种能有效提高种子的发芽率。对于农民自繁自留的种子，形状上大多都层次不齐，有的还掺混着少量的杂种，甚至还有带病虫的籽粒。因此，播种前筛选一遍，可以保证种子质量，为小麦发苗奠定基础。

The proposed method provides an effective means to predict the drifting trajectory and can beapplied in the drifting trajectory prediction and the maritime search and rescue decision-making system. Further validation experiments on the open sea are needed.

Acknowledgment

The authors would like to thank editors and anonymous reviewers for their comments and suggestions, which helped improving the quality of this work greatly.

[1] BREIVIK Ø., ALLEN A. and CHRISTOPHE M. et al. Wind-induced drift of objects at sea: The leeway field method[J]. Applied Ocean Research, 2011, 33(2): 100-109.

[2] HACKETT B., BREIVIK Ø. and WETTRE C. Ocean Weather Forecasting: An integrated view of oceanography[M]. Berlin, Germany: Springer-Verlag, 2006, 507-524.

[3] GASTGIFVARS M., LAURI H. and SARKANEN A. et al. Modelling surface drifting of buoys during a rapidly-moving weather front in the Gulf of Finland, Baltic Sea[J]. Estuarine, Coastal and Shelf Science, 2006, 70(4): 567-576.

[4] KOD S., MARTIN P. J. and ROWLEY C. D. et al. A real-time coastal ocean prediction experiment for MREA04[J]. Journal of Marine Systems, 2008, 69(1-2): 17-28.

[5] ULLMANN D. S., O'DONNELL J. and KOHUT J. Trajectory prediction using HF radar surface currents: Monte Carlo simulations of prediction uncertainties[J]. Journal of Geophysical Research, 2006, 111(C12): 1-14.

[6] DANIEL P., JAN G. and CABIOC＇H F. et al. Drift modeling of cargo containers[J]. Spill Science and Technology Bulletin, 2002, 7(5-6): 279-288.

[7] ESSEN H. H., BREIVIK Ø. and GUNTHER H. et al. Comparison of remotely measured and modeled currents in coastal areas of Norway and Spain[J]. The Global Atmosphere-Ocean System, 2003, 9(1-2): 39-64.

[8] MONBETA V., AILLIOTA P. and PREVOSTOB M. Survey of stochastic models for wind and sea state time series[J]. Probabilistic Engineering Mechanics, 2007, 22(2): 113-126.

[9] VANDENBULCKE L., BECKERS J. M. and LENARTZ F. et al. Super-ensemble techniques: Application to surface drift prediction[J]. Progress in Oceanography, 2009, 82(3): 149-167.

[10] RIXEN M., FERREIRA-COELHO E. Operational surface drift prediction using linear and non-linear hyperensemble statistics on atmospheric and ocean models[J]. Journal of Marine Systems, 2007, 65(1-4): 105-121.

[11] DAVIDSON F., ALLEN A. and BRASSINGTON G. et al. Applications of GODAE ocean current forecasts to search and rescue and ship routing[J]. Oceanography, 2009, 22(3): 176-181.

[12] EIDE M., ENDRESEN Ø. and BREIVIK Ø. et al. Prevention of oil spill from shipping by modelling of dynamic risk[J]. Marine Pollution Bulletin, 2007, 54(10): 1619-1633.

[13] HONG S. P., CHO S. J. and PARK M. J. et al. Optimal search-relocation trade-off in Markovian-target searching[J]. Computers and Operations Research, 2009, 36(6): 2097-2104.

[14] NI Z., QIU Z. and SU T. On predicting boat drift for search and rescue[J]. Ocean Engineering, 2010, 37(13): 1169-1179.

[15] BREIVIK Ø., ALLEN A. An operational search and rescue model for the norwegian sea and the north sea[J]. Journal of Marine Systems, 2008, 69(1-2): 99-113.

[16] ISOBE A., HINATA H. and KAKO S. et al. Interdisciplinary studies on environmental chemistry marine environmental modeling and analysis[M]. Tokyo, Japan: TERRAPUB, 2011, 239-249.

[17] BREIVIK Ø., SATRA Ø. Real time assimilation of HF radar currents into a coastal ocean model[J]. Journal of Marine Systems, 2001, 28(3-4): 161-182.

[18] ABDALLA S., CAVALERI L. Effect of wind variability and variable air density on wave modeling[J]. Journal of Geophysical Research. 2002, 107 (C7): 1-17.

[19] NIE H. B. MCMC-based drifting trajectory prediction model and dynamic optimizing ship routeing algorithm[D]. Master Thesis, Shanghai, China: Shanghai Maritime University, 2013(in Chinese).

10.1016/S1001-6058(14)60104-9

* Project supported by the National Natural Science Foundation of China (Grant Nos. 31100672, 51379121 and 61304230), the Shanghai Key Technology Plan Project (Grant Nos. 12510501800, 13510501600).

Biography: WANG Sheng-zheng (1976-), Male, Ph. D.,

Associate Professor