Pressure transient behavior of a slanted well with an impermeable fault*

FENG Guo-qing (冯国庆), LIU Qi-guo (刘启国)

State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China, E-mail: fengguoqing@swpu.edu.cn

Pressure transient behavior of a slanted well with an impermeable fault*

FENG Guo-qing (冯国庆), LIU Qi-guo (刘启国)

State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China, E-mail: fengguoqing@swpu.edu.cn

(Received March 29, 2013, Revised May 8, 2013)

Analytical solution is obtained for the pressure response of a slanted well in a slab reservoir with an impermeable fault. Based on the basic point source solution in an infinite space, the basic point source solution is obtained by using the mirror image principle. Wellbore pressure response of a slanted well is obtained by integration of the basic point source solution along the trajectory of a slanted well and the type curves are computed. The dimensionless bottom hole pressure and type curves are obtained and the sensitivities of related parameters are discussed. The model presented in this paper could be used for the well test analysis of a slanted well in a reservoir bounded by an impermeable fault.

slanted well, point source solution, impermeable fault, type curves

Introduction

In real life, we will have slanted wells when a vertical well penetrates a dipping formation, or when a directionally-drilled well penetrates a horizontal formation. Cinco Ley (1974) first studied the pressure distribution created by a slanted well. The pressure distribution created by a slanted well in a closed boundary rectangular reservoir was established and type curves were also calculated. Simultaneously, the pseudo-skin factor caused by the inclination angle of a slant well was computed.

Abbaszadeh and Peter Hegeman[1]presented analytical solutions for the pressure response of a slanted limited-entry well in an infinite reservoir subject to a pressure support from a gas cap, a bottom water drive, or a combination of both. The method of source and Green’s functions was used to derive the solutions, and averaging the uniform-flux wellbore solutions over the producing interval is shown to yield good approximations to the more exact infinite-conductivity wellbore solutions. Khattab (1991) used the finite element method for calculating the wellbore pressure for a slanted well. The model can be used to compute the wellbore pressure created by a slanted well fully or partially perforated when a cross flow occurs between layers. The sensitivities of the wellbore storage, the skin factor and the anisotropy to the wellbore pressure were also calculated.

Ozkan and Raghavan[2]provided an efficient algorithm to compute the transient pressure responses in inclined wells. The solution was derived in the Laplace domain and cast into computationally efficient forms for all inclination angles. The algorithm allowed the computation of the pressures and the derivatives at the wellbore as well as at observation points. Wang et al.[3]provided an efficient algorithm for the computation of the transient pressure responses of an inclined multi-well system, in which the inclination angle, the changeable production rate, the pattern arrangement, and the number of wells can all be set arbitrarily. The algorithm is verified by example computations. Harmohan et al.[4]presented numerical simulation studies designated to investigate the behavior of horizontal wells and slanted wells that intersect high permeability layers sandwiched between two lower permeability layers.

Li et al.[5]provided a new efficient algorithm for computing transient pressure responses in inclined wells based on the source function and the Newman method which can be used for inclined wells with complex boundaries. Wang et al.[6]presented an efficient algorithm to compute transient pressure distributions caused by slanted wells with arbitrary inclinationin reservoirs.

In addition, Onur[7]provided a technique for determining the formation parameters of spherical and/ or radial flows determined by packer and probe(s) pressure transient measurements in slanted wells for single layer systems. Chang (1989), Besson (1990), Chang (1995) and Chen[8,9]studied the productivity index for slanted wells. Abhijeet[10]studied the pressure transient data of horizontal, slanted and vertical wells in Indian offshore fields. Other scholars such as Avatasmark[11], Zhang et al.[12], Yang et al.[13], Zhang and Liu[14]also studied the pressure transient behavior of slanted wells.

As shown by the previous studies, the calculation of the wellbore pressure for a slanted well is difficult. To our knowledge, little work has been done for the analytical solution in a slab reservoir with an impermeable fault. In this paper, the well test model for a slanted well in a reservoir with an impermeable fault and impermeable top and bottom boundaries is established. The dimensionless bottom hole pressure and type curves are obtained and the sensitivities of related parameters are discussed.

1. The basic point-source solution in an infinite reservoir

For an isotropic reservoir, the flow equation in porous media in spherical coordinates is as follows

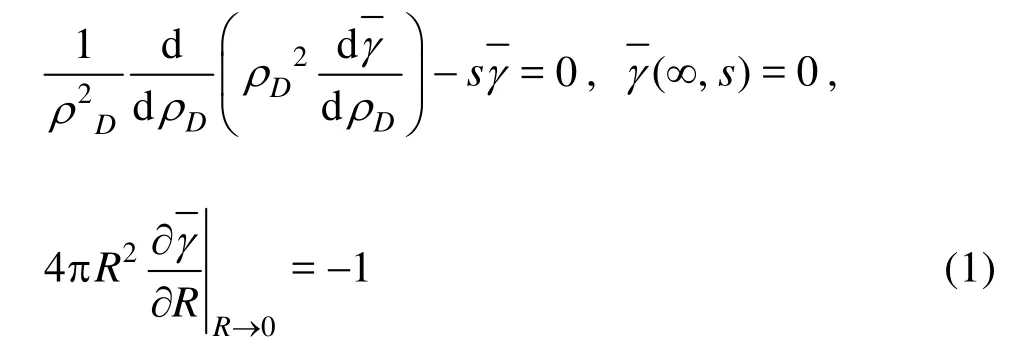
whereρDis the dimensionless distance betweenMDandMD＇,MDis the pressure response at the observation point,MD＇is the point-source,sis the Laplace variable,γis the response of a unit strength source,γisγin the Laplace domain,Ris the radial distance between the point source and the field point.

The general solution of Eq.(1) is

Substituting the boundary condition of Eq.(1) into Eq.(2), the basic solution of the point-source function (Ozkan 1994) is obtained as

Equation (3) is the solution proposed by Lord Kelvin when he studied the heat conduction equation by introducing an instantaneous source, which is the famous solution named the basic solution of Lord Kelvin. The basic point-source solution of different kinds of reservoir models can be obtained by the mirror image principle combined with Eq.(3).

2. The basic solution of instantaneous point-source function in a reservoir with impermeable top and bottom boundaries

The reservoir model with impermeable top and bottom boundaries is shown in Fig.1.

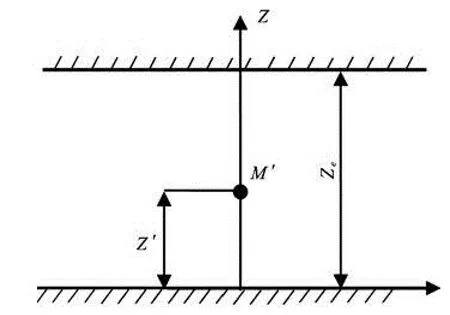
Fig.1 A slab reservoir with impermeable top and bottom boundaries

The instantaneous point-source diffusion equation is

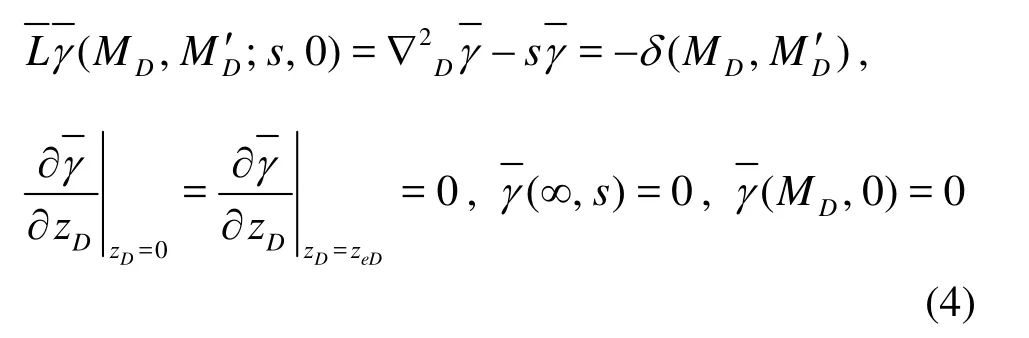
According to the mirror image principle, infinitely many symmetric and equal strength reflections are made along the top and bottom boundaries through the basic solution of Lord Kelvin. The basic solution of the point-source function in a reservoir with impermeable top and bottom boundaries is obtained by the superposition of these point-sources. As shown in Fig.1,M＇ is the position of the point source. The dimensionless distances atz=0 are 2nzeD+zD＇and 2nzeD-zD＇ , respectively, wherenis an integer. Substituting the dimensionless distances in Eq.(3), the basic solution of the point source function in a reservoir with impermeable top and bottom boundaries becomeslis the characteristic length,Lis the Laplace transformation,x,y,zare the space coordinates of the field point in Cartesian coordinates,zeis the reservoir thickness,zeDis the dimensionless reservoir thickness.

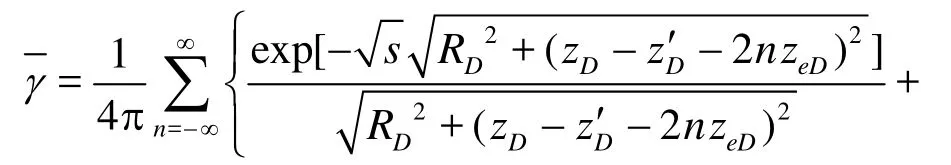
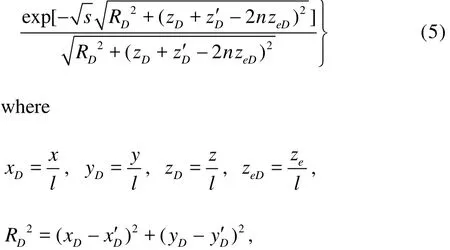
The following is the Poisson formula, which can be used to simplify Eq.(5)

whereξ,ξeare the variables in the Poisson equation,K0is the modified Bessel function of second kind and order zero,tDis the dimensionless time.

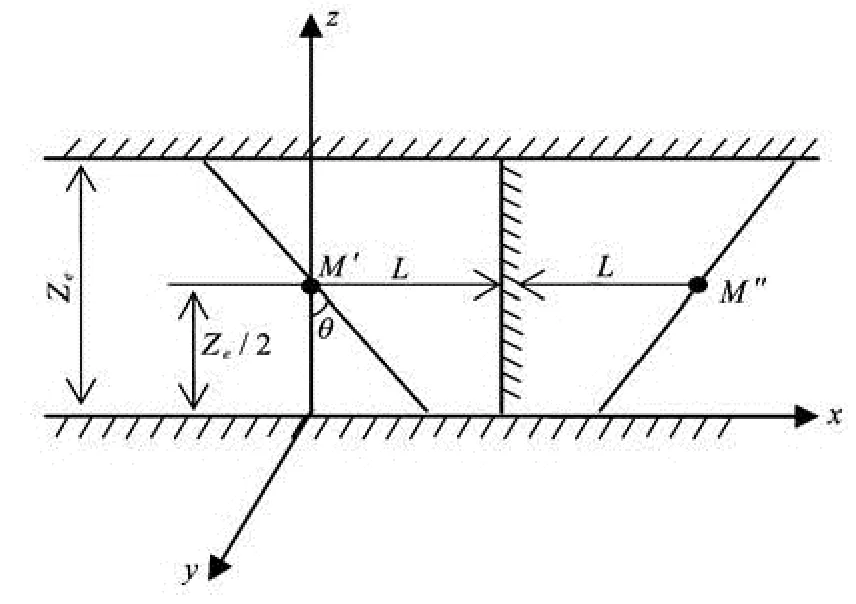
Fig.2 Model of a slanted well in a reservoir bounded with an impermeable fault

3. Wellbore pressure analysis of a slanted well with an impermeable fault

Figure 2 shows the configuration of a slanted well drilled in a slab reservoir under the following conditions:

(1) With an impermeable fault and closed top and bottom boundaries, assumed to be laterally infinite.

(2) The initial reservoir pressurepiis constant, with a uniform thickness ofze.

(3) A single-phase fluid flows from the reservoir to the well at a constant rateq, and the gravity and the capacity pressure effect are ignored.

(4) The oil reservoir is homogeneous and anisotropic.

(5) The length of the well isl.

A model of a slanted well in a reservoir with an impermeable fault and impermeable top and bottom boundaries is shown in Fig.2.

The wellbore pressure can be calculated by the mirror image principle[15]. Supposing that the length between the slanted well’s center and the fault isL, and the fault is impermeable, the mirror image principle is applied to the fault. Now the center of the image well isM＇＇. The basic point-source solution of the model of a slanted well with a fault can be deduced from the basic point-source solution (5) as

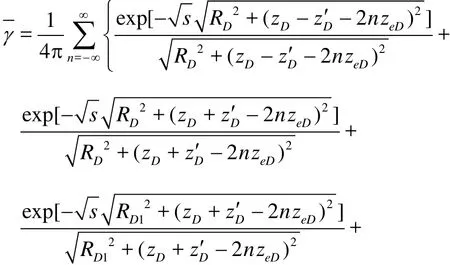
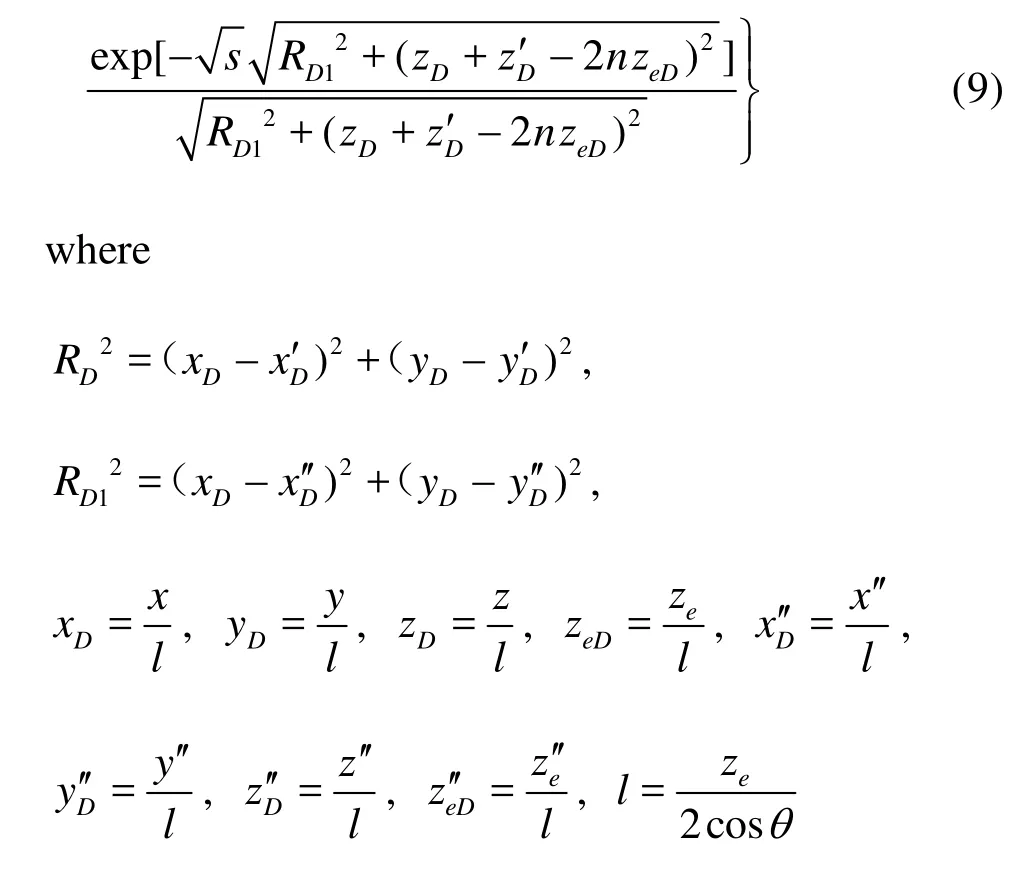
wherexD＇＇,yD＇＇,zD＇＇ are the dimensionless space coordinates of the image well in Cartesian coordinates,θis the inclination angle of the well measured from the vertical axis.

Using the Poisson formula, Eq.(9) can be simplified as

Substituting Eqs.(13), (14) into Eq.(10), and integrating along the trajectory of the slanted well, the dimensionless equation becomes[16,17]

Equation (15) is the well bottom hole pressure response created by a slanted well in a slab reservoir with an impermeable fault and impermeable top and bottom boundaries. Similarly, the well bottom hole pressure of a slanted well in a slab reservoir with an impermeable fault and constant pressure boundaries at the top and bottom can also be solved.

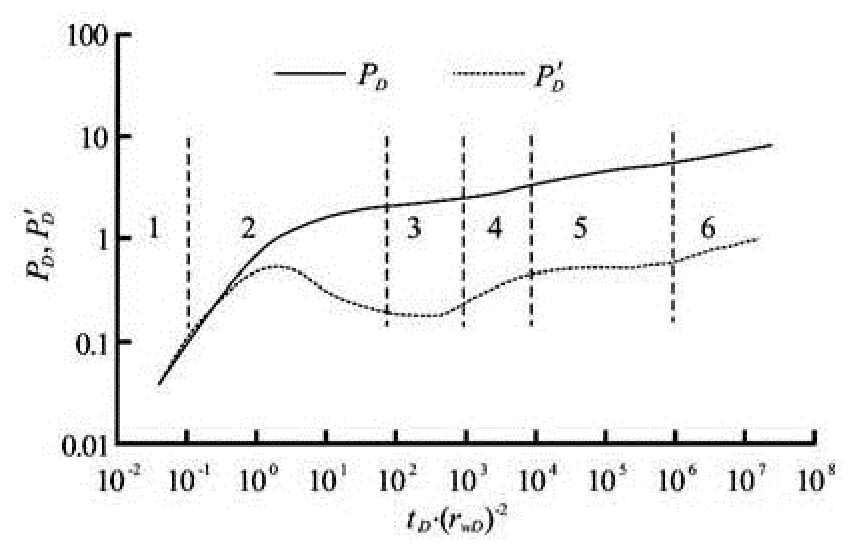
Fig.3 The type curves of a slanted well with an impermeable fault

4. The type curves and analysis

Figure 3 presented the log-log type curves of the dimensionless bottom hole pressure of a slanted well with different inclination angles in a closed boundary slab reservoir with an impermeable fault. As shown in the type curves, the pressure behavior characterization of a slanted well can be divided into six periods: the 1st period, the purely wellbore storage, is characterized by a unit slop in both the pressure and pressurederivative curves, the 2nd period, where the transition period, is dominated by the wellbore storage and the radial flow perpendicular to the well sidewall, the 3rd period, where the radial flow is perpendicular to the well sidewall, which is characterized by a horizontal straight line in the derivative curve and this period is affected by the inclination angle of the slanted well, the 4th period, the transition period, is dominated by the radial flow perpendicular to the sidewall and the intermediate stage radial flow, the 5th period, with the intermediate stage radial flow, which is characterized by the second horizontal straight line in the pressure derivative curve, and the line with the value “0.5”. It reflects the early radial flow in the horizontal direction. The 6th stage is the response of the fault, which is characterized by the horizontal line with the value “1”in the derivative curve.

The inclination angle of a slanted well can affect the shape of the type curve. As shown in Fig.4, with the increase of the inclination angle, the value of the radial flow perpendicular to the well sidewall shown in the pressure derivative curve becomes smaller. When the inclination angle is small enough, the type curve of a slanted well is similar to that of a vertical well. With the increase of the inclination angle, the type curve gradually shows the flow characteristics of horizontal wells.

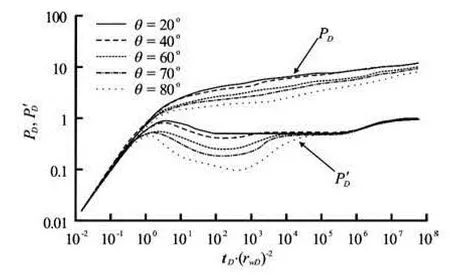
Fig.4 Effect of inclination angle of slanted well on the type curves

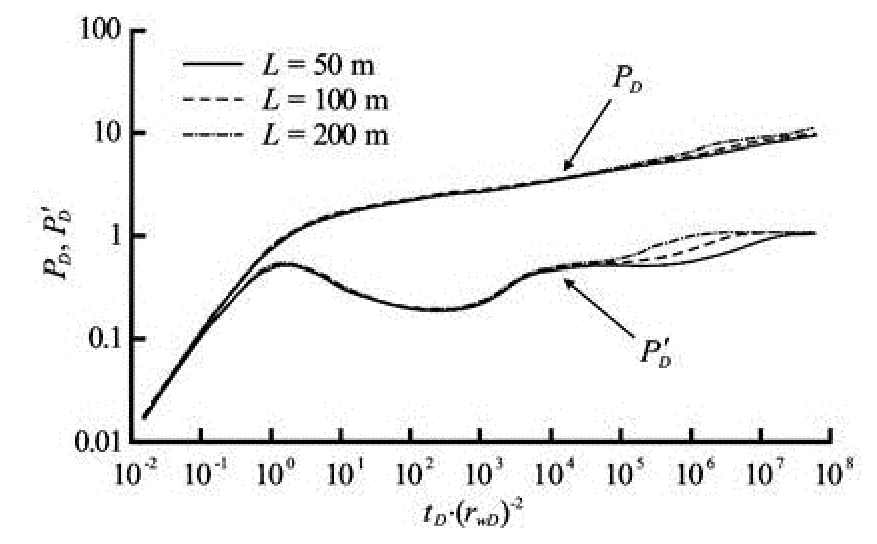
Fig.5 Effect of distance between slanted well’s center and fault on type curves

Figure 5 shows the effect of the distance between the slanted well’s center and the fault on the pressure and pressure derivative curves. The larger the distance between the slanted well’s center and the fault is, the more delayed the response of the fault appears. The reason is that with the increase of the distance between the slanted well’s center and the fault, it will take more time for the impulse of the pressure wave to propagate to the fault. On the other hand, when the distance is small enough, the intermediate stage radial flow in the type curve will not appear.

Figure 6 shows the effect of the wellbore storage constant,CD, on the pressure and pressure derivative curves. The wellbore storage constant has a significant effect on the radial flow perpendicular to the well sidewall. The largerCDis, the bigger the possibility that the early radial flow period perpendicular to the sidewall is masked by the wellbore storage effect.

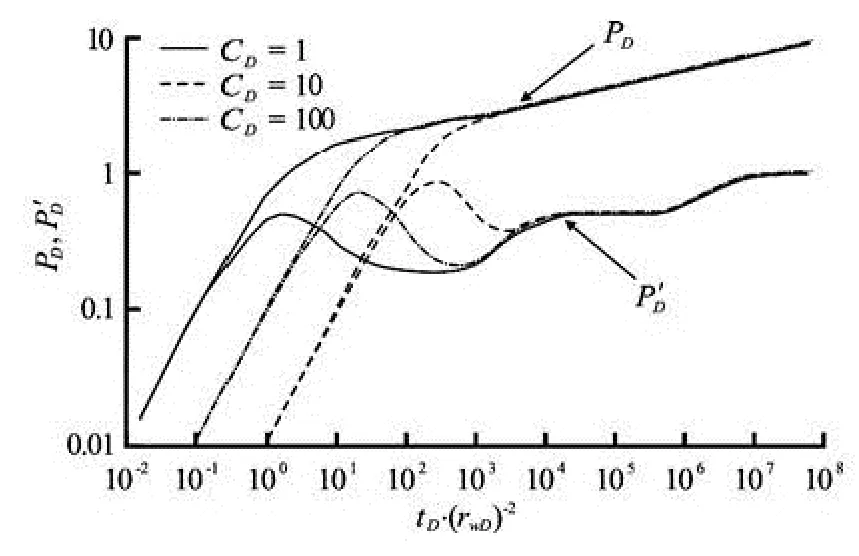
Fig.6 Effect of the wellbore storage constant to type curves

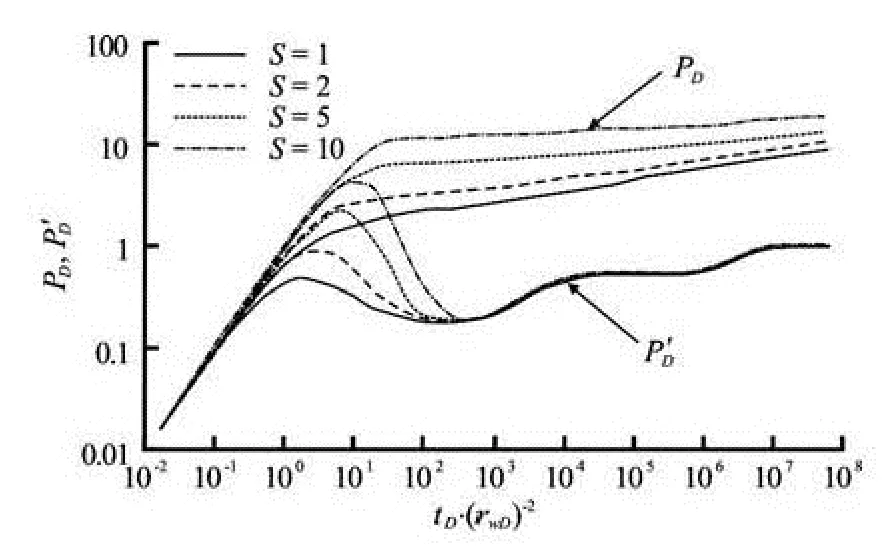
Fig.7 Effect of skin factor to type curves

Figure 7 shows the effect of the skin factor,S, on the pressure and pressure derivative curves. The largerSis, the more obvious the hump in the pressure derivative curve appears and the more delayed the radial flow perpendicular to sidewall becomes.

5. Conclusions

From our study and analysis, the following conclusions are drawn:

(1) The well test model of a slanted well in a slab reservoir with an impermeable fault and impermeable top and bottom boundaries is established, and the solutions are derived by the basic point source in an infinite space combined with the mirror image principle.

(2) The effect of the inclination angle on the pressure behavior for a slanted well is mainly on the 3rd stage in the pressure derivative curve, which is the radial flow perpendicular to the well sidewall. The larger the inclination angle is, the smaller the value of the radial flow perpendicular to the well sidewall is.

(3) The distance between a slanted well’s center and a fault affects the later period in the pressure derivative curve. The pressure derivative curve tends to be a horizontal line of the value 1 in the later period, which is the refection by the impermeable fault boundary. The larger the distance is, the more delayed the flat response of the fault appears.

[1] ABBASZADEH M., PETER HEGEMAN S. Pressuretransient analysis for a slanted well in a reservoir with vertical pressure support[J]. SPE Formation Evaluation, 1990, 5(3): 277-284.

[2] OZKAN E., RAGHAVAN R. A Computationally efficient transient-pressure solution for inclined wells[J]. SPE Reservoir Evaluation and Engineering, 2000, 3(5): 414-425.

[3] WANG De-shan, ZHANG Li and NIE Li-xin et al. A computationally efficient, transient-pressure solution for an inclined multiwell system[J]. Journal of Hydrodynamics, Ser. A, 2005, 20(4): 527-530(in Chinese).

[4] HARMOHAN G., RAYED A. and MOHAMMED B. I. Pressure transient behavior of horizontal and slant wells intersecting a high permeability layer[C]. SPE Middle East Oil and Gas Show and Conference. Bahrain, Kingdom of Bahrain, 2007.

[5] LI Wei, LU De-tang and WANG Lei et al. A transient pressure solution for inclined wells with complex boundaries[J]. Well Testing, 2009, 18(6): 1-5(in Chinese).

[6] WANG Hai-tao, ZHANG Lie-hui and GUO Jing-jing et al. An efficient algorithm to compute transient pressure responses of slanted wells with arbitrary inclination in reservoirs[J]. Petroleum Science, 2012, 9(2): 212-222.

[7] ONUR M., HEGEMAN P. S. and KUCHUK F. J. Pressure-transient analysis of dual packer-probe wireline formation testers in slanted wells[C]. SPE Annual Technical Conference and Exhibition. Houston, Texa, USA, 2004.

[8] CHEN Z., HUAN G. andMA Y. Computational methods for multiphase flows in porous media, in the computational science and engineering Series 2[M]. Philadelphia, USA: Society for Industry and Applied Mathematics Press, 2006.

[9] CHEN Z. Reservoir simulation: Mathematical techniques in oil recovery, in the CBMS-NSF regional conference series in applied mathematics 77[M]. Philadelphia, USA: Society for Industry and Applied Mathematics Press, 2007.

[10] ABHIJEET A. Suitability of horizontal, inclined, and vertical wells on an Indian offshore platform using pressure transient analysis[C]. SPE Annual Technical Conference and Exhibition. San Antonio, Texa, USA, 2012.

[11] AVATASMARK R. A. Klausen: Well index in reservoir simulation for slanted and slightly curved wells in 3D grids[J]. SPE Journal, 2003, 8(1): 41-48.

[12] ZHANG Xiao-long., LI Xiao-ping and ZHANG Xu et al. Research on inclined well test model for orthographic fault slabby double porosity reservoir[J]. Well Testing, 2012, 21(6): 1-4(in Chinese).

[13] YANG lei, HUANG Cheng and DUAN Yong-gang et al. Pressure transient interpretation of inclined well and lateral well[J]. Journal of Southwest Petroleum Institu- te, 2002, 24(2): 25-27(in Chinese).

[14] ZHANG Xu, LIU Qi-guo. Research on inclined well test model for slabby fault reservoir[J]. Natural gas and oil, 2012, 30(5): 60-62(in Chinese).

[15] RUBIN R. L. Duhamel solutions of non-homogeneous analogue wave equations[J]. Proceedings of the American Mathematical Society, 2007, 135(3): 777- 785.

[16] UMAROV S. R., SAIDAMATOV E. M. A generalization of Duhamel’s principle for differential equations of fractional order[J]. Doklady Mathematics, 2007, 75(1): 94-96.

[17] DOMINIC G. Analytical solution to the unsteady onedimensional conduction problem with two time-varying boundary conditions: Duhamel’s theorem and separation of variables[J]. Heat and mass transfer, 2010, 46(7): 707-716.

10.1016/S1001-6058(14)60108-6

* Biography: FENG Guo-qing (1974-), Male, Ph. D., Associate professor