电力系统暂态稳定最小负荷裕度的计算方法

常乃超，陶洪铸，郭建成，辛耀中

(国家电网公司，北京100032)

电力系统暂态稳定最小负荷裕度的计算方法

常乃超，陶洪铸，郭建成，辛耀中

(国家电网公司，北京100032)

为考虑不同的负荷—发电增长方向对电力系统暂态稳定负荷裕度的影响，提出了计算电力系统暂态稳定最小负荷裕度的最优化模型。该模型使用改进PEBS法提供的暂态稳定量化指标构成稳定约束条件，具有与暂态时域仿真相同的模型适应性。根据点到曲面最短距离的基本定理，给出了求解所提出最优化模型的数值方法。该方法的基本思想是以暂态稳定临界点处暂态稳定边界曲面的法向量作为求解迭代过程中的负荷—发电增长方向，反复迭代求出暂态稳定最小负荷裕度。理论上，该模型不但可以计算各种发电—负荷增长方向上的暂态稳定最小负荷裕度，也可用于计算暂态稳定最大负荷裕度。所提出的计算电力系统暂态稳定最小负荷裕度的最优化模型及其求解方法可以考虑各种系统运行参数的约束。数值算例验证了所提出的模型及求解方法。

暂态稳定;负荷裕度;电力系统

1 引言

在线稳定分析及预警系统已成为智能电网调度技术支持系统的重要应用。目前，在线稳定分析及预警系统的主要功能是在给定的故障及过渡方案(即任意系统运行参数的变化方向，通常是考察负荷—发电增长)下，逐步恶化系统运行方式，找到系统的稳定极限，给出系统的稳定裕度［1-8］。显然，这样得到的稳定裕度依赖于选取的过渡方案，以负荷—发电增长方向为例，不同的负荷—发电增长方向下得到的负荷功率裕度相差可能很大。为了给调度运行人员提供更为全面深入的系统稳定裕度信息，本文探讨如何求取最小负荷裕度的问题。最小负荷裕度是各种可能的负荷—发电增长方向上负荷裕度的最小值。以暂态稳定负荷裕度为例，某个故障下最小负荷裕度的意义是只要负荷增加量小于此负荷裕度，则无论所增加的负荷在各负荷母线上如何分配，系统都是暂态稳定的。

本文提出了计算暂态稳定约束下最小负荷裕度的最优化模型，并根据点到曲面最短距离的基本定理，给出了求解该模型的数值方法。求解方法的基本过程是给定初始负荷—发电增长方向后，求出该增长方向上的暂态稳定临界点(位于注入空间中暂态稳定边界曲面上)，以该临界点处注入空间中暂态稳定边界曲面的法向量作为下一次计算的负荷—发电增长方向，如此反复迭代，直至当前运行点与暂态稳定临界点之间连线矢量的方向与暂态稳定临界点处暂态稳定边界曲面法向量的方向相同。

2 暂态稳定最小负荷裕度的最优化模型

为求出暂态稳定限制下的最小负荷裕度，构造如下最优化模型:

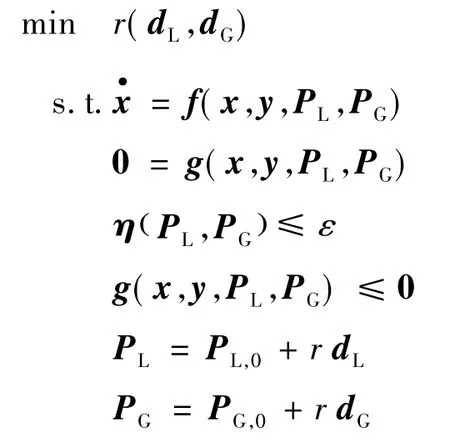
其中，x、y分别为电力系统暂态过程状态变量和代数变量;f(·)、g(·)为描述暂态过程的微分代数方程;PL∈Rm为负荷注入向量;PG∈Rn为发电注入向量;PL，0为当前运行点负荷注入向量;PG，0为当前运行点发电注入向量;η(PL，PG)为暂态稳定量化指标;ε为暂态稳定裕度门槛值;g(·)≤0为运行约束;r∈R为负荷裕度;为负荷增长方向向量;为发电增长方向向量;=1。

暂态稳定约束下的最小负荷裕度r*表示不论负荷增量在各负荷母线上如何分配，系统至少能够承受总和为r*的负荷增量而不发生暂态失稳。

3 求解方法

3.1 暂态稳定量化指标

电力系统暂态稳定量化指标η表征了系统运行点与暂态安全域边界的接近程度，η接近于零意味着系统接近暂态不稳定。目前，已有很多能够提供暂态稳定量化指标的分析方法，例如BCU、PEBS、Hybrid Method、EEAC、半 张 量 积 等 方法［8-15］。这里选择改进PEBS方法提供的暂态稳定量化指标［12］。

改进PEBS方法的基本思想是基于时域仿真得到的系统受扰轨迹，结合PEBS方法的基本思想提取暂态稳定量化指标，综合了时域仿真法及PEBS方法的优点，能够考虑各种复杂的系统模型且不需要计算故障后的不稳定平衡点。

惯性中心坐标下多机系统转子摇摆方程为

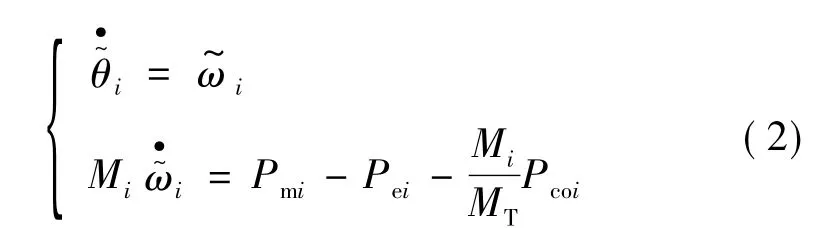
惯性中心坐标系定义为

其中，δi、ωi、Pmis、Pei、Mi分别为第i台发电机的转子角度、角速度、输入机械功率、输出电磁功率、转子惯量。

改进PEBS方法中系统的能量函数定义为

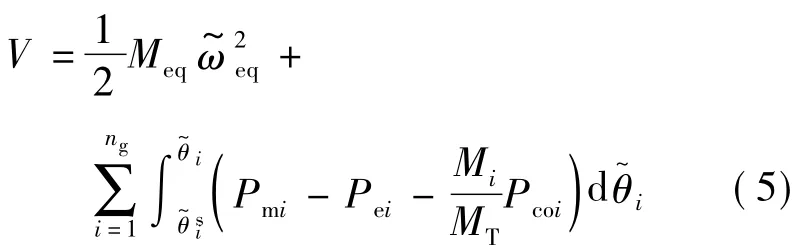
对于暂态不稳定情形，改进PEBS方法提供的稳定量化指标为

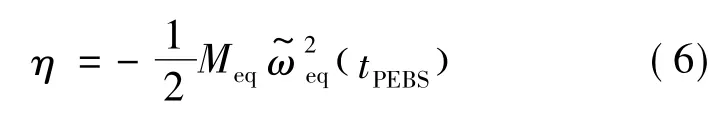
式中，tPEBS表示系统轨迹穿越PEBS的时刻。

对于暂态稳定情形，改进PEBS方法提供的稳定量化指标为

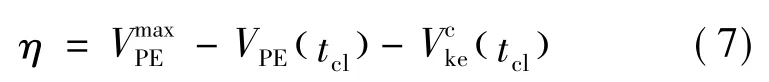
其中，tcl为故障切除时刻;分别为故障切除时刻的势能、动能;为持续故障下的势能最大值。所谓持续故障是指，在时刻tins(tins＞tcl)重新插入故障势能所能达到的最大值。tins满足

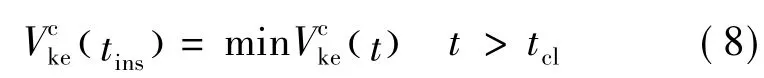
3.2 求解过程

注入空间中系统的暂态稳定边界曲面方程为

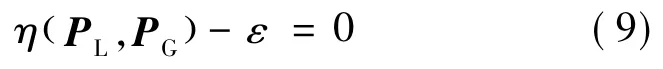
假定当前运行点 (PL0，PG0)与曲面上的点之间的连线长度为当前运行点(PL0，PG0)到暂态稳定边界曲面的最短距离，则根据点到曲面距离的基本定理，点(PL0，P)G0与点之间连线的方向必与暂态稳定边界曲面在点处的法向量方向重合。暂态稳定边界曲面在点处的法向量为

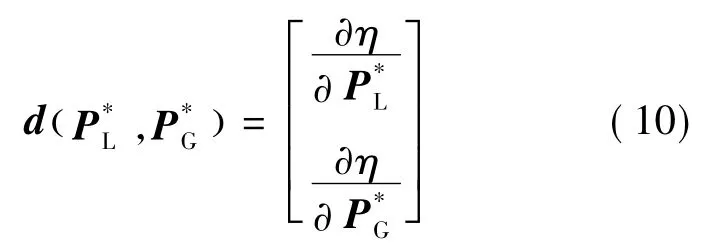
基于暂态稳定边界曲面的法向量，可构造如下求解过程:

(1)置k=0;

(2)给定负荷及发电增长方向dL(k)，dG(k)，在该方向上以一定步长h逐步增加负荷及发电，即PL=PL0+mh dL，PG=PG0+mh dG，m=1，2，…，Nk，当m=Nk时系统暂态失稳。dL(k)，dG(k)方向上的负荷裕度为r(k)=Nkh，暂态稳定边界曲面上的临界点为，其中;

(4)将负荷及发电增长方向修正为

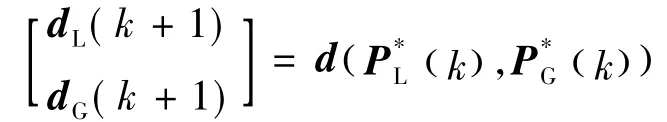
并归一化

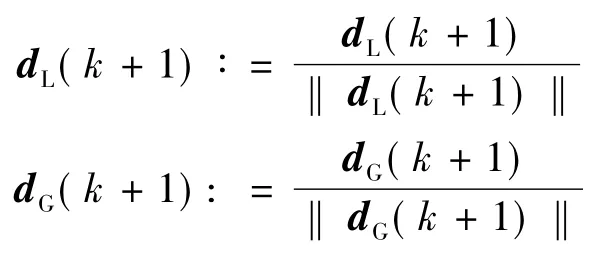
(5)置k∶=k+1，返回第(2)步。

4 数值仿真

数值仿真采用如图1所示的5机两区域系统［16］。发电机均采用6阶模型，每台发电机均配有简单的比例励磁控制器和PSS模型，母线1、2、12、22上的发电机配有简化的调速器模型，发电机1设为平衡机。母线4、14上的负荷采用恒阻抗模型，母线21上的负荷采用恒阻抗和电动机组合模型，其中电动机模型负荷占40%。基准功率为100MVA，以下功率均为标幺值，表1给出了初始发电和负荷分布。

图1 两区域系统Fig．1 Two area power system

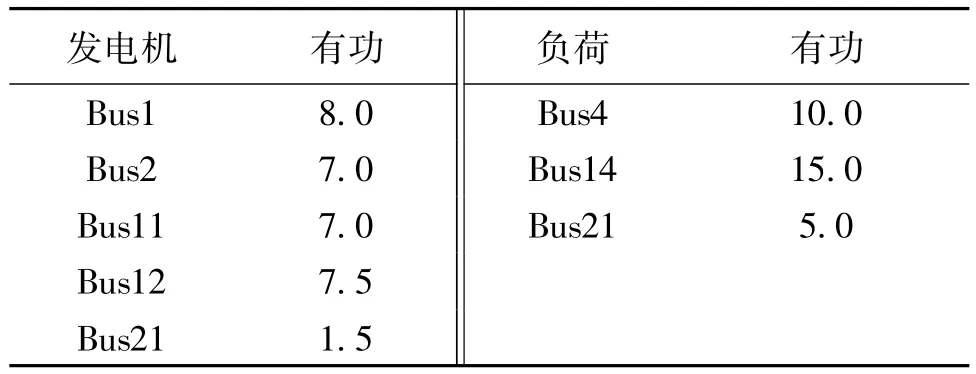
表1 发电和负荷初始分布(pu)Tab．1 Initial distribution of generation and load(pu)

负荷及发电的初始增长方向为按比例增长dL= ［0.3333，0.5，0.1667］T， dG= ［0.3043，0.3043，0.3261，0.0652］T。所考察的故障为0.1s时线路3-25在母线25侧发生三相短路，0.15s时母线25侧开关跳开，0.2s时母线3侧开关跳开。初始发电和负荷状态下各发电机相对于母线1上的发电机的转子角度曲线如图2所示。

沿负荷及发电初始增长方向按照rstep=0.05的步长增加负荷和发电，当r=2.7时，系统处于临界稳定状态，响应如图3所示。

按照3.2节给出的求解过程进行计算，迭代8次后收敛，最终的负荷及发电增长方向为 dL= ［0.0564，0.0806，0.863］T，dG=［0.0546，0.0546，0.0526，0.8381］T，暂态稳定最小负荷功率裕度r=1.09，即最小负荷裕度为109MW。这意味着无论所增加的109MW负荷是以何种比例分配到各个负荷节点上，所增加的109MW负荷由哪些发电机承担，系统都是暂态稳定的。所得到的最小负荷裕度可作为暂态稳定监控的重要指标。另外，可以看到，由于负荷21、发电机22离故障地点距离较近，因此其负荷和发电的增长对暂态稳定影响较大，表现在最终的负荷及发电增长方向中负荷21、发电机22对应的比例较大。为验证所得到的最小负荷裕度，将118MW全部加在负荷21及发电机22上，仿真表明系统暂态稳定，如图4所示。

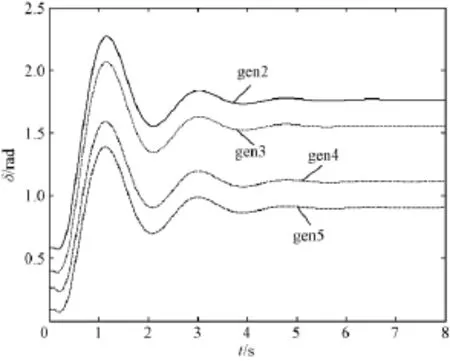
图2 初始状态下的发电机转子角度响应Fig．2 Generator angle response at initial state

图3 初始增长方向下r=2.7时的角度响应Fig．3 Generator angle response under initial increasing direction(r=2.7)

5 结论

本文提出了计算电力系统暂态稳定最小负荷裕度的最优化模型，该模型中的暂态稳定约束量化指标由改进PEBS方法给出，具有与时域仿真方法相同的模型适应性，可以考虑系统复杂动态模型。

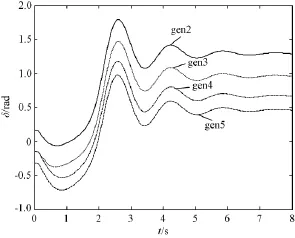
图4 负荷21及发电机增加109MW时的角度响应Fig．4 Generator angle response when load 21 and generation 22 increasing 109MW

选定某个负荷及发电初始增长方向后，逐步增加负荷及发电得到该方向上的最小负荷裕度及暂态稳定边界曲面上的临界稳定点，计算该点处暂态稳定边界曲面的法向量，并将该法向量归一化后作为下一次迭代的负荷及发电增长方向，反复迭代得到最小负荷功率裕度。数值算例表明，所提出的模型及求解方法是有效的。本文提出的电力系统暂态稳定最小负荷裕度实际上还可看作注入空间中电力系统暂态稳定域的最短半径。

电力系统暂态稳定最小负荷裕度应该成为在线稳定分析及预警系统的一个重要监视指标，对于调度员掌握电力系统实时运行工况稳定性的深层信息具有重要作用，有利于避免对特殊运行方式下系统稳定裕度的误判。如何减少最小负荷裕度指标的保守性是一个值得进一步研究的课题，例如，可根据超短期负荷预测结果将负荷增长方向限制在一定范围之内进行寻优，从而得到更贴近实际运行经验的负荷裕度指标。

［1］Vittal V．Consequence and impact of electric utility industry restructuring on transient stability and small-signal stability analysis［J］．Proceedings of IEEE，2000，88 (2):196-207．

［2］Wu F F，Kumagai S．Steady-state security regions of power systems［J］．IEEE Transactions on Circuits and Systems，1982，29(11):703-711．

［3］Wu F F，Tsai Y-K，Yu Y．Probabilistic dynamic security assessment of power systems，Part I:Basic model［J］．IEEE Transactions on Circuits and Systems，1983，30 (3):148-159．

［4］Kaye R J，Wu F F．Dynamic security regions for power systems［J］．IEEE Transactions on Circuits and Systems，1982，29(9):612-623．

［5］Kundur P．Power system stability and control［M］．New York，USA:MacGraw-Hill，1993．

［6］倪以信，陈寿孙，张宝霖 (Ni Yixin，Chen Shousun，Zhang Baolin)．动态电力系统的理论和分析 (Theory and analysis of dynamic power systems)［M］．北京:清华大学出版社 (Beijing:Tsinghua University Press)，2002．

［7］Vittal V，Zhou E Z，Hwang C，et al．Derivation of stability limits using analytical sensitivity of the transient energy margin［J］．IEEE Transactions on Power Systems，1989，4(4):1363-1372．

［8］Chiang H D，Wu F F，Varaiya P P．A BCU method for direct analysis of power system transient stability［J］．IEEE Transactions on Power Systems，1994，9(3): 1194-1208．

［9］Chiang H D，Wu F F，Varaiya P P．Foundations of the potential energy boundary surface method for power system transient stability analysis［J］．IEEE Transactions on Circuits and Systems，1988，35(6):160-172．

［10］Sauer P W，Behera A K，Pai M A，et al．Trajectory approximations for direct energy methods that use sustained faults with detailed power system models［J］．IEEE Transactions on Power Systems，1989，4(2):499-506．

［11］Maria G A，Tang C，Kim J．Hybrid transient stability analysis［J］．IEEE Transactions on Power Systems，1990，5(2):384-391．

［12］Tang C，Graham C E，El-Kady M，et al．Transient stability index from conventional time domain simulation ［J］．IEEE Transactions on Power Systems，1994，(3): 1524-1530．

［13］Fouad A A，Kruempel K C，Vittal V，et al．Transient stability program output analysis［J］．IEEE Transactions on Power Systems，1986，1(1):2-9．

［14］Haque M H．Hybrid method of determining the transient stability margin of a power system［J］．IEE Proc．-Gener．Transm．Distrib．，1996，143(1):27-32．

［15］梅生伟，刘锋，薛安成 (Mei Shengwei，Liu Feng，Xue Ancheng)．电力系统暂态分析中的半张量积方法(The semi-tensor product method for power systems transient stability analysis) ［M］．北京:清华大学出版社(Beijing:Tsinghua University Press)，2010．

［16］Power System Toolbox(PST)［EB/OL］．http://www．ecse．rpi．edu/pst/Downloads．html．

Method for calculating minimal load margin constrained by power system transient stability

CHANG Nai-chao，TAO Hong-zhu，GUO Jian-cheng，XIN Yao-zhong (State Grid Corporation of China，Beijing 100032，China)

In order to consider the effect of different load-generation increasing directions to the load margin constrained by power system transient stability，an optimization model for calculating the minimal load margin constrained by power system transient stability is proposed．The stability quantitative index proposed by the improved PEBS method is used to construct the transient stability constraint，and it has the same model adaptation as the time domain transient simulation method．A numerical method for solving the proposed optimization model is given out based on the basic theorem about the distance from a point to a curved surface．The basic idea of the proposed solution method is that the normal vector at the critical point of the power systems transient stability boundary surface is taken as the load-generation increasing direction in the iterative solution procedure，and the minimal load margin constrained by power systems transient stability is finally acquired．Theoretically，the proposed model and method can also be applied to calculating the maximal load margin constrained by power system transient stability，and all kinds of power system operating constraints can also be considered．A numerical example verifies the proposed model and method．

transient stability;load margin;power systems

TM712

A

1003-3076(2014)06-0047-05

2013-07-13

国家高技术研究发展计划(863计划)研究资助项目(2011AA05A118)

常乃超(1977-)，男，河南籍，高级工程师，博士，研究方向为电力系统分析与调度自动化;陶洪铸(1973-)，男，安徽籍，高级工程师，硕士，研究方向为电网调度自动化。