基于改进PSO的Terminal分段滑模励磁控制器设计
2014-06-01张虹,于雷,徐滨
张 虹,于 雷,徐 滨
(东北电力大学电气工程学院,吉林省吉林市132012)
基于改进PSO的Terminal分段滑模励磁控制器设计
张 虹,于 雷,徐 滨
(东北电力大学电气工程学院,吉林省吉林市132012)
为获得较好的收敛速度,在快速终端滑模面的基础上,设计了一种Terminal分段滑模励磁控制方法。滑模控制律中参数较多,利用粒子群算法(PSO)较好的搜索能力对控制律参数进行寻优。利用单机无穷大系统,进行了多种扰动下的仿真分析。仿真结果表明,本文所采用的控制策略,响应速度较快,能够有效地提高系统的静态和暂态稳定性,控制精度较高。
Terminal分段滑模控制;粒子群算法;励磁控制;单机无穷大系统
1 引言
同步发电机励磁控制方式从早期的电力系统稳定器(PSS)、最优励磁控制器(LOEC)等线性化控制方式,发展为非线性多变量控制方式。基于先进的非线性控制理论的励磁控制有助于提高电力系统的稳定性[1,6]。20世纪70年代中期开始用于励磁系统中的变结构控制[2],其滑动模态与对象参数及干扰无关,较好地提高了系统的鲁棒性。
Terminal滑模控制是变结构控制方法的一种典型代表,它在滑动超平面的设计中引入了非线性函数,滑模面与系统到达平衡状态的收敛时间有关。因而,可以在系统不同的趋近过程中分别设计合适的滑模面,以进一步提高整体的收敛速度[3-5]。本文在快速终端滑模面上,根据系统跟踪误差的大小,设计了一种Terminal分段滑模励磁控制器,并利用粒子群算法简单、搜索速度快等特点,优化控制器的设计参数。利用典型单机无穷大系统进行了仿真研究,从而验证了所提控制策略的有效性和可行性。
2 Terminal滑模励磁控制器设计
2.1 单机励磁系统的数学模型
图1所示为典型的带有励磁控制的单机无穷大系统,发电机G经过主变压器、输电线路联接到无穷大系统。

图1 单机无穷大系统模型Fig.1 Single machine infinite-bus system model
若忽略变压器输电线路电阻上的有功功率损耗,假设发电机机械功率不变,可列写出具有励磁控制的单机无穷大输电系统的三阶状态方程[6]:
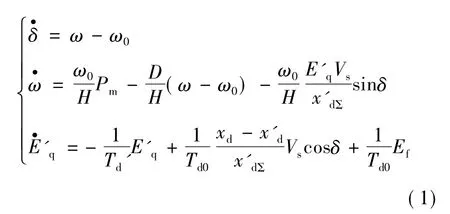
其中,T'd=Td0x'dΣ/xdΣ;Ef为发电机励磁电压,即输入的控制量。通过坐标变换,令

以此可得到一个完全可控的线性系统,即Brunovsky标准型:

2.2 Terminal分段滑模励磁控制器的设计
Terminal滑模控制是对普通滑模控制方法的改进,在滑模面上跟踪误差能够在有限时间内收敛到零,其中,全局快速Terminal滑模控制结合了线性滑模和快速Terminal滑模的优点,具有良好的全过程收敛特性,且收敛速度快,其典型滑模面可表示为[7]:

式中,α、β>0,p>q且为正奇数。
由式(5)得,在其滑动模态下:

对式(6)积分可得系统从任意状态收敛到滑动模态的时间为:

收敛时间与α、β、p、q有关,给定适当值可使系统在有限时间内收敛。式(6)表达了状态量x的收敛速度,当系统状态x远离平衡点时,线性滑模面-αx的速度比快速Terminal滑模面快;当系统状态x在平衡点附近时,快速Terminal滑模面 -βxq/p的收敛速度优于线性滑模面。
考虑到不同趋近阶段各自的收敛特性,将滑模面分为两段,每段均具有全局的收敛特性:

式中,p、q、m和n为正奇数,且p>q,m>n。
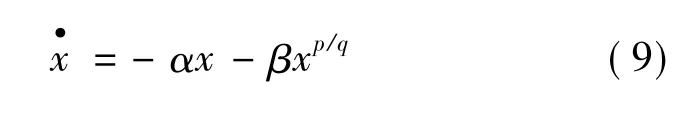

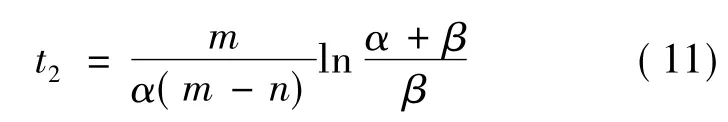
则系统到达平衡状态的总时间为:

图2为简单二阶SISO系统的状态量变化曲线,参数和初始值相同,可以看出应用Terminal分段滑模面时,系统的收敛速度高于全局快速Terminal滑模面,从初始状态到达平衡态的过程中,缩短了收敛时间,改善了趋近效果。
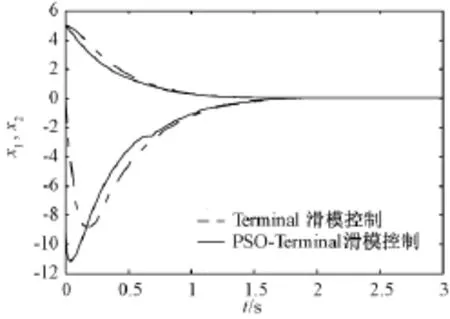
图2 两种滑模面下系统状态量的变化曲线Fig.2 Response curves of state variables of two kinds of SM surface
设计滑模面为:

设计励磁控制率为:

式中,αi>0;βi>0;pi、qi、p、q、mi、ni、m、n为正奇数(i=0、1)。
证明此分段滑模控制系统的稳定性。

由式(16)~式(18)得:

构造Lyapunov函数:

则有:
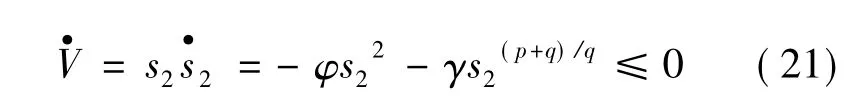

故系统具有李雅普诺夫稳定性。
3 改进的粒子群优化算法
粒子群算法的基本思想是随机初始化一群没有体积没有质量的粒子,每个粒子代表一个优化问题的可行解,粒子在解空间中以一定的速度飞行,根据自身的历史信息和群体信息调整飞行的速度和方向,以迭代的方式搜索最优解。
设一个d维的搜索空间里有M个粒子,该群体以一定的速度飞行。粒子i的位置可以表示为xi= (xi1,xi2,...,xid),xid∈[Ld,Ud],Ld、Ud为搜索空间的下限和上限;粒子i的速度vid∈[vmin,d,vmax,d],vmin,d、vmax,d为最小和最大速度;该粒子迄今为止搜索到的最优位置pi=(pi1,pi2,...,pid);整个粒子群迄今为止搜索到的最优位置pg=(pg1,pg2,...,pgd)。考虑到协调PSO算法的全局和局部寻优能力,在每次迭代中,粒子更新速度和位置:
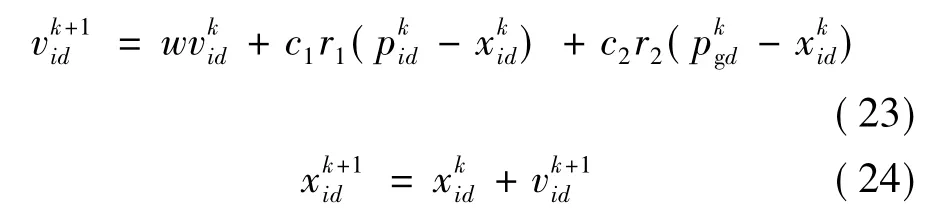
惯性权重w的值决定了粒子前一时刻对当前速度的影响程度,故可调整其值来提高寻优能力。采用线性递减计算公式[8]:

其中,r1、r2为均匀分布在(0,1)区间随机数; maxgen为最大迭代次数;i为当前迭代次数。
为了获取满意的过渡过程动态特性,本文将目标函数进行了改进,将误差绝对值时间积分性能指标作为参数选择的最小目标函数,并在目标函数中加入控制输入的平方项:

式中,e(t)为系统误差;u(t)为控制器的输出;ω1=0.999;ω2=0.001。改进粒子群算法的流程图如图3所示。

图3 改进PSO算法流程图Fig.3 Flow chart of improved PSO
4 基于改进PSO算法的Terminal分段滑模励磁控制器设计
上述的Terminal分段滑模控制中,选取适当的参数值可使系统在整个收敛过程都具有较快的收敛速度。对于参数的选择,与改进的粒子群优化算法相结合,通过迭代寻优找到控制率的最佳参数,达到最好的控制效果。
4.1 PSO-Terminal滑模控制仿真结果与分析
本文将传统的Terminal滑模励磁控制方法与PSO-Terminal滑模控制策略对比,针对于单机无穷大系统中发生的小扰动,将优化后的控制策略应用到三相短路的大扰动控制系统中,利用Matlab进行仿真分析。典型单机无穷大系统参数为:ω0= 100πrad/s,H=7s,D=8pu,Pm=0.9 pu,Vs= 1pu,xd=1.8pu,x'd=0.3,xdΣ=2.2,x'dΣ=0.7,Td0=8s,xq=1.8,xqΣ=2.2。设置小干扰为t=0s时,发电机功角偏离平衡点Δδ=-5°,给定系统初始值为(δ,ω,E'q)=(40,314,1.002);设置大干扰为t=2s时系统发生三相短路故障,0.1s后故障消失。在优化过程中,取粒子种群数为30,迭代次数为40次,wmax=0.9,wmin=0.4,c1=c2=2。考虑到pi、qi、p、q、mi、ni、m、n的取值,在初始化和更新时取为正奇数。
经优化后的参数与未优化的传统Terminal控制方法[9]的参数如表1和表2所示;以式(26)为目标函数得到的适应度值变化曲线如图4所示,并与经典PSO算法来对比。可知,对于改进目标函数的粒子群算法,在传统PSO算法收敛时仍能继续进化,收敛速度更快,控制效果更好。

表1 |s0|≥1时两种方法中滑模面的各参数值Tab.1 Parameter values of two SM surfaces as|s0|≥1

表2 |s0|<1时两种方法中滑模面的各参数值Tab.2 Parameter values of two SM surfaces as|s0|<1

图4 适应度值Fig.4 Fitness value
4.2 静态稳定性分析
研究PSO-Terminal滑模控制策略在小干扰下的控制效果,与传统全局快速Terminal滑模控制方法进行对比来分析其静态稳定性。本方法在设计工程中采用了分段滑模面,利用粒子群算法优化参数,使控制器达到最佳控制效果。图5是发电机机端电压在小扰动下的响应,结合图6所示的发电机功角响应曲线,可以看出系统功角在远离平衡态时具有更快的收敛速度,此时机端电压亦能快速收敛;在平衡态附近功角和机端电压能够快速恢复到稳态值,波动幅值较小,保证了系统的静态稳定。
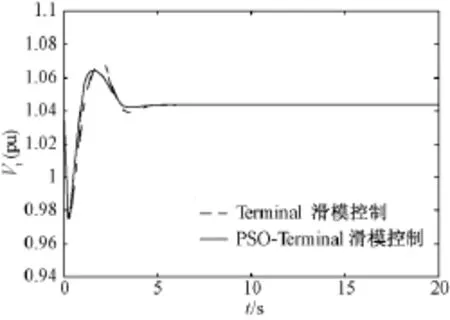
图5 发电机端电压响应曲线Fig.5 Response curve of terminal voltage
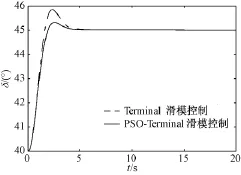
图6 发电机功角响应曲线Fig.6 Response curve of generator power angle
图7给出了发电机角速度的响应曲线,可知PSO-Terminal滑模控制的效果优于全局快速Terminal滑模控制,超调量明显减小。在小干扰下,通过粒子群算法对控制律在两种滑模面下的12个参数寻优,能够有效地抑制振荡,增加了系统的静态稳定性。
4.3 暂态稳定性分析
图8和图9所示为三相短路故障下的响应过程,可以看出PSO-Terminal分段滑模控制能够使发电机机端电压和功角在短时间内达到稳定,有效地抑制了系统振荡,改善了系统暂态稳定性的能力。这两种控制方法都具有扰动后维持机端电压稳定的能力,但是在大扰动过程中,改进的PSO-Terminal分段滑模控制效果要优于全局快速Terminal滑模控制方法[10]。
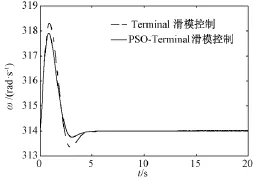
图7 发电机角速度响应曲线Fig.7 Response curve of generator angular velocity

图8 机端电压动态响应Fig.8 Dynamic response curve of terminal voltage

图9 发电机功角动态响应Fig.9 Dynamic response curve of generator power angle
5 结论
本文将改进的粒子群算法与Terminal分段滑模控制相结合,应用于发电机励磁控制器的设计。根据滑动模态的收敛时间特性,提出了Terminal分段滑模面,针对收敛过程的差异分别设计了滑模控制策略。利用PSO算法优化参数,综合考虑励磁系统的控制性能,在目标函数中加入控制输入的平方项,并进行静态与暂态稳定性的分析,验证了本文所采用方法具有较好的稳定性和鲁棒性。
[1]马幼捷,王新志,周雪松 (Ma Youjie,Wang Xinzhi,Zhou Xuesong).基于微分几何理论和自抗扰控制技术的励磁控制器设计 (Excitation control design based on differential geometry theory and active disturbance rejection control)[J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy),2007,26(1):34-37.
[2]王兴贵,黄忠良 (Wang Xinggui,Huang Zhongliang).同步发电机励磁系统的智能变结构控制 (Intelligent sliding mode variable structure control for synchronous generator excitation system)[J].电力系统及其自动化学报 (Proceedings of the CSU-EPSA),2006,18(6): 79-82.
[3]Abido M A,Abdel-Magid Y L.Hybridizing rule-based power system stabilizers with genetic algorithms[J].IEEE Transactions on Power Systems,1999,14(2): 600-607.
[4]Man Z H,Palan I.Decentralized three segment nonlinear sliding mode control for robotic manipulators[A].IEEE International Workshop on Emerging Technologies and Factory Automation[C].Cairns,Australia,1992.607-612.
[5]Wang Wei-yen,Leu Yih-guang,Lee Tsu-tian.Robust adaptive controller design for a class of uncertain nonlinear systems using online T-S fuzzy-neural modeling approach [J].IEEE Transactions on Cybernetics Systems,2011,41(2):542-552.
[6]卢强,梅生伟,孙元章 (Lu Qiang,Mei Shengwei,Sun Yuanzhang).电力系统非线性控制 (Nonlinear control for power systems)[M].2版 (Second Edition).北京:清华大学出版社 (Beijing:Tsinghua University Press),2008.
[7]刘金琨 (Liu Jinkun).滑模变结构控制Matlab仿真(Matlab simulation for sliding mode control)[M].北京:清华大学出版社 (Beijing:Tsinghua University Press),2005.
[8]李丽,牛奔 (Li Li,Niu Ben).粒子群优化算法 (Particle swarm optimization)[M].北京:冶金工业出版社 (Beijing:Metallurgical Industry Press),2009.
[9]Yu Shuanghe,Yu Xinghuo,Man Zhihong.Robust global terminal sliding mode control of SISO nonlinear uncertain systems[A].Proc.of the 39th IEEE Conference on Decision and Control[C].Sydney,Australia,2000.2198-2203.
(,cont.on p.35)(,cont.from p.22)
[10]曾正,刘涤尘,廖清芬,等 (Zeng Zheng,Liu Dichen,Liao Qingfen,et al.).Terminal滑模变结构励磁控制设计及仿真研究(Design and simulation study on terminal sliding mode variable structure excitation control) [J].电力系统保护与控制 (Power System Protection and Control),2010,38(23):1-5.
Design of Terminal piecewise sliding mode excitation controller based on improved PSO
ZHANG Hong,YU Lei,XU Bin
(College of Electrical Engineering,Northeast Dianli University,Jilin 132012,China)
In order to obtain better convergence rate,Terminal piecewise sliding mode excitation control is designed based on fast terminal sliding mode surface.Sliding mode control strategy contains more parameters,so that to solve this problem,particle swarm optimization(PSO)is used to optimize the parameters for the preferable ability of searching.The simulation and analysis are done under a variety of disturbance based on single machine to infinitebus system.The simulation results show that the response rate of the control strategy proposed in this paper is faster,and it can also improve the static and transient stability of the power system effectively and improve control precision.
Terminal piecewise sliding mode;particle swarm optimization;excitation control;single machine infinite system
TM571
A
1003-3076(2014)06-0018-05
2013-06-08
张 虹(1973-),女,吉林籍,副教授,博士,研究方向为电力系统稳定与控制;于 雷(1988-),男,吉林籍,硕士研究生,研究方向为电力系统非线性控制。
