终端协同过程的中心节点自举算法研究

张志飞 凌志浩，2 高 冲

(华东理工大学化工过程先进控制与优化技术教育部重点实验室1，上海 200237;华东理工大学自动化系2，上海 200237)

0 引言

近年来，随着 WiFi Direct的兴起，其软接入点(access point，AP)功能为终端协同网络提供了参考的模型。研究协同交互过程的中心节点自举对组建WiFi的软AP协同网络具有重要意义。

作为终端协同的重要前提，服务及邻居发现指的是对周边服务及设备进行搜索和发现。Ad-hoc网络下的服务发现协议得到了广泛的研究，例如基于应用层的 PDP［1］、GSD［2］、SSD［3］和基于网络层的 DSDP［4］、AODV-SD［5］、M-ZRP［6］等;邻居发现的研究包括同步发现［7］和异步发现［8］的研究。本文考虑异步情况，异步情况更加贴近于实际的应用。近年来，基于约束图的多Agent一致性协调算法已经得到了控制领域的深入研究［9－10］。但是基于多Agent的终端协同及分布式IT系统依然少见。本文将借助多Agent一致性算法研究带通信约束的中心节点自举过程。

1 问题及描述

终端协同指通过终端之间的相互合作，为用户提供更加优良的服务体验，其过程包括服务及设备发现、互通及互操作等。为了更有效地进行组织和交互，无中心的分布式终端需要通过自举形成软AP，提供协同网络管理、服务及设备发现功能。软AP可以将分布式终端互发现转变为单向发现，其他终端只需要搜索该中心节点，即可找到协同网络中的所有节点，并能通过中心节点自动获取IP地址，申请加入该协同网络。因此，中心节点自举过程实现了从分布式Ad-hoc网络到具有软AP的层次网络的转变。

中心节点自举过程指对等网络中的各终端通过交互，在各自终端设备上执行中心节点自举算法，最终选举产生唯一的终端作为中心节点。

在自举过程中，面临着以下两个主要的问题:①各终端的时钟不一定严格同步，如何设计中心自举算法，以避免时钟异步对自举过程造成的影响;②在一定范围内不一定能够完全发现其他所有节点，如何在具有通信约束的网络中设计中心节点自举算法，以保证最终选举结果的一致性。

1.1 异步自举过程建模

异步自举过程指在初始时刻不同的情况下，通过自举产生唯一中心节点的过程。为了实现异步自举过程的描述，定义了以下变量:Tb为信号帧的时长，M为信道的个数。假设在信号帧之间存在Tb时长的空闲时间，那么完成一个帧信号的全部时长为2Tb。接收端工作于某一信道时，发送端可能工作于任何可能的信道，而只有在与接收端相同的信道上发送的信号才能被接收。如果发送端有M个信道，则需要长度为2TbM的发送时间。考虑到时钟的非同步性，需要增加2Tb的余量，所以发送端需要保证在2Tb(M+1)时长内在可用信道上连续发送信号帧。接收端为了确保与发送端可用信道有交集，需要在M个信道上进行轮询，这就使得发送端必须维持2Tb(M+1)M时长才能保证被接收端搜索到，T1=2Tb(M+1)M被称为搜索时长。

搜索时长示意图如图1所示。

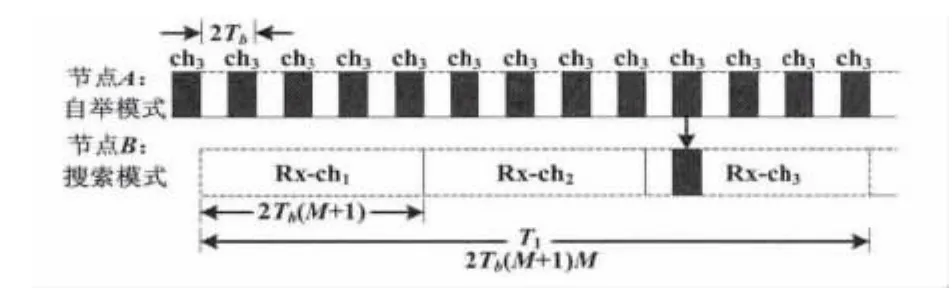
图1 搜索时长示意图Fig.1 Diagram of searching duration

为了更好地进行描述，可根据图1定义两种工作模式:搜索模式(scanning mode，SM)和自举模式(contending mode，CM)，并实现两者之间的切换。

①在搜索模式中，接收来自其他节点自举的信号。如果接收到来自其他节点的自举消息，则不再进行自举;如果执行T1时长后没有收到自举消息，则将自己推荐为中心节点，进入自举模式。

②在自举模式中，从某一信道连续发出自举消息，供其他节点搜索，执行的时长为xT1。其中，x为与参数有关的变量，体现终端之间的异构性。以剩余的能量为例，如果剩余能量越高，则x越大，相应的自举时间越长，也就越有可能成为中心节点。为了保证终端之间的异构性，也可选择ID号作为参数，因为ID号具有唯一性，ID号越大，能够获得的自举机会越多。

异步自举过程需要实现的目标是在节点时钟不同步的情况下，通过搜索模式和自举模式之间的切换，自举产生唯一的中心节点。

1.2 通信约束建模

通信约束表现为终端之间的直接互通所受到的限制，可以利用图论对其进行建模。以G=(V，E)表示网络拓扑，其中V={1，2，…，n}为节点集合，E⊆V×V为边的集合。节点的邻域为Ni={vj∈V(i，j)∈E}。节点只能向邻域内的节点进行信息的交互，而并不能与全网内的所有节点都进行信息交互。由于在同一条边上的两个节点既是CM中自举消息的发送端，也是SM 中自举消息的接收端，所以边(i，j)、(j，i)∈E，(i，j)=(j，i)的图为无向图。

1.3 一致性算法

图G=(V，E)中的一致性是通过局部的通信达成的。一致性达成指渐进收敛于一维空间的某一点x=αI，即 x1=x2= … =xn= α，其中 I=(1，…，1)T，α∈R为群组决策的结果。令A=［aij］为G的邻接矩阵，如果(i，j)∈E，则 aij=1;否则，aij=0。对于无向图，aij=aji。邻域 Ni={j∈V|(i，j)∈E}可以表示为 Ni={j∈V|aij≠0}，所有的边组成的集合可以定义为E={(i，j)∈V×V|aij≠0}。对于离散模型，分布式一致性算法可以描述为:

如果初始时刻各节点的状态为x(0)=(x1，…，xn)T，则各节点最终都收敛于空间中的某一点:

定义拉式矩阵L=D－A，其中D=diag(d1，…，dn)为 G 的度矩阵。D 中对角元素为 di=∑j≠iaij，其他非对角元素为0，则可以将式(1)改写为:

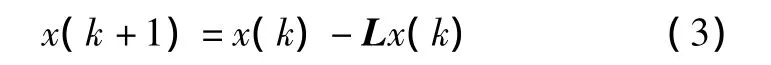
在最终达成一致时，由于x=αI，而LI=0，所以:

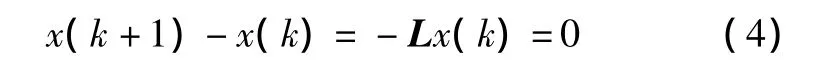
2 自举算法理论证明

2.1 异步自举算法

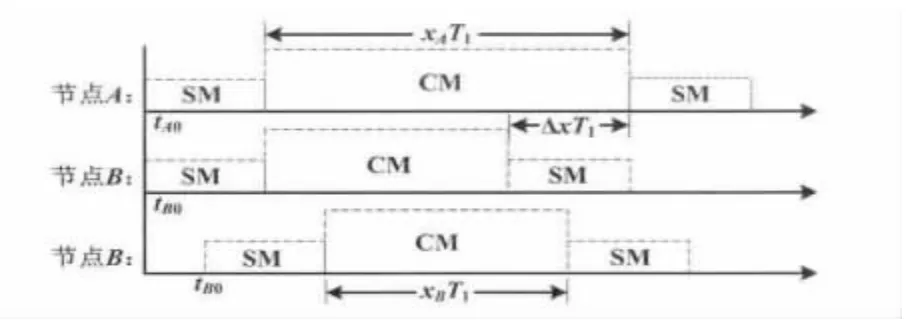
图2 双节点异步自举过程Fig.2 Asynchronous bootstrap between two nodes

定理1 两个节点利用如图2所示的异步自举过程，能够产生而且只能产生唯一的中心节点。

证明 由于A和B的地位对等，不失一般性，假设tA0=0，tB0≥0。当 ΔxT1＞0 时，如果 0≤tB0＜ T1，由于节点B的自举区间全部处于节点A的自举区间，节点A处于自举模式而节点B处于搜索模式的时长为T1。在获知节点A自举后，节点B将不再自举，从而使节点A成为中心节点。如果T1≤tB0，则节点B从tB0开始的搜索区间即可搜索到节点A发出的自举消息，并不再自举，从而A成为中心节点。当ΔxT1＜0即ΔxT1≤－T1时，如果0≤tB0＜T1，且 T1≤t≤T1+tB0内节点 B 能够搜索到节点A的自举消息，则A成为中心节点。如果节点A在自举失败后，则能够有大于T1长度的区间搜索来自节点B的自举消息，从而将节点B选举为中心节点。如果T1≤tB0，则节点B从初始时刻起就有等于T1长度的区间搜索来自节点A的自举消息，从而将节点A选举为中心节点。由于获得了搜索到自举节点的信号后节点就不进行自举，这样就保证了最终自举成功的中心节点的唯一性，证明完毕。

推论1 当 ΔxT1≤ －T1且 tB0≥T1时，xT1较小的节点才被选为中心节点。

证明 根据上述分析可知，其他情况下，xT1较大的节点均可能被自举为中心节点。

这也就说明，xT1较大的节点开始自举的时刻晚于xT1较小的节点，且初始时刻的差值大于T1时，xT1较小的节点才可通过优先自举的方法使得自己必然自举成功，成为中心节点。

2.2 通信约束一致性自举算法

在带有通信约束的情况下，不能像完全图那样通过一次信息交互就能获得所有节点的状态，需要通过与邻域内节点多次交互才能达成一致的自举结果。在每一次邻域内的交互过程中，与完全图中的自举算法一样，将自身状态值替换为邻域内的最大值。如果自身状态值本身就是最大值，则继续在该邻居内自举为中心节点。利用一致性算法描述自举过程为:

为了获得一致性自举算法的收敛的性质，需要定义道路和连通图。

定义从vi到vj的一条道路为:

如果对于任意的 vi，vj∈V，都存在 W(vi，vj)，则称该图为连通图。在连通图中，定义实现两点之间最短道路的跳数d(i，j)=m为两点之间最短路径(或距离)。连通图中最长距离定义为连通图的半径r=max{d(i，j)}。

连通图具有以下一致性收敛判断法则。

定理2 当且仅当无向图为连通图时，利用式(5)和式(6)所描述的一致性算法最终才能实现一致性收敛。

证明 首先证明充分性。由于通信图为连通图，不失一般性，假设vi，vj∈V，其中 vi为状态最大的节点，即 xi=max(x1，x2，…，xn)，则对于任意的其它节点vj∈V，根据连通图的定义可以找到该节点与vi之间的道路(7)。由于xi为最大值，通过一次迭代，便能影响其邻域内的所有节点状态，使其状态值变为xi。因此，节点 vi的状态可沿着道路 W(vi，vj)影响节点 v1，v2，…，vm－1，vm，vj的状态，最终实现道路上所有节点获得一致的状态xi=x1=…=xm=xj。由于vi为图中的任意节点，所以可推断最终能够使得图中所有的节点获得一致的状态x1=x2=…=xn，即通过实现一致性自举算法，可获得收敛的自举结果。再证明必要性。假设可一致性收敛，但不是连通图，则存在vi，vj∈V，不能找到这两节点之间的道路(7)。在此情形下，状态值最大的节点vi的状态就不能有效到达节点vj，最终vj的状态xj将小于xi，这与一致性收敛的假设相矛盾，所以该图必为连通图，证明完毕。

推论2 假设在某连通图半径为r，节点个数为n，实现一致性自举的最大迭代次数为k，则三者满足关系 k≤r≤n。

证明 由于r为图的半径，如果令任意两点间距离为d(i，j)=m，则由图的半径的定义可知，m≤r。最大迭代次数为从状态值最大的节点到距离其最远节点的跳数，即道路长为 k，k∈{m=d(i，j)}，所以 k≤r。同时，由于图的半径不大于节点数，即r≤n，得到k≤r≤n，得证。

3 算法仿真及结果分析

3.1 异步自举仿真

假设M=3，则完成一次搜索需要的时长2Tb(M+1)M=2Tb×12，因此可用12个离散的序列来模拟一次搜索中的发送和接收过程。对2.1节给出的异步自举算法进行数值模拟，验证算法的有效性。当0＜tBO＜ T1、ΔxT1＞0，0 ＜ tBO＜ T1、ΔxT1＞0，tB0≥T1、ΔxT1＜0，tB0≥T1、ΔxT1＜0 时，对应的仿真结果分别如图3～图6所示。

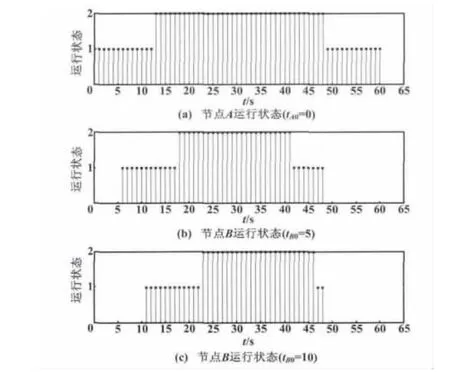
图3 自举仿真结果(1)Fig.3 Simulation results(1)

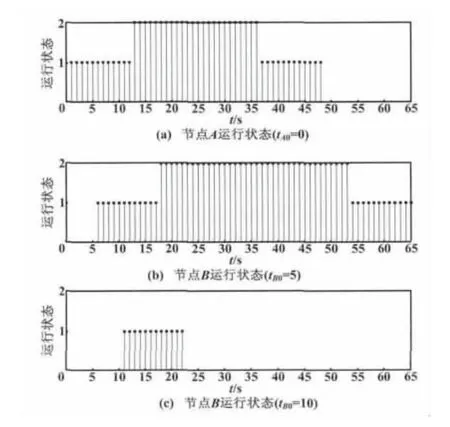
图4 自举仿真结果(2)Fig.4 Simulation results(2)

图5 自举仿真结果(3)Fig.5 Simulation results(3)

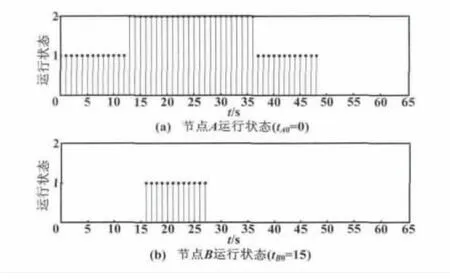
图6 自举仿真结果(4)Fig.6 Simulation results(4)

从仿真结果可以看出，对应于定理1中所述的各种异步情况，都能选出唯一的中心节点。从图5和图6可以看出，当tB0≥T1时，必然可以将节点B自举为中心节点，而与ΔxT1无关。因此即便是自举愿望不那么强烈，即x较小的节点也通过这种方式成功自举为中心节点，这也就验证了推论1。另外，值得注意的是，推论1为充分条件，并非必要条件。因为从图4可以看出，当0＜tB0＜T1时，x较小的节点也有机会成为中心节点，这取决于图1中所示的信道情况及tB0。如果在一次搜索中的第9个帧可以发现自举节点，那么当tB0＞9时，也可以实现节点A自举为中心节点。

3.2 通信约束条件下一致性自举仿真

假设n=10，带约束的通信图如图7所示。从图7可以看出，图的半径为 r=max{d(i，j)，i，j=1，2，…，10}=d(1，10)=6。

图7 带约束的通信图Fig.7 Communication with constraints

为了验证定理2及推论2，通过设置图7中各节点的初始状态值，并运行式(5)和式(6)所描述的一致性算法，通过多次迭代，实现全局收敛。仿真结果如图8所示。从图8(a)可以看出，当初始时刻节点6具有最大值时，通过3步即可实现全局收敛，这是因为从节点6到距离其最远的节点1和节点10的跳数为3。从图8(b)可以看出，当初始时刻节点1具有最大值时，由于到距离其最远的节点10的跳数为6，所以需要通过6步迭代才能实现最终收敛。从仿真结果可以看出，收敛时间取决于状态值最大的节点在图中位置的分布，并且收敛上界满足k≤r≤n。

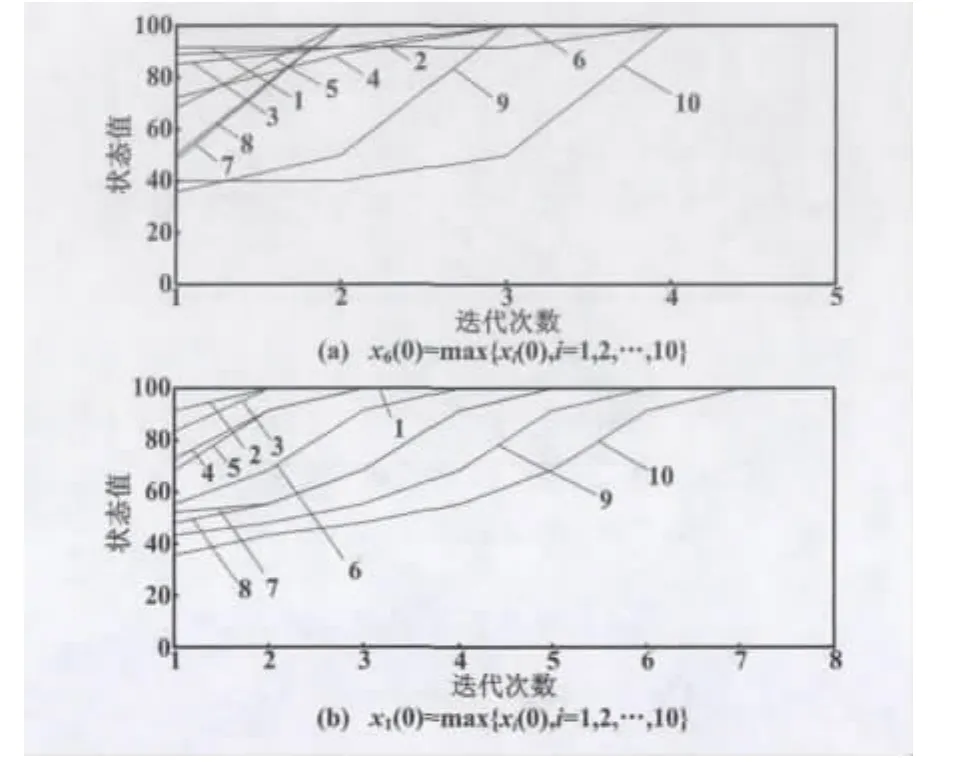
图8 带通信约束的一致性自举算法仿真结果Fig.8 Simulation results of consistency bootstrap algorithm with communication constraints

4 结束语

本文对泛在网络协同过程的中心节点自举算法进行了研究。针对无中心网络自举产生中心节点过程中所面临的时钟不同步和通信约束问题，提出了异步自举算法和带通信约束的一致性自举算法，并证明了算法的有效性和收敛性。在异步自举算法中，自举愿望较小的节点通过较早的自举成为中心节点，保证了各节点都具有成为中心节点的可能性。本文还给出了一致性自举算法中收敛时间的上界，不仅与网络规模有关，还与潜在中心节点在网络中所处的位置有关。不同的位置决定其到达距离最远的点的距离不同，收敛所需时间也不同。下一步工作将以本文研究结果为基础，对结合通信约束的异步自举算法进行深入研究。

［1］Song W C，Rehman S U，Lee K J，et al.Active PDP discovery for the policy based MANET management［J］.IEICE Transactions on Communication，2009，E92B(3):1027 －1030.

［2］Gao Z，Wang L，Yang M，et al.FNMGSDP:an optimized groupbased service discovery protocol for MANETs［J］.Wireless Personal Communications，2011，57(2):137 －162.

［3］Skjegstad M，Johnsen F T，Nordmoen J.An emulated test framework for service discovery and MANET research based on ns-3［C］//New Technologies，Mobility and Security(NTMS)，the 5thInternational Conference，2012:1 －5.

［4］Hwang C，Talipov E，Cha H.Distributed geographic service discovery for mobile sensor networks［J］.Computer Networks，2011，55(5):1069 －1082.

［5］Zhou X，Ge Y，Chen X，et al.SMF:A novel lightweight reliable service discovery approach in MANET［C］//Wireless Communications，Networking and Mobile Computing(WiCOM)，the 7thInternational Conference，2011:1 －5.

［6］Christopher N V，George C P.A routing layer based approach for energy efficient service discovery in mobile ad hoc networks［J］.Wireless Communications and Mobile Computing，2009，9(5):655 －672.

［7］Vasudevan S，Towsley D F，Goeckel D.Neighbor discovery in wireless networks and thecoupon collector’sproblem［C］//Mobile Computing and Networking(MOBICOM)，the 15thACM International Conference，2009:181 －192.

［8］Arachchige C J L，Venkatesan S，Mittal N.An asynchronous neighbor discovery algorithm for cognitive radio networks［C］//New Frontiers in Dynamic Spectrum Access Networks(DySPAN)，the 3rdIEEE Symposium，2008:704 －708.

［9］Martinez S，Cortes J，Bullo F.Motion coordination with distribution information［J］.IEEE Control Systems Magazine，2007，27(4):75 －88.

［10］Olfati-saber R，Fax J A，Murray R M.Consensus and cooperation in networked multi-agent systems［C］//Proceedings of the IEEE，2007，95(1):215－233.