一种基于阵列接收信号重排的单快拍DOA估计方法

2014-05-31蒋柏峰吕晓德向茂生

电子与信息学报 2014年6期

蒋柏峰吕晓德向茂生

蒋柏峰*①②吕晓德①向茂生①

①(中国科学院电子学研究所微波成像技术国家级重点实验室北京 100190)②(中国科学院大学北京 100049)

针对单快拍情况下大多数空间谱估计方法失效的问题，该文提出一种直接利用阵列接收信号重排构造伪协方差矩阵的模型。理论分析表明，该模型更加灵活且更具一般性，已有的伪协方差矩阵构造方法可以统一在该模型下。在此基础上结合波束形成的思想，进一步提出一种基于阵列接收信号加权求和的伪协方差矩阵构造方法，该方法综合考虑了信噪比及阵列自由度两方面因素的影响，可在一定程度上提升估计性能。理论分析和仿真验证说明了该方法及模型的正确性和有效性。

阵列信号处理；DOA估计；单快拍；伪协方差矩阵

1 引言

文献[9-14]直接给出了伪协方差矩阵的构造方式，并没有分析构造方法的来源；该构造方法要求可利用的单快拍数据个数为奇数，当数据个数为偶数时，将不可避免地浪费数据。本文从阵列接收信号模型入手，充分利用单快拍阵列接收信号的可用信息，推导出基于阵列接收信号重排方法的一般模型，理论推导证明，文献[9-14]中使用的构造方法可以统一在该模型下。在此基础上，结合数字波束形成思想，本文提出了一种基于加权求和的构造方法。该方法可充分利用单快拍数据，更具一般性，并且可在一定程度上提高信噪比，减小噪声带来的影响。仿真试验验证了构造方法的正确性和有效性。

2 伪协方差矩阵构造模型

远场窄带信号假设下的均匀线阵接收信号模型可表示为[16]

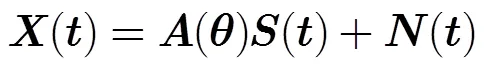
理想情况下，信号之间是不相关的，信号与噪声之间、各通道噪声之间是相互独立的，此时阵列接收信号的协方差矩阵可表示为

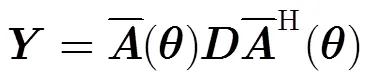
忽略噪声项的影响，可利用的信息可表示为

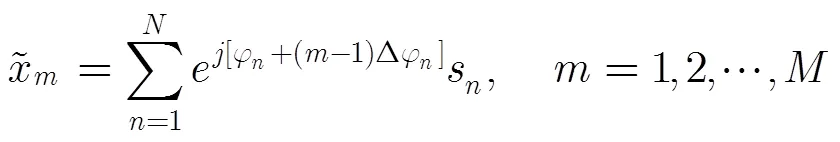
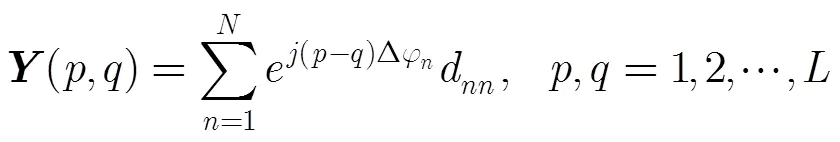
3 伪协方差矩阵构造方法

3.1 直接数据域方法

3.2 加权求和方法

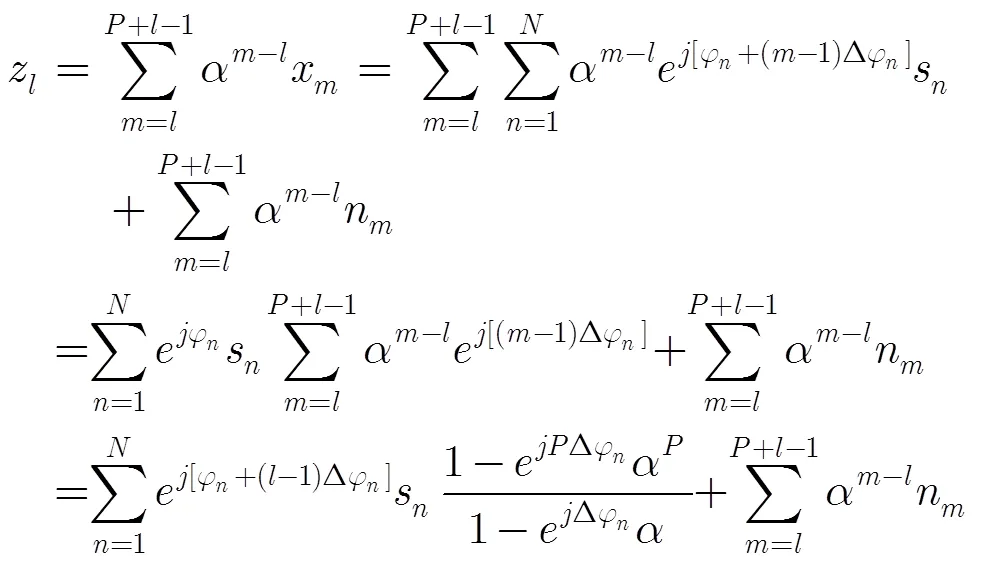
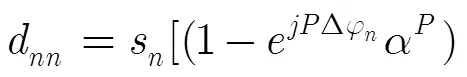
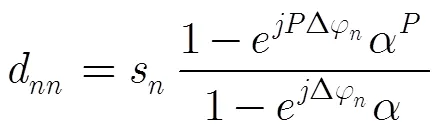
4 仿真试验及分析

本文提出的模型及构造方法可以认为是单快拍情况下的一类预处理方法，可与多种空间谱估计方法结合。为方便比对，仿真时均结合使用MUSIC算法。

从图1(a)可以看出，随着信噪比的增加，3种方法的估计成功概率都增加，当信噪比增加到10 dB时，3种方法的成功概率都为1。在信噪比较低时，本文方法的成功概率是3种方法中最高的，这在一定程度上体现了加权求和带来的信噪比提升。从图1(b)可以看出，随着信噪比的增加，3种方法的估计均方根误差逐渐减小并趋于0。相比基于多快拍的MUSIC算法，本文方法及文献[9-14]方法的性能有所下降，尤其是在低信噪比情况下，性能恶化更为严重。这主要是因为与常规多快拍方法相比，单快拍方法利用的信息量更少，缺少多快拍带来的信号积累和对噪声的抑制。在信噪比较低时，本文方法的估计均方根误差小于文献[9-14]的方法，这主要是因为低信噪比时，噪声对估计性能的影响占主要地位，本文的加权求和方法使得信号比有所提升，因此性能较好；而在高信噪比时，本文方法的估计均方根误差比文献[9-14]方法略差，此时影响估计性能的主要因素是阵列自由度，不再是噪声。

4.2 阵列自由度与加权求和的折中

由前文介绍可知，加权求和方法可在一定程度上提升信噪比，参与求和的项越多，提升效果越明显，但是求和后构造的伪协方差矩阵自由度越小。因此，存在一个求和项数量与阵列自由度的折中。下面通过仿真说明这个问题。

4.3 不同波束指向时的估计性能

5 结束语

针对单快拍情况下大多数空间谱估计方法失效的问题，本文以均匀线阵下的远场窄带信号接收模型为基础，提出了基于阵列接收信号重排的伪协方差矩阵构造模型。该模型完善了基于接收信号重排的单快拍DOA估计方法体系，理论分析和推导证明了文献[9-14]使用的方法可以统一在该模型下。在此基础上，结合数字波束形成的思想，本文提出了一种基于阵列接收信号加权求和的伪协方差矩阵构造方法，该方法更具一般性。通过对单快拍数据的加权求和，该方法可一定程度上提升信噪比，改善估计性能。本文提出的伪协方差矩阵构造模型，针对的是基于特征分解的空间谱估计方法，当使用奇异值分解时，伪协方差矩阵的结构将更加灵活，这种情况下的伪协方差矩阵构造模型将是下一步的工作重点。

图1 3种方法估计性能对比

图2 不同阵列规模时估计性能对比

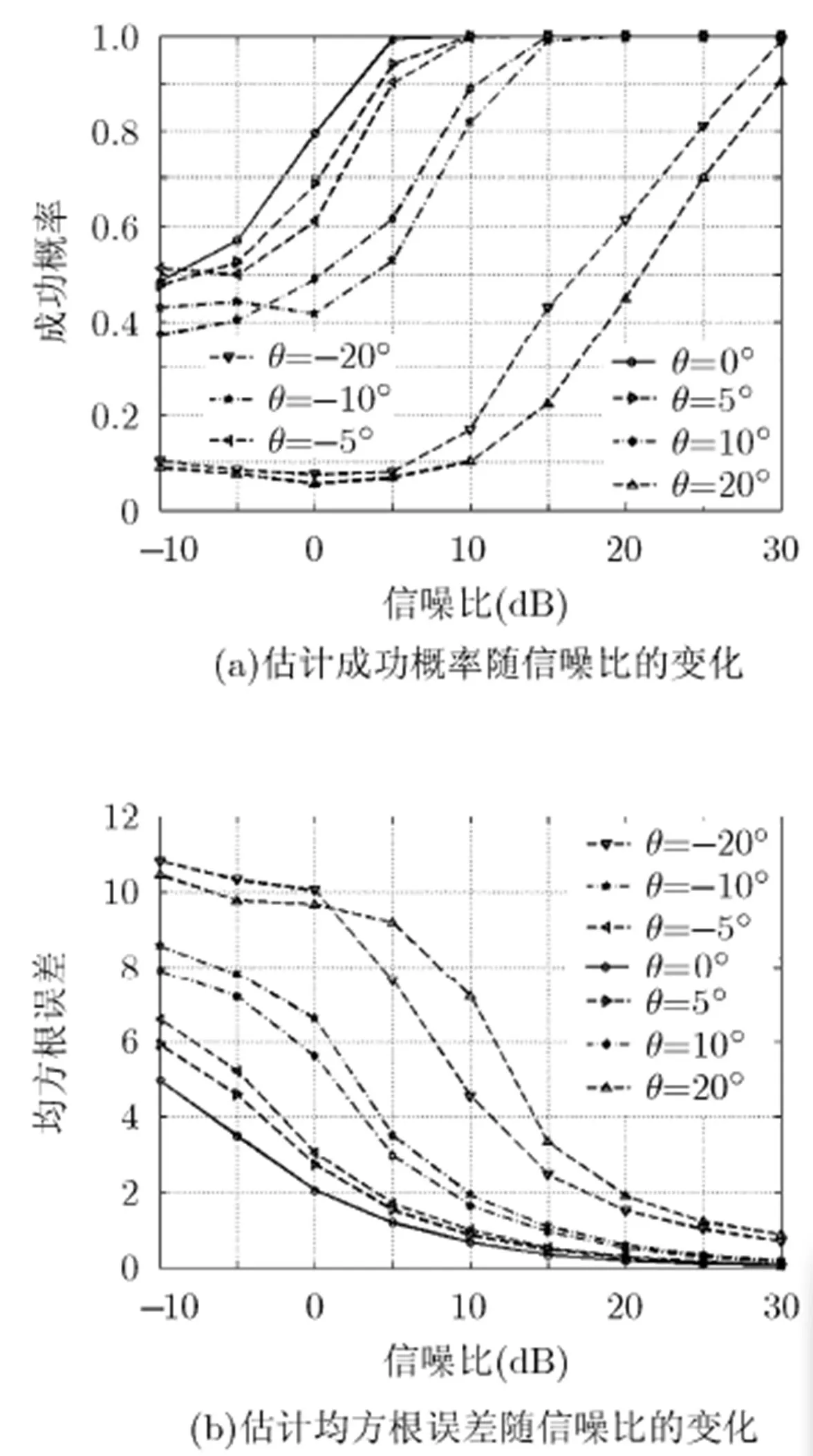
图3 不同波束指向时的估计性能对比

[1] Schmidt R O. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280.

[2] Roy R and Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]., 1989, 37(7): 984-995.

[3] Alcala B E and Recio F R. Performance analysis of metaheuristic approaches for single-snapshot DOA estimation[J]., 2013, 12(1): 166-169.

[4] Errasti-Alcala B and Fernandez-Recio R. On the use of particle swarm optimization for single snapshot DOA and frequency estimation[C]. Proceedings of 2013 6th European Conference on Antennas and Propagation, Prague, 2012: 3635-3639.

[5] Zaman F, Khan J A, Khan Z U,An application of hybrid computing to estimate jointly the amplitude and direction of arrival with single snapshot[C]. Proceedings of 2013 10th International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, 2013: 364-368.

[6] Sheikh Y A, Zaman F, Qureshi I M,. Amplitude and direction of arrival estimation using differential evolution[C]. International Conference on Emerging Technologies, Islamabad, 2012: 1-4.

[7] Ren Q S and Willis A J. Extending MUSIC to single snapshot and on line direction finding applications[C]. IEE Radar’97, Edinburgh, UK, 1997: 783-797.

[8] Kim J T and Han D S. Fast DOA estimation algorithm using pseudo covariance matrix[C]. IEEE Vehicular Technology Conference. Orlando Florida, 2003: 519-523.

[9] Mort N P and Nizar T. Propagator method triangular factorization for source bearing estimation of coherent sources[C]. IEEE Military Communications Conference, Orlando, Florida, 2007: 29-31.

[10] 万群, 彭应宁, 杨万麟. 单次快摄的局部散射源中心波达方向估计方法[J]. 电子学报, 2003, 31(6): 809-811.

Wan Qun, Peng Ying-ning, and Yang Wan-lin. Nominal direction of arrival estimation for locally scattered source using single snapshot data[J]., 2003, 31(6): 809-811.

[11] 王凌, 李国林, 隋鉴, 等. 单次快拍波达方向矩阵法[J]. 系统工程与电子技术, 2012, 34(7): 1323-1328.

Wang Ling, Li Guo-lin, Sui Jian,Single snapshot DOA matrix method[J]., 2012, 34(7): 1323-1328.

[12] 王凌, 李国林, 谢鑫. 互耦效应下应用单快拍数据实现相干信源完全解相干和解耦合[J]. 电子与信息学报, 2012, 34(10): 2532-2536.

Wang Ling, Li Guo-lin, and Xie Xin. Decorrelation an decoupling of coherent signals in the presence of mutual coupling using signal snapshot[J].&, 2012, 34(10): 2532-2536.

[13] 王凌, 李国林, 孟晶, 等. 用一次快拍数据实现二维完全解相干和解互耦[J]. 系统工程与电子技术, 2012, 34(11): 2208-2213.

Wang Ling, Li Guo-lin, Meng Jing,. Two-dimensional decorrelation and decoupling using single snapshot[J]., 2012, 34(11): 2208-2213.

[14] 马永阳, 李春晓, 杨杰. 一种基于单快拍的DOA估计算法[J]. 杭州电子科技大学学报, 2012, 32(5): 45-48.

Ma Yong-yang, Li Chun-xiao, and Yang Jie. DOA estimation based on single snapshot[J]., 2012, 32(5): 45-48.

[15] 谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA估计[J]. 电子与信息学报, 2010, 32(3): 604-608.

Xie Xin, Li Guo-lin, and Liu Hua-wen. DOA estimation of coherent signals using one snapshots[J].&, 2010, 32(3): 604-608.

[16] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004: 19-30.

WangYong-liang, Chen Hui, Peng Ying-ning,.. Spatial Spectrum Estimation Theory andAlgorithms[M]. Beijing: Tsinghua University Press, 2004: 19-30.

蒋柏峰：男，1987年生，博士生，研究领域为阵列信号处理、无源雷达信号处理.

吕晓德：男，1969年生，研究员，研究方向为基于阵列技术的新体制雷达系统及其应用.

向茂生：男，1964年生，研究员，主要研究方向为雷达信号处理、干涉合成孔径雷达技术.

Single Snapshot DOA Estimation Method Based on Rearrangement of Array Receiving Signal

Jiang Bai-feng①②Lü Xiao-de①Xiang Mao-sheng①

①(,,,100190,)②(,100049,)

Most of spatial spectrum estimation methods fail when there is only one valid snapshot. To deal with this issue, a pseudo covariance matrix construction model utilizing array receiving signal is proposed. Theoretical analysis shows that the presented model, which consists in the existing methods, is more flexible and general. Combining with beam forming idea, a method based on weighted summarizing is proposed, which considers both the affections of signal-to-noise ratio and array freedom. Estimation performance can be enhanced in some degree. Theoretical analysis and simulation results verify the correctness and effectiveness of the proposed method and model.

Array signal processing; DOA estimation; Single snapshot; Pseudo covariance matrix

TN911.7

1009-5896(2014)06-1334-06

10.3724/SP.J.1146.2013.01242

蒋柏峰 jbf_gucas@163.com

2013-08-19收到，2013-11-01改回