基于三角函数拟合的RCS序列进动周期估计

张仕元



基于三角函数拟合的RCS序列进动周期估计

张仕元*

(南京电子技术研究所 南京 210039)

利用雷达反射截面(RCS)序列估计进动周期为弹道目标特征提取和识别的重要途径。弹道目标在进动时，回波RCS序列为非平稳的周期序列，常规Fourier变换方法和周期间相关类方法需要较长观测时间和较高数据率才能有效地估计RCS的周期，这对于有限的雷达资源来说是不可接受的。该文提出一种新的估计弹道目标RCS序列周期的方法，该方法先利用特定频率附近的三角函数来拟合RCS序列，再求得使拟合误差最小的频率，即为RCS序列的进动频率。相比于常规方法，该文方法具有所需资源少，估计精度高的特点。RCS计算数据的仿真结果证明了该文方法的有效性。

弹道导弹目标；雷达反射截面序列；进动周期；三角函数拟合

1 引言

2 锥体目标RCS的周期特性

2.1 锥体目标进动姿态角变化

弹头与母舱分离过程中，弹头会受到冲击力矩的作用，力矩消失后弹头在自旋的同时极轴在平衡位置作圆锥运动，称为进动。进动弹头目标在中段飞行过程中的一个主要特征，可用进动角和进动频率来描述。

图1 锥体进动示意图

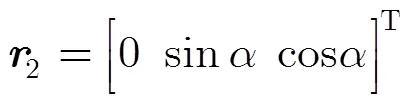
雷达视线与目标轴线夹角(即姿态角)的方向余弦为

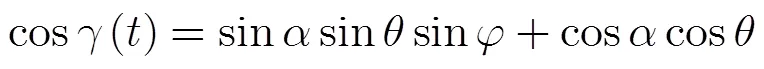
故姿态角随时间变化公式为

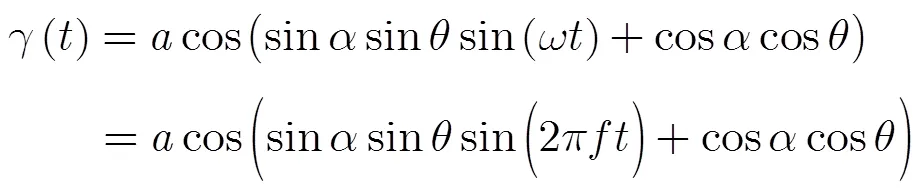
2.2 锥体目标RCS的周期性

由式(4)可知，姿态角的周期与弹头的进动周期一致。当雷达位置固定时，中段自旋稳定目标姿态角的变化主要由3部分引起，即自旋、进动和平动。对于锥体类完全体对称目标，雷达和目标相对姿态角主要由进动和平动引起。平动引起的姿态变化是一种慢变化，而进动引起的姿态变化是一种快变化，因此目标总的姿态变化可视为在慢变化上迭加上了快变化，其中快变化与进动具有一致的周期性。由目标的散射特性[15,16]可知，目标的雷达姿态角变化是引起RCS起伏的最主要原因，当姿态角呈现周期性时，相应的RCS也会呈现周期性变化。采用电磁计算软件对锥体目标进行电磁计算，得到具有进动特性目标的RCS曲线如图2所示，其中目标的进动周期设为1 Hz。

由图2可知，进动目标的RCS呈现明显的周期特性，同时受多种因素的影响，RCS曲线表现出非平稳性。在低信噪比条件下，RCS测量存在一定的误差，这些都使得RCS的周期估计变得十分困难。因此，寻找一种稳健的RCS周期估计方法变得十分重要。

3 基于三角函数拟合的RCS序列周期估计

现有提取RCS序列周期的方法有傅里叶变换法和自相关函数法、幅度差函数法、幅度差结合自相关函数法的周期相关类方法，以及循环周期相关类方法。傅里叶变换法是对信号的整体分析，要求信号是平稳的，且估计精度受限于信号时宽。周期相关法本质上是利用信号的周期间的相关性，故对观测时间要求较高，一般要有两倍进动周期以上的观测时间，且当实际进动周期较大时，周期相关类方法的尾样点值由于求和项的减少而使周期估计失效；而循环周期相关类方法虽然可以避免求和项减少而使周期估计失效，但对RCS采样序列的循环平稳性要求更高，这在实际上是不太可能的。故需要寻求RCS周期估计的新方法。

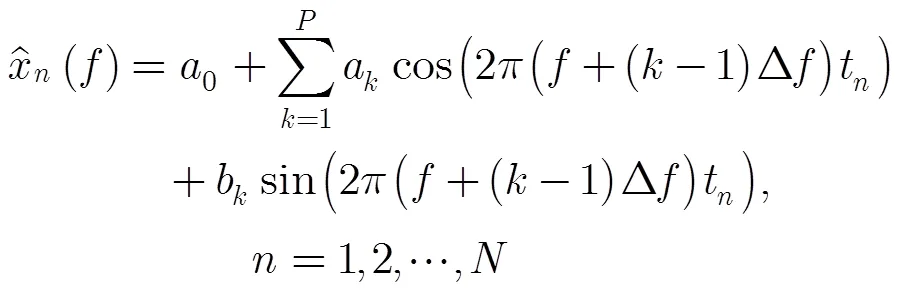
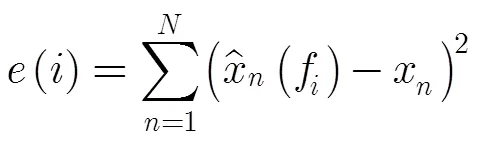
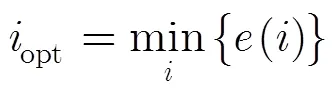
对应的频率为

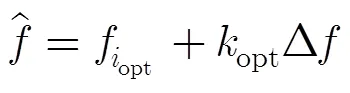
即为RCS序列的进动频率。式中

4 仿真实验

仿真实验以某外军导弹为仿真模型，模拟弹头在中段飞行过程中，雷达所观测到的RCS序列。雷达工作频段为X波段，位置布置在弹头落点附近。RCS数据为电磁计算软件，弹头为长度为1.875 m的均匀光滑轴对称平底锥体，模型尺寸如图3所示。

图4为观测时间为4 s，数据率为20 Hz，信噪比为20 dB时，实际进动频率为1.25 Hz 的去直流RCS序列(图中实线)，以及采用本文三角函数拟合法所得的拟合曲线(图中点划线)。由图4可知，RCS序列的周期性在噪声的影响下已不明显，非平稳性加强。图5所示为针对图4中的RCS序列，应用本文方法所得的拟合误差曲线，由图可知，拟合误差最小的频率点为1.22 Hz，即本文方法估计的RCS序列进动频率为1.22 Hz。由图4和图5可知，三角函数拟合法的分数频率分量的引入，在观测时间内可以适应这种不平稳性。图6和图7示出了在同样条件下，分别采用Fourier变换法和循环幅度差加权自相关函数法的幅度分布。由图6可知Fourier变换幅度分布的峰值点对应处的频率为5 Hz，即Fourier变换法不能适应RCS序列的不平稳性而使估计误差加大。图7中循环幅度差加权自相关函数的峰值出现在时延为1.6 s的位置，对应的频率为0.625 Hz，即循环幅度差加权自相关函数法估计的进动频率为0.625 Hz。由图7还可知，循环幅度差加权自相关函数法的分频和倍频现象比较明显。对比图5，图6和图7可知，本文方法的估计结果较准确。

图8示出了在观测时间为4 s，信噪比为20 dB，数据率为20 Hz时，针对不同进动频率的RCS序列，本文方法经过400次蒙特卡罗实验所得进动频率均方根误差。为了对比，也示出了Fourier变换和幅度差加权自相关函数的进动频率估计的均方根误差。由图可知，本文方法的估计误差最小，周期相关类方法只在部分频点与三角函数拟合法相当，大部分频点的估计误差为本文方法的2倍多，而Fourier变换法的估计误差最大。

图9所示为为观测时间为4 s，数据率为20 Hz时，不同信噪比时，3种方法针对不同进动频率的平均均方根误差曲线。由图可知，随着信噪比的提高，3种方法的平均均方根估计误差都降低，信噪比达30 dB以后，3种方法的平均均方根误差改善都不大。由图还可知，本文方法的平均均方根误差最小，在信噪比为25 dB时平均估计均方根误差小于0.13 Hz，可满足工程应用的需要。

图10所示为观测时间为4 s，信噪比为25 dB时，针对不同的数据率，3种方法的平均进动频率估计均方根误差。由图可知，随着数据率的提高，3种方法的估计精度都提高，数据率为30 Hz以后，估计精度改善已不明显。其中，本文方法的平均均方根误差最小，在数据率为20 Hz时，平均均方根误差为0.128 Hz，数据率为25 Hz时，平均估计均方根误差为0.086 Hz。

图2 锥体进动的RCS曲线

图3 某弹头模型结构示意图

图4 进动周期为1.25 Hz的RCS序列与三角函数拟合序列对比

图5 三角函数拟合法对进动频率为1.25 Hz的RCS序列不同频率点的拟合误差

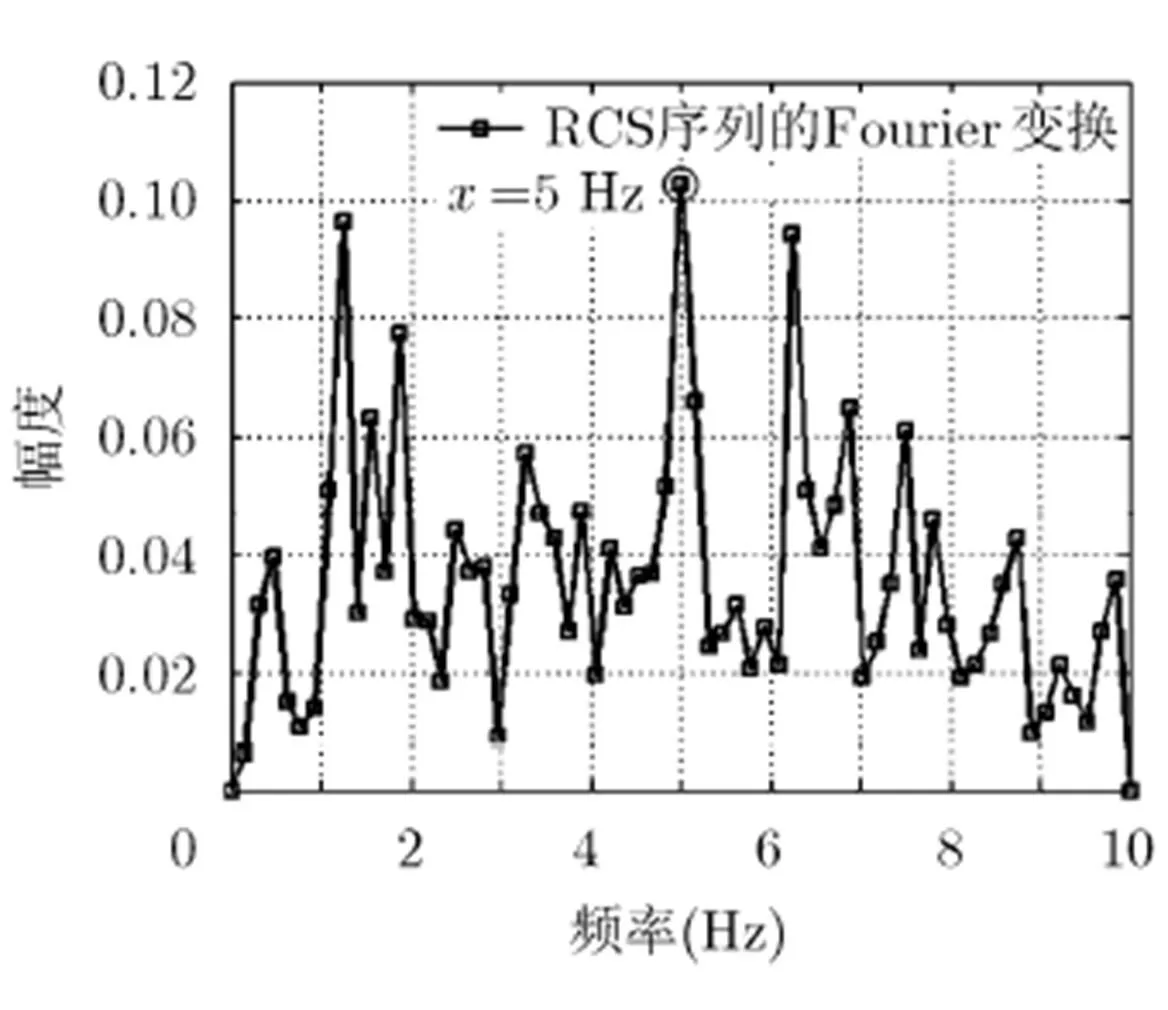
图6 进动频率为1.25 Hz的RCS序列去直流后的Fourier变换幅度

图7 进动频率为1.25 Hz的RCS序列的循环幅度差加权自相关函数

图8 不同进动频率时本文方法、Fourier变换法和滑窗相关类方法的估计均方根误差　　　　　　　　

图9 不同信噪比时本文方法、Fourier变换法和滑窗相关类方法的平均均方根误差

图10 不同数据率时本文方法、Fourier变换法和滑窗相关类方法的平均均方根误差

综合图9和图10可知，在相同的数据率或相同的信噪比条件下，本方方法的估计精度都高于Fourier变换方法和周期间相关类方法。在数据率为20 Hz，信噪比达25 dB以上时，平均估计误差低于0.13 Hz，能满足工程应用的需要。

5 结束语

本文提出了一种估计RCS序列周期的新方法。该方法用某个频率点附近的三角函数来拟合RCS序列，使得拟合误差最小的频率就是RCS序列的频率。仿真实验表明，本文方法在较短的观测时间(4 s)和较小的数据率(20 Hz左右)，信噪比达25 dB以上时，可获得较好的估计精度，从而为反导目标识别提供了一个有意义的思路。

[1] Chen V C, Li F Y, and Ho S S. Micro-doppler effect in radar-phenomenon, model and simulation study[J]., 2006, 42(1): 2-21.

[2] 郑建成, 王党卫, 马晓岩, 等. 基于自旋运动的高速弹头成像方法[J]. 雷达学报, 2013, 2(3): 300-308.

Zheng Jian-cheng, Wang Dang-wei, Ma Xiao-yan,.. Study on spin-based imaging of high-speed warhead[J]., 2013, 2(3): 300-308.

[3] Liu Yong-xiang, Li Xiang, Zhuang Zhao-wen,.. Estimation of micro-motion parameters based on micro- doppler[J]., 2010, 4(3): 213-217.

[4] Cai Cheng-jie, Liu Wei-xian, and Fu J S. Radar micro-doppler signature analysis with HHT[J]., 2010, 46(2): 930-938.

[5] 雷腾, 刘进忙, 李松, 等. 弹道目标进动周期特征提取新方法[J]. 计算机工程应用, 2013, 49(1): 265-270.

Lei Teng, Liu Jin-mang, Li Song,.. Novel micro-doppler signature extraction method of ballistic midcourse target[J]., 2013, 49(1): 265-270.

[6] He Si-san, Zhou Jian-xiong, Zhao Hong-zhou,.. Estimating the procession angle of ballistic targets in midcourse based on HRRP Sequence[C]. IEEE Radar Conference, Rome, Italy, 2008: 1-4.

[7] 毕莉, 赵锋, 高勋章, 等. 基于一维像序列的进动目标尺寸估计研究[J]. 电子与信息学报, 2010, 32(8): 1825-1830.

Bi Li, Zhao Feng, Gao Xun-zhang,.. Study on processional target’s dimension estimation based on HRRPs [J].&, 2010, 32(8): 1825-1830.

[8] 雷腾, 刘进忙, 余付平. 基于时间－距离像的弹道目标进动特征提取新方法[J]. 信号处理, 2012, 28(1): 73-79.

Lei Teng, Liu Jin-mang, and Yu Fu-ping. A new procession signature extraction method of ballistic target based on range-profile[J]., 2012, 28(1): 73-79.

[9] Liu Li-hua, Wang Zhuang, and Hu Wei-dong. Procession period extraction of ballistic missile based on radar measurement[C]. CIE International Conference on Radar, Shanghai, China, 2006: 1-4.

[10] 张渊, 张爱成. 利用FFT方法分析自旋目标RCS变化周期[J]. 飞行器测控学报, 2012, 31(1): 26-29.

Zhang Yuan and Zhang Ai-cheng. Analysis of the RCS variation cycle of spin-stabilized objects using FFT method [J].&, 2012, 31(1): 26-29.

[11] 陈翱. 基于RCS序列的弹道中段目标微动提取技术[J]. 现代雷达, 2012, 34(6): 78-81.

Chen Ao. A micromoton extraction technique for target in intermediate trajectory based on RCS sequence[J]., 2012, 34(6): 78-81.

[12] Ross M and Shafer H. Average magnitude difference function pitch extractor[J]., 1974, 22(5): 355-362.

[13] 冯德军, 丹梅, 马梁. 一种鲁棒的弹道目标RCS周期估计方法[J]. 航天电子对抗, 2008, 24(2): 5-8.

Feng De-jun, Dan Mei, and Ma Liang. A robust RCS periodicity estimation algorithm for ballistic target[J]., 2008, 24(2): 5-8.

[14] 康猛, 王春花, 郝明, 等. 弹道目标进动周期特征提取研究[J]. 现代雷达, 2010, 32(11): 29-32.

Kang Meng, Wang Chun-hua, Hao Ming,.. A study of procession-period extraction method of ballistic target[J]., 2010, 32(11): 29-32.

[15] 资文荗, 毕义明, 康璞. 弹道中段RCS控制研究[J]. 舰船电子工程, 2012, 32(7): 82-84.

Zi Wen-mao, Bi Yi-ming, and Kang Pu. Study of radar cross section control in ballistic missile midcourse[J]., 2012, 32(7): 82-84.

[16] 黄培康, 殷红成, 徐小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 86-92.

Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Characteristic[M]. Beijing: Publishing House of Electronics Industry, 2005: 86-92.

张仕元： 男，1975年生，博士，高级工程师，主要研究方向为雷达目标检测与识别.

Procession Period Estimation of RCS SequencesBased on Trigonometric Function Fitting

Zhang Shi-yuan

(,210039,)

Estimating procession period based on ballistic missile target’s Radar Cross Section (RCS) sequences is an important means of feature extraction and target identification. The RCS sequences of ballistic missile target are unstable random process when the target is in procession, and the conventional Fourier transform and correlation type method needs long observation time and high data rate to estimate the procession period, which are unacceptable to the limited radar resource. A novel method of estimating procession period based on RCS sequences is presented. The proposed method first fits the RCS sequences with trigonometric function of a certain frequency, then get a procession frequency that minimize the fitting errors of different frequencies’ trigonometric function. The proposed method estimate more accurately and needs fewer time resources than conventional ones, as is validated by the simulation results of RCS data.

Ballistic missile target; Radar Cross Section (RCS) sequences; Procession period; Trigonometric function fitting

TN953

A

1009-5896(2014)06-1389-05

10.3724/SP.J.1146.2013.01716

张仕元 zsyradar@163.com

2013-11-04收到，2014-03-27改回

中国电子科技集团公司创新基金(JJ11165)资助课题