基于空频相关性的大规模MIMO-OFDM信道压缩反馈算法

李晓辉 王维猛 黑永强



基于空频相关性的大规模MIMO-OFDM信道压缩反馈算法

李晓辉*王维猛 黑永强

(西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071)

大规模MIMO-OFDM系统中，信道常常存在较强的空间和频域相关性。针对多数信道压缩反馈算法仅考虑空间或频域相关性的问题，该文提出一种空频联合压缩反馈算法。首先，根据压缩感知理论进行了信道空频2维稀疏度分析；然后，推导了信道矩阵在空间和频域2维相关性下的联合稀疏基；最后，利用该联合稀疏基给出了空频联合压缩算法。仿真结果与分析表明，该算法在保证信道反馈精度的同时，可显著降低反馈量。

无线通信；MIMO-OFDM；压缩反馈；空频相关性

1 引言

大规模多输入多输出(Multiple Input Multiple Output, MIMO)系统在基站端使用数以百计的低功耗天线，通过波束赋形使得传输信号的能量更明确地指向期望方向，提升接收端的信噪比，提升系统吞吐量[1]。然而，为了通过使用大规模MIMO获得性能增益，基站需要获取信道状态信息(CSI)。信道状态信息的获取可通过信道互易性，也可通过反馈获得。但是，信道互易性并不适用于频分双工(Frequency Division Duplexing, FDD)系统。由于天线数过多，传统的信道信息反馈降低方法，如矢量量化方法和基于码本的方法等并不适用于大规模MIMO系统[2]。此外，未来移动通信系统中常常采用正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)和MIMO相结合的传输模式，不同子载波的信道反馈也会加剧反馈带来的开销。因此，需要设计有效的算法来降低大规模MIMO-OFDM系统的反馈开销。

近年来，压缩感知(Compressed Sensing, CS)理论被广泛应用于信号处理和通信领域，为研究信道的压缩反馈提供了新的思路。使用压缩感知降低MIMO-OFDM系统中反馈量的方法主要从空间和频域两个角度来考虑。由于大规模MIMO-OFDM系统的天线间距小，信道往往具有较强的空间相关性[1,2]。文献[1]利用了大规模MIMO的空间相关性，提出了信道模拟压缩反馈方法，以更小的功率和更短的时间获得了更好的反馈性能；文献[2]也使用压缩感知从空间角度来降低反馈开销，提出了根据信道状态变化自适应调整压缩比和将卡洛南-洛伊变换(Karhunen-Loeve Transform, KLT)，离散余弦变换(Discrete Cosine Transform, DCT)相结合的两种自适应压缩算法，进一步提升了反馈效率。在频域角度，文献[3]指出当信道多径数远远小于子载波数时，频域信道矩阵在快速傅里叶变换(Fast Fourier Transform, FFT)矩阵上是稀疏的，也就是使用FFT变换矩阵作为频域稀疏基可得到频域信道的最稀疏表示。文献[4-6]指出相邻子载波上的信噪比具有高度相关性，所有子载波上信噪比构成的信号是一种稀疏可压缩的信号，并提出在频域采用基于压缩感知理论的压缩反馈方法，在相同的反馈条件下获得更好的系统吞吐量性能。文献[7]在压缩反馈的基础上提出了基于特征值的反馈算法，进一步提高了压缩和反馈效率。

2 系统模型

其中表示用户在子载波上的波束成形矢量。经过信道传输后，第个用户在第( )根接收天线第个子载波上收到的信号可以表示为

3 基于空频相关性的信道压缩反馈

3.1 压缩感知简介

3.2 信道空频稀疏度分析

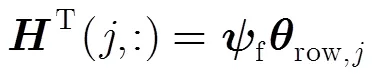
引理1 对于一个2维矩阵，如果矩阵的行与行之间是相关的，矩阵的列与列之间也是相关的，则该2维矩阵左乘一个正交矩阵，并不会改变矩阵行与行之间的相关性。同理，对此矩阵右乘一个正交矩阵，不会改变矩阵列与列之间的相关性。

证明 如果一个矩阵是正交矩阵，那么此矩阵是一个可逆矩阵，同时矩阵可逆等价于此矩阵可表示为若干个同阶初等矩阵的乘积，所以矩阵同一个正交矩阵相乘，相当于此矩阵和一系列初等矩阵的乘积相乘，根据矩阵初等变换的性质，并不会改变此矩阵另一维的特性。

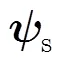
3.3 基于空频相关性的信道压缩反馈算法

本节分3部分来介绍所提的新算法：一是推导了空频联合稀疏基，二是给出了算法的具体实现过程，三是分析了算法的反馈量。

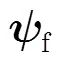
于是可以得到

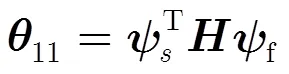
根据文献[9]中式(496)可得

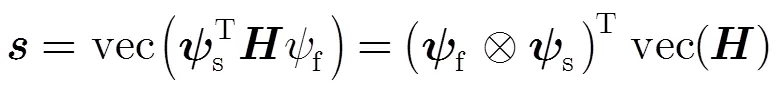
3.3.2算法具体实现 根据上面的分析和推理，本文给出使用基于空频相关性的信道联合压缩算法的具体流程图，如图2所示

根据图2所示，所提出的新的信道压缩反馈算法的具体步骤为：

图2 信道联合压缩反馈算法流程图

4 仿真与性能

4.1仿真与性能分析

对比信道稀疏表示前后的信道增益直方图，通过观察稀疏表示前后信道的特性变化来说明本文采用的稀疏表示方法的有效性。为使图形更清晰，我们仅画出其中64根天线64个子载波的情形，分别如图3(a)和图3(b)所示。

由图3 (a)和图3(b)可以看出，在对信道进行稀疏表示前，信道增益在不同的发射天线和不同的子载波上，其增益值均是非零的，而且也不符合指数衰减的规律，不过信道增益在发射天线之间，子载波之间存在着相关性；经过信道稀疏表示后，信道增益可用有限个非零值进行表示，说明本文提出的稀疏表示方法是有效的。对比可看出，本文提出的联合稀疏算法是有效的，可获得信道信息的最稀疏表示。

下面采用上文推导出的稀疏基来对信道矩阵进行压缩，然后再对信道矩阵进行恢复，并与原来的算法进行对比。对于空间的相关性，采用DCT稀疏基，对于频域的相关性，采用FFT变换稀疏基，对于联合利用空间相关性和频域间的相关性，采用所提算法推导出的稀疏基。仿真曲线如图4和图5所示。

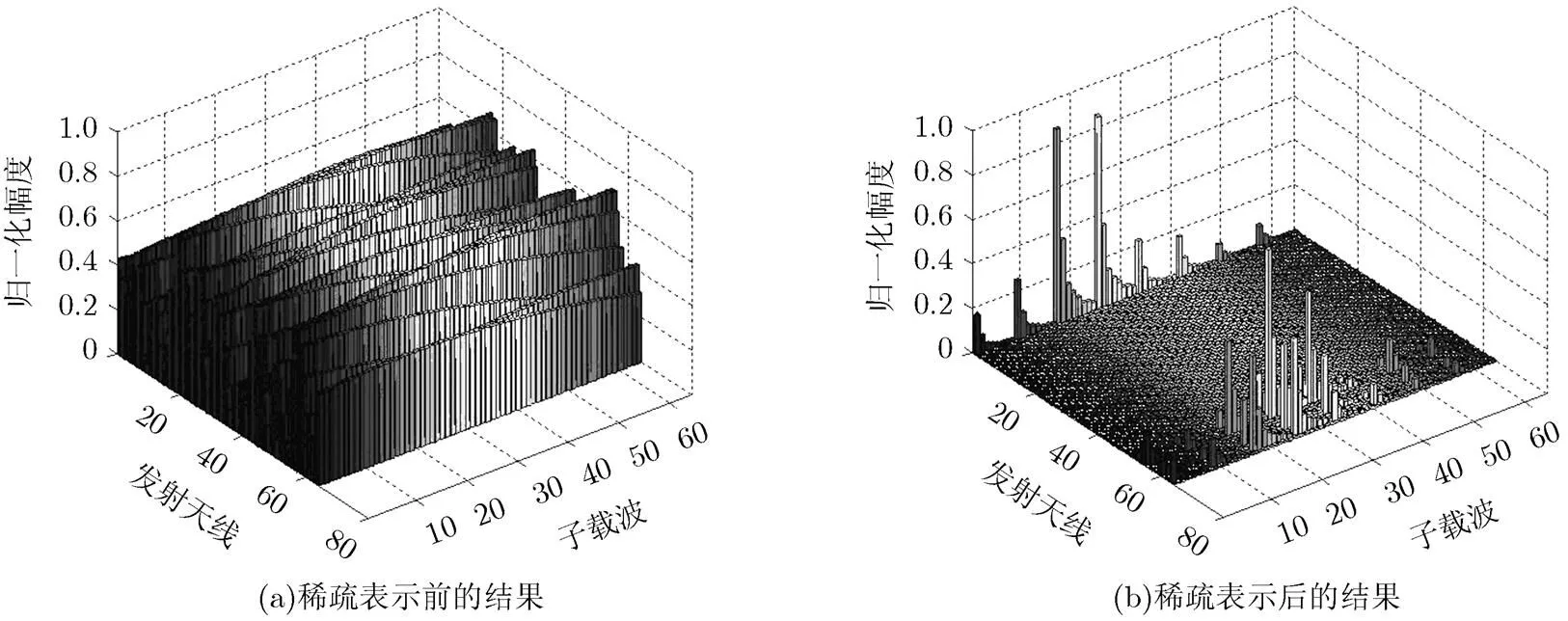
图3 稀疏表示前后信道增益直方图

图6是不同算法在相同压缩比下信道容量随信噪比变化曲线，由仿真结果可看出：本文提出的联合压缩算法的性能远远优于现有的信道稀疏算法，可获得接近于最理想反馈的性能。图7是不同算法在不同压缩比下的性能比较，可以看出，要使3种算法都获得相近的性能，本文算法需要的压缩比最小，也就是说所需要的反馈量最小。综上所述说明，本文提出的联合压缩算法可以以最低的反馈量获得接近于最理想反馈的性能。

4.2 复杂度分析

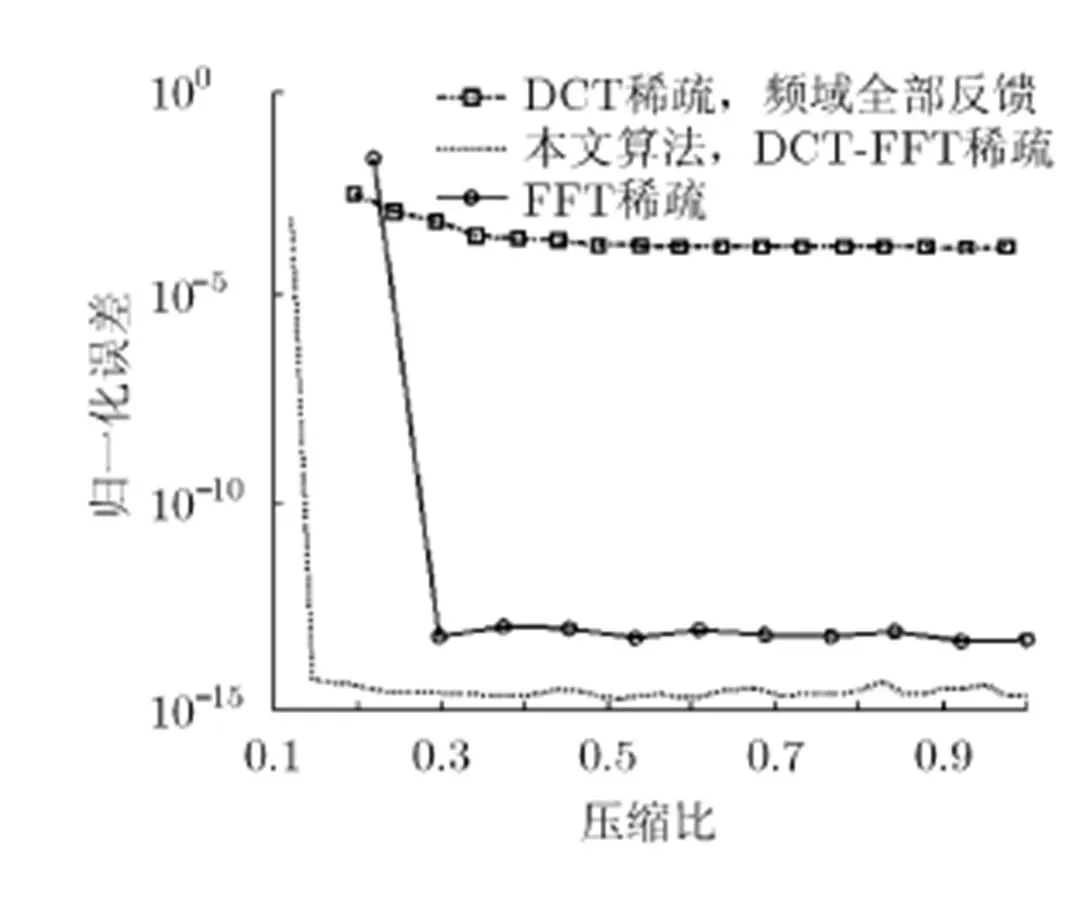
图4 不同稀疏压缩算法下的性能比较

图5 不同空间稀疏压缩算法下的性能比较

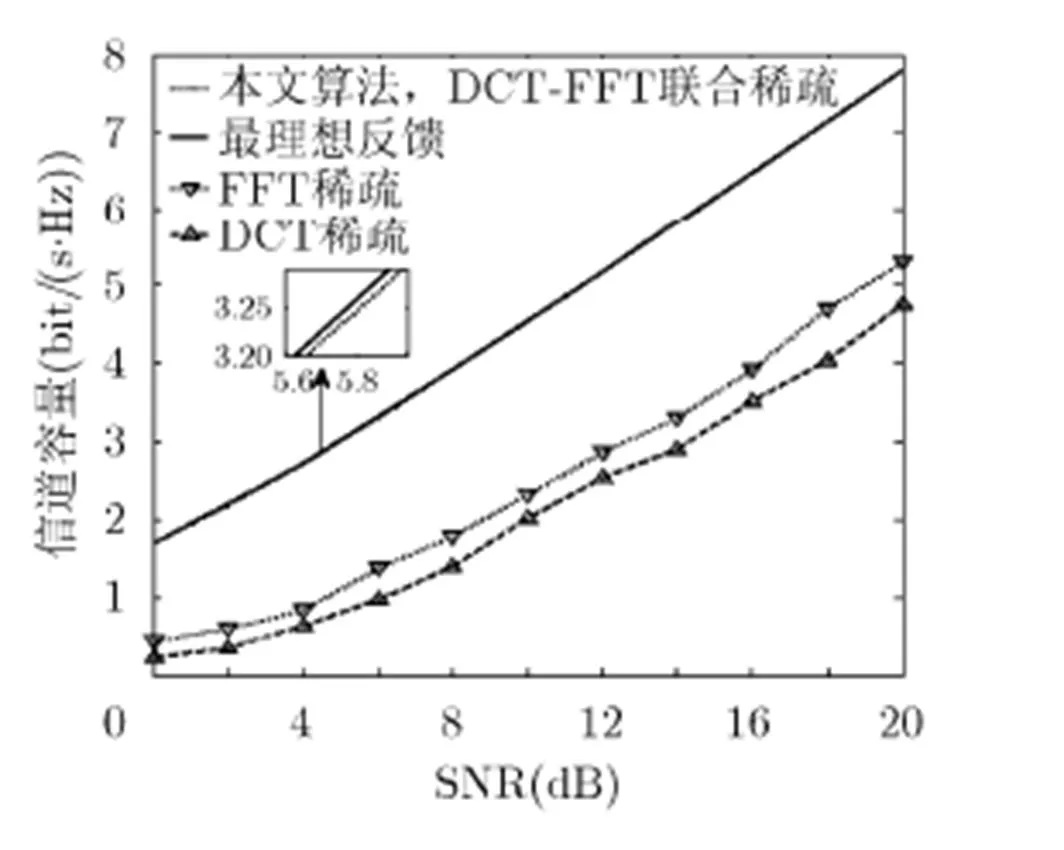
图6 不同稀疏压缩算法在相同压缩比下信道容量随信噪比变化曲线(压缩比为0.16)

图7 不同稀疏压缩算法在不同压缩比下信道容量随信噪比变化曲线

表1 不同稀疏压缩算法在接收端检测时实现复杂度(OMP迭代次数)之间的比较

5 结论

本文首先分析了大规模MIMO-OFDM系统的实际特性，介绍了现有的几种降低信道信息反馈负载的算法，并分析了这些算法的不足。然后，提出了适用于大规模MIMO-OFDM系统的基于空频相关性的联合压缩反馈算法，并推导出了相应的联合稀疏基。与仅利用空间相关性或仅利用频域相关性进行信道压缩反馈的算法相比，所提算法可在进一步降低系统反馈量的同时，以较低的复杂度保证信道信息反馈的精度。

[1] Lee Jun-ho and Lee Seung-hwan. A compressed analog feedback strategy for spatially correlated massive MIMO systems[C]. Vehicular Technology Conference (VTC Fall), Quebec City, Canada, 2012: 1-6.

[2] Kuo P, Kung H T, and Ting P. Compressive sensing based channel feedback protocols for spatially-correlated massive antenna arrays[C]. Wireless Communications and Networking Conference (WCNC), Shanghai, China, 2012: 492-497.

[3] 何雪云, 宋荣方, 周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究[J]. 南京邮电大学学报, 2010, 30(2): 60-65.

He Xue-yun, Song Rong-fang, and Zhou Ke-qin. Study of compressive sensing based sparse channel estimation in OFDM systems[J].(), 2010, 30(2): 60-65.

[4] Gao Huan-qin, Song Rong-fang, and Zhao Jun-xi. Compression of CQI feedback with compressive sensing in adaptive OFDM systems[C]. Wireless Communications and Signal Processing (WCSP), Suzhou, China, 2010: 1-4.

[5] 高欢芹, 宋荣方. 自适应 OFDM 系统中基于压缩感知的反馈压缩新方法[J]. 南京邮电大学学报, 2010, 30(3): 16-20.

Gao Huan-qin and Song Rong-fang. Compressed sensing based feedback compression in adaptive OFDM systems[J].(), 2010, 30(3): 16-20.

[6] 孙超. 基于压缩感知的无线信道信息反馈的研究[D]. [硕士论文], 南京邮电大学, 2011.

Sun Chao. Study of wireless channel state information feedback scheme based on compressed sensing[D]. [Master dissertation], Nanjing University of Posts and Telecommunications, 2011.

[7] 宋勇, 卫国. MIMO-OFDM系统的CQI反馈压缩改进算法[J].中国科学技术大学学报, 2012, 40(8): 776-782.

Song Yong and Wei Guo. An improved CQI feedback compression algorithm for MIMO-OFDM system [J]., 2012, 40(8): 776-782.

[8] 石光明, 刘丹华, 高大化. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081.

Shi Guang-ming, Liu Dan-hua, and Gao Da-hua. Advances in theory and application of compressed sensing[J]., 2009, 37(5): 1070-1081.

[9] Petersen K B and Pedersen M S. The Matrix Cookbook [OL]. http://orion.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf, 2008.

[10] 孙超, 李永杰, 宋荣方. 基于压缩感知的MIMO-OFDM系统信道状态信息反馈方案研究[J]. 南京邮电大学学报, 2012, 32(1): 54-58.

Sun Chao, Li Yong-jie, and Song Rong-fang. Study on compressed sensing based CSI feedback scheme for MIMO-OFDM systems[J].(), 2012, 32(1): 54-58.

[11] Gwon Y, Kung H T, and Vlah D. Compressive sensing with directly recoverable optimal basis and applications in spectrum sensing. Harvard Computer Science Technical Reports TR-08-11 [OL]. ftp://ftp.deas.harvard.edu/ techreports/tr-08-11.pdf, 2011.

[12] Cotter S F and Rao B D. Sparse channel estimation via matching pursuit with application to equalization[J]., 2002, 50(3): 374-377.

[13] Gwon Youngjune, Kung H T, and Vlah Dario. Compressive sensing with optimal sparsifying basis and applications in spectrum sensing[C]. Global Communications Conference (GLOBECOM),Anaheim, America, 2012: 5386-5391.

[14] He Xue-yun, Song Rong-fang, and Zhu Wei-ping. Pilot allocation for sparse channel estimation in MIMO-OFDM systems[J]., 2013, 60(9): 612-616.

[15] Vlachos Evangelos, Lalos Aris S, and Berberidis Kostas. Stochastic gradient pursuit for adaptive equalization of sparse multipath channels[J]., 2012, 2(3): 413-423.

[16] Qaseem S T, Al-Naffouri T Y, and Alghadhban S. Compressive sensing for feedback reduction in MIMO broadcast channels[C]. 17th International Conference on Telecommunications (ICT), Doha, The State of Qatar, 2010: 356-361.

[17] Kim Kiyoen, Jang Seng-hun, and Kim Dong-ku. An efficient feedback scheme using compressive sensing for MIMO broadcast channel with random beamforming[C].2nd International Conference on Computer and Automation Engineering (ICCAE),Singapore, Singapore , 2010: 743-747.

[18] Qaseem S T and Al-Naffouri T Y. Compressive sensing for reducing feedback in MIMO broadcast channels[C].IEEE International Conference on Communications (ICC),Cape Town, South Africa, 2010: 1-5.

李晓辉： 女，1972年生，教授，研究方向为宽带无线接入、无线资源管理、多天线技术.

王维猛： 男，1989年生，硕士生，研究方向为多天线技术、波束赋形及信道反馈技术.

黑永强： 男，1983年生，副教授，研究方向为MIMO及多用户MIMO、无线资源优化管理、智能进化算法及其在无线通信中的应用.

Compressed Channel Feedback Based on Spatial-frequency Correlation for Massive MIMO-OFDM Systems

Li Xiao-hui Wang Wei-meng Hei Yong-qiang

(,,’710071,)

In Massive MIMO-OFDM systems, the channel shows strong correlations in both spatial and frequency domain. Aiming at the problem that only spatial or frequency domain correlation is considered in most of the existing compressed feedback algorithms, a joint spatial-frequency compression algorithm is proposed. First, a two dimensional sparsity of channel in spatial-frequency domain is analyzed according to the compressed sensing theory. Then, a joint sparse matrix of channel is derived. Based on the joint sparse matrix, the joint spatial-frequency compression algorithm is presented. Simulation results and analysis show that, the proposed algorithm can significantly reduce the feedback load with acceptable accuracy.

Wireless Communication; MIMO-OFDM; Compressed-feedback; Spatial-frequency correlation

TN92

A

1009-5896(2014)05-1178-06

10.3724/SP.J.1146.2013.01048

李晓辉 xhli@mail.xidian.edu.cn

2013-07-17收到，2013-10-25改回

国家自然科学基金(61201135)，国家科技重大专项(2012ZX03001027-004)和高等学校学科创新引智计划资助项目(B08038)资助课题