基于约束总体最小二乘方法的到达时差到达频差无源定位算法

2014-05-30曲付勇孟祥伟

电子与信息学报 2014年5期

曲付勇孟祥伟

曲付勇孟祥伟*

(海军航空工程学院电子信息工程系烟台 264001)

两步加权最小二乘方法(two-stage WLS)是求解TDOA/FDOA无源定位问题的经典线性方法，但也存在着定位偏差和均方误差对测量噪声的适应能力较差的缺点。该文根据TDOA/FDOA的伪线性定位方程组特点，将其建立为一种带约束条件的约束总体最小二乘(CTLS)模型，并采用拉格朗日乘子法求解带约束条件的CTLS问题，建立了几种最小二乘类定位方法的统一解，从而将约束加权最小二乘(CWLS)定位解和约束最小二乘(CLS)定位解变为该文CTLS定位解的特例。仿真表明，该文方法比两步加权最小二乘方法具有更低的均方误差，并能够有效减小定位偏差，因而具有更好的测量噪声适应能力。

无源定位；到达时差；到达频差；最小二乘；偏差；均方误差

1 引言

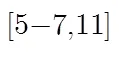
2 时差频差定位方程的描述

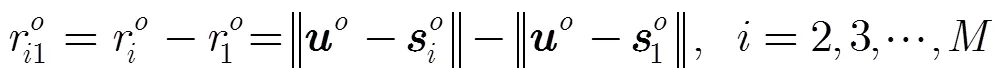
将式(1)两边求导，得到距离差变化率的公式为

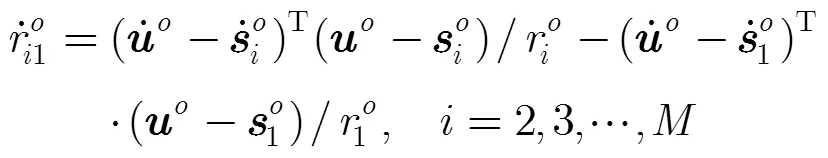
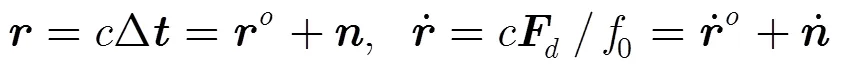
这里采用和文献[7]中一致的表达式。

3 带约束条件的CTLS定位求解

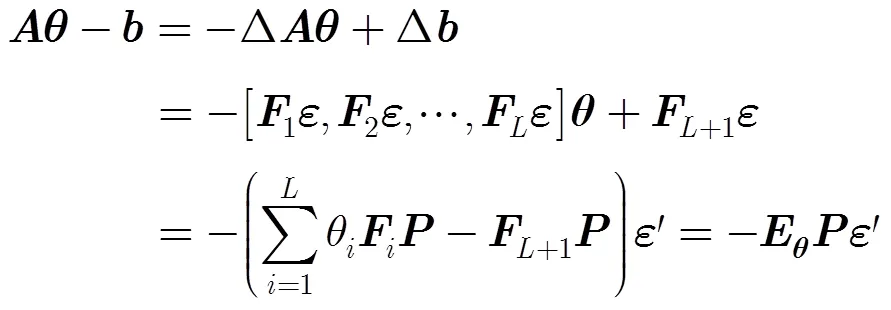
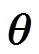
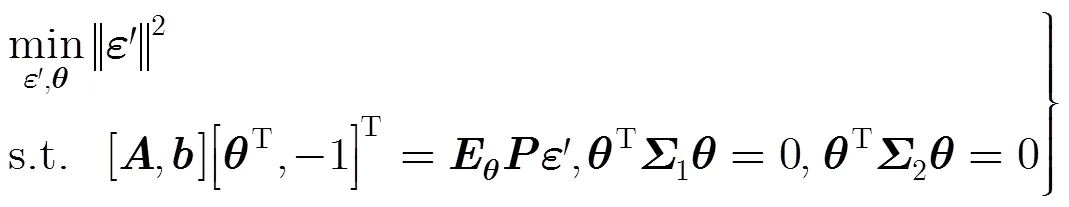
利用Lagrange乘子法，将式(9)转化为对式(10)的最小化：

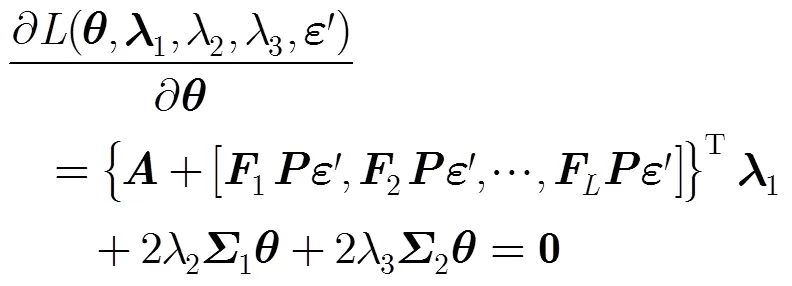
整理式(14)可得

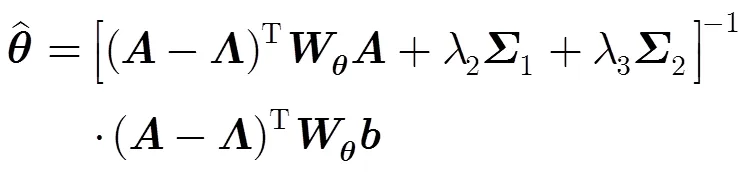
本文基于CTLS的定位算法计算过程如下：

4 讨论

(1)本文定位解与two-stage WLS的关系。two- stage WLS中给出的伪线性方程组[2]是

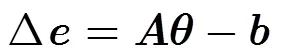
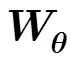
(3)文献[7]中CTLS定位解是通过极小化

5 仿真分析

图1给出了CTLS, CWLS与two-stage WLS 3种定位算法对近场源的定位位置偏差和速度偏差随接收站位置误差变化的性能曲线。由图1可以看出，CTLS方法的位置偏差和速度偏差相比two-stage WLS和CWLS都得到了显著的降低，表明CTLS方法能够有效减弱偏差的影响。

图2给出了3种定位算法对近场源的定位位置均方误差和速度均方误差随接收站位置误差变化的性能曲线。图2中，CTLS方法的位置均方误差的“门限效应”相比two-stage WLS有了明显的改善。当接收站位置误差分别大于7.5 dB, 12.5 dB时，two- stage WLS和CWLS的定位位置均方误差开始偏离CRLB，性能曲线开始发散，而CTLS方法直到大于15 dB时其位置均方误差才大于CRLB，并且随着接收站位置误差的增大，CTLS方法的位置均方误差要低于CWLS与two-stage WLS定位位置均方误差。从图2可以看出，相比位置均方误差，速度均方误差对时频差测量误差的变化更为敏感。当接收站位置误差分别大于5 dB, 7.5 dB时，two-stage WLS和CWLS的定位位置均方误差开始偏离CRLB，而CTLS方法大于10 dB时其位置均方误差才大于CRLB，并且随着接收站位置误差的增大，CTLS方法的速度均方误差要低于CWLS与two-stage WLS定位位置均方误差。

图3给出了3种定位算法对远场辐射源的位置偏差和速度偏差随接收站位置误差变化的性能曲线。显然，随着位置误差的增大，3种方法的偏差不断增大，这表明3种方法只能随接收站位置误差的减小获得渐进无偏的性能。由图3可以看出，CTLS定位方法的位置偏差和速度偏差要低于CWLS和two-stage WLS的位置偏差和速度偏差。

图1 3种算法得到的近场辐射源位置和速度偏差随接收机位置误差的变化曲线

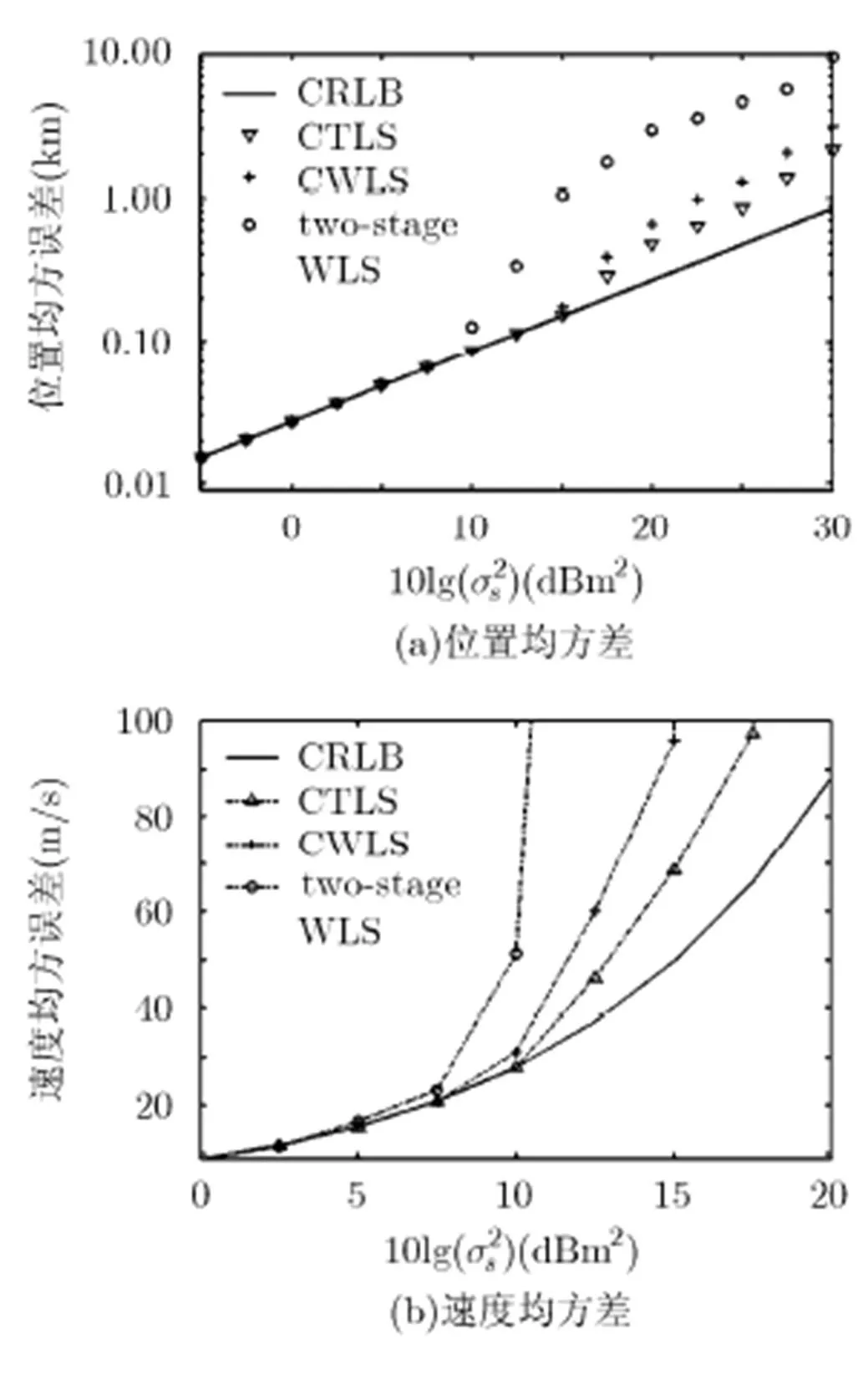
图2 3种算法得到的近场辐射源位置和速度均方误差随接收机位置误差的变化曲线

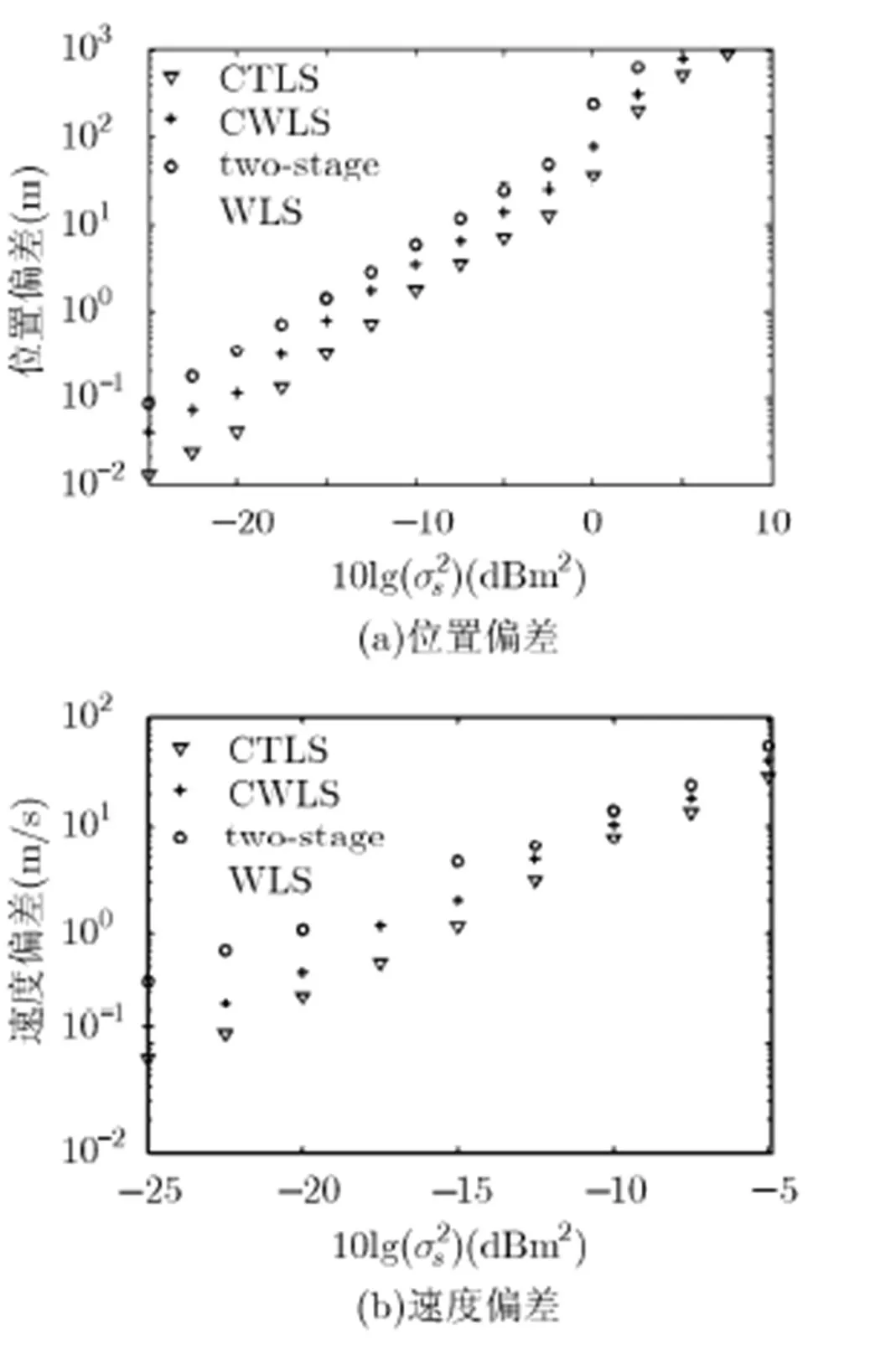
图3 3种算法得到的远场辐射源位置和速度偏差随接收机位置误差的变化曲线

图4给出了3种定位算法对远场辐射源的位置均方误差和速度均方误差随接收站位置误差变化的性能曲线，以及位置和速度的CRLB。从图4可以看出，当接收站位置误差分别大于-7.5 dB, -2.5 dB时，two-stage WLS和CWLS的定位位置均方误差开始偏离CRLB，性能曲线开始发散，而CTLS方法直到大于0 dB时其位置均方误差才大于CRLB，并且随着接收站位置误差的增大，CTLS方法的位置均方误差要低于CWLS与two-stage WLS定位位置均方误差。相比位置均方误差，速度均方误差对时频差测量误差的变化更为敏感。当接收站位置误差分别大于-20 dB, -12.5 dB时，two-stage WLS和CWLS的定位速度均方误差开始偏离CRLB，而CTLS方法直到大于-10 dB时其速度均方误差才大于CRLB，并且随着接收站位置误差的增大，CTLS方法的速度均方误差要低于CWLS与two-stage WLS定位速度均方误差。

仿真2 考察远场源中3种算法定位偏差和均方误差随时频差测量误差变化的性能。

图6给出了3种定位算法的定位位置和速度均方误差随时频差测量误差的变化曲线，以及位置和速度的CRLB。从图6可以看出，当测量误差分别大于7.5 dB, 12.5 dB时，two-stage WLS和CWLS的定位位置均方误差开始偏离CRLB，而CTLS方法直到大于15 dB时其位置均方误差才大于CRLB。相比位置均方误差，速度均方误差对时频差测量误差的变化更为敏感。当测量误差分别大于-2.5 dB, 5 dB时，two-stageWLS和CWLS的定位位置均方误差开始偏离CRLB，而CTLS方法直到大于7.5 dB时，其位置均方误差才大于CRLB。

综合分析3种方法的定位偏差和均方误差，当均方误差开始偏离CRLB时，此时估计已为有偏估计，由于CWLS方法考虑定位方程的约束关系，能够减弱其对定位偏差的影响，而本文中CTLS方法不仅考虑了约束关系，而且降低了伪线性方程中由于观测矩阵和测量向量相关导致的偏差影响，因而具有更低的偏差，且均方误差相比CWLS与two-stage WLS也得到了有效改善。

仿真3 在仿真1条件下以近场源为例，仿真本文算法的收敛性。

图4 3种算法得到的远场辐射源位置和速度均方误差随接收机位置误差的变化曲线

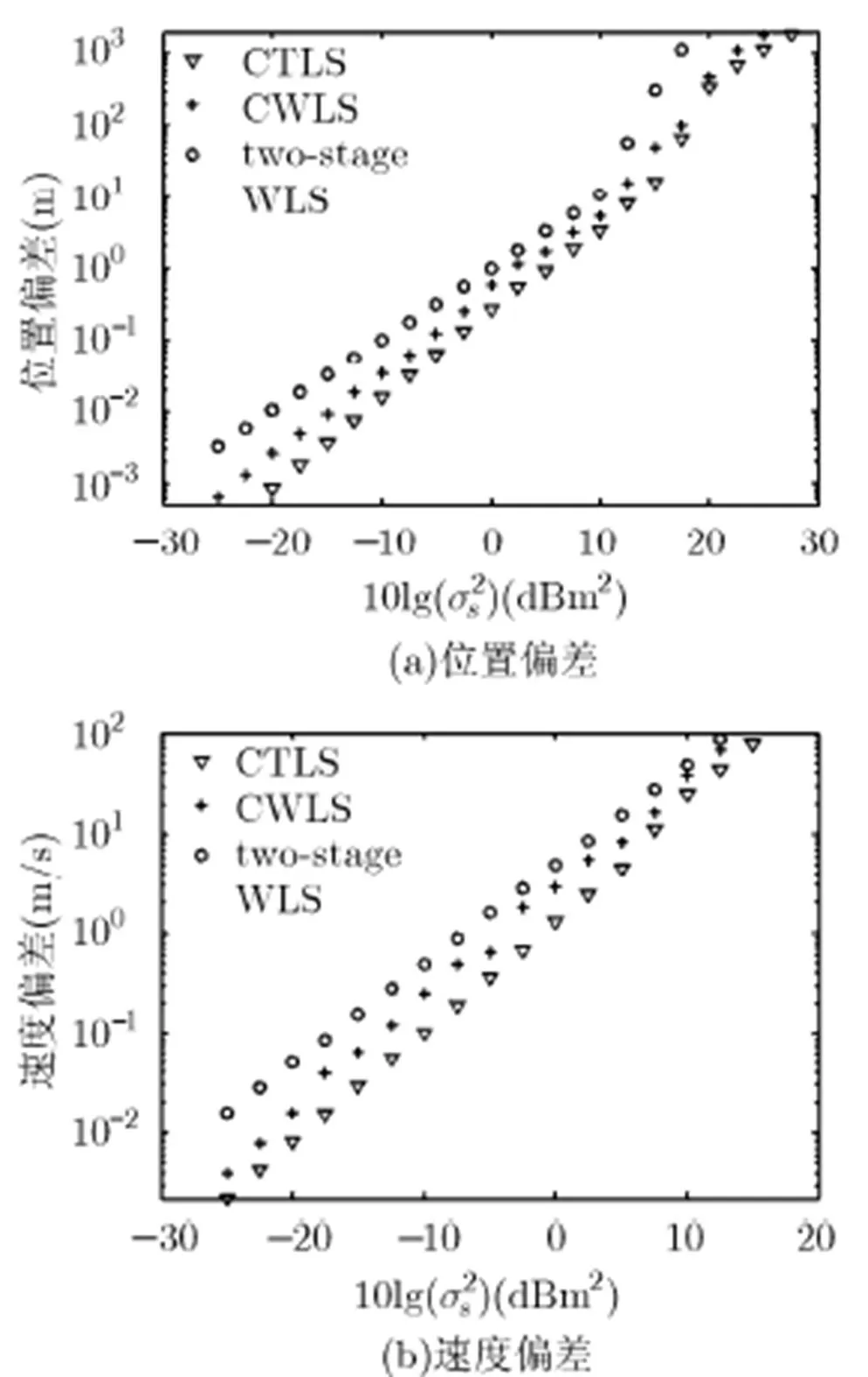
图5 3种算法得到的远场辐射源位置和速度偏差随时频差误差的变化曲线

图6 3种算法得到的远场辐射源位置和速度均方误差随时频差误差的变化曲线

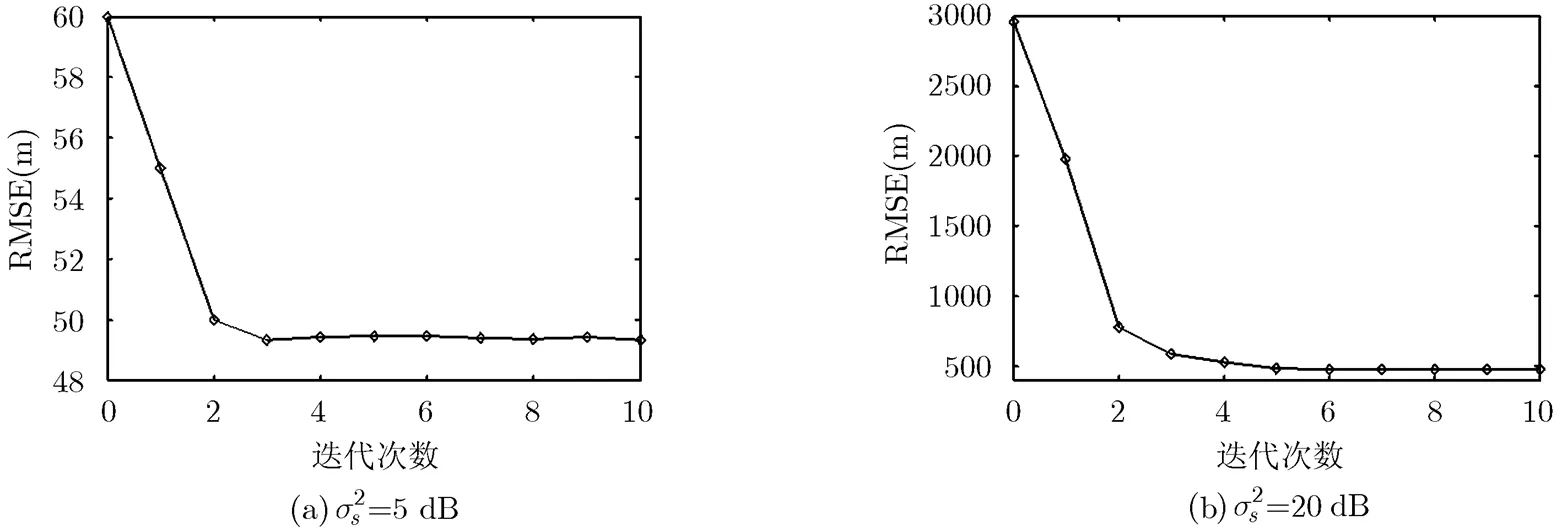
图7 本文算法得到的近场辐射源位置迭代曲线

6 结论

本文根据TDOA/FDOA伪线性方程组的特点，研究了基于约束总体最小二乘的无源定位算法。基于拉格朗日乘子法建立了几种最小二乘类定位方法的统一解，并给出了具体的求解方法。同时讨论了two-stage WLS, CWLS, CLS等定位方法解与本文定位解的关系，说明CWLS和CLS为本文定位解的特例。通过仿真表明，在时频差误差和接收机位置误差适度的条件下本文方法比two-stage WLS和CWLS方法具有更低的均方误差，并能够有效减小定位偏差，因而具有更好的测量噪声适应能力。

[1] Ho K C and Xu W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]., 2004, 52(9): 2453-2463.

[2] Ho K C, Lu X, and Kovavisaruch L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[J]., 2007, 55(2): 684-696.

[3] Sun M and Ho K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]., 2011, 59(7): 3434-3440.

[4] Sun X Y, Li J D, Huang P Y,..Total least-squares solution of active target localization using TDOA and FDOA measurements in WSN[C]. The 22th International Conference on Advanced Information Networking Applications Workshops, Okinawa, Japan, 2008: 995-999.

[5] Guo F C and Ho K C. A quadratic constraint solution method for TDOA and FDOA localization[C]. International Conference on Acoustics Speech and Signal Processing, Prague, Czech, 2011: 2588-2591.

[6] Qu F Y, Guo F C,.. Constrained location algorithms based on total least squares method using TDOA and FDOA measurements[C]. IET International Conference on Automatic Control and Artificial Intelligence, Xiamen, China, 2012: 2587-2590.

[7] Yu H, Huang G, and Gao J. Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J].,&, 2012, 6(9): 891-899.

[8] Ho K C. Bias reduction for an explicit solution of source localization using TDOA[J]., 2012, 60(5): 2101-2114.

[9] Xu B, Qi W D, Wei L,.. Turbo-TSWLS: enhanced two-step weighted least squares estimator for TDOA-based Localisation[J]., 2012, 48(25): 1597-1598.

[10] Amar A, Leus G, and Friedlander B. Emitter localization given time delay and frequency shift measurements[J]., 2012, 48(2): 1826-1837.

[11] Cheung K W, So H C,.. A constrained least squares approach to mobile positioning: algorithms and optimality[J]., 2006: 1-23.

[12] Yu H, Huang G, Gao J,..Practical constrained least-square algorithm for moving source location using TDOA and FDOA measurements[J]., 2012, 23(4): 488-494.

[13] Stoica P and Li J. Source localization from range-difference measurements[J]., 2006, 23(6): 63-65.

[14] Abatzoglou T J, Mendel J M, and Harada G A. The constrained total least squares technique and its applications to harmonic superresolution[J]., 1991, 39(5): 1070-1087.

[15] Schaffrin B. A note on constrained total least-squares estimation[J]., 2006, 417: 245-258.

[16] Foy W H. Position-location solutions by Taylor-series estimation[J]., 1976, 12(2): 187-194.

曲付勇：男，1984年生，博士生，研究方向为无源定位、数据压缩.

孟祥伟：男，1966年生，教授，博士生导师，研究方向为雷达信号检测、信号理论、定位等.

Source Localization Using TDOA and FDOA MeasurementsBased on Constrained Total Least Squares Algorithm

Qu Fu-yong Meng Xiang-wei

(,,264001,)

The two-stage Weighted Least Squares (WLS) method is a well-known linear approach in Time- Difference-Of-Arrival (TDOA) and Frequency-Difference-Of-Arrival (FDOA) passive localization. But this method can only attain the CRLB in a modest noise environment and the bias of the localization result is significant for strong noise. This paper discusses a Constrained Total Least Square (CTLS) solution to the pseudo linear equations with two constrains for TDOA/FDOA localization. A unified expression for several LS solutions is derived based on Lagrange multiplier. The Constrained Weighted Least Square (CWLS) method and Constrained Least Square (CLS) localization method reduce to the special cases of the localization solution. The simulation results show that the proposed method has lower Mean Square Error (MSE) and lower bias compared with the two-stage WLS method, and it is more robust to noise.

Passive localization; Time-Difference-Of-Arrival (TDOA); Frequency-Difference-Of-Arrival (FDOA); Least Square (LS); Bias; Mean Square Error (MSE)

TN971

1009-5896(2014)05-1075-07

10.3724/SP.J.1146.2013.01019

孟祥伟 mengxw163@163.com

2013-07-11收到，2013-11-26改回

国家自然科学基金(61179016)资助课题