基于抱箍吊装技术的大吨位薄壁筒屈曲稳定性研究*

2014-05-29谢大帅黄松和杨高传

化工机械 2014年4期

谢大帅黄松和杨高传

(1. 西南交通大学机械工程学院；2. 中铁四局集团有限公司工管中心)

在化工行业中，对一些无吊装吊耳或顶层吊盖的薄壁筒(如吸收塔、造粒塔等)常采用摩擦抱箍法进行吊装。薄壁筒在使用抱箍吊装时不仅受到来自箍身均匀的外压载荷，而且受到来自牛腿因偏载力产生的局部外压载荷，对于直径与厚度比大于20的薄壁圆筒来说，在外压载荷下容易周向屈曲失稳[1]。而随着科技的发展，吸收塔、造粒塔等化工设备正向着高产能、大直径、大吨位的方向发展，因此传统的单抱箍结构已不能满足吊装要求。为了满足大吨位、大直径薄壁筒吊装的要求，提出了一种新型的双抱箍结构，通过对单、双抱箍作用下薄壁筒的受力进行分析，推导出了薄壁筒稳定性计算公式，并通过300t硝酸吸收塔吊装实例用有限元的方法加以验证。通过对比分析表明：双抱箍结构在大吨位薄壁筒的吊装施工工艺中具有较大优势，为大吨位薄壁筒的吊装提供新思路。

1 摩擦抱箍法

图1为传统的单抱箍结构示意图。抱箍主要结构为两个折弯成略小于半圆形的钢板，钢板上焊接有箱型结构的牛腿和预紧螺栓板。通过预紧螺栓使两半圆形钢板对薄壁筒产生正压力，从而产生克服竖向载荷的摩擦力。

图1 单抱箍结构示意图

图2为双抱箍的结构示意图。双抱箍由上、下两个单抱箍组成，上、下抱箍的牛腿通过连接梁由抗摩擦型高强度螺栓组连接。单个抱箍的宽度小便于加工，而且在运输时可将上、下抱箍和连接梁拆卸便于运输。

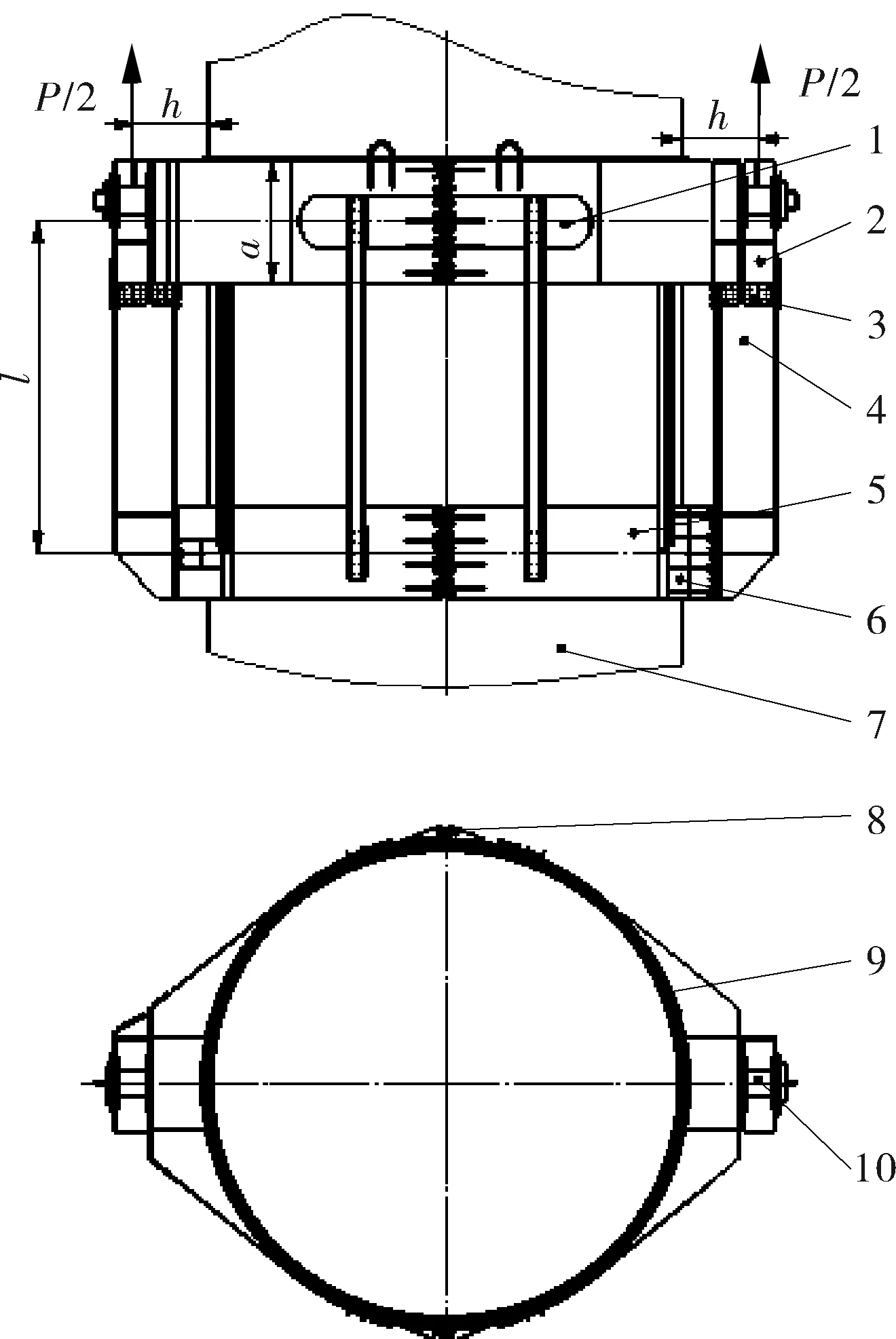
图2 双抱箍结构示意图

2 稳定性计算公式推导

2.1单抱箍作用下薄壁筒稳定性计算公式

薄壁筒在抱箍吊装时,一方面受到来自箍身抱紧薄壁筒产生的外压,可近似认为这种外压力沿周向均匀分布[2]，对薄壁筒稳定性影响不大。另一方面如图1、2所示，作用在牛腿上的竖向载荷由于距牛腿根部有一定的距离h形成偏载，偏载的竖向力会产生较大的弯矩，从而对薄壁筒表面产生较大的局部外压，是引起薄壁筒失稳的主要原因。因此在计算抱箍作用下薄壁筒屈曲稳定性时，可以只考虑来自牛腿的局部外压作用。

对于单抱箍牛腿可以将其简化为简支梁模型，在单边竖向力的作用下所产生的弯矩为：

(1)

式中h——竖向力作用点到牛腿根部的距离；

P——吊装时所需克服的竖向载荷。

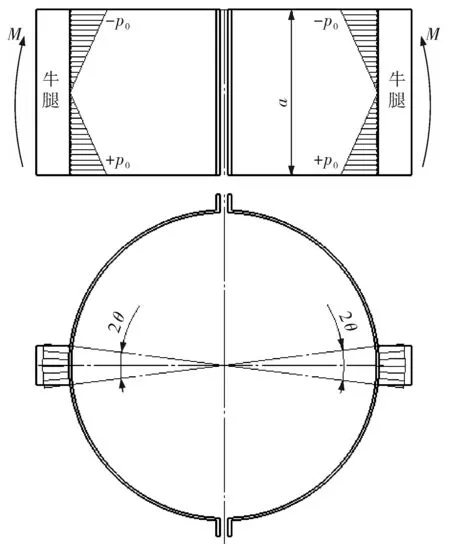
图3 单抱箍牛腿在箍身上的应力分布

由于抱箍的厚度相对于其直径尺寸较小，可将抱箍视为柔性弹体[3]，作用在抱箍上的压应力可认为直接作用在薄壁筒上。因此可将薄壁筒的受力看作两段沿周向相距很远的间断式集中外压载荷，如图4所示。载荷的平均值pd为：

(2)

当在壳的一段上沿周向受均匀分布的压力作用时，其临界外压载荷pkp为[4]：

(3)

式中a——外压载荷作用宽度；

E——薄壁筒材料的弹性模量；

k——薄壁筒的形状缺陷系数，由于此处载荷为两段沿周向相距很远的间断式集中外压载荷，因此k值可取为0.5；

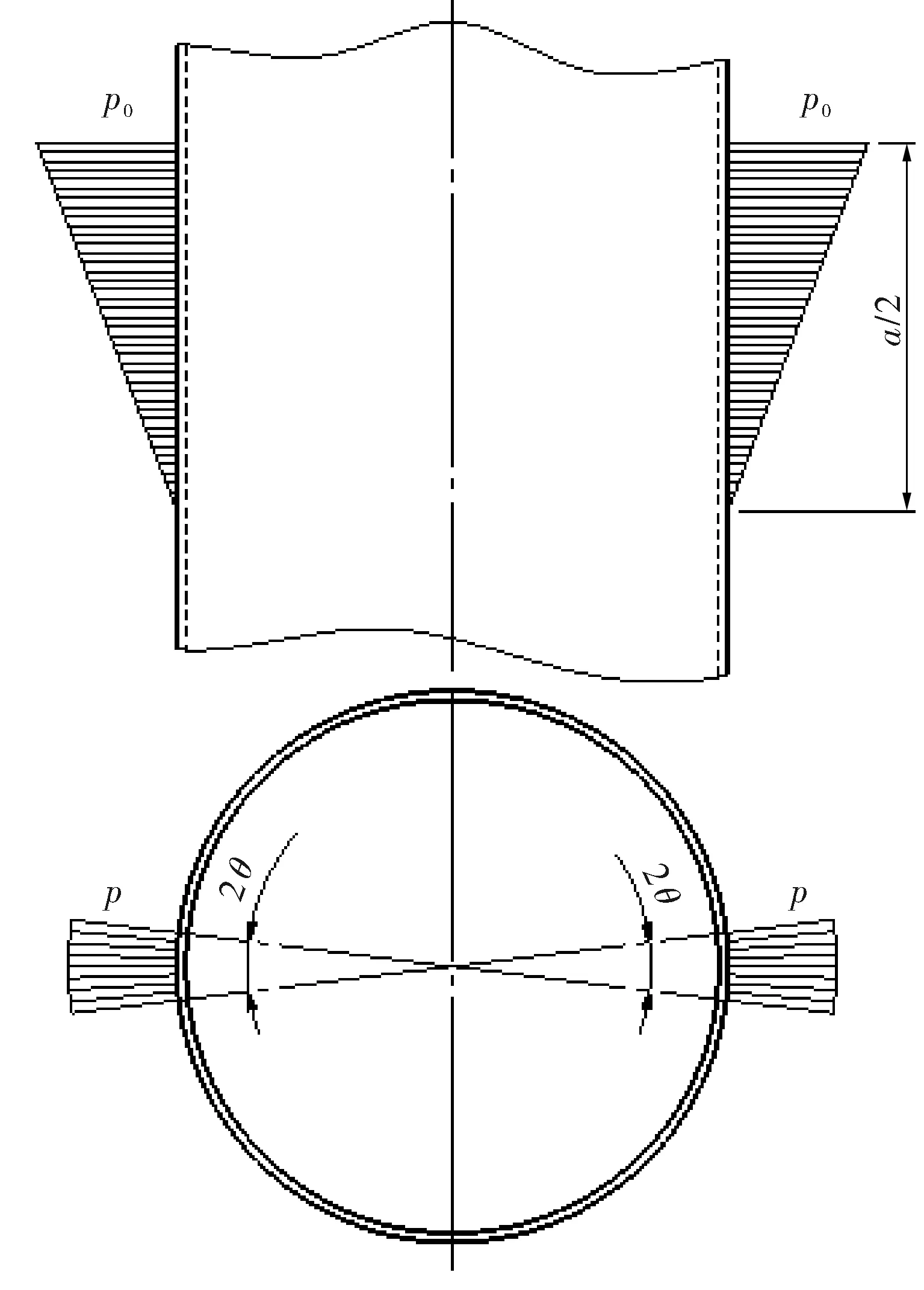
图4 单抱箍牛腿在薄壁筒上的应力分布

pkp——周向临界外压载荷；

R——薄壁筒的半径；

α——和约束有关的系数，此处由于抱箍的宽度相对于薄壁筒长度较小，α可取0.5；

δ——薄壁筒的厚度。

单抱箍作用下要使薄壁筒不屈曲失稳，应满足：

pd≤pkp

(4)

由式(1)～(4)可以求得薄壁筒不失稳的情况下单抱箍所能承受的最大竖向力为：

(5)

式中Pd——单抱箍所能承受的最大竖向力。

2.2双抱箍作用下稳定性计算

对于双抱箍结构，上、下抱箍的牛腿与连接梁之间的连接可视为刚性，组成一门架结构。由于上、下抱箍与薄壁筒间垫有橡胶层，使得抱箍与薄壁筒之间允许有一定的转动，且在竖向力的作用下使抱箍和薄壁筒有分离趋势，下抱箍与薄壁筒之间没有较大的摩擦力作用，因此下抱箍可以简化为移动铰支座。而上抱箍对薄壁筒有正压力作用且产生了较大的摩擦力来克服起吊力，可以将上抱箍处牛腿简化为固定铰支座。因此双抱箍吊装的力学模型可简化如图5a所示的静定门架式结构，其受力分析如图5b所示。

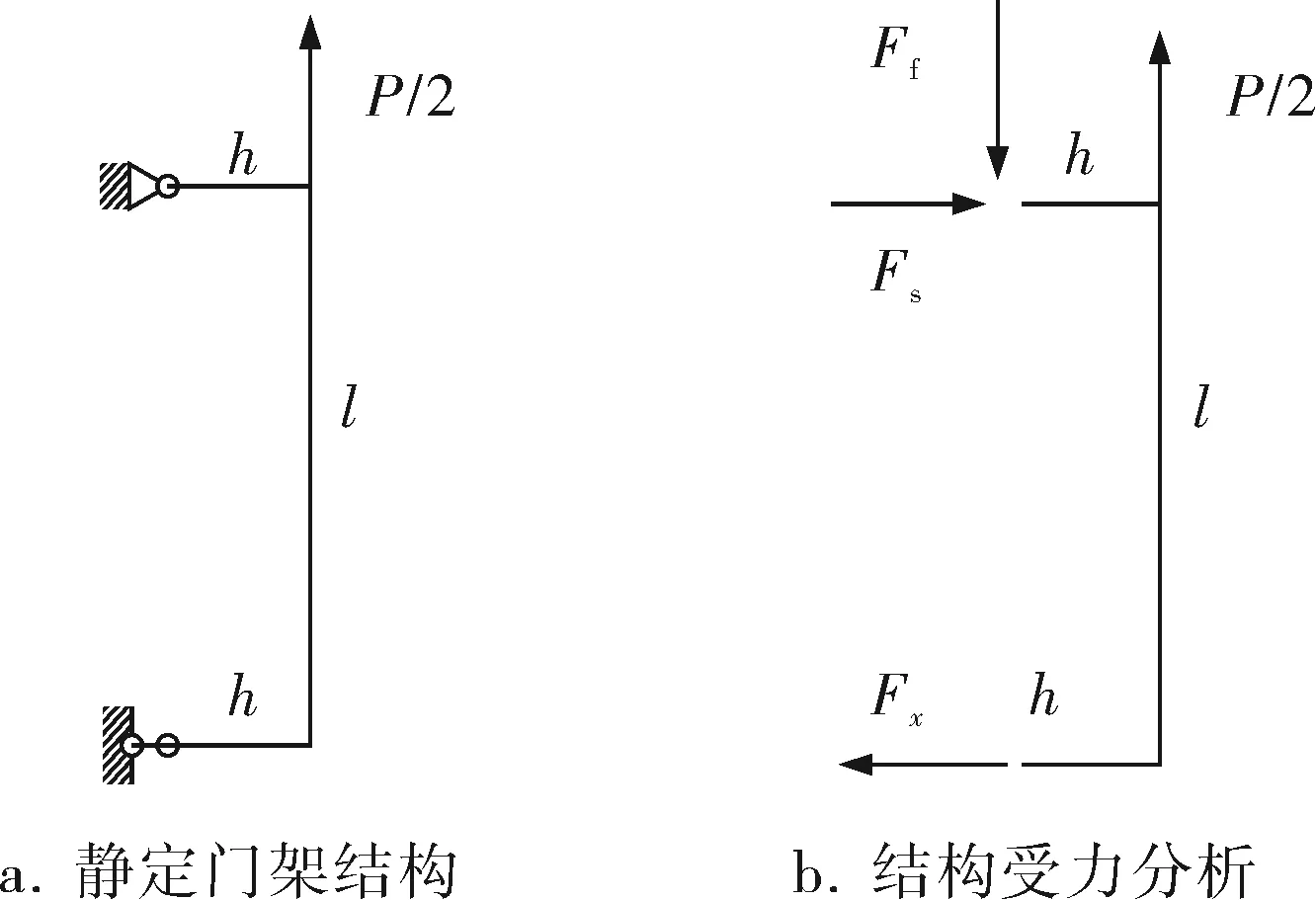
图5 双抱箍牛腿简化模型

根据力学平衡原理，可以求出上抱箍牛腿与箍身之间的作用力：

(6)

式中Fs——上抱箍牛腿处的支反力；

l——上下抱箍宽度中心的距离。

由于牛腿作用在箍身上的力可近似认为作用在薄壁筒上，因此薄壁筒的应力分布仍可看成是沿周向分布的两段相距很远的集中外压载荷。因此牛腿在薄壁筒表面产生的正压力平均值ps为：

(7)

式中as——双抱箍结构的上抱箍宽度。

要使薄壁筒在双抱箍作用下不发生屈曲失稳，应满足：

ps≤pkp

(8)

由式(1)、(6)、(7)、(8)可以得出在双抱箍作用下，薄壁筒所能承受的最大竖向力：

(9)

由式(5)、(9)可以看出，当薄壁筒结构和尺寸确定时能够影响薄壁筒稳定性的尺寸参数有竖向力距牛腿根部的距离h、抱箍宽度a、两抱箍之间的距离l和抱箍的周向作用范围2θ。对于单抱箍而言，尺寸参数有竖向力距牛腿根部的距离h和抱箍的周向作用范围θ，因为结构自身的原因无法做出大范围调整。要想提高单抱箍作用下的薄壁筒的稳定性就必须增加抱箍的宽度，但这样势必增加了加工运输的难度和成本，因此单抱箍吊装时其承载能力有限。而对于双抱箍而言，在其他条件都一样的情况下其吊装能力是单抱箍的3～4倍，而且可以通过增加上下抱箍间的距离来提高承载能力。因此抱箍在薄壁筒吊装作业中具有很大的优势。

3 有限元算例验证

3.1公式计算结果

某化工公司总质量为275t的硝酸吸收塔采用双抱箍法成功吊装。吸收塔塔体和所设计抱箍的相关尺寸如下：

硝酸吸收塔质量 275t

吸收塔壁厚δ25mm

吸收塔总长L57m

吸收塔外径R4.5m

弹性模量E2.1GPa

上抱箍宽度 1.4m

下抱箍宽度 1.3m

上、下抱箍中线间距离l3.2m

吊点距牛腿根部距离h0.65m

抱箍周向作用范围2θ19rad

抱箍厚度 20mm

抱箍外径 4.469m

抱箍自重 15.5t

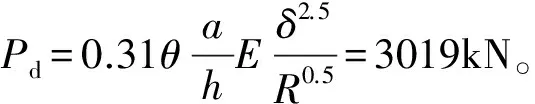
可以看出若采用单抱箍吊装，将抱箍宽度设计为双抱箍上、下抱箍的宽度和仍不能满足吊装要求。要使单抱箍达到双抱箍的吊装能力，须将单抱箍的宽度增加到约9.6m，这样会给抱箍的加工和运输带来很大的难度。

3.2有限元验证

ANSYS有限元分析软件有专门的分析计算模块分析结构承受外压时的屈曲状况，即特征值屈曲分析[5]，其分析过程为：首先建立有限元模型，对模型施加一极小的单位载荷进行一般静力分析；然后退出静力分析求解器，进入屈曲分析求解器进行屈曲分析；最后对计算结果进行模态扩展求得屈曲时的失稳模态频率和失稳形态。所求得的失稳模态频率乘以单位载荷即模型失稳时的临界载荷。

3.2.1有限元模型简化

屈曲稳定性分析主要是针对吸收塔自身进行分析，为了节约内存空间和计算时间，可将抱箍的牛腿和连接梁简化为箱梁结构，且当薄壁筒计算长度较长时可忽略薄壁筒两端封头等部件的约束作用[6]。简化后的模型如图6所示。

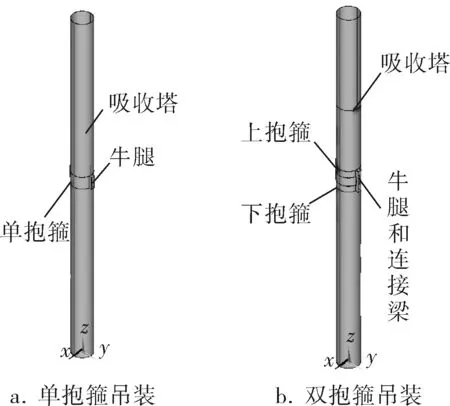
图6 抱箍简化模型

3.2.2计算结果

将吸收塔底面全约束，在模型预紧螺栓板位置处施加单位的面载荷作为螺栓预紧力，相应施加的单位竖向力为101.74kN进行屈曲分析。得到的屈曲系数λd=32.25、λs=108.75，相应地求出单、双抱箍吊装时薄壁筒不屈曲失稳时的最大竖向载荷Pd′=λd×101.74=3281.1kN、Ps′=λs×101.74=11064kN，单、双抱箍作用下薄壁筒屈曲模态如图7所示。