底部约束变化对搁置状态下整体爬升式钢平台安全性能的影响分析
2020-08-07吴水根汪小林
吴水根 高 茁 张 铭 汪小林
1. 同济大学建筑设计研究院(集团)有限公司 上海 200092;
2. 同济大学土木工程学院 上海 200092;3. 上海建工四建集团有限公司 上海 201103
近年来,整体爬升式钢平台模架体系在国内各地区的超高层项目中均被广泛应用[1-2],其根据混凝土核心筒结构的特点,选择爬升系统及支撑系统,因构造简单、受力明确、装拆方便等特点而广受欢迎。此类钢平台在工作工况下的竖向荷载由钢平台底部钢梁的竖向限位装置——钢牛腿传递到核心筒中的牛腿预埋盒上;钢平台所受水平荷载主要由布置于底部钢梁外侧的水平限位装置——顶墙导轮承担。此钢牛腿与顶墙导轮一同构成了钢平台工作工况下的底部约束系统。作为模架与主体结构之间的传力构件,二者所受的荷载相对钢平台其他构件较大,并易因牛腿预埋盒施工误差、适应墙体收分所产生的牛腿伸长、侧向位移及施工误差作用下部分顶墙导轮脱开等因素,使得计算结果与实际情况有所差异,在极端情况下甚至会出现局部牛腿预埋盒附近的混凝土压碎、牛腿与牛腿预埋盒脱开、大量顶墙导轮不工作等不利情况。
目前,有关整体爬升钢平台模架体系的研究有施工技术的应用及理论计算等。在理论计算中,文献[3]定性地验证了某实际项目使用的钢平台安全性能;文献[4]给出了一种建立钢牛腿及附属构件的有限元建模方法,并得到了单个牛腿所能承受的最大荷载;文献[5]计算并得出了钢平台抗侧刚度的参考值。参考上述文献中的理论计算方法,本文主要研究钢平台底部约束系统在实际工作工况下的受力状态及安全储备。通过建立钢平台简化及精细化有限元模型,模拟工作工况下钢平台底部约束的受力情况,并采用参数化分析方法,以牛腿底部标高、牛腿伸长量、顶墙导轮的脱开数量等为参数,定性及定量地讨论钢平台底部约束的安全性能,最后提出在危险荷载组合作用下,钢平台底部约束的加固措施,为后续钢平台的应用提供参考。
1 搁置状态下整体爬升式钢平台底部约束体系
整体爬升式钢平台模架体系采用钢柱-筒架交替支撑的方式进行施工及爬升。该模架体系(图1)主要有4个部分:顶部钢平台系统,作施工作业平台;内外挂脚手系统,作核心筒混凝土的施工脚手架;钢柱爬升系统,为钢平台的爬升提供动力;筒架支撑系统,包括竖向支撑限位装置(牛腿)、水平支撑限位装置(顶墙导轮)等(图2),在钢平台体系施工作业状态提供支撑作用,通过其上设置的竖向支撑限位装置与水平限位支撑装置分别将钢平台体系承受的竖向荷载、水平荷载传递给混凝土结构。
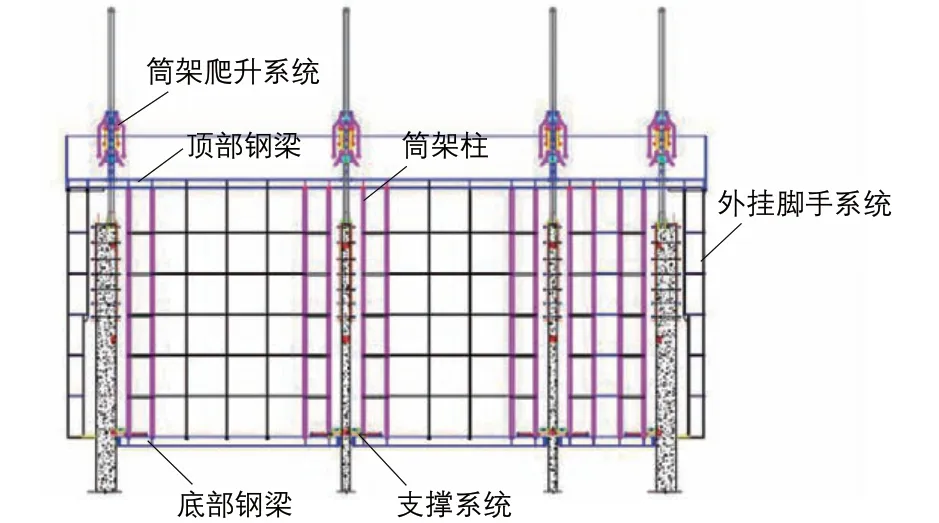
图1 钢平台体系示意

图2 钢平台牛腿、顶墙导轮示意
工作工况下,位于钢平台底部的钢牛腿伸出并搁置在核心筒中的牛腿预埋盒上。此时牛腿承担钢平台的竖向荷载,当钢平台受到侧向风荷载或活荷载作用产生水平变形时,位于底部钢梁处的顶墙导轮与墙面接触,将水平荷载直接传递给核心筒混凝土并限制钢平台的水平变形。此工况下,钢平台各组成部分所受荷载为:钢平台系统受钢筋堆载、钢大模荷载、施工活荷载、顶部吊车梁荷载、设备荷载等;外挂脚手架受风荷载、施工活荷载;钢柱爬升系统不受荷;筒架支撑系统提供水平及竖向抗力。钢平台模架荷载传递路径如图3所示。

图3 钢平台竖向及水平向荷载传导示意
2 有限元建模及各工况的分析参数
2.1 模型建立
以某在建超高层项目为研究对象,结构高243.55 m,其采用的施工钢平台共6层,顶面作业面积870 m2。采用建筑领域通用结构分析及设计系统软件Midas Gen建立此钢平台的有限元简化模型及精细化模型:其中简化模型用于模拟钢平台整体在各施工荷载作用下的受力情况;精细化模型用于模拟钢牛腿在各特殊荷载工况下的应力状态。
简化模型中,钢平台钢梁、内外挂脚手均采用Midas梁单元进行模拟;钢梁及筒架柱采用Q345钢,内外挂脚手架采用Q235钢;钢平台底部水平约束(顶墙导轮)采用只压弹簧支座进行模拟,弹簧刚度取200 kN/mm,竖向约束(牛腿)采用限制竖向位移的固端约束模拟。水平及竖向约束的布置如图4所示。
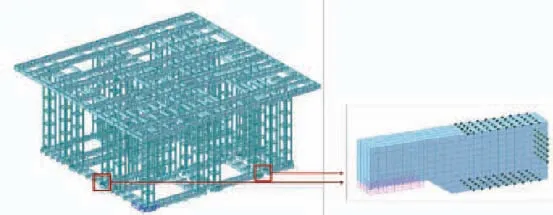
图4 钢平台简化模型、精细化牛腿模型及其约束布置
精细化模型中,钢平台牛腿采用实体单元进行模拟,材料为Q345钢。在整体模型中,用实体单元牛腿替换掉简化模型中相应位置的竖向约束,并将牛腿底部与钢梁连接的部位用刚性约束进行简化。
2.2 水平约束数值模拟方案
在实际工程中,通过对顶墙导轮的监测发现,钢平台在风荷载、安装误差等因素的作用下,并非全部顶墙导轮均与墙面接触。因此,定义顶墙导轮约束状态为基本参数,参考施工中的实际接触状况,将顶墙导轮在x向来风下的工作状态按接触类型分为如下3类:钢平台在风荷载作用下产生倾斜,导致同x坐标的所有顶墙导轮不工作;筒与筒间仅通过顶部钢梁连接,筒间存在相对位移,导致同x坐标但不同筒内的顶墙导轮不工作;筒架内部扭转,导致某筒内同x坐标的部分顶墙导轮不工作。由于采用x负向的风荷载进行计算,因此钢平台产生向左的位移,假定只有筒右侧的顶墙导轮脱开,可得表1所示的荷载组合。分析中风荷载等级取8级,牛腿及顶墙导轮布置如图5所示。
2.3 竖向约束数值模拟方案
钢平台牛腿在牛腿搁置误差、墙体收分等因素影响下,初始标高及伸长量均有差异,因此以二者为参数对牛腿约束状态进行分析。
1)由于钢平台牛腿数量众多,为探究钢牛腿使用极限,需根据钢平台在初始状态下的牛腿反力分布状态,根据牛腿分布位置、初始反力等将钢平台牛腿进行分组计算。此外,受温度变化、混凝土收缩等因素影响,牛腿预埋件的高度精度控制范围在5 mm左右,因此模拟中需以5 mm作为初始位移增量并在此基础上进行调整。

表1 水平约束取值工况及荷载组合
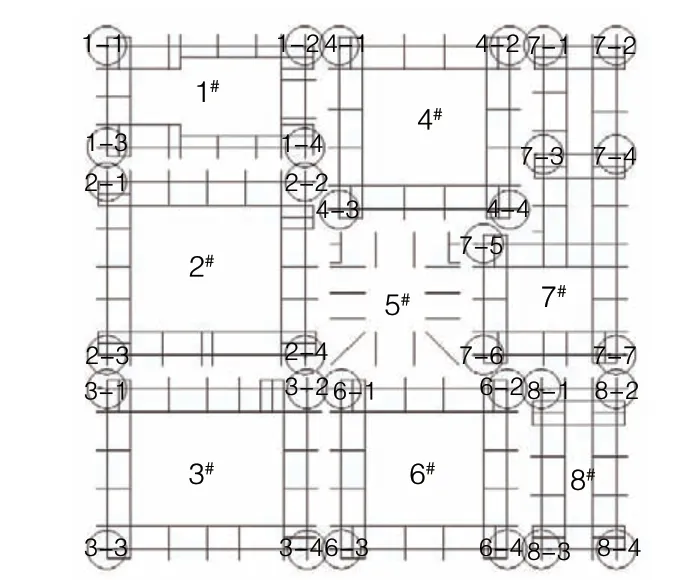
图5 牛腿及顶墙导轮布置示意
2)在实际工程中,核心筒结构墙体收分仅对部分搁置于内墙的牛腿产生伸长量的影响,此类牛腿编号包括1-2、1-4、2-2、2-4、3-1、3-2、3-4、4-3、4-4、6-1、6-2、7-1、7-3、8-1、8-3。由于墙体收分以50 mm为一段工况,由400 mm收缩至200 mm,故取以50 mm为增量的50~200 mm总计5种工况对钢平台牛腿的伸长量进行定性研究,分别调整精细化模型中的牛腿伸长量;并除上述5种工况外,在230 mm的基础上以50 mm为增量继续收缩墙体直至钢牛腿应力极限,以牛腿初始应力为参数,定量分析此极限的工况下,不同初始应力等级的牛腿伸长量限值。
3 底部约束有限元计算结果与参数化分析
3.1 顶墙导轮接触状态影响分析
将2.2节所述3种荷载工况带入有限元模型中进行计算,从顶墙导轮反力、牛腿反力、钢平台倾斜率及层间位移4个方面定性地分析水平约束对钢平台安全性能的影响。
3.1.1 顶墙导轮反力
计算9种组合可得:顶墙导轮反力最大值发生在编号1-2顶墙导轮,大小为14 kN,此时1#~3#筒迎风向仅有编号1-2顶墙导轮顶上,结合反力及实际情况,此时为顶墙导轮工作的最不利工况(图6)。
由奇数号顶墙导轮反力变化曲线可知,随着偶数号顶墙导轮逐渐退出工作,其反力呈现减小的趋势,但变化数值较小,总变化仅为6%;而偶数号未退出工作的顶墙导轮反力变化较大,且当相邻偶数号顶墙导轮退出工作时,其反力达到最大。因此,当筒内出现某一顶墙导轮脱开时,需重点关注其相邻偶数号顶墙导轮的工作状态。
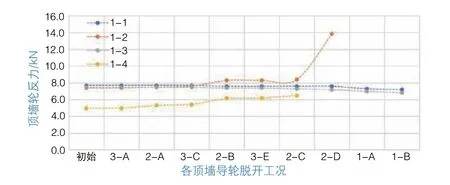
图6 1#筒顶墙导轮反力-工况示意
3.1.2 筒架柱整体倾斜率
筒架柱整体倾斜率中,取顶部钢平台钢梁底面至底部钢梁顶面为计算长度,用以表述钢平台在水平荷载及位移作用下的倾斜程度。图7为钢平台3#筒的倾斜率-工况变化曲线。相较初始状态,顶墙导轮脱开后钢平台的倾斜率由0.06%增大到0.12%,增大100%。在实际工程中,倾斜率变化与极端风荷载作用下,钢平台产生的倾斜率变化在数量级上保持一致。因此,此工况较为不利,在施工中需重点关注顶墙导轮脱开时筒架柱的倾斜率。
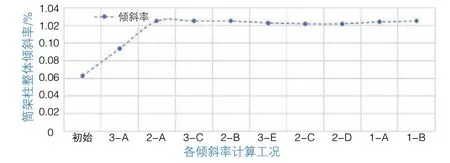
图7 3#筒倾斜率-工况示意
3.1.3 钢平台层间位移
在3#筒层间位移变化工况下,钢平台筒架柱产生最大为3.5 mm的层间位移,其位移值小于JGJ 459—2019《整体爬升钢平台技术标准》中规定的9 mm限值。由初始工况至1-B工况,层间位移增大1.5 mm,相较2.0 mm的初始层间位移较大。因此,在分析钢平台层间位移变化时,需考虑顶墙导轮的工作状态(图8)。
3.1.4 牛腿反力
由1#~3#筒钢平台牛腿反力变化数据可知,相较顶墙导轮反力,牛腿反力变化较小,其变化值在3%以内,由于顶墙导轮退出工作,导致部分由风荷载产生的弯矩改为由牛腿承担,因此牛腿反力的变化趋势为同一筒架内偶数号牛腿反力减小,奇数号牛腿反力增大(表2)。
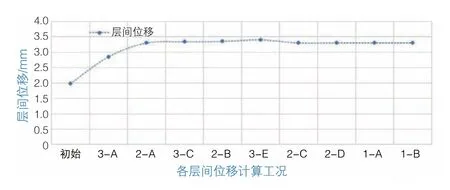
图8 钢平台层间位移-工况示意
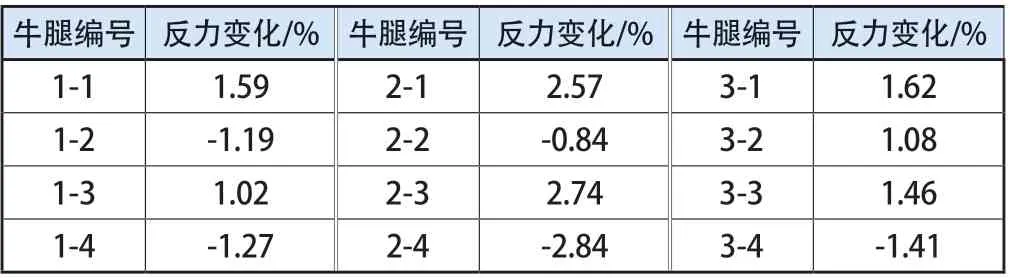
表2 牛腿反力
3.2 牛腿约束状态影响分析
由钢平台简化模型与精细化模型计算得牛腿反力对比的情况可知,二者在各牛腿上产生的反力差值在2%以内,因此可认为二者的计算结果基本一致并可进行对比。
采用精细化模型计算结果进行分析,钢平台在施工荷载作用下,其角部牛腿反力达500 kN以上,而内侧筒牛腿反力在350 kN左右,因此可将牛腿分为角部筒(1#、3#、8#)牛腿及内侧筒(2#、4#、6#)牛腿,并以牛腿初始反力为参数,分别计算200、250、300、350、500 kN级牛腿的初始标高差异限值。
3.2.1 角部筒牛腿初始高差限值分析
以1#、3#、8#筒为例,对角部筒牛腿在竖向位移作用下的反力情况进行分析。
当牛腿发生z正向的竖向位移时,其自身反力会随着位移的增大而增大。以600 kN为牛腿反力限值进行计算:当500 kN级牛腿位移7 mm时,反力超标,以7 mm作为500 kN级牛腿的位移限值。当同一筒内的350、300 kN级牛腿各自位移10 mm以上时,反力超标,因此以10 mm作为角部筒350、300 kN级牛腿的位移限值。
当牛腿发生z负向的竖向位移时,其相邻牛腿反力会随着位移的增大而增大。为方便讨论,以筒内对角线上的2个牛腿同时发生大小相同的负向位移为最不利工况:当300 kN级牛腿发生-8 mm以上的竖向位移时,相邻的500 kN级牛腿反力超标;当250 kN级牛腿发生-6 mm以上竖向位移时,自身与预埋盒脱开;当200 kN级牛腿发生-5 mm以上的竖向位移时,自身与预埋盒脱开。综上,可得角部筒牛腿初始标高控制指标(表3)。

表3 角部筒牛腿初始标高控制指标
此外,初始状态下反力最大的角部筒牛腿受竖向位移的影响效应并非最大。如在3#筒牛腿中,初始反力最大的编号3-3牛腿在位移14 mm时反力超标,而其他牛腿均在位移12 mm时达反力设计极限。
3.2.2 内侧筒牛腿初始标高限值分析
由于内侧筒牛腿反力大部分集中在300~200 kN范围内,因此以300、250、200 kN为初始反力参数将牛腿分为3类,分析在初始标高差异下,这3类牛腿的标高变化限值。
由于内部牛腿反力分布较为均匀,且最大反力相较角部牛腿小,因此当牛腿发生z负向的竖向位移时,其对相邻牛腿反力的影响较相邻牛腿自身位移对其反力的影响要小很多,因此仅就牛腿自身发生标高变化时对自身反力的影响进行分析。
由有限元计算结果可知,当300、250 kN级牛腿的位移达12 mm时,其反力位于580~610 kN区间内,因此将此反力中位数对应的11 mm位移定义为300、250 kN级牛腿的位移限值;当200 kN级牛腿位移达14 mm时,各牛腿反力位于580~620 kN区间,因此将14 mm定义为200 kN级牛腿的位移限值。综上,得到牛腿初始标高控制指标如表4所示。

表4 内部筒牛腿初始标高控制指标
对比表3、表4可知,内筒牛腿位移限值相对角筒牛腿限值要大,因此在实际施工过程中为方便统一操作,可将角筒牛腿的位移限值作为统计控制指标。此外,钢平台角部筒反力最小的牛腿在z负向位移作用下,其与牛腿预埋盒脱开的位移限值要比z正向位移反力达极限的位移限值小很多。综上,在施工过程中需重点关注角部筒中的各牛腿初始标高变化。
3.3 牛腿伸长量限值分析
为方便表达,本节中的牛腿伸长量如图9所示,用以表示牛腿根部悬空部长度。初始状态下内墙未收分时,牛腿伸长量为30 mm。
钢平台在实际施工过程中,内墙总收分量为200 mm,因此需针对牛腿伸长230 mm这一工况进行定性分析。此外,若定性分析满足限值要求,还需讨论内墙收分限值。此工况下取收分量50、100、150、200、250、300、350、400、450、500 mm作为内墙收分工况,针对具有不同初始反力等级的牛腿进行讨论。

图9 牛腿初始伸长量示意
3.3.1 实际使用状态下内墙收分量限值分析
由精细化模型计算得,编号1-2、6-1牛腿初始反力达330 kN,最大Mises应力达160 MPa以上,与发生伸长的其他牛腿相比较为危险。因此取3个牛腿,对其在伸出长度改变作用下的应力变化进行分析,计算结果如表5所示。
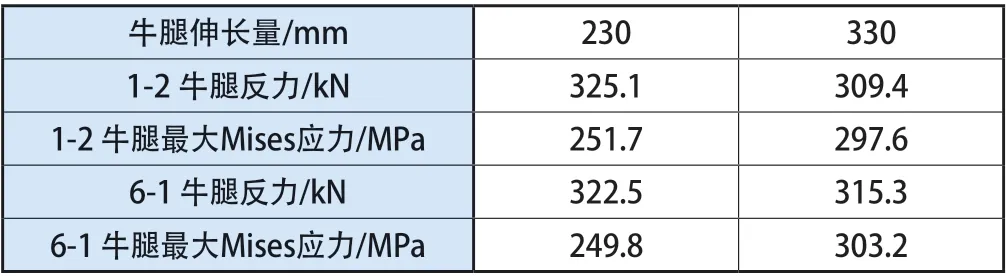
表5 1-2、6-1牛腿反力、应力变化
由表5可知,钢平台牛腿在实际墙体收分工况作用下,当牛腿伸长量达230 mm时,其最大Mises应力达250 MPa,满足Q345钢设计要求。此外,根据其他牛腿计算结果可知,各牛腿应力变化幅度均随伸出长度增大而增大;当牛腿伸长量达330 mm,此钢平台编号6-1牛腿最大Mises应力达极限。因此,可取330 mm作为牛腿伸长量的控制指标。
此外,由编号1-2、3-4、6-1牛腿反力变化趋势线(图10)可得,钢平台牛腿反力与牛腿伸长量的相关系数R接近1,可认为二者线性相关。这表明钢平台牛腿伸长对自身反力的影响要远大于对周边牛腿反力的影响,且各牛腿反力随牛腿伸长而减小,这表明支撑刚度随牛腿伸长而减小。
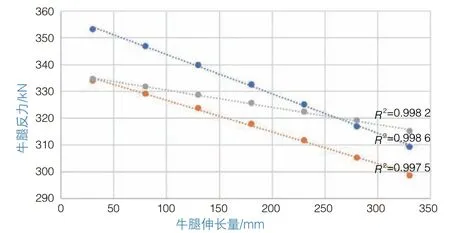
图10 牛腿伸长量-反力变化趋势
3.3.2 不同初始反力等级的钢牛腿伸长限值分析
由于实际工程中核心筒收分方向不一致,故本文以支撑于内墙的钢牛腿为例,取200、250、300 kN为内墙钢牛腿反力参数。
结果表明:300 kN级牛腿伸长量480 mm、250 kN级牛腿在牛腿伸长量达530 mm时,其自身反力达极限;200 kN及以下的牛腿在现有墙体收分极限的条件下,在各施工状态均有足够的安全储备。
4 结语
通过对简化模型及精细化模型中钢平台底部约束系统的计算分析,可得如下结论及建议:
1)8级风作用下,顶墙导轮接触状态的差异可导致筒架柱整体倾斜率、层间位移相较初始状态增大100%、自身分力增大70%,但其仍满足设计限值。当该效应与该极端风载效应叠加作用导致倾斜率超过限值时,可采用层间拉结等方式,确保大部分顶墙导轮与墙面可靠接触。
2)提出搁置状态下钢平台牛腿初始标高分级控制限值。牛腿初始标高变化导致的反力增大与牛腿在钢平台内部的分布位置、初始反力均有关:角部筒500 kN级牛腿,可承受+7 mm标高变化;内部筒300 kN级牛腿,可承受+11 mm标高变化。当牛腿初始标高变化超过规定限值时,可采用增设牛腿垫板等构造措施;当牛腿初始标高变化值为负时,部分牛腿存在脱开的风险,且此风险随牛腿初始反力的减小而增大。初始反力最小的200 kN级牛腿,当标高变化-5 mm时,其与牛腿预埋盒脱开。
3)提出钢平台竖向牛腿伸长量分级控制方法。对于初始反力最大的350 kN级牛腿,可采用330 mm作为牛腿伸长量控制指标;250~300 kN级牛腿,可根据牛腿初始反力,采用480~530 mm作为牛腿伸长量控制指标;当牛腿伸长量超过对应的控制指标时,应采用焊接牛腿加劲板等构造措施减小牛腿应力。
