连通气球实验结果及其定性解释

2014-05-29潘才连蔡志东

镇江高专学报 2014年2期

潘才连，蔡志东

(镇江高等专科学校丹阳师范学院，江苏丹阳 212300)

连通气球是小学生非常喜欢的一个自主探究实验，一些中学生也喜欢这个实验。一些学生和小学科学教师认为，大小不同的2个气球连通后只出现一种结果，即“大的更大，小的更小”。实际上，还存在另外2种现象，即“大的、小的都不变”和“大的变小，小的变大”。原因何在?迄今为止，还没有人对此作出合理的解释。网上有不少人采用肥皂泡模型(即把气球视作肥皂泡)来解释现象——“大的更大，小的更小”，这是错误的。笔者对实验方法作了适当的改进，使得实验操作省时省力，效果显著，并根据橡胶的应力-应变关系曲线对此作出了合理的解释。

1 连通气球实验方法的改进

1.1 传统的实验方法

连通气球取材方便，操作简单，现象奇特，是小学生自主探索实验项目之一，深受小学生的喜欢。文献［1］详细介绍了实验过程。简单地说，就是用2个气球、1根管子、几条棉线，让学生自主探究2个大小不同的气球连通后的变化，培养学生的观察和实验能力。实验装置和步骤如图1所示。

实验过程:1)吹起2个气球，一大一小，分别用棉线扎住(不要打死结);2)把2个气球分别绑在空心管的两端，注意扎紧别漏气;3)打开2个活结，让气球里的空气连通;4)观察气球的变化。

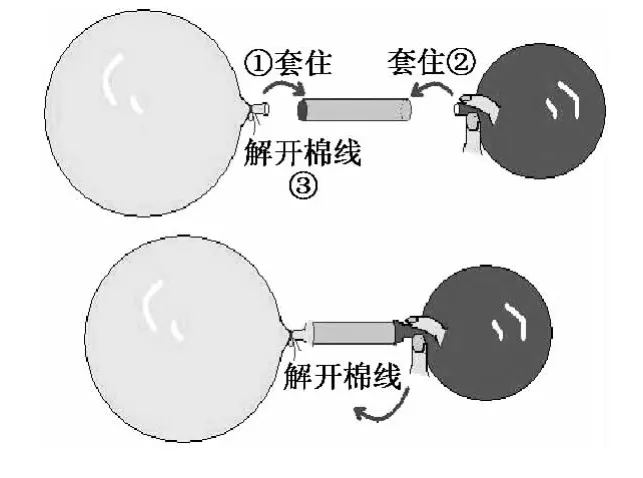
图1 传统的连通气球实验

笔者发现，按照传统的做法，操作起来相当麻烦，而且容易漏气。首先，直接用嘴对着气球吹气不卫生，有些肺活量较小的学生不能一次性把气球吹得很大(一不小心，气球中的气体会反冲回口腔)。其次，直接把气球口套在管子上会因套不紧而漏气，如果用线把它系在管子上，则相当于每个气球上有2个结，共有4个结。多次实验时，需要反复系、解4个结，非常麻烦。再次，不能做到同时打开气球阀门，让气体同时相向而行(左、右2个活结同时打开很难做到)。

1.2 改进后的实验方法

为克服这些不足，笔者做了较大的改进，如图2所示，把原来的1根管子改成3根(较短的)玻璃管，中间用2根较短的乳胶管(乳胶管事先清洗干净)相连，气体的通、断由乳胶管上的2个弹簧夹控制。左、右2根玻璃管的一端和2个气球相连(可以用线扎成死结或活结，非常紧密)，另一端和乳胶管相连，中间玻璃管是活动的，可以很方便地套上或取下(左、右2个)乳胶管。实验时，先把中间玻璃管取下，松开夹子，用嘴或气筒通过乳胶管向气球吹气或打气。若用嘴吹气，一口气吹完后立即用夹子夹住乳胶管，休息片刻，再松开夹子，吹第二口气并夹住。反复多次，可以把气球吹得很大，同时避免气球内的气体反冲。吹到需要的大小之后，把它们和中间的玻璃管相连。然后，2个弹簧夹同时打开，观察气球大小的变化。此法省时省力，效果非常好。

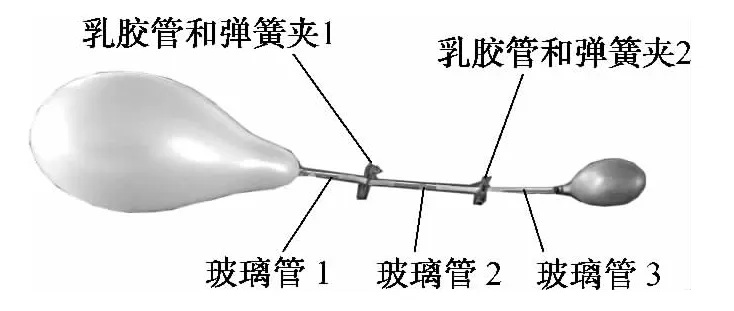
图2 改进后的连通气球实验

2 实验结果

2.1 实验数据、图片及结论

有不少教师和文献认为，实验的结果只有一种:即大、小不同的2个气球连通后大的更大，小的更小。但笔者的实验结果有3种(事实上，一些学生分组实验中也出现过3种现象，只不过被忽视了)。具体结果见表1。

表1 大、小不同的2个气球连通后半径或体积的变化

为了使数据更加可信，笔者用数码相机拍摄了测量过程(注:直尺的起点刻度为10 cm)。以实验1为例(实验2和实验3，略)，图3，图4，图5，图6显示，确实有“大的变小，小的变大”现象存在。

图3 实验1中大气球连通前的直径(21 cm)

图4 实验1中小气球连通前的直径(9 cm)

图5 实验1中2个气球连通后，大气球的直径(19.5 cm)

图6 实验1中2个气球连通后，小气球的直径(13 cm)

2.2 中学生的实验曲线

笔者的实验结论不是孤立的，台湾台南县私立兴国高级中学的许翰棕等4个学生也做了类似的实验［6］，得出了同样的结论，即3种现象都有可能出现。他们还绘出了气球内外压强差(由构成气球的橡胶皮膨胀所引起的张力产生)与半径之间的关系曲线，如图7所示(该设计获台湾第44届中小学科学展览会高中组最佳创意奖)。原图中，纵轴表示压力用T表示。图7中，上面曲线所示为充气曲线，下面曲线所示为放气曲线(从图中可见，与充气曲线形状相似，但压强有所减弱)，压强差ΔP单位是厘米水柱高(cmH2O)，半径R为3个方向半径的平均值(单位为cm)。由图7可知，气球内部的压强(等于压强差与大气压之和)先迅速增大，接着减小，然后增大，这一结果和笔者的实验结论一致。图7中的R1，R2分别为最大压强半径和最小压强半径(可以称之为第一临界半径和第二临界半径)。如果把气球的膜看成是一薄膜(实际上是有一定厚度的)，则可以像液体表面那样引进“等效表面张力系数”，即作用在气球表面单位长度的张力，用γ表示，则

由此可依据ΔP－R关系曲线(图7)画出γ－R关系曲线(图8)。图8中，γ的单位为cm·cmH2O(长度单位cm和压强单位之积)，未用国际单位(国际单位制中，张力系数的单位为N/m)。

图7 气球内外压强差与半径的关系

图8 气球等效表面张力系数与半径的关系曲线

如图9所示，取气球表面的一部分(球冠，其底面圆半径为r，球半径为R)，它对圆心的张角为θ，气球的张力沿球冠的切平面作用在半径为r的圆周上，张力的大小为2πr·γ，它在竖直方向的分力为2πr·γ·sinθ，而气球内部气体和外部大气的压力都垂直于球的表面，由于对称性，沿水平方向一周的合力为零，沿竖直方向的合力方向向上，等效作用在半径为r的平面上，其大小为ΔP·πr2，两者相等，所以

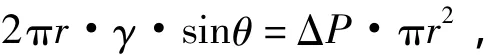
即

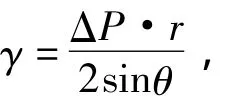
由图9可知，

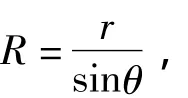
所以

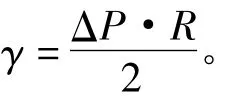
(文献［2］的推导是特例，相当于 θ=90°，r=R的特殊情况。)

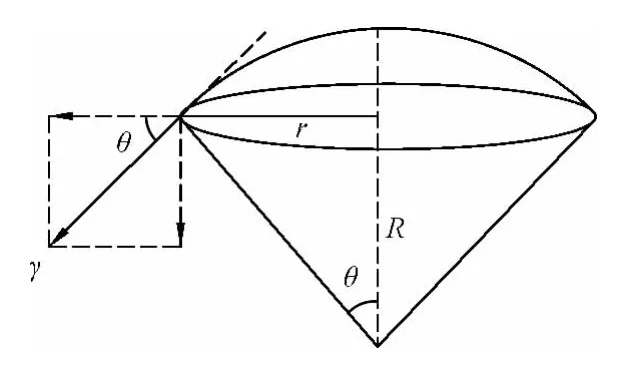
图9 张力系数与半径的关系

3 定性解释

3.1 肥皂泡模型的缺陷

对于连通气球实验中出现“大的更大，小的更小”现象的原因，网上有不少人提出用肥皂泡模型来解释。根据文献［2］和［4］可知，肥皂泡内外压强差的公式为

其中，γ为肥皂水的表面张力系数(在一定温度下为常数)。设P0为大气压强，ΔP=P－P0，公式(1)可改写为

由此可知，半径越大的肥皂泡内部压强越小，当大、小2个肥皂泡连通时会出现“大的更大，小的更小”的现象。但这一模型无法解释2个大小不同的气球连通后会出现“大的变小，小的变大”和“大的、小的都不变”的现象。

事实上，液体的表面张力是由邻近分子的引力引起的［3］，而气球橡胶膜的张力是由弹性体的形变引起的，二者有显著的差异。液体的表面层极薄，气球橡胶膜相对较厚。液体的表面张力系数γ与半径无关(一定温度和杂质下不变)，而气球橡胶膜的张力系数γ是变化的。

3.2 气球薄膜的应力-应变曲线

气球的主要成分为橡胶(此外还有配合剂、稳定剂、硫化剂、防老化剂等非橡胶成分)，是典型的高分子弹性体。根据文献［5］，通用的典型橡胶应力-应变曲线如图10所示(不同弹性体的曲线是有差异的)。

图10 橡胶的应力-应变曲线

所谓“应力”是指单位面积上受到的弹力，其定义为

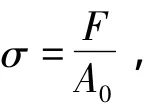
其中，F为载荷或弹力，A0为原始截面积。

所谓“应变”，就是相对形变量，其定义为

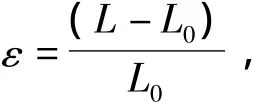
其中，L0为原始长度，L为形变后的长度。应变也叫做应变率，一般用百分比表示。

3.3 应力-应变曲线的主要特征

由图10可知，此曲线大致可以分为3个阶段:

第1阶段，ε约为50%(拉伸后的长度小于原长的1.5倍)，应力随应变的变化很快。在这一阶段，很小的形变就能产生比较大的应力。这一阶段，处于无规卷曲状态的网络链逐渐伸展。

第2阶段，ε约为60% ～260%(拉伸到原长的1.6到3.6倍之间)，曲线上升缓慢，即形变过程中应力增长非常缓慢，这一结论和台湾中学生的实验结论完全吻合。此阶段，除了无规卷曲线团伸展之外，还有一些小的网络链在发生形变。

第3阶段，即ε约为260% ～500%(即拉伸到原长的3.6～6倍)，曲线上升迅速(尤其ε＞400%时，上升极快)。此时，材料内部柔性网络链已充分伸直，较刚硬的结晶和有序微晶区也发生变形而解体，局部有缺陷和裂纹产生并伸展，直至材料的化学键在应力作用下断裂(气球爆裂)。

3.4 用应力-应变曲线解释压强差与半径的关系

由图10可知，在第1阶段，当R增大时，ΔP(本质上就是由弹性体的形变产生的弹力引起的)增大。第2阶段，气球的弹性有所减弱，应力变化极小，但是，气体压力作用的面积却急速增大(与图9中的r2成正比)。于是，ΔP随R的增大而减小。第3阶段，气球膜内部的柔性网络链已充分伸直，应力σ上升很快，总的张力增加得比r2还要快，所以ΔP再次增大，这样就定性地解释了图7。