组合式负荷传感器旋转效应的研究

韦铁平，杨晓翔，姚进辉，许 航

（1.福州大学 机械工程及自动化学院，福建 福州 350002；2.福建省计量科学研究院，福建 福州 350001）

针对目前采用标准砝码检定大型固定式电子衡器存在的工作量大、劳动强度高和运输成本高等的一系列问题，福建省计量科学研究院提出了一种无砝码检定校准系统［1］.组合式负荷传感器是该校准系统的核心部分之一，它的测量准确度直接影响到整个校准系统的测量结果.设计准确度要求为0.02级的负荷传感器，其旋转效应对其测量结果的影响很大，必须严格控制［2］.

在寄生分量的作用下，由于测力仪本身的不对称结构（包括机械与电性能），导致不同方位的示值发生变化的现象，称为旋转效应［3］.旋转效应在力标准机的相互比对测量值中起着非常重要的作用，它对测力仪的不确定度评估影响很大［4］.许多研究人员对此做了大量的研究工作：PTB公司最早对叠加系统进行旋转效应的测量［5］；PETERS［6］分析了测力仪与力标准机的交互作用，指出了弯矩和非轴向力是产生旋转效应的主要原因；BRAY［7］和XU［8］等通过数学模型来解释显示器的输出值与施加试验力之间的关系，并利用正弦函数来表达旋转效应对测力仪测量不确定的贡献；PARK Y K等［9］对叠加系统不同方位进行测量，通过3个力传感器输出信号的差异来获得侧向力分量，并以此来评估叠加系统的复现性.而通过有限元法来分析组合式负荷传感器的旋转效应则鲜有文献报道.

基于国家重大科学仪器设备开发专项“高精度衡器载荷测量仪开发和应用”的研究，姚进辉等［10］提出了带有均力结构的组合式负荷传感器.本文详细阐述了组合式负荷传感器三维有限元网格模型的建立，分析不同寄生分量对力传感器产生的附加侧向力的规律及其与旋转效应的关系.

1 组合式负荷传感器

本文所研究的组合式负荷传感器量程为300 kN，由3个相同的力传感器RTNC3／10T组成.常用的组合式负荷传感器主要由承压板、对中调节压头、力传感器组、力传感器底座和底座组成，其结构如图1a所示.3个相同的力传感器呈120°均匀地排布在底座上.对中调节压头与力传感器的中心轴对应重合.检测系统、传感器结构和操作为理想状况下，3个力传感器输出值应该是相同的.然而现有传感器在检定、校准中经常出现承压板变形，承压板与试验机之间的对中发生偏心、同心倾斜和偏心倾斜载荷等问题，由此造成传感器在不同方位测量时输出示值发生误差，降低了传感器的测量准确度.

图1 两种组合式负荷传感器的结构示意图Fig.1 Schematic diagram of combinatorial load cells

针对以上问题，设计了一种能有效减小旋转效应的均力结构.它由3部分组成：对中调节压头、均力板和推力关节轴承组，其结构如图1b所示.

2 有限元模型的建立

节点受力时，各部件包括推力关节轴承内、外圈及焊接或螺栓固定的两个部件之间都是通过接触传递力.有限元软件ANSYS具有良好的接触模拟分析能力，故选用其进行有限元弹性分析模拟.

2.1 模型简化

为获得在已知的不同寄生分量作用下3个力传感器所受附加侧向力的变化规律，仅将对中调节压头以上的部分作为研究对象.有限元模型共6个部分：承压板，上、下推力关节轴承组，均力板，上、下定位套组，对中调节压头组和施力构件.在边界约束的设置中，部件之间的螺栓连接方式选择绑定接触方式实现，这样既不影响分析结果又保证了网格的规整，同时提高了网格划分的效率.此外，认为承压板以上力的传递机构能保证传递到承压板上的力是均匀的，故设置一个刚性面来替代施力构件.

2.2 单元类型

实体单元采用了solid185单元，该单元是8节点模型，在网格自由划分时可以退化为6节点或4节点模型.接触单元和目标单元（CONTA174，TARGE170）主要用来模拟推力关节轴承内、外圈之间的接触.所采用的轴承为自润滑推力关节轴承，接触面的摩擦系数取0.08.

2.3 单元划分

ANSA是最强的前处理软件之一，它在划分结构复杂的模型方面显示强大的功能.为保证模型网格单元的均匀对称，利用ANSA软件建立1／3模型，然后通过阵列得到完整的模型.划分的原则是单元形状尽量规整，不出现畸形的单元.为了达到这一目的，在单元划分时采用了扫掠划分，这样整个有限元网格比较整齐，单元的畸形率不到1%，从模型上保证了结果的可靠性.无均力结构和有均力结构的组合式负荷传感器模型分别划分35436和72768个单元，其三维有限元网格模型如图2所示.

2.4 材料特性

材料选择40Cr，屈服点是785MPa，抗拉强度为980MPa，弹性模量为2.1×105MPa，泊松比为0.28.

2.5 边界条件及加载方式

为了获得力传感器所受的附加侧向力，对压头底面6个自由度全约束固定.根据牛顿第三定律，力传感器与对中调节压头之间的作用力和反作用力，在同一条直线上，大小相等，方向相反.因此，只需提取对中调节压头的支座反力分量即可获得作用在力传感器上的附加侧向力.

分别对有、无结构的组合式负荷传感器模型进行模拟.试验载荷为满量程力级300kN.载荷工况如下：偏离试验机中心轴1mm，3mm，5mm，7mm和9mm 5个偏心量；与试验机中心轴同心倾斜，角度为0.3°，0.5°，0.7°，1°，1.2°和1.5°6个倾斜量；与试验机中心轴偏心3mm倾斜1°载荷.根据《ISO 376：2004（E ）测力仪校准规范》［11］，选择3个均匀分布的方位进行检测，但这样仅能粗略地评估旋转效应.为了获得更加准确的结果，至少要选取6个方位［12］.本文在每个加载点测试完之后，绕着传感器轴线，依次对60°，120°，180°，240°，300°，360°6个方位进行模拟计算.这样每个加载点都要进行6个方位模拟计算（0°和360°重合），一共对144个模型进行模拟分析计算.

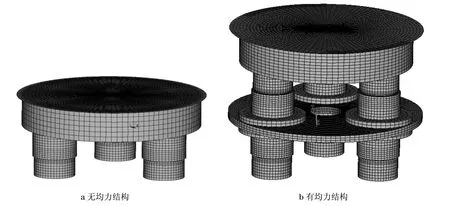
图2 组合式负荷传感器有限元模型Fig.2 Finite－element models of the combinatorial load cells

3 有限元结果分析

3.1 物理量定义

为了深入研究寄生分量与力传感器所受附加侧向力之间的关系，我们引入了以下公式：

在某一寄生分量作用下，组合式负荷传感器中力传感器所受的附加侧向力可表示为：

式中：Fi为第i个力传感器所受附加侧向力；Ai为第i个力传感器所受附加侧向力；θ为第i个力传感器在主坐标上的方位角度；φi为第i个力传感器在主坐标上的初始方位角度，文中均为0.

在某一寄生分量作用下，组合式负荷传感器中3个力传感器所受的平均附加侧向力可表示如下：

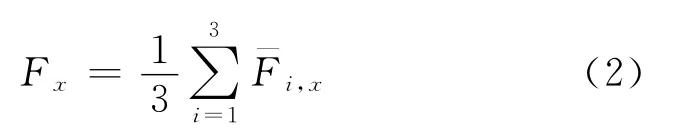
式中：Fx为3个力传感器在寄生分量x下所受附加侧向力的平均值；为第i个力传感器在寄生分量为x、6个方位角度下的平均侧向力.

在某一寄生分量作用下，组合式负荷传感器中3个力传感器所受附加侧向力的波动量可表示如下：

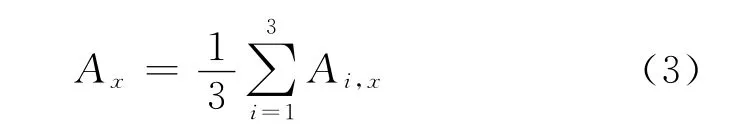
式中：Ax为3个力传感器在寄生分量为x下所受附加侧向力波动量的平均值；Ai，x为第i个力传感器在寄生分量为x下所受的附加侧向力的波动量.

3.2 结果分析

根据以上表达式，我们对模拟结果进行如下分析：

（1）偏心3mm和同心倾斜1°载荷的力传感器侧向力变化规律如图3，4所示.在相同的加载方式下，有、无均力结构3个力传感器的侧向力随着方位角度的变化呈现出正弦波分布.3个力传感器的侧向力波动的振幅相同，初相相差120°.图中曲线显示，均力结构能极大地削弱力传感器的侧向力，并使3个力传感器的附加侧向力趋于平均.

（2）在偏心倾斜载荷作用下，力传感器所受附加侧向力的波动曲线如图5所示.从图5可知，它并非图3和图4的简单叠加.由图4与图5可知，在无均力结构的组合式负荷传感器中，偏心量的加入改变了力传感器侧向力正弦波动曲线的初相；但在带有均力结构的传感器中不受影响.

图3 载荷偏心3mm下力传感器的附加侧向力Fig.3 Additional side loads acting on the force transducers under 3mm－eccentricity load

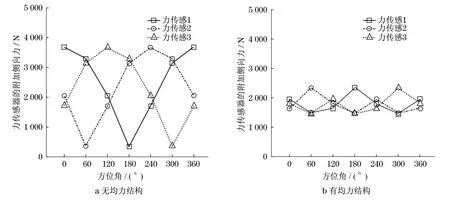
图4 载荷同心倾斜1°下力传感器的附加侧向力Fig.4 A dditional side loads acting on the force transducers under 1°－tilt load

图5 偏心3mm倾斜1°载荷下力传感器的附加侧向力Fig.5 Additional side loads acting on the force transducers under the 3mm－eccentric and 1°－tilt load

（3）力传感器所受附加侧向力平均值如图6所示.从图6可知，无均力结构的力传感器侧向力的平均值始终大于带有均力结构的.偏心载荷作用下，有均力结构的平均值基本不发生改变，而无均力结构的平均值也仅有略微增加.同心倾斜载荷作用下，平均值都随着倾斜角度的增加而增加.有均力结构的平均值增加速率保持稳定，而无均力结构的平均值增加速率逐渐增大，在倾斜1.2°以后与有均力结构保持相同的增加速率.

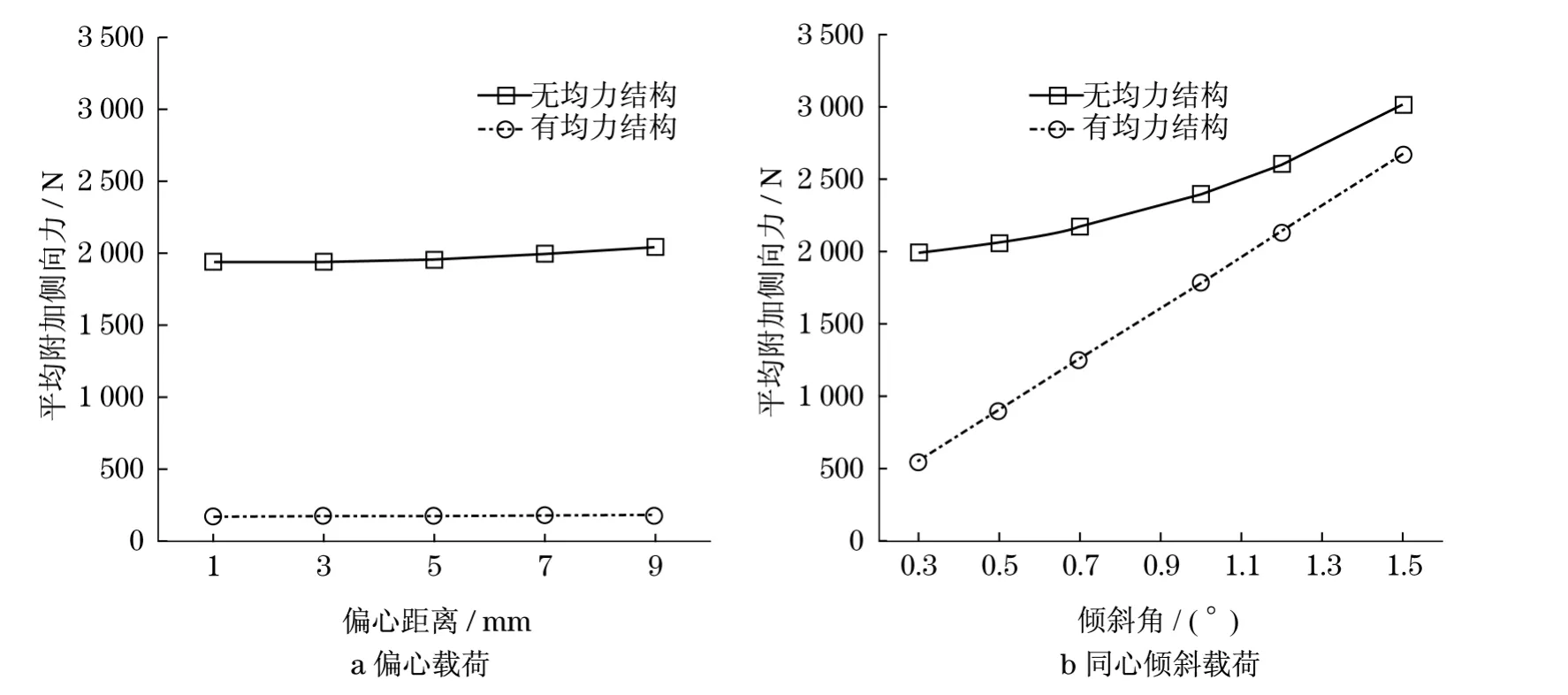
图6 力传感器的平均附加侧向力Fig.6 Average of additional side loads acting on the force transducers

（4）有、无均力结构的传感器在不同寄生分量下力传感器附加侧向力的波动量变化规律曲线如图7所示.从图7可知，均力结构能有效地削弱力传感器侧向力的波动量；倾斜载荷比偏心载荷产生的力传感器侧向力波动量大，倾斜载荷是造成力传感器侧向力波动量大的主要因素.

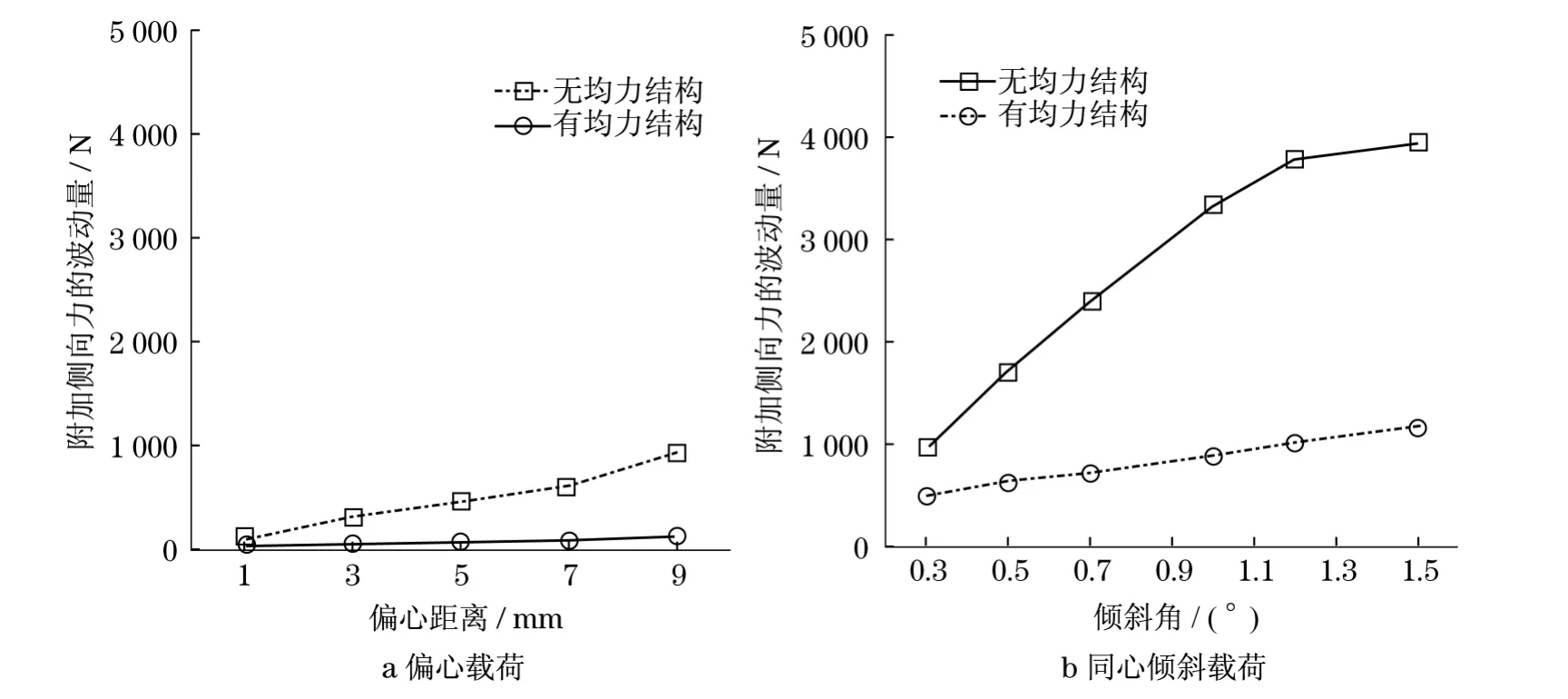
图7 力传感器附加侧向力的波动量Fig.7 Amplitude of the additional side loads acting on the force transducers

4 试验验证

文献［12］针对两种组合式负荷传感器结构在偏心3mm倾斜1°的试验力作用下进行了试验，数据处理结果如图8所示.从图8可知，试验力在每个力级上的旋转效应都有大幅度的减小，可达1个数量级.图5中力传感器所受的附加侧向力曲线变化趋势与实验获得的旋转效应变化趋势相吻合，从而表明以上模型的可靠性.在同一力级下，力传感器所受的附加侧向力波动量越大，组合式负荷传感器的旋转效应也越大.因此，力传感器上的附加侧向力可以作为组合式负荷传感器进行结构优化的一个评定依据.

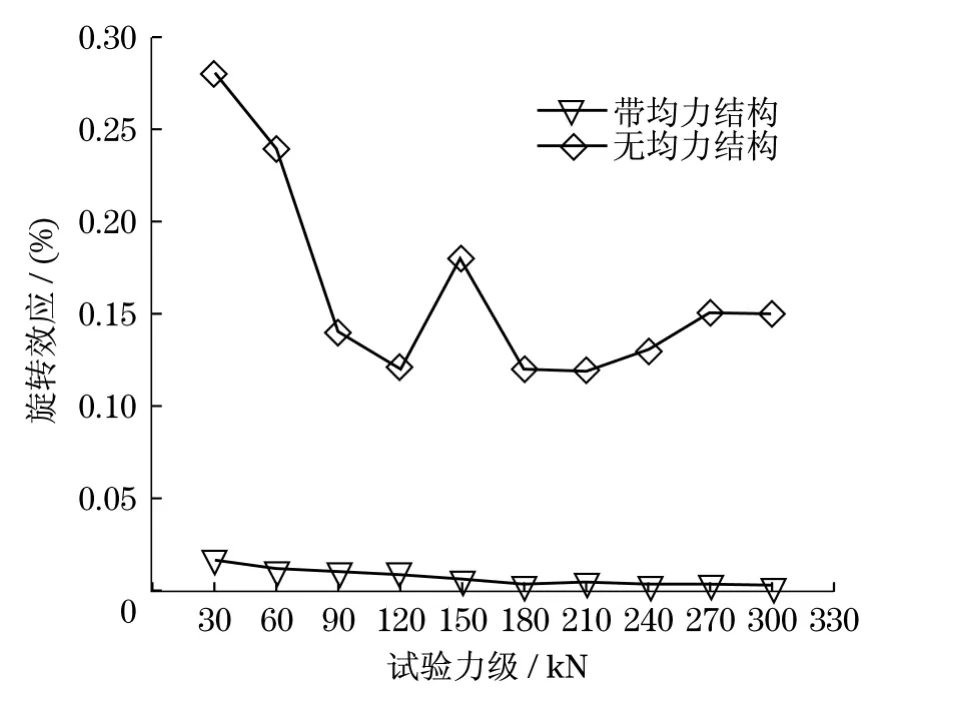
图8 两种组合式负荷传感器的旋转效应Fig.8 Rotation effect of combinatorial load cells

综上分析，均力结构对力传感器的平均侧向力及其波动量都有了很大的削弱作用，由此降低了组合式负荷传感器的旋转效应.力传感器所受附加侧向力的波动量可作为预测同一力级下组合式负荷传感器旋转效应的大小.对于偏心加载，力传感器的平均侧向力较小且波动量不大，则旋转效应也小；对于同心倾斜和偏心倾斜加载，力传感器的平均侧向力较大且波动量也很大，则旋转效应也大.此外，倾斜试验力是造成力传感器侧向力波动的主要因素.

5 结论与展望

通过对两种组合式负荷传感器模型在偏心载荷、同心倾斜载荷和偏心倾斜载荷作用下的有限元模拟分析，获得不同寄生分量下均力结构对力传感器附加侧向力的影响规律.均力结构能有效地减小力传感器侧向力的平均值及波动量，从而有效降低组合式负荷传感器的旋转效应.力传感器所受侧向力的波动量可用于预测同一试验力级下组合式负荷传感器旋转效应的大小，为组合式负荷传感器的结构优化提供了一种依据.倾斜试验力是造成力传感器侧向力波动的主要因素.同时，实验数据验证了有限元模型的可靠性.下一步将利用本文有限元模型探讨均力板的结构及材料特性对均力效果的影响规律.

［1］姚进辉.采用非砝码检定大型固定式电子衡器的研究［J］.中国计量，2011，48（5）：88－90.YAO Jinhui.Study of calibrating the large stationary electronic weighing apparatus without weight［J］.China Metrology，2011，48 （5）：88－90.

［2］国家质量监督检验检疫总局.JJG 144—2007标准测力仪检定规程［S］.北京：中国计量出版社，2007.State Administration for Quality Supervision and Inspection and Quarantine.JJG144—2007Test procedures for the standard dynamometer ［S］.Beijing：China Metrology Press，2007.

［3］国家质量监督检验检疫总局.JJF 1011—2006力值与硬度计量术语及定义［S］.北京：中国计量出版社，2007.State Administration for Quality Supervision and Inspection and Quarantine.JJF 1011—2006Measurement terms and definitions for the force value and hardness［S］.Beijing：China Metrology Press，2007.

［4］PETERS M.Experiences and results of international comparison measurements of forces up to 1MN［J］.PTBMitteilungen，1989，99（5）：343－350.

［5］WIERINGA H.Design of a 1.65MN and 4.95MN transfer standard based on the build－up procedure［C］∥Proc.of 10th IMEKO TC－3Conference，Berlin：Springer Press，1984：67－77.

［6］PETERS M.Limits to the uncertainty achievable in force transfer［J］.Measurement，1984，2（4）：197－202.

［7］BRAY A，BARBATO G，FRANCESCHINI F，et al.Rotational and end effects：a model for uncertainty evaluation in force measurements by means of dynamometers［J］.Measurement，1996，17（4）：279－286.

［8］XU C.A practical model for uncertainty evaluation in force measurements［J］.Measurement Science and Technology，1999，9（11）：1831.

［9］PARK Y K，KIM M S，KIM J H，et al.A proposal for an evaluation method of force standard machines by using buildup system［C］∥Proc.of the IMEKO TC－3Conf.on Measurement of Force and Mass，Berlin：Springer press，2005.

［10］福建省计量科学研究院.一种测力传感器结构［P］.中国：201110449912.3.2011.Fujian Province Institute of Metrology.A structure of force transducer［P］.China：201110449912.3.2011.

［11］International Organization for Standardization.ISO 376－2011 Metallic materials—Calibration of force proving instruments used for the verification of uniaxial testing machines［S］.Geneva：International Organization for Standardization，2011.

［12］姚进辉.组合式负荷传感器方位误差的减小［J］.中国计量，2013，38（3）：74－76.YAO Jinhui.Study of calibrating the large stationary electronic weighing apparatus without weight［J］.China Metrology，2013，38（3）：74－76.