基于CPSO－BP神经网络的柴油机排气门间隙故障诊断

李 岩，袁惠群，，梁明轩，赵天宇

（1.东北大学 机械工程与自动化学院，沈阳 110819；2.东北大学 理学院，沈阳 110819）

发动机在冷态下，当气门处于关闭状态时，气门与传动件之间的间隙称为气门间隙.气门间隙异常是柴油机的典型故障［1］.间隙过大，降低了气门的开启高度，使发动机功率下降，配气机构零件撞击增加，磨损加快；间隙过小：使气门关闭不严，造成漏气、功率下降，甚至导致密封表面积碳烧坏.传统的人工检测方法要比对出厂压力标准，操作复杂，难以实时检测.与传统处理方式相比智能诊断技术逐渐成为故障诊断中的关键技术，如神经网络和支持向量机等.文献［2－3］以支持向量机作为故障分类器，实现了对气门间隙异常的故障诊断.文献［4］采用LabVIEW构建了基于经验模式分解与准BP神经元网络进行故障聚类的内燃机排气门间隙故障诊断系统，并对该系统的准确性进行了试验验证.文献［5］借助遗传算法引入了基于统计规则的智能数据挖掘技术，通过大量对不同气门状态下气门缸盖振动信号的分析，对气门故障进行了有效诊断.粒子群优化算法（Particle Swarm Optimization，PSO）是一种基于迭代的优化工具，具有全局寻优的特点，而且它在优化神经网络时，无需导数等梯度信息，具有实现简单且全局优化性能好的特点，可很好地解决神经网络的结构和权值优化等问题.然而PSO解决多分类问题困难，且其初始参数选取困难，极易陷入局部最优，为此引入混沌变量（Chaos）.

本文在标准PSO算法的基础上结合混沌搜索的方法改进了其寻优效率，对BP神经网络权值、阈值以及网络结构进行优化，将得到的CPSO－BP神经网络聚类模型用于柴油机故障诊断中.通过算例分析和试验对比，结果表明该模型能有效地用于柴油机气门间隙故障诊断，且具有很好的鲁棒性.

1 CPSO算法

由于PSO算法在全局最优解附近的搜索效率有明显降低，容易陷入局部最优解，不能满足优化需要，在此引入混沌搜索.因混沌变量的遍历性和变化随机性可以将其引入优化搜索用以改良优化算法，使算法容易跳出局部最优解，改善全局搜索能力［9］.在此将PSO算法与混沌搜索相结合，得到混沌粒子群算法，其原理如下：

因其遍历性及随机性，混沌策略常被用优化，并已多次被融合进粒子群算法，帮助粒子逃离局部最优.现尝试当粒子群进化收敛，即全局最优值的变化小于某个给定的值ε时，将种群按给定概率Pm进行混沌映射.具体方法为对所有非全局最优粒子配置分布于［0，1］之间的随机数r，如果r小于Pm，则在该粒子中随机抽取一维变量进行Logistic混沌映射.

（1）对于决策变量，其中i表示n维变量x中第i个位置元素，k表示迭代次数.首先令k＝0，其映射为0到1之间的混沌变量其中xmin，i和xmax，i分别为第i维变量的搜索上下界.

（3）将混沌变量转换为决策变量，

（4）根据决策变量对新解进行评价，若新解优于初始解或者混沌搜索已经达到最大迭代步数，将新解作为搜索结果.

2 基于CPSO－BP神经网的排气门间隙故障诊断

2.1 试验与数据采集

本文试验对象为康明斯6BT5.9型柴油机，测试与数据处理系统的原理如图所示.将第4缸排气门间隙依次设置为0.2mm（过小）、0.4mm（正常）、0.6mm（过大），其他缸间隙设置为正常.据此定义3种故障状态：气门间隙过小、气门间隙正常、气门间隙过大.所有试验均在1 200r·min－1无负荷时进行.在第4缸缸盖排气门左侧粘贴加速度传感器，在喷油泵齿轮轴上安装压缩上止点脉冲传感器用以来标定1缸压缩上止点.信号测量为等时采样，采样频率20kHz.

图1 试验系统原理Fig.1 Experiment system principles

2.2 故障特征提取

EMD方法通过不断剔除信号上下包络曲线的均值曲线将非平稳信号平稳化［10－11］.分解中止条件函数选用其中，emax，emin分别为上下包络线，a（t）为经验模式分解的中止条件函数.

在时域测量过程中，采用一定的时域窗口进行采样，通常采用阿伦方差来表征时域的频率稳定度。阿伦方差的定义式为:

经EMD分解后的各单分量固有模态函数（Intrinsic Mode Functions，IMF）分别代表了一组特征尺度下的平稳信号，而各频带能量的变化可以表征排气门间隙异常情况下的故障特征.由于排气门落座产生的振动响应，其能量主要集中在高频区域，因此拟从前几个分量中提取故障特征信息（本文选取前6个IMF分量）.特征提取过程如下：

（1）对原始振动信号进行EMD分解，选取包含主要故障信息的前n个IMF分量；

（2）求各IMF分量的总能量Ei

式中：其中ci（t）为第i个本征模分量.

（3）构造特征向量T元素为能量

对T向量做归一化处理

式中：E为归一化后的能量.

定义能量百分比Ri为

得到归一化后的特征向量T′作为输入特征向量.

每种工况下随机进行多次测试，取30组数据作为训练样本，表1为从12个实测样本中提取的特征参数，其中1—4为排气门间隙0.2mm时的数据；5—8为排气门间隙0.4mm时的数据；9—12为排气门间隙0.6mm时的数据，作为测试样本.

表1 各样本的特征参数Tab.1 Characteristic parameters of the samples

2.3 神经网的权值优化与结构优化

2.3.1 神经网的权值优化

粒子群算法对神经网络权值优化的思路为：首先针对特定的神经网络列出所有神经元，并将所有神经元可能存在的连接权值编码成一个向量；随机生成的这些向量作为粒子的参数初始化粒子；计算所有训练样本通过此神经网络的均方误差作为每个粒子的适应度；待达到最大循环次数或者适应度值满足需求后的全局最优解即可作为神经网络的权值和阈值得到训练后的神经网.步骤如下：

（1）根据神经网络的结构将神经元间的连接权值和阈值顺序编码成一个向量并归一化到［－1，1］空间.

（2）混沌初始化粒子群，初始化粒子的初始位置、速度、惯性权重ω及加速因子c1，c2.最大迭代次数：随机产生元素在0～1之间的C列1维向量，C为目标函数中变量个数，计算粒子适应度值.

（3）将粒子群中每个分量（粒子）映射为网络中的权值、阈值，构成神经网络.对每个个体对应的神经网络，输入训练样本进行训练，计算每个网络在训练集上产生的均方误差作为适应度函数F：

式中：tk，p为理想输出值；Y为在权值阈值构建为向量X时的实际输出值；n为训练样本个数；c为输出节点个数.

保存每个粒子的自身最佳位置，更新全局最优最佳位置，开始迭代.

（4）更新粒子的速度和位置，并用Tent映射与Logistic映射产生的混沌点阵，选择能量最低点作为粒子更新位置.

（5）检验是否符合结束条件.如果适应度函数值小于设定的结束条件变量ε→0或者达到最大迭代次数时算法终止，保存全局最佳位置.否则转入步骤（3）继续迭代.

（6）将全局最优解还原为神经网的权值和阈值得到训练完毕的神经网.

2.3.2 神经网的结构优化

对于一般模式识别问题，3层网络可以很好地解决问题，因此，仅设计1个隐含层即可.根据Kolmogorov定理［13］公式，最佳隐含层节点数可参，其中，l为输出层节点数，m为输入节点数，n为输出节点数，a为0～10之间的随机数.以表1数据R1—R6构成6维输入向量，以表2所示3种状态构成3维网络输出向量.即输入层有6个节点（n＝6），输出层有3个节点（l＝3）.计算得的取值范围为1～13，问题转化为l在此范围内最优值.优化算法依然采用2.3算法，个别细节略有不同，简略步骤可叙述为：取隐含层节点的上限值13建立神经元网络，粒子的编码采用二进制编码，每个粒子为0－1编码的13位二进制数值，1代表此节点有效，反之无效.速度更新用粒子的交叉和变异代替.交叉定义为通过与个体极值和群体极值交叉来更新个体.变异则采用个体内部两随机位互换的方法，首先随机选择变异位置1（position1）和变异位置2（position2），然后把两个变异位置的节点有效性互换.适应度函数采用式（6）同权值优化.经计算得到最优值为12.

2.4 故障聚类

基于神经网络的诊断方法就是利用神经网络对柴油机故障进行模式分类.神经网络直接用于故障诊断时，要挑选特征参数（本文用分解后的IMF的能量百分比）组成输入向量，以故障原因作为输出向量，利用典型样本学习所得权值进行模式识别.由2.1描述的3种故障类型构建输出向量为3的元素向量，如表2所示.

表2 故障类型编码Tab.2 Code of fault type

取2.3.2优化后的神经网结构，输入层传递函数选用Tansig（），输出层传递函数使用purelin（）.在混沌PSO优化神经网的过程中，取ω＝0.729 84，c1＝c2＝1.496 172，50个粒子，粒子的取值上下界xmin＝－5，xmax＝5，对此神经网进行权值优化.

标准BP网、优化后的神经网分别用训练数据训练，用测试数据测试得到聚类结果如表3所示.

表3 诊断结果对比Tab.3 Diagnostic results contrast

2.5 优化方法比较分析

为了分析比较不同优化方法的误差，分别绘制了神经网、标准粒子群算法以及单独使用BP神经网优化的误差曲线.表4为均方误差最小值以及最后识别正确率统计.

图2为使用BP神经网自带训练函数训练神经网迭代次数与权值阈值均方误差曲线图，训练次数为100次.可见其均方误差最小值为0.036，其值并不线性收敛.利用此神经网进行故障聚类最后的识别正确率为95.83%.

表43 种方法诊断结果对比Tab.4 Comparison of three methods diagnostic results

图2 标准BP网均方误差曲线Fig.2 Standard BP neural network MSE curve

图3为使用标准粒子群算法训练神经网迭代次数与权值阈值均方误差曲线图，其均方误差为0.003 4，最优解收敛于48次循环之后.利用此神经网进行故障聚类最后的识别正确率为100%.

图4为使用本文算法训练神经网迭代次数与权值阈值均方误差曲线图，其均方误差为0.000 6，仅6次循环就找到最优解.利用此神经网进行故障聚类最后的识别正确率为100%.

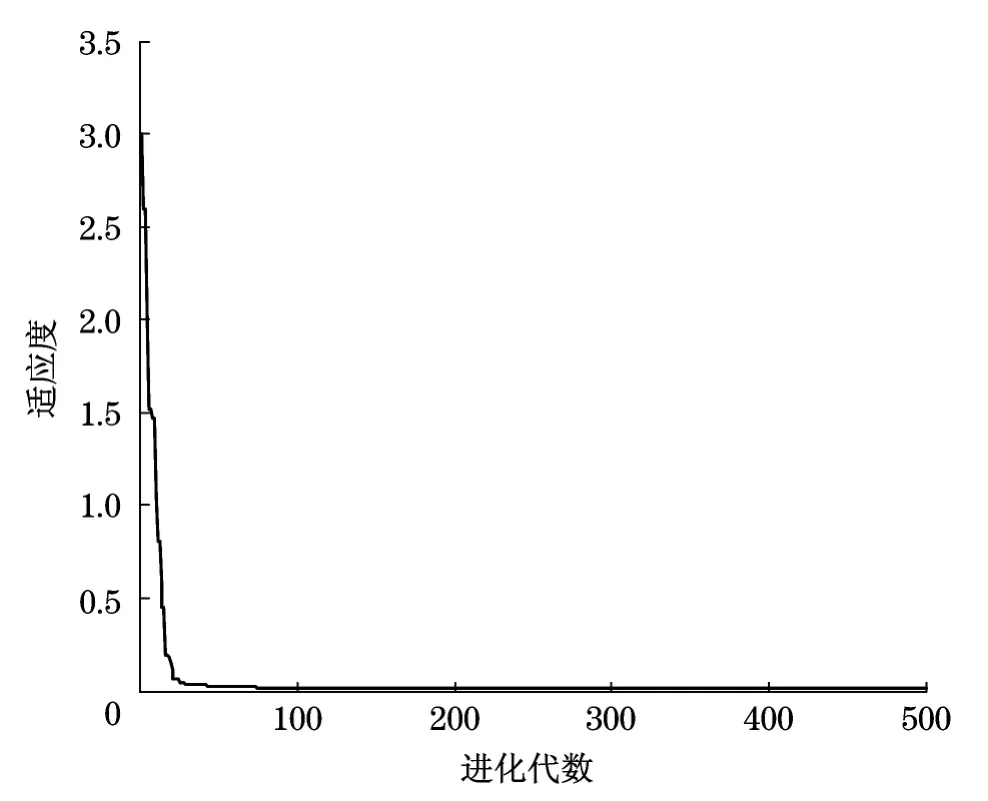
图3 PSO优化神经网均方误差曲线Fig.3 PSO algorithm optimized neural network MSE curve

由表4可见混沌PSO算法优化后的神经网的识别正确率和误差以及求解速度对于其他两种方法均有较大优势，对于柴油机故障实时聚类问题具有较高的有效性和可靠性.

图4 混沌PSO优化神经网均方误差曲线Fig.4 Chaos PSO algorithm optimized neural network MSE curve

3 结语

用混沌PSO算法训练BP神经网络，训练结果在收敛速度和降低误差上均有显著提高，可做到实时诊断.通过柴油机故障诊断的应用，对通过经验模式分解方法处理的数据采用MATLAB设计了神经网并用混沌PSO算法进行优化.说明此类神经网对故障的分类具有很高的准确性、可靠性，适用于多种故障诊断场合，具有良好的推广价值.此外本文中神经网隐含层的设计使用的是试凑法，混沌粒子群算法在神经网络的结构设计方面一直表现优异，可作为进一步研究内容.

［1］王涛，李艾华.采用多层核学习机的柴油机气门机构故障诊断［J］.振动、测试与诊断，2010，30（4）：462－464.WANG Tao，LI Aihua.Use multilayer nuclear machine learning mechanism of fault diagnosis for diesel engine valve［J］.Journal of Vibration，Measurment ＆ Diagnosis，2010，30（4）：462－464.

［2］曹龙汉，武明亮，何俊强，等.基于DE－SVM的柴油机气门故障诊断方法及应用［J］.仪器仪表学报，2011，32（2）：323－328.CAO Longhan，WU Mingliang，HE Junqiang，et al.Diesel engine valve fault diagnosis method based on DE－SVM and its application［J］.Chinese Journal of Scientific Instrument，2011，32（2）：323－328.

［3］王祝平，王为.基于EMD与神经网络的内燃机气门间隙故障诊断［J］.农业机械学报，2007，38（12）：133－136.WANG Zhuping，WANG Wei.Fault diagnosis of engine valve based on EMD and artificial neural network［J］.Transactions of the Chinese Society for Agricultural Machinery，2007，38（12）：133－136.

［4］杨文献.基于数据挖掘的柴油机气门故障诊断技术研究［J］.机械工程学报，2004，40（10）：25－29.YANG Wenxian.Date mining based technique for diagnosing the faults presenting on engine valves［J］.Chinese Journal of Mechanical Engineering，2004，40（10）：25－29.

［5］KENNEDY J，EBERHART R C.Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks，Piscataway：IEEE Service Center，1995：1942－1948.

［6］SHI Y，EBERHART R.A modified partical swarm optimizer［C］∥ Proceedings of IEEE International Conference of Evolutionary Computation，Piseataway：IEEE Press，1998：69－73.

［7］KENNEDY J，EBERHART R C.Swarm intelligence morgan［M］.San Francisco：Kaufinann Publishers：2001.

［8］姚俊峰，杨献勇，基于混沌变量的变步长梯度下降优化算法［J］.清华大学学报：自然科学版，2003，43（12）：1676－1678.YAO Junfang，YANG Xianyong.Decreasing gradient optimization algorithm with variable step length based on chaotic variables［J］.Journal of Tsinghua University：Science and Technology，2003，43 （12）：1676－1678.

［9］HUANG N E，SHEN Z，LONG S R，et al.The Empirical mode decomposition and the Hilbert spectrumfor nonlinear and nonstationary time series analysis［C］∥Proceedings of the Royal Society of London Series，London：Carlton House Terrace，1998：903－995.

［10］HUANG N E，SHEN Z，LONG S R.A new view of nonlinear water waves：the Hilbert spectrum［J］.Annual Review of Fluid Mechanics，1999，31：417－457.