无疑处生疑 有疑处释疑——国优课“二次函数的概念”教学片断赏析与思考

唐 芬，朱德全



无疑处生疑 有疑处释疑——国优课“二次函数的概念”教学片断赏析与思考

唐 芬1，朱德全2

（1．重庆市永川中学，重庆 永川 402160；2．西南大学 教育学部，重庆 400715）

学生数学学习的过程是“无疑—有疑—无疑”的循环和超越过程．有疑和无疑是一对矛盾．教师的作用是“教”有疑与“教”无疑：无疑者需“教”而有疑，即无疑处生疑；有疑者又应“教”而无疑，即有疑处释疑．这便是“教”有疑与“教”无疑的辨证处理要诀，也是“教”有疑和“教”无疑的理想境界．

有疑；无疑；问题；概念教学；二次函数

问题是数学的心脏．因此，为问题而教，是数学教学的出发点和着眼点．数学是由问题构成的，教学目标需要问题来展现，教学过程需要问题来活化，教学对象需要问题来触动．离开问题，数学教学仅定位于单向的静态的传输系统．可见，问题应是数学教学的逻辑起点，问题和问题解决是数学教学的生长点[1]．古人说：“学起于思，思源于疑．”有疑才有问，有问才有思，有思才有得．疑问是思维的火种，思维以疑问为起点．南宋理学家朱熹说：“读书无疑者，须教有疑；有疑者，却要无疑，到这里方是长进．”[2]这说明“有疑”和“无疑”是一对矛盾：无疑者，需“教”而有疑，即无疑处生疑；有疑者，又应“教”而无疑，即有疑处释疑．

目前，数学课程改革己进入“后课改时代”，但数学教学中仍普遍存在“缺乏问题意识，重结果轻过程，掐头去尾取中段，在数学对象的背景、引入、形成上着墨不够，导致数学对象的学习过程被浓缩”等“去问题化”现象[3]，这不利于学生创新精神的培养和数学素养的提高．数学课堂如何为“疑”而教，回归数学本质，做到“教有疑”与“教无疑”呢? 这不论是过去还是当下，也是未来数学课堂的永恒主题．这里以“国优课”（第八届全国初中青年数学教师优质课评比一等奖课例）参赛选手王文俊老师的“二次函数的概念”为例，对“教有疑”与“教无疑”做些诠释．研究者认为，整堂课以问题为驱动，理性自然，把“疑”贯穿教学全过程，让学生体验数学地建构概念、形成概念、应用概念、延伸概念，逐步学会数学地认识和解决问题．

1 概念链接 学似无疑

1.1 教学片断呈现

师：八年级我们学习过函数概念，你能说说什么是函数吗？

先后有3名学生回答并相互补充后得出较完整的函数概念，教师屏幕显示．

追问1：你认为函数概念中有哪些关键词？

追问3：我们已经学过了哪些函数？……

追问4：以一次函数为例，说说主要研究了函数的哪些内容？……

师总结：我们学习一次函数经历了这样的过程（顺序播放图1）：从实际问题中，找到两个变量，如果它们存在一定的依赖关系，就得到一个函数，画出函数图象后，通过直观观察，总结出函数的性质，最终又回到实际问题．所以数学来源于生活，也必将应用于生活．今天我们还要学习一种新的函数，请看实际问题．

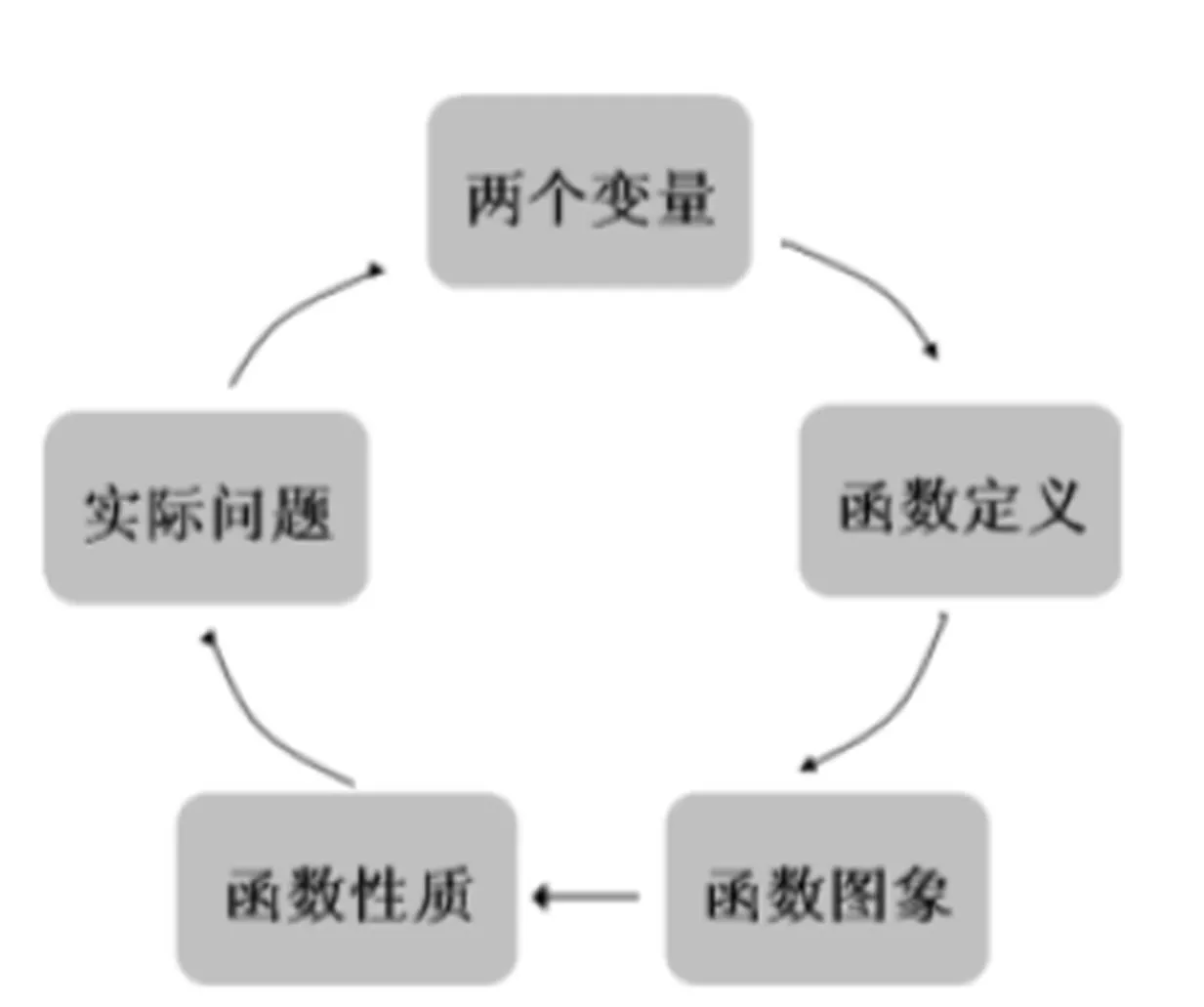
图1

情境二：用16米长的篱笆围成长方形的生物园饲养小兔：

（本片段主要采用问答式，问题解决顺利，其中情境五有适当点拨，教师板书6个解析式．）

1.2 评析与思考

李邦河院士认为“数学根本上是玩概念的，不是玩技巧．技巧不足道也！”苏联教育家克鲁普斯卡娅曾说：“数学是许多概念组成的锁链．”由此可见，数学是思维的体操，数学概念是数学思维的细胞，问题是数学概念的活性酵母[4]，它源自教学目标，成于情境的潜在预设．通过复习，聚焦函数概念中始终不变的属性——“对应”[5]，帮助学生厘清了变量、函数、常量等概念系统，再现一次函数的学习过程；然后基于学生的生活现实，着眼于学生的最近发展区，逐级而上地提出5个情境问题，为学生创设直觉思维场情境[6]，学生顺利完成，没有疑点和错点．尽管学生看似无疑，但教者实属有意：前面的复习既是本章的导学，也为“通过类比探究二次函数”提供了认知基础；后面5个情境问题是执教者对教材的整合，教材的情境问题只有二次函数模型，执教者增加了一次函数、反比例函数、无理函数模型，然后引导学生从众多的模型中抽象出二次函数的特征．如何抽象？其特征是什么？问题亦蕴藏于预设的逻辑情境中．

2 概念建构 贵在生疑

2.1 教学片断呈现

师：同学们，请观察刚才列出的6个关系式，它们都是函数吗？

生齐答：是．

师：哪些是我们已经学过的函数呢？

生1：第（2）个是一次函数，第（4）个是反比例函数．

师：那我们来看看余下的4个函数，它们有什么特点？

学生思考、交流、讨论．

生3：我不同意，（5）与其它3个函数不一样，右边的式子不是二次整式，而是二次根式．

生4：它们都是二次整式．

师：非常好！你能类比一次函数的概念，尝试给二次函数下定义吗？

2.2 评析与思考

数学的严谨呈现为“冰冷的美丽”，但是数学的发现却是“火热的思考”[8]．二次函数概念不是凭空产生的，是源于函数知识本身发展的需要和必然，是基于情境问题解决之需要，这是概念形成的逻辑起点．通过问题驱动，蕴含于问题情境的新旧概念矛盾已经凸显，引发了学生原有的认知冲突，从而诱使新概念的推出，为学生搭建了主动建构的问题支架，学生的思维自然而然地卷人其中，探求新函数的愿望油然而生，二次函数概念的形成亦水到渠成．

3 概念辨析 妙在释疑

3.1 教学片断呈现

本片段采用问答式，课堂气氛活跃，学生发言踊跃，当学生做出判断后，教师及时追问判断理由．完成本例后，师生继续对话．

师：通过这8个函数的辨析，你认为判断二次函数的标准是什么？

生1：满足两个条件，首先，代数式部分应该整式；其次，自变量最高次是二次．

师：这8个函数中，（1）和（5）确定是二次函数，定义域是一切实数．把它放在实际问题中，如情境一、二中的二次函数，自变量的取值还是一切实数吗？

师：为什么呢？

师：遇到实际问题时，自变量的取值范围还要考虑实际问题是否有意义……

3.2 评析与思考

对于二次函数概念的理解，除了清楚概念的内涵，还必须明晰概念的外延．为此，教师根据学生的易错、易漏、易混点，精选了8个函数，设置了两个有价值的问题：为什么是二次函数？又为什么不是？以二次函数的正例和反例为载体，把新的基本概念从正反两方面讲[9]，在每一步“是”或“非”的问题上，小心质疑，让学生“卷入”对概念的辨析、质疑、释疑之中，达到豁然开朗的境地，逐步掌握判断二次函数的标准，形成用概念作判断的“基本规范”，推动学生对二次函数概念的内涵和外延的理解；然后进一步设问，丰富学生对自变量取值范围的认知，为后续学习二次函数的相关知识提供有效保证．正如哲学家陆九渊所说：“学者有疑，小疑则小进，大疑则大进．疑者，觉悟之机也．一番觉悟，一番长进．”[2]

4 概念应用 却要无疑

4.1 教学片断呈现

例2 如图2，在边长为10的正方形中，是边上一动点，以为边长在形内作正方形，点在边上，连接、．当在边上运动时，探究图中变量之间的函数关系．

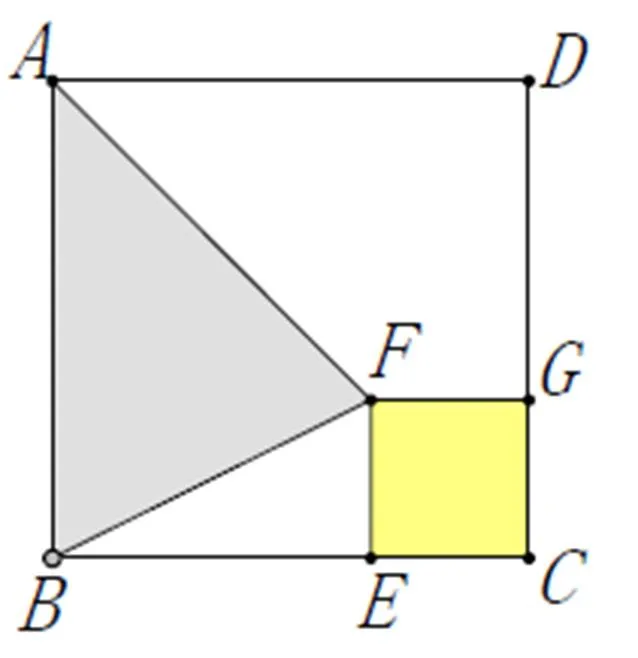
图2

图3

师：（启动几何画板，反复拖动点）请同学们观察图2，在点的运动过程中，图形中哪些量发生变化？

生1：线段的长度，如线段、、、等．

师：还有其它量发生变化吗？

生2：周长．

师：哪些周长？……还有吗？

生2：△、△，还有正方形，它们的周长都在变．

生3：还有梯形的周长也在变，它们的面积也在随着变化呢．

生4：角的大小也有发生变化……

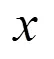
全班练习，学生先后主动板演．

师：生8，你能解释一下为什么吗？

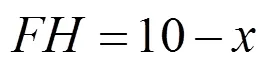
师：这些变化的量与x是一次函数关系，还有二次函数关系的吗？

全班练习，适时交流讨论，学生思维活跃，有答案后主动板演并讲解理由．

生11：梯形的面积：

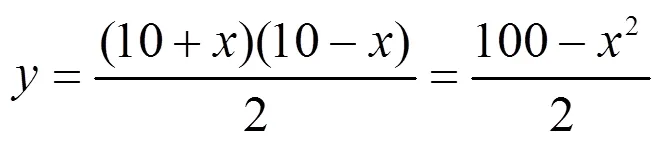
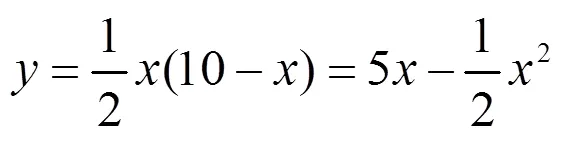
师：这些都是一次函数和二次函数，有没有其它的函数关系呢？

……

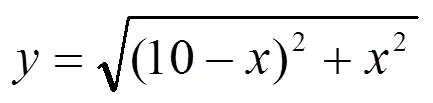
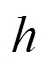
（1）分别求刚开始抛物与抛出4秒时，物体离地面的高度；

（2）抛出的物体经过几秒钟落到地面上？

教师活动：请生念题．电脑模拟上抛运动．（1）中刚开始抛物是什么时候？

师：（2）中什么叫落到地面上？

师总结：数学是学习物理和化学的工具……

4.2 评析与思考

例2的设置，充分展现了执教者的创新精神和数学素养，也是本课的最大创新和特色所在．该例问题开放，先任意找两个变量，再建立函数关系，其结果可能是一次函数、二次函数，或其它函数．借助几何画板的动画功能，启动学生的几何直觉思维，教师适时提出系列问题：“在点的运动过程中，图形中哪些量发生变化?”“哪些变量与是一次函数关系?”“……还有二次函数关系吗?”这系列问题以“理解性提问”和“评价性提问”为主[10]，都富有挑战性，提问的受众覆盖面广，为全体学生营建了平等和谐的思维场景，疑问不断提出，又不断被解决，学生的探究欲望被不断激发，在激疑、生疑、释疑的良性循环中，学生的思维自然发展，对二次函数的概念和与其它函数异同的理解有质的飞跃．然而，问题的解决又是获得真知灼见的开始．当学生沉浸在“无疑”的喜悦中时，教师适切提出“这些都是一次函数和二次函数，有没有其它的函数关系呢?”引发学生新的思考，激起新的思维波澜，学生始终处于上下求索的愤悱状态，有助于学生形成不断质疑、释疑的学习习惯，凸显了数学的理性精神．正如张诗亚先生所说：“一惑刚去，一惑又来，如此循环往复、层层深入，促使学习者思维的发展与知识的增进．”[11]《学记》有说：“善问者如攻坚木，其先易难，后其节目．”讲的也是这个道理．

在巩固练习环节，教师基于数学知识内部蕴含的逻辑关系设置问题：当=0时，即是知自变量的值求函数值；当=0时，即知函数值求自变量的值；于物理问题中理解二次函数和一元二次方程的联系，凸显数学的工具性和应用性，也为跨学科发展学生问题意识提供例证．

5 概念延伸 须教有疑

5.1 教学片断呈现

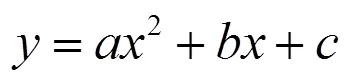
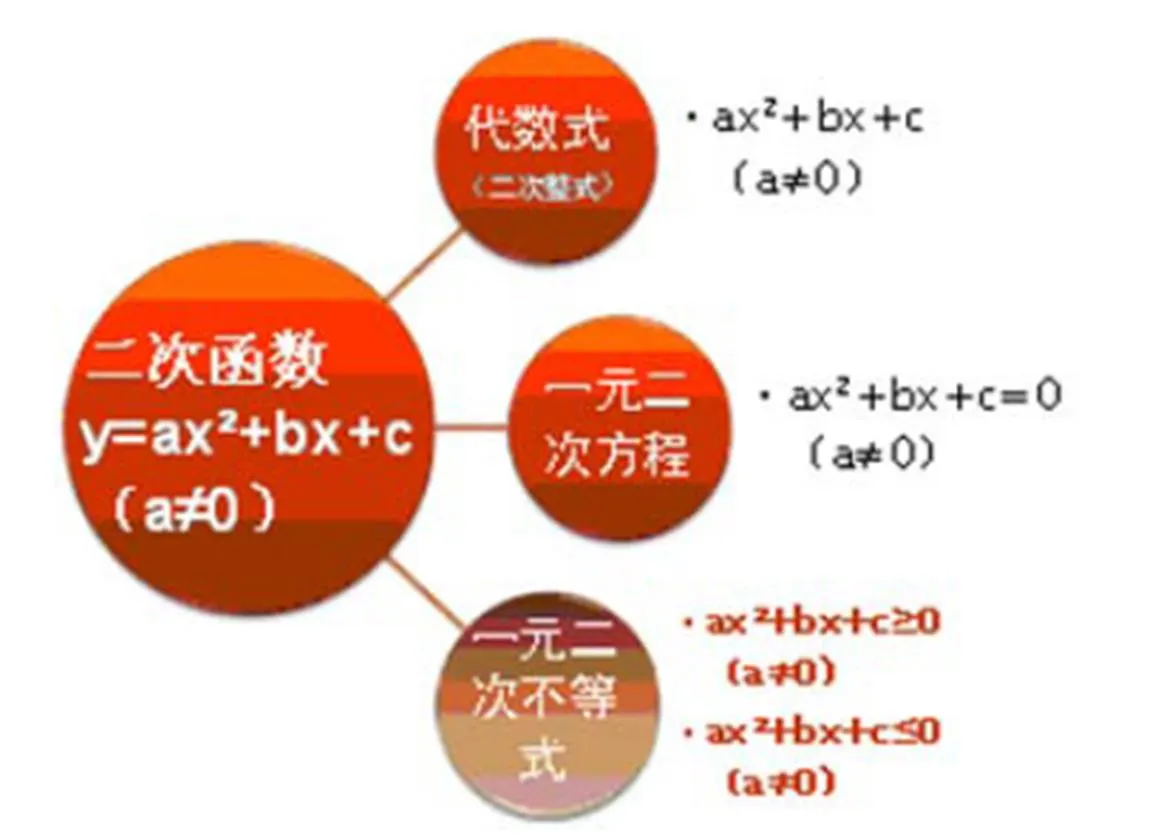
图4

5.2 评析与思考

数学是充满着联系的，不要教孤立的片段，应该教连贯的材料[12]．因此，数学概念教学应帮助学生建立与相关概念的联结，使当前概念与上位概念、下位概念结构化、网络化、立体化，实现新旧概念的无缝对接．二次函数与已学函数，与二次整式、一元二次方程、一元二次不等式，彼此间存在着统一的数学关联，通过课堂导学和小结，既能让学生链接旧知，展望未来学习的相关内容，为学生建构与二次函数相关的数学知识系统提供了“机会和可能”，又给予了学生必要的数学学习方法指导，恰到好处地发挥数学的教育性，让学生适时沐浴数学精神、思想与方法，获得理性的数学思维的教育[13]．让其带着对“已知”的收获与喜悦、对“未知”的好奇与疑问离开课堂，使学生产生“心求通而未得，口欲言而未能”的愤悱之感，进而达到课内向课外延伸之目的，这正可谓“言有尽而意无穷．”这就是数学的内在力量之所在！

总之，学生数学学习的过程是一个持续的“无疑—有疑—无疑”的动态循环和提高超越过程．在这个过程中，教师循“在无疑中发现问题——在生疑中提出问题——在质疑中分析问题——在释疑中解决问题——在无疑中发现新的问题”的程式展开教学，其作用是“教有疑”与“教无疑”：当学生“无疑”时，教师要“须教有疑”，制造“山重水复”的窘境；当学生“有疑”时，教师则要“教而无疑”，不断开创“柳暗花明”的胜景，这便是关于“有疑”与“无疑”的辨证处理要诀，也是“教有疑”和“教无疑”的理想境界．

在具体的教学实践中，教师一方面要在学生的“思维生惑点”[14]设问，注重设问的有效性，从能力与方法上设问，从易错易混角度上设问，从成长点和提高点设问，从开发潜能点上设问[13]．另一方面，教师要从整体规划提问；有效运用元认知提示语；及时分析统整学生的回答；恰当创设疑境，引导学生提出有意义的问题等方面优化课堂设计，培养学生提出问题的能力[15~19]．当然，“疑”有深浅，“问”有大小，教师能否有效地提问和引发学生有效的疑问，源于教师的教学观和学生观，源于教师对课标和教材的理解，源于教师自身的问题意识，源于教师对数学教育的情怀．这也是未来数学教师着力之所在．期待数学课堂在践行中丰腴，在丰腴中实现增值！

[1] 胡小松，朱德全．论数学教学设计的逻辑起点[J]．数学教育学报，2000，9（3）：33-36．

[2] 孙培青．教育名言录[M]．上海：上海教育出版社，1984．

[3] 黄晓学，李艳利．论数学教学设计的创意生成点[J]．数学教育学报，2010，19（6）：9-12．

[4] 赵齐猛．数学课堂教学的逻辑结构[J]．中学数学教学参考：中旬，2013，（1-2）：34-38

[5] 李祎，曹益华．概念的本质与定义方式探究[J]．数学教育学报，2013，22（6）：5-8．

[6] 赵思林，朱德全．试论数学直觉思维的培养策略[J]．数学教育学报，2010，19（2）：23-26．

[7] 赵生初，许正川，卢秀敏．图形变换与中国初中几何课程的自然融合[J]．数学教育学报，2012，21（4）：95-99．

[8] 张奠宙，张荫南．新概念：用问题驱动的数学教学[J]．高等数学研究，2004，（5）：10．

[9] 匡继昌．如何理解和掌握数学概念的教学实践与研究[J]．数学教育学报，2013，22（6）：74-78．

[10] 叶立军，胡琴竹，斯海霞．录像分析背景下的代数课堂教学提问研究[J]．数学教育学报，2010，19（3）：32-34．

[11] 张诗亚．教学中的以“惑”为诱[C]．南京：南京师范大学出版社，2010．

[12] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平译．上海：上海教育出版社，1999．

[13] 王光明．高效数学教学行为的特征[J]．数学教育学报，2011，20（1）：35-38．

[14] 黄晓学．论思维生惑点与数学教学[J]．数学教育学报，2007，16（2）：16-19．

[15] 温建红．论数学课堂预设提问的策略[J]．数学教育学报，2011，20（3）：4-6．

[16] 王光明，宋金锦，佘文娟，等．建立中学数学英才教育的数学课程系统——2014年中学英才教育数学课程研讨会议综述[J]．课程·教材·教法，2014，（5）：122-125．

[17] 李鹏，傅赢芳．论数学课堂提问的误区与对策[J]．数学教育学报，2013，22（4）：97-100．

[18] 曹一鸣．数学教学中的“生活化”与“数学化”[J]．中国教育学刊，2006，（2）：46-48．

[19] 温建红．数学课堂有效提问的内涵及特征[J]．数学教育学报，2011，20（6）：11-15．

Discovering and Solving Problem——The Teaching Observation of Excellent Classroom Model: The Conception of Quadratic Function

TANG Fen1, ZHU De-quan2

(1. Yongchuan Middle School, Chongqing 402160, China; 2. Faculty of Education, Southwest University, Chongqing 400715, China)

The process of math study is the process of the circulation and transcendence of problem-discovering and problem solving .What teachers should do is to teach students how to pose question and then solve it; the aim of teaching is leading students into question which are ignored and solving the problem asked by them. Teaching students how to pose question and then solve it not only the dialectical treatment, but also the ideal state.

problem discovering; problem solving; question; conception; quadratic function

2014–07–21

中国基础教育质量监测协同创新中心项目——数学素养体系构成与质量监测研究（ZJXT201402）

唐芬（1973—），女，重庆永川人，中学高级教师，主要从事中学数学教育教学研究．

G421

A

1004–9894（2014）06–0068–05

[责任编校：周学智]