初中数学实验的心理功能

谭顶良



初中数学实验的心理功能

谭顶良

（南京师范大学 心理学院，江苏 南京 210097）

数学实验是数学课程改革所倡导的新的学习方式，它改变了人们对数学学科性质及教育价值的认识，符合人类认识事物的一般规律和脑科学的基本原理，也兼顾到不同学习者的个体差异和性别特征，对数学教育目标的达成和学习成效的提升具有独特的心理功能．

初中生；数学实验；教育价值；心理功能

传统教育观念认为，数学学习就是学生动脑思考、接受理解老师所讲知识的过程．然而，现代教育学、心理学研究表明，教师在课堂上单纯地讲授一些科学知识不是真正的教育，只有让学生自己经过实际调查和亲身动手操作，才能促使学生掌握科学的方法，建构自己的知识，并获得相应的情感和态度体验．因而，学生除了要认真听讲、积极思考外，还应将动手实践、自主探索、合作交流等也作为数学学习的重要方式．

早在20世纪60年代，日本从小学开始就为数学学习配备了六十余种学习用具，包括操作用具（如木方块、数字卡片、计算卡片、小棒、钉子板、几何图形、钟表模型等）、仪器、教学挂图等，为学生通过“动手做”的方式学习数学提供必需的物质保障．

美国科学家在教育大师杜威“做中学”教育主张的基础上，总结出一种新的教育思想和方法——“hands-on”，旨在让学生用科学的方法学习知识，美国Glencoe/Mc Graw-Hill公司2002年出版的中学数学教材专门开设了“hands-on”版块，展示了这种新的教育思想和学习的方法[1]．

法国著名物理学家、诺贝尔奖获得者乔治·夏尔帕1994年访问美国学校时，深受其“动手做”（hands-on）教育的启发，并萌发了在法国学校开展“动手做”计划的设想．1996年，十多名法国顶尖科学家和教育家共同协商并推出“动手做”（LAMAP）教育计划．从此，“动手做”成为法国教育的一个亮点，在教育改革的道路上形成了自己的特色[2]．

2011年，中国义务教育数学课程标准将数学实验作为学生学习数学的重要方式之一，强调学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程．所谓数学实验，是指为获得某种数学理论，检验某个数学猜想，解决某类数学问题，实验者运用一定的物质手段，在数学思维活动的参与下，在一定的实验环境或实验条件下所进行的一种数学探索活动．它是通过动手动脑“做”数学的一种数学学习活动，是学生运用有关工具（如纸张、剪刀、模型、测量工具、作图工具以及计算机等），在数学思维活动的参与下进行的一种以人人参与的实际操作为特征的数学验证或探究活动[3]．

数学实验与传统的数学教学的主要区别是，传统的数学教学注重知识的传授和逻辑推理能力的培养，而数学实验则侧重于引导学生用形和量的观念去观察和把握现象，培养学生综合运用数学知识分析和解决问题的意识与能力，即数学素质．数学实验作为一种新颖的学习方式，改变了人们对数学学科性质与教育价值的认识，符合人类认识事物的一般规律和脑科学的基本原理，也兼顾到不同学习者的个体差异，对数学教育目标的达成和学习成效的提升具有独特的心理功能．

1 数学实验符合学生认知与学习的基本规律

学生在校学习的内容，大多是人类社会千百年来积累起来的社会文化历史经验，在认识论中属于间接经验，但间接经验的掌握必须以学生自身的直接经验为支撑．而直接经验的获取则依赖于学习者的探索尝试、操作实验等外在活动．

数学是一门抽象度极高的学科，学好这一学科，更需要学习者具备直接经验的基础．在以往的数学学习中，总有部分学生难以理解抽象的数学概念和原理，学习成效低，甚至失去数学学习的信心．究其原因之一，或许就是因为数学教学方式过于抽象，与学生认知学习规律及心理特征不相吻合．过于抽象的内容，会使学生觉得与社会生活实际较为遥远、没啥用，从而难以体现其价值与作用．针对这一现象，新课标特别强调，数学教学应根据具体的教学内容，注意使学生在获得间接经验的同时也能够有机会获得直接经验，以体现其应用性及与社会生活的联系及价值．数学实验刚好能够为学生提供这方面的直接经验．

建构主义学习理论认为，学习不是学习者被动接收信息刺激，而是基于自己的经验背景，对外部信息进行主动选择、加工和处理，从而建构并获得意义的过程．抽象地说，外部信息本身没有什么意义，意义是学习者通过新旧知识经验间反复的、双向的相互作用而建构成的．这一建构过程，既表现为学习者外部的动手操作、探索实验，也表现为其脑中内部的认知过程．而内部的认知过程必须基于外部的操作过程才得以实现．

皮亚杰认为，知识不是来自先天的遗传，也不是来自后天的环境，而是来自主体的行动（action）．主体为了认识某一事物，首先必须操弄它、改变它、转换它，即对该事物采取行动．从最基本的感觉运动（如吸吮、吞咽、抓握）到复杂的思维活动（如排序、组合等），知识的发生与发展始终与行动联系在一起．行动不仅是知识的源泉，更是主体建构知识的首要条件．运算是由行动内化而成的抽象思维活动．当主体由感觉运动阶段过渡到运算阶段时，行动便内化为运算．此时，主体在其头脑里即可进行理性思考而无需借助于实物操弄．如果学习内容难度过大、过于抽象时，则仍然需要学习者借助具体的操作行动才能掌握．这是皮亚杰所揭示的认知发生的一般规律．

美国教育心理学家大卫·库伯在总结约翰·杜威（John. Dewey）、库尔特·勒温（Kurt. Lewin）和皮亚杰相关理论的基础上提出了体验式学习（experiential learning）模式，也叫体验式学习圈理论．他认为，学习不是内容的获得与传递，而是通过经验的转换从而创造知识的过程．体验式学习经历具体体验、沉思观察、抽象概括、主动实践4个紧密相扣的环节构成．具体体验是学习者基于原有的知识经验对当下进行的学习产生相应的情感体验；沉思观察是学习者从多个角度观察、理解事物并进行深入思考；抽象概括是学习者将所观察理解的内容通过理性思维进行形而上的提升与概括，使之成为合乎逻辑的概念或原理；主动实践，学习者将掌握的概念或原理运用到制定策略、解决问题的实际行动之中．

数学实验帮助学生积累基本活动经验、为学生提供丰富多彩的学习素材，在感性认识的基础上进行归纳、概括、抽象、推理等理性活动，因此数学实验这种由外而内的学习过程，符合学生认知与学习的基本规律．

2 数学实验使人脑各区域及左右两半球功能得以充分发挥

人的大脑皮层负责高级的认知和情绪情感活动，它由额叶、顶叶、枕叶和颞叶4个区域组成，分别有着不同的功能：颞叶以听觉功能为主，听觉中枢位于颞上回和额中回之间；枕叶以视觉功能为主，视觉中枢位于枕叶的枕极；顶叶以身体感觉功能为主，中央后回是躯体感觉中枢；额叶以躯体运动功能为主，中央前回是运动中枢．大脑皮层除上述感觉区和运动区以外，还有起联络、综合作用的结构和机能系统，称为皮层联合区，它占据整个皮层的一半位置．联合区不直接与具体的感觉过程和运动过程相联系，它的主要功能是整合来自各感觉通道的信息，对输入的信息进行分析、加工和储存，并支配、组织人的言语和思维，规划人的目的行为，调整意志活动，确保人主动而有条理地行动．

以往的数学学习，学生主要倾听教师讲授或观看板书或自己阅读课本，通过眼睛看、耳朵听的方式进行学习，较多地利用了枕叶和颞叶的视听功能，而数学实验充分发挥了顶叶与额叶的驱体感觉与驱体运动功能，实验过程中多感官的协同作用又使皮层联合区的功能得到唤醒与激发．这就使大脑皮层各个区域各个部位的功能发挥得更加充分，从而大大提高学习的成效．

人的大脑还可分左右两半球，它们的分工各有侧重（见表1）．大脑左半球的主要功能是进行逻辑推理和语言表达，右半球的主要功能是进行空间和形象思维，具体的体现为直觉、节奏、形象、想象、空间感、整体综合等方面的能力．现代科学研究表明，右脑功能的开发和利用，对整个大脑的协调，促进思维的广度和灵活性将有积极的意义．

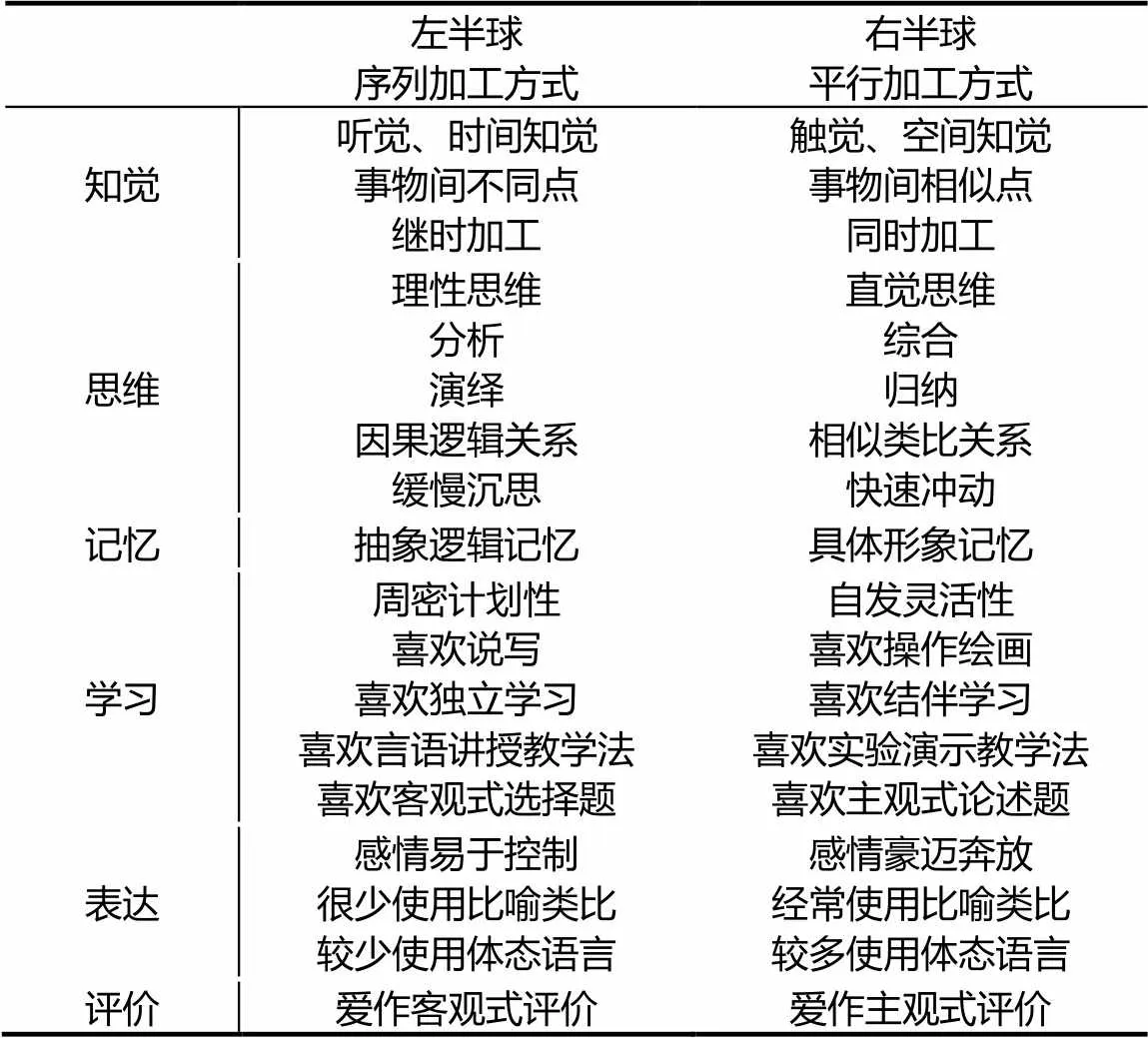
表1 左右两半球加工方式及其一般特征

由于较多地强调其理性、抽象、系统和逻辑，传统数学学习的方式较多地使用大脑的左半球，所以导致那些偏爱右脑思维的“右脑人”难以胜任数学学习任务，学习成绩相对较差．数学实验通过触觉、空间知觉、归纳、类比等直觉思维和具体形象思维及动作记忆等认知活动，使原本在数学学习中较少有用武之地的右半球功能得到有效的发挥．在数学实验的过程中，学习者将右半球的直觉与左半球的理性有效融合，激活了全脑思维．例如，在探究递归数列的通项公式时，首先让学生尝试计算数列的前几项，然后观察、分析前几项的特征，这时学生的左脑处于积极活动状态并起着主导作用；接着，通过一些思考和探究，突发性地或偶然地发现了通项公式的规律，就得到了猜想，猜想的获得主要依靠右脑的直觉思维；最后，学生用数学归纳法或其它方法证明猜想的正确，这需要左脑的逻辑思维．可见，求递归数列的通项公式，既需要左脑的逻辑思维，又需要右脑的直觉思维[4]．左右两半球功能的协同作用能使所有学习者的数学学习成效得到更大的提升，尤其能使原来那些数学“学困生”的面貌发生根本性的转变．

3 数学实验符合初中生心理发展的年龄特征及个体差异

小学生的思维以具体形象思维为主要形式，到了初中阶段，则逐步过渡到以抽象逻辑思维为主要形式，但他们的抽象思维水平仍然较低，处于从经验型抽象向理论型抽象思维的过渡阶段，其逻辑思维层次在很大程度上仍处于形式逻辑思维阶段，辩证思维还只是处在萌芽和初始状态，他们对数学知识的理解、判断、推理在很大程度上仍然离不开直观形象的支撑．因此，运用数学实验，可以引导学生通过动手操作、探索实验的方式积累感性经验，为他们理解抽象程度更高的数学知识并促进数学思维发展奠定坚实的基础．

人在成长发展过程中，表现出各不相同的个体差异．数学教学应致力于实现义务教育阶段的培养目标，要面向全体学生，适应学生个性发展的需要，使得人人都能获得良好的数学教育，不同的人在数学上得到不同的发展[5]．

人的个体差异首先表现在认知方式上．周珍等人研究发现，场独立型学生，数学成绩最好，空间图形认知能力最强；场中间型次之；场依存型学生，数学成绩最差，空间图形认知能力最低[6]．

人的个体差异还表现为智力类型的差异．美国教育心理学家加德纳提出的多元智力理论认为，人的智力有逻辑数理智力、空间智力、语言智力、音乐智力、身体动觉智力、人际关系智力、自我调节智力、观察自然智力等因素构成，而当今学校教育注重培养和考察的主要局限于数理逻辑智力、空间智力、语言智力3个方面．其实，身体动觉智力对一个学生当今的学习及未来的发展产生着至关重要的影响．

加德纳认为身体动觉智力是一个人对身体运动的控制能力和对一定对象的熟练操作能力．这种智力突出的人，喜欢体育运动和体育竞赛，而且成绩往往较好，学习时坐不住，与人谈话时手势较多，手工技能较好，容易模仿他人的行为举止．这种学生适合于从事体育、缝纫、木刻、打字、绘画、装配、演员等行业的工作．但这类学生在学校的书面测验分数往往较低，因此会被老师认为是差生，他们在学校教育尤其是在我们东方文化的教育环境中往往得不到充分的重视，学习成绩差，辍学率相对较高．对这种类型的学生，数学学习最好的方法就是调动他们身体运动智力的优势，带动逻辑数理智力和观察自然的智力，引导他们“做中学”或进行数学实验．

人们接受信息、进行学习，借助不同的感觉器官，凭耳朵听、用眼睛看、用双手触摸操作等．因此接受信息的渠道有视觉的、听觉的和动觉的不同方式．据研究，外界的信息有百分之七、八十是通过视觉进入人脑的．在这一大前提下，不同的人对不同的感觉器官和感知通道仍有不同的偏爱，有些人喜欢通过视觉的方式接受信息，也有一些人更喜欢通过听觉了解外在世界，还有一些人更习惯通过动手（或身体运动）来探索外部世界从而掌握信息．有研究资料表明，大约20—30%的学龄儿童习惯通过听觉接受并储存信息，40%的学生喜欢通过视觉，另有些学生则喜欢通过具体的操作活动较为有效地获取知识，还有一些人则属于两种或3种感知觉的结合型．不同感知觉类型的学生，在学习上有着不同的表现，见表2[7]．

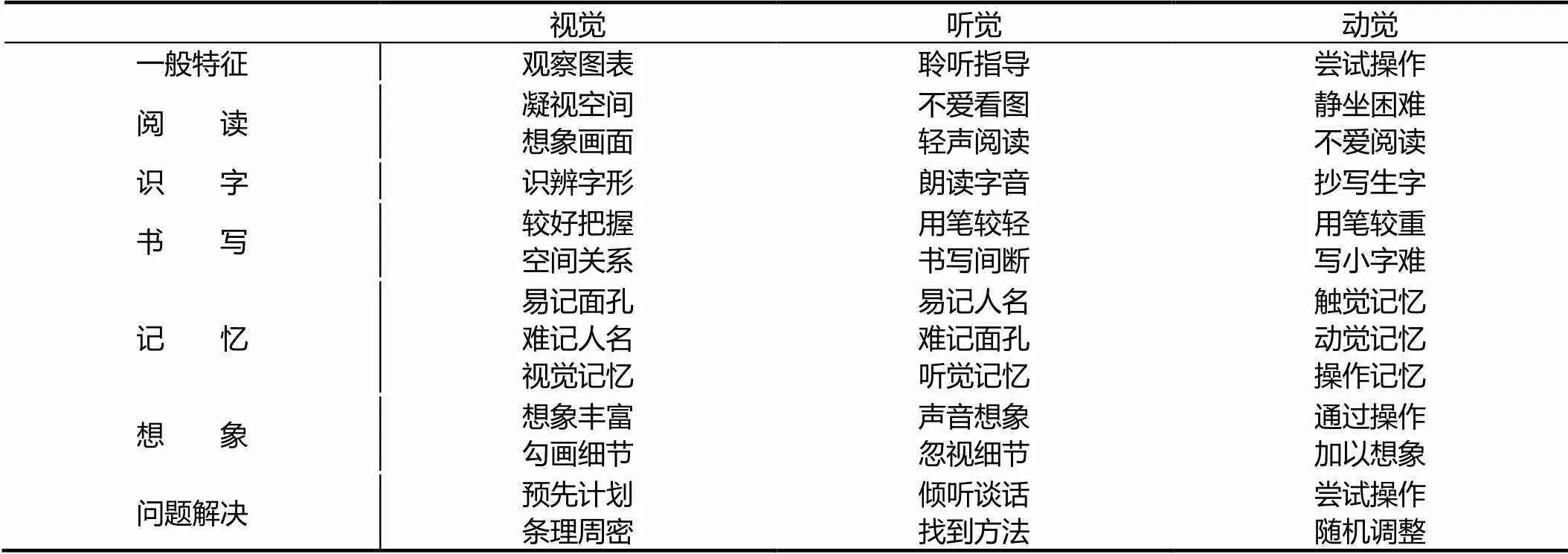
表2 “视听动”3种感知觉类型的认知与学习特征

人的任何一种心理活动，都包含有认知、情感和意志行动3种成分．不同的学习者在其心理活动中，这3个成分所占的比重可能会有所不同，也就是说各学习者对上述3个成分的偏爱不一样，因此在学习上就表现为3种不同的风格类型：理智型、情感型和操作型，在具体的学习过程中会表现出不同的特征，见表3．

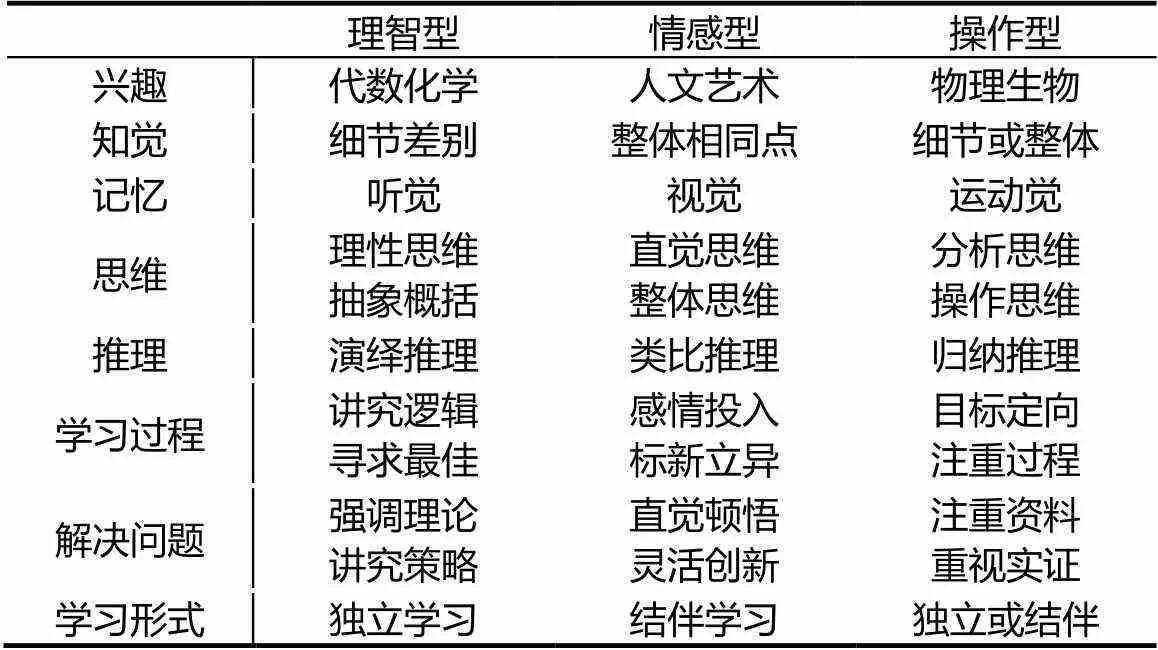
表3 理智型和情感型及操作型学习者的学习倾向与特征

以上所讨论的学生的个别差异，都涉及到“动觉型”．这类学生擅长动手操作而不擅长阅读与倾听，在中国的教育环境及以讲授法为主的教学方式下，无法有效地理解课堂内容．而课后他们通过自己的动手操作掌握的知识，在当今主要通过纸笔测验的考试中又难以得到有效的体现，致使他们往往会成为“差生”甚至“嫌弃生”．这种现象，在数学学习中表现得更为突出．

数学实验这种学习形式，强调学习者亲自动手、尝试探索、收集资料、归纳推理等具体的操作过程，符合动觉型学生的学习特征，满足他们的学习需要，能重新焕发他们已销蚀多时的学习热情，从而有效促进他们的学习成效．

数学实验还照顾了学生的性别差异．男女生在学习数学上存在一定的性别差异，通常表现为男生优于女生．这与男女生各自的性别特征有关．

人的大脑两半球功能是有差异的，左半球主管抽象的言语思维，而右半球则主要处理空间和图像感知能力和非言语思维．男女两性的智力活动在大脑两半球的反应部位及成熟的快慢有所不同．男性抽象概括能力和空间想象能力比女性强，倾向于从全局考虑问题，比较长于逻辑思维和空间思维．而女性则擅长言语类活动，抽象概括能力和空间想象能力等方面相对较弱．

在识记方式上，男女生也有所不同．女生的识记方式带有明显的机械的成分，习惯于“老师讲，自己背”的学习方式，能熟练叙述概念、法则．而男生则倾向于理解记忆，对某些概念、法则只知道基本意思和主要特征，而不能精确地叙述．这两种识记方式对简单知识学习产生的差距不大，但对学习高认知水平内容的影响则非常明显，如学习立体几何时，不少女生能熟练背诵和叙述定理、方法，却难以根据概念、定理画出正确的图形，而男生则相反．这显然与记忆方式有关．

在数学学习过程中，男生爱独立思考，分析问题时比较注重抓主要矛盾和事物间的联系，擅长于抽象思维，但不重视细节；而女生模仿较多，偏重形象思维，抽象概括能力较弱，难以把握事物间的内在联系．男女生这种思维方式的差异对相对容易理解的数学内容影响不大，但对抽象程度和综合程度相对较高的数学学习来说，所产生的影响是显而易见的．相对男生而言，女生囿于自己习惯的思维方式，难以适应数学学习所提出的高要求．周超研究发现，初二女生在计算、概念、领会、分析等方面的表现几乎都呈现出略比男生差的现象[8]．

数学实验顺应女生在感知、思维、记忆和解决问题上的特殊性，注重感性形象、细节把握等，又弥补她们理性思维、整体认知、动手操作等方面的不足，促进他们在数学学习中能与男生并驾齐驱．

4 数学实验是学习方式转变的典型代表也是数学教学目标达成的必要手段

课程改革倡导学习方式应由被动接受式学习向主动探究式学习的转变．关于学习方式的分类，有一些教育心理学家从不同的角度、依据不同的逻辑作了种种不同的尝试．我们根据学生在学习过程中所表现出的主动性、创新性程度，将学习方式区分为机械接受学习、意义接受学习、发现学习、研究型学习4种类型，并组成如图1所示的一个完整序列[9]．

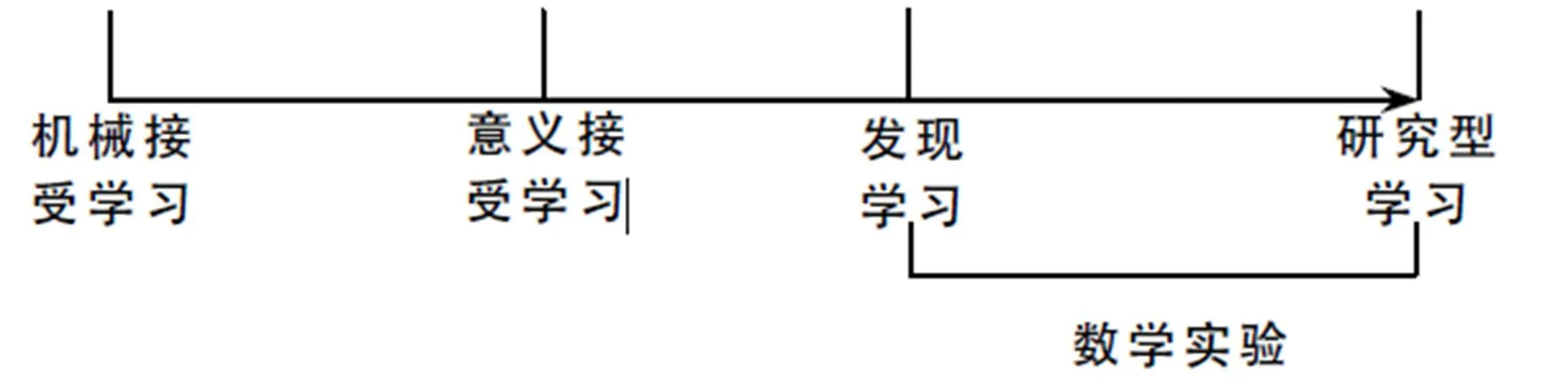
图1 学习方式序列

（1）机械接受学习．学生仅仅是孤立地记住老师或课本呈现的知识或事实细节，而不理解知识的产生过程、意义以及知识之间的相互关系，学习的积极主动性和创新性是最低的，甚至几乎没有．

（2）意义接受学习．学生凭借自己认知结构，理解、接受课本或老师呈现的新知识的意义，并内化到自己的认知结构之中，这种学习方式即为意义接受学习．

（3）发现学习（探究性学习或学科渗透的研究性学习）．知识或问题的答案不由老师直接呈现给学生，而由学生自己探究发现，理解知识的意义及其产生过程，并建构自己的认知结构，这是美国教育心理学家布鲁纳（J. S. Bruner）所极力倡导的学习方式．

（4）研究型学习．针对研究性学习课程所进行的类似于科学家发明创造的学习，需要学习者自己（或成立学习小组）发现问题、收集资料、提出假设、验证假设等一系列探索实验、动手实践的过程．

上述4种学习方式，前两种是接受式的，带有较多的被动性，而后两种是探究式的，带有明显的主动性与创造性．数学实验这种学习方式，介于发现学习与研究型学习这两种学习方式之间．因此，数学实验是学习方式转变的典型代表．

义务教育阶段数学课程，需要达成知识技能、数学思考、问题解决、情感态度4个方面目标[5]．

数学学习包括数学概念、命题、数学思想方法等方面的学习．数学实验引导学生从生活经验和已有的知识背景出发，从现实中寻找实物模型，通过观察实验等手段，形成感性认识，从而掌握数学概念和数学命题；从直观、想象到发现、猜想，然后得到验证，使学生亲历数学构建过程，掌握认识事物、发现真理的方式方法，从而实现知识技能的目标．数学实验让学生通过观察，发现问题、构建数学模型、寻求结果、最终解决问题．学生通过反复的观察实验与思考，逐渐掌握问题中所蕴涵的数学思想方法．同时，学生在积极参与实验中，产生对数学的好奇心和求知欲，体验数学的乐趣，感受数学的价值，并形成认真勤奋、独立思考、合作交流、反思质疑的良好态度与学习习惯，达成数学课程的情感态度目标．此外，通过尝试操作、动手实验等活动，学生积累基本活动经验，将为他们日后学习与生活奠定良好的学科基础．

数学实验要求学习者在学习数学时既动脑又动手，手脑并用，内外互动，从而促进学习效率的提高．心理学研究表明，动觉记忆相对于视觉和听觉而言，效果更好．很多学生有这样的感受：听到的容易忘记，看到的印象不深，唯有在实践中感知、理解、领悟、体验过的才最难忘．

当代认知心理学将知识分为事实性知识、理念性知识（有人也译为概念性知识）、程序性知识和元认知知识（主要为策略性知识）4大类[10]．不同知识的学习，需要不同的学习方式，而各种不同方式所取得的成效各不相同，见表4．可见，对于程序性知识和策略性知识而言，必须采用操作练习和实际应用的方式进行学习，即便是理念性知识，仅通过抽象理解的方式学习，其成效仍受到很大的限制，可见操作实验方式的必要[11~16]．

表4 学习内容和学习方式与学习效果的关系

数学实验要求学习者在学习过程中，不仅动手操作，而且需要“眼到”、“耳到”、“口到”，充分发挥多感觉通道的协同作用．心理学研究表明，多感官通道同时参与学习过程，比只利用单一感知觉通道进行学习的效果好得多．

近些年来，心理学正日益关注人的身体运动参与其中的“具身认知”的研究[17]．这一领域的研究认为，认知是包括大脑在内的身体的认知，是同学习者身体的感觉通道联系在一起的．身体的感觉运动系统在认知过程中发挥了重要作用，认知是通过身体的体验及其活动方式而形成的，身体的解剖学结构与活动方式、身体的感觉和运动体验决定了人们怎样认识和看待世界．换句话说，身体运动参与的认知和情感活动，决定其活动的性质和成效，例如，如果一个人开心，就会微笑，而微笑这种面部表情的活动，又会让他变得更加开心．因而，有理由相信，学习者身体运动参与其中的数学实验，在数学学习成效的提高中一定能发挥其独特的心理功能．

[1] 刘丽颖，黄翔．美国数学教材中的“动手做”[J]．数学教育学报，2005，14（2）：53-55．

[2] 皮凤英．“动手做”——法国科学教育计划[J]．外国中小学教育，2002，（4）：17-19．

[3] 董林伟．初中数学实验教学的理论与实践[M]．南京：江苏科技出版社，2013．

[4] 赵思林．感受的心理过程对数学教学的启示[J]．数学教育学报，2013，22（5）：7-11．

[5] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2011．

[6] 周珍．不同认知方式中学生空间图形认知能力发展与数学成绩关系研究[J]．数学教育学报，2013，22（5）：62-65．

[7] 谭顶良．学习风格论[M]．南京：江苏教育出版社，1995．

[8] 周超．八年级学生数学认知水平的性别差异[J]．数学教育学报，2011，20（3）：59-62．

[9] 谭顶良．学习方式转变：热点冷观[J]．南京师大学报（社会科学版），2004，（1）：62-68．

[10] 安德森．布鲁姆教育目标分类学（修订版）[M]．北京：外语与教学研究出版社，2009．

[11] 张晓磊，郭华光．试论数学实验的数学教育功能[J]．数学教育学报，2003，12（2）：38-40．

[12] 尚春虹．数学实验教学的探索与实践[J]．数学教育学报，2002，11（3）：66-68．

[13] 彭拯，禹辉煌．论数学实验的数学方法论价值[J]．数学教育学报，2005，14（3）：27-29．

[14] 隋鸣，许敏慧．数学实验活动与数学教学[J]．数学教育学报，2004，13（2）：93-95．

[15] 常丽艳．中学数学实验课设计范式及其主体认识分析[J]．数学教育学报，2005，14（2）：47-49．

[16] 侯立伟．信息技术利于数学实验的开展[J]．数学教育学报，2006，15（1）：99-100．

[17] 叶浩生．具身认知：认知心理学的新取向[J]．心理科学进展，2010，（5）：705-710．

Psychological Functions of Mathematics Experiment in Junior High School

TAN Ding-liang

(School of Psychology, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Mathematics Experiment is a new way of learning which Chinese curriculum reform advocated, it changed our perception of the mathematics nature and the awareness of educational value, in line with the general laws of human understanding and the basic principle of brain science, also takes into account individual differences and gender differences in learners, and has unique psychological functions for reaching mathematics educational goals and enhancing its learning effectiveness.

junior high school student; mathematics experiment; psychological functions

2014–06–04

江苏省教育科学“十一五”规划重点资助课题——动手“做”数学：初中数学实验的设计与开发研究（B-a/2009/01/014）；江苏省教育科学“十二五”规划重点资助课题——初中数学实验的理论与实践研究（B-a/2013/02/083）

谭顶良（1962—），男，江苏江阴人，教授，博士，博士生导师，主要从事学习心理与教学策略领域的教学与研究．

G633.6

A

1004–9894（2014）06–0026–05

[责任编校：周学智]