高水平数学教学到底该教什么

李 祎



高水平数学教学到底该教什么

李 祎

（福建师范大学 数学与计算机科学学院，福建 福州 350108）

数学教师的教学水平的高低，首当其冲地体现在对教学内容的把握上．高水平的教师，在教教材中显性知识的同时，能挖掘出其后的隐性知识，教到一些别人教不出来的内容．这些不易教到的隐性知识，就是数学的本质、过程、思想和结构．通过深度挖掘教材中各种数学概念、结论等背后的隐性知识，达到与隐性知识的深度对话，有助于提高数学课堂实效和学生的综合能力．

数学本质；数学过程；数学思想；数学结构

教学研究的基本问题是“教什么”和“怎么教”，前者关乎教学内容问题，后者关乎教学形式问题．教学内容决定教学形式，教学形式服务于教学内容．“教什么”永远比“怎么教”更重要．先进理念首先关乎教学内容，首先要关注“教什么”．

从“教什么”的视角来看，数学教师的教学水平的高低，首当其冲地体现在对教学内容的把握上．低水平的教书匠，只会照本宣科，看到什么就教给学生什么，只是知识的搬运工；高水平的教师，能透过现象看到本质，在教教材中显性知识的同时，能挖掘出其后的隐性知识，教到一些别人教不出来的内容．

这些不易教到的隐性知识是什么呢？概括而言，研究者认为是数学的本质、过程、思想和结构等4个方面．认识到数学教材中蕴含的这些隐性知识，通过深度挖掘和解读教材隐性知识，达到与隐性知识的深度对话，有助于提高数学课堂实效和学生的综合能力．

1 教“本质”

1.1 教数学概念的本质

数学概念是反映数学对象的本质属性的思维产物，所谓本质属性就是该类事物共有和特有的稳定属性，也可以说，本质属性就是事物变化当中保持不变的属性．掌握数学概念的本质，既需要静态的分析其定义形式，更需要在比较、变化等联系性活动中揭示其内涵．

比如，对于复数的本质的把握，必须认识到复数是一种二元数，而实数则是一元数．与把一元的实数看作“单纯的数”相比，二元的复数不仅有数量意义，而且还有方向意义，它是一种“有方向的数”，“数量加方向”是复数的本质属性，这一本质属性可以通过复数的代数表示、三角表示和几何表示来进行揭示．

有一些数学概念的本质，相对比较隐晦，更需要教师努力揭示．比如，在小学和初中阶段，分别学过不同的“距离”：“两点之间的距离”，“直线外一点到已知直线的距离”，“两平行线之间的距离”．那么，距离的本质是什么呢？其实，更一般来看，距离的本质就是“最小值”：图形内的任一点与图形内的任一点间的距离中的最小值，叫做图形与图形的距离．把握住这一本质，高中阶段学习“点到平面的距离”，“直线到与它平行的平面的距离”，“两个平行平面的距离”，“异面直线的距离”的概念时，学生也能做到不教自明．

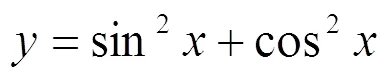
需要说明的是，掌握数学概念的本质，并不意味着背诵概念的定义．比如对于方程的定义“含有未知数的等式叫方程”，并没有反映方程的本原思想．教师在方程定义的黑体字上大做文章，反复举例，咬文嚼字地学习，朗朗上口地背诵，没有实质性的意义．绝对没有学生因为背不出这句话而学不会“方程”的．方程的实质是“为了寻求未知数，在已知数和未知数之间建立起来的一种等式关系”．在数学学习中，学生能否记住方程的定义并不重要，关键在于领会其基本思想，并能够进行灵活地应用[1]．

此外，对于数学概念定义的呈现，并非越严密、越精确，就越有助于掌握其本质，还必须考虑到学生的可接受性．特别是对于抽象程度较高的数学概念，学生接受起来比较困难，这时为了更好地帮助学生掌握概念的本质，需要适度淡化概念的形式定义，以使学生更好地理解概念的内涵．比如在高中数学教材中，对于导数和定积分概念的呈现，便采用了这样的处理方式．

1.2 教数学结论的本质

数学中的结论很多，但大凡列入教材中的重要数学结论，如各种数学公理、定理、公式、法则等，主要在于其经常用到、推证不易、形式简单．把握数学结论的本质，并不在于记诵结论本身，而在于理解其内涵，明确其意义，掌握其功能，认识其成立的理由．

比如在三角形的学习中有许多结论，对每一结论都应尽可能把握其本质：三角形的三内角和定理反映了任意三角形的三内角和所保持的不变性，其正确性在小学可以通过剪拼、折叠或拉伸的方法来进行验证，在初中可以通过平行线的性质定理来进行严格证明；三角形的面积公式本质上是刻画了三角形底边与对应高的乘积的不变性，这一不变量可以度量三角形这一封闭图形的大小，其正确性在小学可以通过剪拼或折叠的方法来进行验证，在初中可以通过三角形的相似来进行证明；三角形全等的判定定理本质上是揭示了唯一确定三角形的大小和形状所需要满足的最简条件；等等．

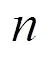
1.3 教数学方法的本质

数学中除了一些结论性知识，还有大量的方法性知识，比如运算的方法、度量的方法、变换的方法、论证的方法等．掌握数学方法的本质，不仅要掌握“怎么做”，即方法运用的程序与步骤，还要掌握“为什么可以这样做”，即数学方法的内涵是什么，不同数学方法使用的条件是什么，适用的范围是什么，数学方法与问题特质具有怎样的关联性．

比如对于数的加、减运算的方法，必需抓住计数单位这一本质．因为自然数以“1”为标准，“1”是自然数的单位，所以任何两个自然数都可以直接相加减．同分母分数，因为它们的分数单位相同，所以能直接相加减；异分母分数，因为它们的分数单位不同，所以就要把它们化成相同的单位，这样才可以相加减．小数的加减运算中，小数点对齐才能相加减，其本质也是相同计数单位要相同．因为只要小数点对齐，相同数位就对齐了，相同计数单位也就同样能相加减了，而不必考虑小数的末位是不是一定对齐．

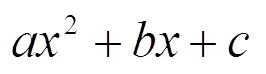
2 教“过程”

数学有3种形态：原始形态、学术形态和教育形态[2]．原始形态是指数学家在探索发现数学真理时所进行的曲折、复杂的数学思考；学术形态是指数学家对探索、发现的数学真理进行归纳、整理形成文本材料后的一种形态，它呈现出的是“简洁的、冰冷的形式化美丽”；教育形态是指教师通过自己的设计，将学术形态的数学知识有效地“激活”，使学生在学习数学时，能够模仿数学家那样进行“火热的思考”，它是介于原始形态和学术形态之间的一种形态．

弗赖登塔尔曾经这样描述数学的表达形式：没有一种数学的思想，以它被发现时的那个样子公开发表出来，一个问题被解决后，相应地发展为一种形式化技巧，结果把求解过程丢在一边，使得火热的发明变成冰冷的美丽，因此他说教材是“教学法的颠倒”．为了彰显数学知识的过程性，通过数学知识的教育形式散发出数学的巨大魅力，让数学“冰冷的美丽”焕发学生“火热的思考”，在数学教学设计中需要采用稚化思维的设计策略．

所谓稚化思维，就是教师把自己的外在权威隐蔽起来，在教学时不以一个知识丰富的教师自居，而是把自己的思维降格到学生的思维水平上，亲近学生，接近学生，有意识地退回到与学生相仿的思维状态，设身处地地揣摩学生的学习水平、状态等，有意识地生发一种陌生感、新鲜感，以与学生同样的认知兴趣、同样的学习情绪、同样的思维情境、共同的探究行为来完成教学的和谐共创．

比如在高中数学教材中，定义了直线的方向向量．为什么要给出这一数学概念？为什么要采用这样的方式来对其进行定义？通过分析与探究不难发现，定义直线的方向向量的根本目的，是为了刻画和确定直线的方向．所谓直线的方向相同，就是指这些直线是互相平行的．那么，为什么不定义直线的“法向量”（与直线垂直的非零向量）？可否用直线的“法向量”来刻画直线的方向呢？回答是否定的，因为一个直线的“法向量”无法确定直线的方向．两个不共线的“法向量”可以确定一个平面，而与平面垂直的直线的方向是确定的．由此可见，用与直线垂直的两个不共线的非零向量也可以表示这条直线的方向，只不过数学追求简洁美，用直线的方向向量只需一个向量就可以了[3]．

通过类似于以上这样的分析和探究，有助于掌握数学知识的产生和形成的客观基础，包括知识的来龙去脉，结论的背景、产生过程和意义，获取知识的方法等．这样不仅可以避免“知其然而不知其所以然”，而且可以有效把握知识的本质和思想方法．

需要说明的是，没有对数学知识的来龙去脉的正确把握，不仅会影响对数学概念发展的认知和理解，也会影响到对具体数学问题的解决．比如，对于题目“求

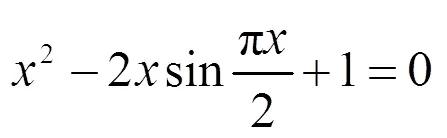
的所有实数根”的求解，当有人在求解中利用二次方程之判别式应大于或等于0时，即

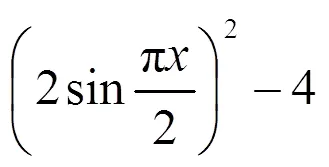
时，许多人对此就会提出“更正”．理由是“原方程根本就不是二次方程”，不能用判别式[4]．产生这一错误认识的根本原因，就在于当人们熟记住了一元二次方程的求根公式之后，许多人忘记了求根公式的来龙去脉，忘记了判别式其实是“配方法的结果”，想当然地认为只有对一元二次方程才能使用判别式非负的性质．

所以教师在引导学生学习知识的过程中，为了凸显知识的本质特征，强化学生的数学理解，就必需重视知识的生成、发生、发展等过程性．掐头去尾烧中段，忽视知识的来龙去脉，有意无意减缩思维过程，就可能造成思维断层，出现严重“消化不良”，这样就会导致学生对知识的表层理解和机械记忆．

3 教“思想”

数学问题可以千变万化，而其中运用的数学思想方法，却往往是相通的．不去领悟数学思想方法，只满足于对知识结论的记忆和解题技巧的掌握，这种“重术轻道”的数学教学，难以培养出有创造力的人才[5]．因为数学知识教学只是信息的传递，而数学思想方法的教学才能使学生形成观点和技能．数学学习的根本目的，就在于掌握这种具有普遍意义和广泛迁移价值的策略性知识——数学思想方法．

所谓数学思想，是指人们从某些具体数学内容和对数学的认识过程中抽象概括出来的对数学知识内容的本质认识．数学方法是指人们在数学问题解决过程中所采取的步骤、程序和实施办法．数学思想是数学的灵魂，是数学内容和数学方法的升华与结晶，它支配着数学的实践活动．数学方法是数学思想的表现形式和得以实现的手段，它为数学思想提供逻辑手段和操作原则．运用数学方法解决问题的过程就是感性认识不断积累的过程，当这种量的积累达到一定程度时就产生了质的飞跃，从而上升为数学思想．若把数学知识看作一幅构思巧妙的蓝图而建筑起来的一座宏伟大厦，那么数学方法相当于建筑施工的手段，这张蓝图就相当于数学思想．

数学教材中蕴涵了丰富的数学思想方法，但这些思想方法往往并没有明确地写在教材上．如果说显性的数学知识是写在教材上的一条明线，那么隐性的思想方法就是潜藏其中的一条暗线．明线容易理解，暗线不易看明．“明线”直接用文字形式写在教材里，反映知识间的纵向联系；“暗线”反映着知识间的横向联系，常常隐藏在基础知识的背后，需要经过分析、提炼才能显露出来．在数学教材里，到处都体现着这两条线的有机结合．在数学教学中，在教显性知识的同时，能否教出隐性的思想，既影响到了学习的效果，又彰显了教师的素质和水平．

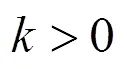
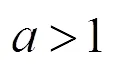
对许多函数性质的研究和探讨，渗透的都是这些思想方法，它们不依内容而异，呈现出某种相通性．这些思想方法看不见、摸不着，要使学生较好地掌握它们：一方面，教师在涉及到思想方法的关键处，要多留出时间让学生进行独立分析和思考，尽可能让他们自己寻找和“发现”这些思想方法，“逼迫”他们在面临问题时学会“数形结合”，学会“分类讨论”，学会“从特殊到一般”等，因为具体函数及其性质仅是学习的载体，通过知识学习掌握这些思想方法、具备这种能力，才是教学的重点和关键；另一方面，教师在教学中要有意识地使用一些提示语，使学生在潜移默化地领会思想方法的同时，尽可能使数学思想方法显性化，使学生对思想方法的学习和掌握，从自发走向自觉，从无意识默会走向有意识习得．

教学中不仅要教宏观意义的思想方法，也要教具体解决问题的思想方法．比如在数学问题解决的教学中，教师在教学时要善于通过“多解归一”的方式，寻求不同解法的共同本质，乃至不同知识类别及思考方式的共性，上升到思想方法、哲理观点的高度，从而不断地抽象出具有共性的数学方法．因为数学知识的巩固主要在于做题，但做数学题不仅要注意“一题多解”，更要注意“多解归一”．“一题”之所以能“多解”，往往就在于这些解法之间是有联系的，这些联系之间是有规律可循的，通过“多解”后的“归一”，让学生能够站在系统的高度看问题，进而升华到从哲学的角度认知世界，这样就可以形成强大的学习能力．

比如对于高中教材中正弦定理的证明，常见的有以下几种不同的证明方法：

（1）作三角形底边上的高线，以高作桥梁进行证明；

（2）作三角形底边上的高线，利用面积法进行证明；

（3）作三角形的外接圆来进行证明；

（4）作三角形的角平分线，根据角平分线定理及角平分线性质定理进行证明．

在具体教学中，究竟讲几种方法为好，常使任课教师感到困惑．其实，问题的关键并不在于方法的多与寡，而更在于能否透过不同解法，挖掘与提炼出更一般的思想方法，即不变量思想和化归转化思想．第一种证法是以高作为不变量来建立等量关系，第二种证法是以面积作为不变量来建立等量关系，第三种证法是以三角形的外接圆的直径作为不变量来建立等量关系，第四种证法是根据角平分线性质定理中的线段相等来建立等量关系．而在以上无论哪种方法的证明过程中，都是通过添加辅助线构造出了直角三角形，利用直角三角形中三角函数的定义建立边与角的关系，而这就是数学中化归转化思想的具体体现．

4 教“结构”

数学家华罗庚先生常说“既要能把书读厚，又要能把书读薄”．读厚，就是要把每一逻辑关系，每一个细节搞清楚，想明白；读薄，就是能抓住课程的主线和基本脉络，抓住课程的内在联系，形成整体认识．

美国教育家布鲁纳也认为，“不论我们选教什么学科，务必使学生理解该学科的基本结构．”所谓学科基本结构，是指该学科的基本概念、基本原理及其相互之间的关联性，是指知识的整体性和事物的普遍联系，而非孤立的事实本身和零碎的知识结论．他认为，这种基本结构应该成为教学过程的核心，因为掌握了学科知识的基本结构，就能把握住知识体系的核心和关键，就可以从宏观上理解学科知识，避免“只见树木不见森林”．

比如，在初中数学教材中，从等角定理（如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补）出发，通过对一个角的一边或两边的平移，与另一个角的边的重合，不难发现这样一个事实，即分散在课本里的6条定义、定理（角相等定义、平角定义、对顶角相等，两直线平行则同位角相等、内错角相等、同旁内角互补），竟全包括在一个等角定理内．这1个定理是那6条定义、定理的联合推广，那6条定义、定理则是这1个定理的特例．因为它们原本是一个系统．

正如数学特级教师孙维刚所言，融会贯通的过程，使人们透过繁杂的现象，抓住了本质，同时简化了记记．更重要的是，接触到了一种崭新的认识问题的思想方法：由寻找联系入手，运用定义、平移变换等数学思想和从“特殊到一般，又从一般到特殊”的方法，把个别的、离散的现象构造成浑然一体的系统，这已经标志着能力的提高和素质的发展了．以这种提高和发展，去学习、去解题，将与过去不可同日而语[6]．

又如，单调性、斜率与导数是3个不同的数学概念，分别在高中不同阶段进行学习．表面看似联系不甚紧密的3个概念，其实存在着内在的本质性联系．

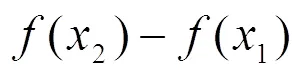
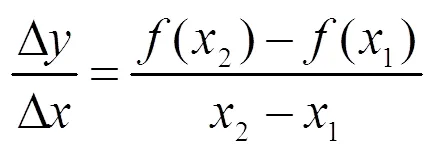
可以看出，只有打通不同知识之间的壁垒，对学科知识体系通晓义理、融会贯通，才能在教学时达到触类旁通、左右逢源的效果．

总之，教师要做到“浅出”，必需先进行“深入”．通过犀利而深邃的数学眼光，透过教材中各种数学概念、公式、定理、法则和图表，看到书中跳跃着的真实而鲜活的数学内容．这些涉及本质、过程、思想、结构等的隐性内容，给人的感觉是“不在书里，就在书里”．此时的教师身上自然散发着一种独特的数学光华与气息，携自身的全部数学涵养融入教室、融入课堂、融入学生，学生由此而汲取数学的丰富营养．

[1] 张奠宙．关于数学知识的教育形态[J]．数学通报，2001，（4）：1-2．

[2] 张奠宙．教育数学是具有教育形态的数学[J]．数学教育学报，2005，14（3）：1-3．

[3] 李祎．基于探究学习的数学教学策略研究[J]．数学通报，2009，（2）：22-24．

[4] 罗增儒．数学解题学引论[M]．西安：陕西师范大学出版社，1997．

[5] 刘茂全．从道家思想看数学教学中的几个关系问题[J]．数学教育学报，2008，17（1）：15-17．

[6] 孙维刚．孙维刚初中数学[M]．北京：北京大学出版社，2005．

High Level of Mathematics Teaching in the End What to Teach

LI Yi

(College of Mathematics and Computer, Fujian Normal University, Fujian Fuzhou 350108, China)

Mathematics teacher’s teaching level firstly reflects on the mastery of teaching content. A high level of teachers can not only teach explicit knowledge in textbook, but also can teach the tacit knowledge in textbook which can’t be mined by other teachers. The tacit knowledge which is not easy to be mined is mathematical essence, mathematical ideas, mathematical process and mathematical structure. A high level of teachers can recognize the tacit knowledge in textbook, and have a conversation with the tacit knowledge which can be acquired by mining mathematical concepts and mathematical conclusions. It is helpful to improve the effect of classroom teaching and students’ comprehensive ability.

mathematical essence; mathematical process; mathematical ideas; mathematical structure

2014–07–10

2013年教育部人文社会科学研究规划基金——数学教师基于教学的学科知识水平发展研究（13YJA880043）

李祎（1971—），男，山西临汾人，教授，博士，博士生导师，主要从事数学教育研究．

G420

A

1004–9894（2014）06–0031–05

[责任编校：周学智]