地震动强度指标与结构地震响应的相关性研究
2014-05-16李雪红李晔暄徐秀丽李枝军
李雪红,李晔暄,吴 迪,徐秀丽,李枝军
(南京工业大学土木工程学院,南京 211816)
地震动强度指标与结构地震响应的相关性研究
李雪红,李晔暄,吴 迪,徐秀丽,李枝军
(南京工业大学土木工程学院,南京 211816)
目前结构抗震分析时使用的地震动强度指标较多,各种地震动强度指标的适用性尚未有统一的定论,缺乏系统的分析。采用考察结构最大地震响应与地震动强度指标之间的线性相关性的方法,选取具有代表性的100条原始地震动记录作为输入,基于不同周期的SDOF系统和实际减隔震桥梁,研究各地震动强度指标与结构地震响应的相关性。根据研究结果,将地震动强度指标划分为4类,其中以Sa(T1)为代表的第Ⅰ类强度指标与不同周期结构的相关程度都较高,而以PGA为代表的第Ⅱ类和以PGD为代表的第Ⅲ类强度指标分别对短周期和长周期结构的相关程度较高,以PGV为代表的第Ⅳ类强度指标相对较稳定,建议采用第Ⅰ类强度指标作为衡量地震动强度的指标参数。并通过工程实例进一步论证了对于自振周期已知的结构,地震动的不同强度指标与结构地震响应的相关性不同。
地震动强度指标;地震响应;相关性
在对工程结构进行动力时程分析时,首先要解决的问题是地震动的选择和调整。由于地震动的随机性,不同地震动作用下结构的内力、位移等响应可能差异很大。目前结构抗震分析及设计时运用比较广泛的地震动强度指标是地震动峰值加速度(PGA)[1]。但近年来的研究和震害经验表明,PGA指标尚不完善,尤其是远场长周期地震动,若采用PGA为强度指标,会夸大此类地震动对结构的影响[2-3]。因此确定合理的地震动强度指标,对正确评价地震动对工程结构的影响具有非常重要的作用。
本文立足于目前主要使用的地震动强度指标,基于单自由度和实际减隔震桥梁,研究地震动强度指标与结构地震响应之间的相关性,分析结构对各指标的敏感性。并结合实际减隔震桥梁,选取包含普通地震动、近远场地震动在内的典型地震动作为输入,进一步分析减隔震桥梁在不同周期地震动下的地震响应以及与地震动强度指标的相关性,为桥梁的抗震性能分析与评价提供地震动输入选择的基础和依据。
1 主要地震动强度指标
在结构抗震分析中,确定一个能综合反映地震动强度大小的指标一直是结构工程抗震研究所面临的难点,也成为实现基于性能抗震设计所需解决的基本问题。目前广泛采用的具有代表性的地震动强度指标主要包括以下几种:
(1)地震动时程峰值。主要包括地震动加速度峰值PGA、地震动速度峰值PGV和地震动位移峰值PGD。其中PGA是目前应用最多的地震动强度指标,大多数国家的规范都是采用这一指标;而PGV比PGA更能表征地震动强度的大小[2];地震动位移峰值PGD多作为对比分析[4]。
(2)地震动反应谱峰值。刘恢先提出采用有阻尼的加速度反应谱的最大值作为地震动强度指标,后来有学者继续推广,提出反应谱峰值表征的地震动强度指标,即地震动加速度反应谱峰值PSA、速度反应谱峰值PSV和位移反应谱峰值PSD[2]。
(3)第一周期谱加速度指标Sa(T1)。Bazzurro等[5]提出了采用结构弹性第一周期对应的有阻尼加速度反应谱值Sa(T1)作为地震动的强度指标。这一指标简单实用,且与传统的PGA强度指标相比大大提高了结构地震响应分析结果的相关性[6]。此外,还有第一周期谱速度指标Sv(T1)和第一周期谱位移指标Sx(T1)。
(4)基于HHT方法的能量指标PIE、PSE。HHT方法可以求出地震动每个时刻的瞬时能量IE(t),其实质是将各个时间点上的Hilbert谱幅值对频率积分,以表达该时刻的瞬时能量,将所有时间点上的瞬时能量的最大值定义为PIE,如式(1),并将其作为地震动的强度指标。此外,可以将Hilbert谱累积能量PSE作为衡量地震动大小的另一个指标,如式(2)。
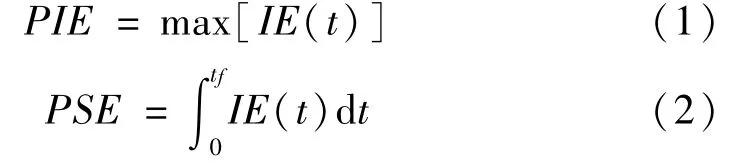
式中,IE(t)为地震动t时刻的瞬时能量,tf为地震动总持时。
(5)谱强度Sa(0-2)、Sa(2-10)。文献[7]针对长周期地震动的特点指出,长周期地震动的加速度反应谱在大于2 s的范围内幅值较大,提出2个谱强度Sa(0-2)、Sa(2-10)作为地震动强度指标,如式(3)和式(4):
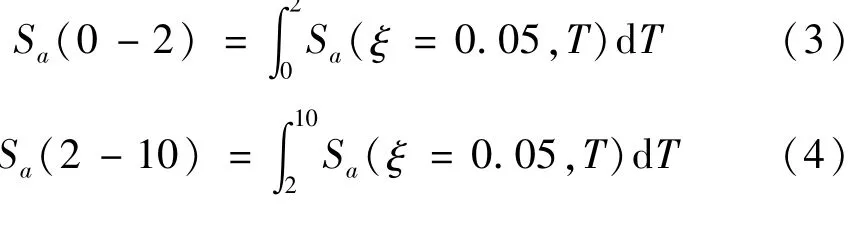
2 地震动强度指标的敏感性分析
以上各种地震动强度指标的适用性尚缺乏系统比较。本文分别以SDOF系统和减隔震桥梁系统的最大地震响应指标Rep来考察其对地震动强度指标I的敏感性,由此对地震动各强度指标的合理性进行全面评价。
2.1 相关性评价方法
合理的地震动强度指标应能反映结构地震响应指标或损伤指标,本文采用考察结构最大地震响应与地震动强度指标之间的线性相关性的方法对指标的敏感性进行评价,并且全面考虑不同自振周期的结构在不同周期、不同强度、不同场地及不同距离的地震动作用下的地震响应。
具体分析步骤如下:
(1)对于基本周期为T的SDOF结构或减隔震桥梁系统,采用时程分析的方法,计算第i条地震动输入下的结构最大地震响应值Repi。
(2)计算第i条地震动的某一地震动强度指标值,记为Ii。
(3)重复第(1)步和第(2)步,得到所有地震动记录的Repi及其对应的Ii。
(4)将所有地震动的计算结果画在Rep-I坐标系统中,计算得到Rep与I之间的Pearson乘积矩相关系数ρ(此相关系数与结构基本周期Τ对应);
(5)改变结构的基本周期Τ,重复第(1)至(4)步,即可在ρ-T坐标系统中画出一系列计算点。
(6)考虑不同的结构响应指标Rep和不同的地震动强度指标I,重复第(1)至(5)步,可得到一系列相对应的ρ-T关系曲线。
(7)比较不同周期结构或同一周期不同地震动强度指标I之间的相关系数ρ,若ρ越接近1.0,则用该地震动强度指标I来评价对应的结构地震响应指标就越合理。
本文从太平洋地震研究中心数据库选取了100条原始地震动记录进行统计分析。所选取的地震动记录PGA范围为0.05 g~1.157 g,PGV范围为9.1 cm/s~159.0 cm/s,PGD范围为5.51 cm~184.42 cm,传播距离范围为0.24 km~127.26 km,场地类型包含A、B、C、D四种类型(USGS标准),其中A类7条、B类16条、C 类44条、D类33条。因此这100条地震动记录涵盖了不同周期、不同强度、不同场地及不同距离的地震动记录,本文以此为基础对地震动不同强度指标的适用性进行分析。
2.2 单自由度系统的分析
本文选取弹性单自由度系统(SDOF系统)分析,阻尼比取5%,其力-位移关系采用线性模型,周期分别取0.5 s、1 s、2 s、3 s、4 s、5 s和6 s。考察SDOF系统的位移响应、基底剪力、结构动能和地震输入能量与不同地震动强度指标之间的相关性。按照上述评价方法绘制的相关系数随周期的变化曲线如图1所示。

图1 SDOF系统地震动强度指标相关系数随周期的变化曲线Fig.1 Correlation curve of ground motion intensity index with the period of the SDOF system
根据图1地震动强度指标与结构地震反应的相关性的趋势,可将其分为以下四类:
(1)第Ⅰ类:以Sa(T1)为代表,包括Sv(T1)和Sx(T1)。该类指标对不同周期的单自由度结构的相关程度都较高。
(2)第Ⅱ类:以PGA为代表,包括PSA、Sa(0-2)、PIE和PSE。这类指标对短周期单自由度结构的相关性较高,对中长周期特别是长周期单自由度结构的相关程度较低。其中Sa(0-2)与结构地震响应的相关性最高。
(3)第Ⅲ类:以PGD为代表,包括PSD、Sa(2-10)。这类强度指标对长周期单自由度结构的相关程度较高,对短周期单自由度结构的相关程度较低,在1 s-3 s周期之间相关系数上升趋势较明显,3 s~6 s周期之间上升趋势相对较缓,相关性基本满足Sa(2-10)≥PSD≥PGD,其中Sa(2-10)的相关性明显高于该类指标中其他2个强度指标。因此,对于自振周期超过3s的结构可以考虑用Sa(2-10)作为地震动输入的强度指标。
(4)第Ⅳ类:以PGV为代表,包括PSV。该类指标的相关系数随周期的变化幅度较小,基本在0.6~0.9之间变化。在0.5 s~2.5 s周期范围内PSV要比PGV相关程度高,在2.5 s~6 s周期范围内PSV比PGV相关程度低。
从各类指标的对比来看,第Ⅰ类强度指标对不同周期的结构相关程度都较高,第Ⅱ类强度指标对短周期结构的相关程度较高,第Ⅲ类强度指标对长周期结构的相关程度较高,第Ⅳ类强度指标对不同周期结构的相关系数相对较接近。
2.3 减隔震桥梁的分析
由于实际结构并不是理想的单自由度系统,具有多阶模态,且实际地震动是频带较宽的非平稳随机过程,频谱成份复杂,使得实际结构的地震响应要比SDOF系统具有较大的不确定性。因此,在SDOF系统分析的基础上,本文又以三跨减隔震连续梁桥为研究对象,进一步考察地震动强度指标与桥梁结构的地震响应之间的相关性。主要分析纵桥向墩顶位移、墩底剪力、支座位移和支座剪力。
支座采用铅芯橡胶支座,通过改变墩高和跨度的方法,形成一阶自振周期分别为1 s、2 s、3 s、4 s、5 s和6 s的减隔震桥梁。图2为墩顶最大位移、墩底最大剪力、支座最大位移和支座最大剪力与地震动强度的相关系数ρ随结构基本周期的变化曲线。
由图2可知:不同指标的相关系数ρ随周期T的变化规律与单自由度结构体系基本一致。第Ⅰ类指标在不同周期都呈现较好的相关性;第Ⅱ类指标在短周期内相关性较高,在中长周期相对较差,尤其与长周期的相关性很差;第Ⅲ类指标在长周期内相关性较好,与短周期的相关性相对较差;第Ⅳ类指标对各周期结构的相关程度变化较小。
综合上述分析,建议采用适用周期范围广、相关程度较稳定的第Ⅰ类强度指标作为衡量地震动输入强度的指标,并且可根据选用的地震动输入的类型分别选用Sa(T1)、Sv(T1)或Sx(T1)。
对于自振周期较长,超过3 s的结构,亦可以考虑采用Sa(2-10)作为地震动输入的强度指标;而对于自振周期小于2 s的结构可以采用Sa(0-2)作为地震动输入的强度指标。下面通过工程实例进一步分析说明。

图2 减隔震桥梁结构体系地震动强度指标相关系数随周期的变化曲线Fig.2 Correlation curve of ground motion intensity index with the period of the Isolation Bridge system
3 工程实例分析
以宿迁至新沂高速公路上一3×30 m三跨连续梁桥为例,该桥梁采用铅芯橡胶支座减隔震设计方案,每个盖梁上四个铅芯橡胶支座,型号为:LRB600-120-160,屈服剪力为90.2 kN,屈服前刚度为9.061 kN/mm,屈服后刚度为0.697 kN/mm。墩柱为双柱墩形式,墩直径1.5 m,墩高10 m。采用有限元软件进行分析,主梁采用三维梁单元模拟,支座采用LINK单元模拟(考虑了支座的非线性),有限元模型如图3所示。阻尼比c取0.05,前五阶振型的自振特性如表1所示。由表1可知,该桥梁的第一阶自振周期为2.213 s。下面主要对PGA、PGV、PGD、Sa(T1)等几个代表性的强度指标进行分析。

图3 有限元模型示意图Fig.3 Schematic diagram of the finite element model

表1 自振特性Tab.1 Natural vibration characteristics
选取2条常规地震动EL-Centro和Taft、2条近场长周期地震动TCU052和TCU068、2条远场长周期地震动ILA004和HKD129以及TCU084、Loma Prieta地震动作为输入。表2列出了8条地震动的PGA、PGV、PGD和第一周期谱加速度Sa(T1)及纵桥向墩底最大剪力、墩顶最大位移、支座最大剪力和支座最大位移,经对墩柱的能力/需求比进行分析,当地震动较强时,墩柱的能力/需求比小于1,需考虑塑性铰的影响,表中所列数据已经考虑了墩柱的塑性铰的影响;图4绘出了支座剪力随着PGA、PGV、PGD和Sa(T1)的变化规律,墩底剪力、墩底位移和支座位移与之规律类似,限于篇幅,未全部列出;表3列出了不同强度指标与地震响应的相关系数。
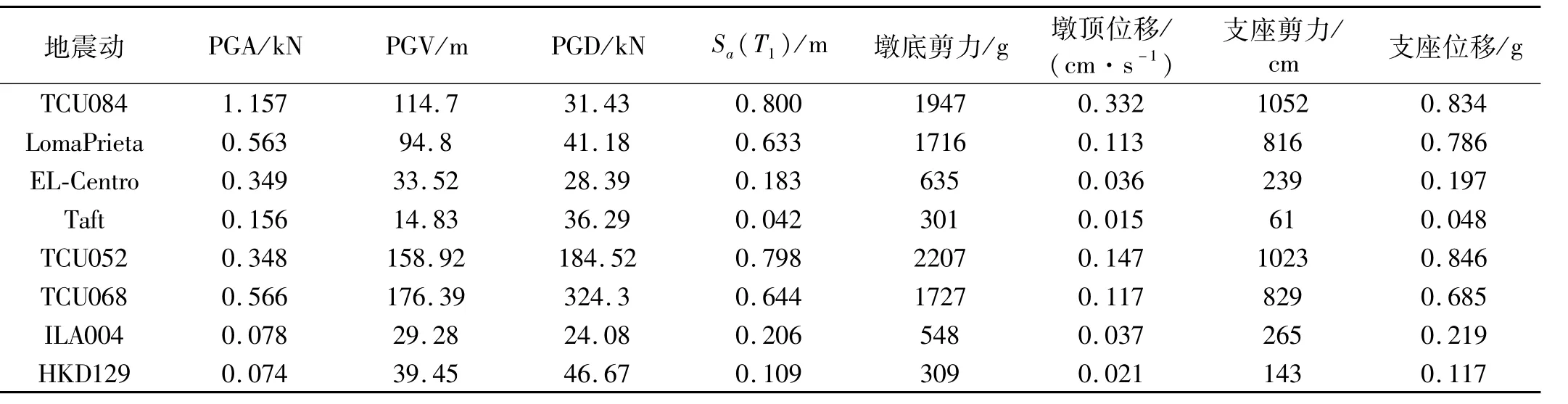
表2 地震动强度指标及地震响应Tab.2 Ground motion intensity and seismic response

图4 支座剪力和强度指标的关系Fig.4 The relationship between bearing shear and ground motion intensity index

表3 强度指标和桥梁地震响应的相关系数Tab.3 The correlation coefficient between bridge structural response and ground motion intensity
从表2、表3及图4可以看出:
(1)地震动强度指标PGA和桥梁结构地震响应的相关系数在0.459-0.628之间,离散性较大。这主要是由于该减隔震桥梁的第一阶自振周期为2.213 s,周期较长,而以PGA为代表的第Ⅱ类指标对中长周期结构的相关性较低所致。
(2)地震动强度指标PGD和桥梁结构地震反应的相关性比PGA要高,相关系数在0.617-0.708之间变化。这是由于PGD指标对长周期结构相关性较高,而当结构的自振周期为2.213 s时,PGD并没有表现出较高的相关性。
(3)地震动强度指标Sa(T1)和PGV与桥梁结构地震反应表现出了较好的相关性,相关系数在0.913-0.976之间变化。
经以上分析可知,对于自振周期已知的结构,不同强度指标表现出了不同的相关性。其中,PGA和PGD受结构自振周期影响较大,PGV和Sa(T1)较稳定。
4 结 论
(1)采用考察结构最大地震响应与地震动强度指标之间的线性相关性的方法,选取具有代表性的100条原始地震动记录作为输入,基于单自由度体系和实际减隔震桥梁,将目前主要使用的地震动强度指标分为4类,依据各指标与结构地震响应的相关程度,通过工程实例对各类指标的适用性进行验证。
(2)以Sa(T1)为代表的第Ⅰ类强度指标,与不同周期结构的相关程度都较高;以PGA为代表的第Ⅱ类强度指标,对短周期结构的相关程度较高,对中长周期结构的相关程度较低;以PGD为代表的第Ⅲ类强度指标对长周期结构的相关程度较高,对短周期结构的相关程度较低;以PGV为代表的第Ⅳ类强度指标随周期的变化幅度较小,相对比较稳定。因此,建议采用Sa(T1)强度指标作为衡量地震动强度的指标参数。
(3)通过对第一阶自振周期为2.213 s的减隔震桥梁在不同特性地震动作用下的地震响应与各类地震动强度指标的相关性分析,进一步论证了对于自振周期已知的结构,不同强度指标表现出不同的相关性。其中,PGA和PGD受结构自振周期影响较大,PGV和 Sa(T1)较稳定。进一步证明了用Sa(T1)为代表的第Ⅰ类强度指标衡量地震动输入的强度是合理的,建议根据所选地震动输入的类型,分别采用Sa(T1)、Sv(T1)或Sx(T1)作为地震动的强度指标。
[1]韩建平,周伟,李慧.基于汶川地震数据的地震动强度指标与中长周期SDOF体系最大响应相关性[J].工程力学,2011,28(10):185-197.
HAN Jian-ping,ZHOU Wei,LI Hui.Correlation between ground motion intensity indices and SDOF system responses with medium-to-long period based on the wenchuan earthquake data[J].Engineering Mechanics,2011,28(10):185-197.
[2]郝敏,谢礼立,徐龙军.关于地震烈度物理标准研究的若干思考[J].地震学报,2005,27(2):230-234.
HAO Min,XIE Li-li,XU Long-jun.Some considerations on thephysicalmeasureofseismicintensity[J].Acta Seismologica Sinica,2005,27(2):230-234.
[3]叶列平,马千里,缪志伟.结构抗震分析用地震动强度指标的研究[J].地震工程与工程振动,2009,29(4):9-14.
YELie-ping,MAQian-li,MIAOZhi-wei.Studyon earthquake intensities for seism ic analysis of structures[J].JournalofEarthquakeEngineeringAndEngineering Vibration,2009,29(4):9-14.
[4]Riddell R,Garcia E J.Hysteretic energy spectrum and damage control[J].Earthquake Engineering and Structure Dynamics,2001,30(12):1791-1816.
[5]Bazzurro P,Cornell C A,Shome N,et al.Three proposals for characterizing MDOF non-linear seismic response[J].Journal of Structural Engineering,1998,124(11):1281-1289.
[6]Vamvatsikos D,Cornell C A.Incremental dynamic analysis [J].Earthquake Engineering and Structure Dynamics,2002,31(3):491-514.
[7]吴迪.长周期地震动特性及其对减隔震桥梁的影响研究[D].南京:南京工业大学,2012.
Correlation between ground motion intensity and structural seismic response
LI Xue-hong,LI Ye-xuan,WU Di,XU Xiu-li,LI Zhi-jun
(College of Civil Engineering,Nanjing University of Technology,Nanjing 211816,China)
Many ground motion intensity indexes are used to the structure aseismic analysis,but there are no unified final conclusion and lack of systematical analysis for the applicability of these indexes.Here,the correlation between ground motion intensity and structural seismic response was investigated by inputting 100 typical ground motion records in to SDOF systems and seismic-isolation-and-reduction continuous-beam bridges having different periods.The results showed that the intensity indexes can be separated into four groups;the group I of indexes represented with Sa(T1)has a higher correlation with structures of different periods;the group II of indexes represented with PGA has a higher correlation with short period structures;the group III of indexes represented with PGD has a higher correlation with middle period structures;the group IV of indexes represented with PGV has a relatively stable correlation with structures.The group I of indexes was suggested to be taken as the ground motion intensity index.A practical engineering analysis showed that different intensity indexes have different correlation with structures having the known natural vibration periods.
ground motion intensity index;seismic response;correlation
U441+.4
A
10.13465/j.cnki.jvs.2014.23.033
国家自然科学基金项目资助(51108234);江苏省自然科学基金项目资助(BK2011803)
2013-08-01 修改稿收到日期:2013-12-24
李雪红女,博士,教授,1974年
