路面板固化翘曲对车辆动荷载和行驶舒适性的影响
2014-05-16胡昌斌孙增华
胡昌斌,孙增华
(福州大学土木工程学院,福州 350108)
路面板固化翘曲对车辆动荷载和行驶舒适性的影响
胡昌斌,孙增华
(福州大学土木工程学院,福州 350108)
路面板由于施工早龄期阶段显著的板顶干缩和凝固温度作用会形成一个始终向上的固化翘曲,基于1/4车辆模型,叠加固化翘曲、环境温度和路面等级对路面随机不平度的共同作用,采用车路动力分析方法研究了固化翘曲对车辆随机动荷载和行驶舒适性的影响。研究表明:固化翘曲对较高平整度等级路面平整度和随机动荷载影响较为显著,主要影响与(板长/车速)相关频率处的路面不平度和车辆随机动荷载参数值。固化翘曲与环境场温度梯度叠加会产生向上或向下翘曲两种情况,面板向上翘曲对路面不平整度和随机动荷载影响较大,向下翘曲则影响很小,但翘曲总体相比路面等级、车辆参数、车速对行车舒适性的影响小。基于该方法可同理分析三辊轴施工形成的更小尺度面板不平整波影响,分析表明该不平整波激振影响的基频值更高,比面板翘曲影响更显著。建议施工尽量控制面板固化翘曲与环境温度组合温度差在-10℃以下,避免辊轴波的出现。
水泥混凝土路面;固化翘曲;不平度;车辆动荷载;舒适性
近年国外研究发现,夏季或干燥地区施工的水泥混凝土路面,由于施工早龄期显著的板顶干缩和凝固时对应高的正温度差(板顶比板底温度高),板会形成一个始终向上的固化翘曲[1-2]。同时固化翘曲现象在各种地理位置和气候条件下都可能存在。
固化翘曲的形成和性状会受到诸如:①施工时段、外部气候环境;②热膨胀系数、热传导率、渗透性等材料性质;③集料类型、水灰比、外加剂、水泥含量等混合料设计参数;④路面结构形式、约束水平等系列因素的影响,具体路段将会显著不同。这种翘曲会导致距板边几英尺范围内板与基层脱开[3-5],特别是重载下会导致裂缝、错台增加、平整度下降、诱发过早破坏[3,6]。
要建立一个有效的固化翘曲理论综合计算模型,需考虑材料、面板结构、混凝土施工前和施工中的环境等多种因素的综合耦合影响,十分复杂[7]。目前研究中为描述固化翘曲,往往剥离引发面板翘曲的环境温度梯度分量,将另外四个分量作用效果等效为线性分布的有效固化温度差EBITD(Effective Built-in Tempera-ture Difference)代替[6]。
近几年国外学者主要通过对不同地区,特定结构和约束条件的足尺路面板的施工观测,并结合相关室内试验,进行路面固化翘曲早龄期形成机制和有效固化温度差(EBITD)反算研究。文献[7]汇总了美国近年基于各类试验获得的沿板厚的等效固化温度差值EBITD[6],在-5~-22.7℃之间(换算成梯度为-20~-90.8℃/m),与我国公路水泥混凝土路面设计规范[8]推荐的最大环境温度梯度标准值域相当,如果再叠加环境场引起的温度差或者翘曲变形将十分显著,形态也十分复杂。
由于研究时间短,目前固化翘曲对路面性能的影响机制研究目前还主要集中在静力定性分析和理论验证解释方面,对于此类翘曲对路面板引起的车辆动力特性变化,和因之而带来的车辆动荷载和舒适性改变,目前仍未得到揭示。鉴于此,本文采用车路动力相互作用分析方法,基于Fourier逆变换法,综合考虑早龄期固化翘曲、环境场温度场和路面等级对路面不平度的影响,采用1/4车辆振动模型开展了固化翘曲对车辆随机动荷载和行驶舒适性的影响研究。
1 面板翘曲对路面不平整度的影响
在众多路面不平度的数值模拟方法中,有线性滤波白噪声法、三角级数法、AR和ARMA法、Poisson法、离散时间随机序列生成法和Fourier逆变换法,Fourier逆变换法思路明确、操作简洁,且计算速度快,模拟精度高,能与给定的功率谱密度一致[9-10]。因此本文首先基于Fourier逆变换法得到路表面随机不平整度,然后叠加考虑早龄期固化翘曲、环境场温度场引起的翘曲得到考虑面板翘曲的路面不平度。
1.1 路面不平度模拟
Fourier逆变换法根据路面不平度功率谱密度分别求出频谱的幅值和随机相位,然后通过Fourier逆变换得到路面不平度的时域表示。
路面不平度的特性可用功率谱密度函数(PSD)Gq(n)来表示[9],根据GB7031-86的分级方法,将路面按照功率谱分成八级,从A级到H级路面不平度状况越低。
车-路系统受到的随机路面不平度激励应考虑车辆行驶速度υ的影响。根据在时间频率f1<f<fu内随机路面不平度的时间功率谱密度Gq(f)与其空间功率谱密度Gq(n)的关系,根据波长与车速和周期的关系,可以得到相应等级路面不平整度功率谱与时间频率的关系。在路面等级、车速已知情况下,给定离散频率fk(k=0,1,2,…,N-1),就可以得到离散的路面不平度时间功率谱密度Gq(fk),进而可通过Fourier逆变换得到路面不平度的时序样本。
本文采用MATLAB软件对不同车速条件下A~D级路面不平度进行了模拟。模拟时,时间频率下限fl和上限fu分别取0.5 Hz和30 Hz[11],这个频率范围能把悬挂(车身)质量部分的固有频率1~2 Hz和非悬挂(车轮)质量部分的固有频率10~15 Hz有效的覆盖在内。车速v可取10 m/s~35 m/s若干数值。
1.2 面板翘曲对路面不平整度的影响
将计算得到的路表面随机不平整度叠加固化翘曲和环境场引起的翘曲变形,可得出考虑面板翘曲的不平整度。面板翘曲依据EverFE2.24水泥路面三维专用程序计算。路面板结构和参数如表1。

表1 路面结构模型计算参数Tab.1 Calculation parameters of pavement structure model

图1 路面在温度翘曲下的不平整度Fig.1 Roughness of slab curling under temperature difference
图1给出了不同翘曲温度差下面板板边翘曲量级。从图可以看到正的温度差(板顶高于板底)造成的面板翘曲成凸形,负的温度差造成的面板翘曲成凹形,且正温度差造成的面板翘曲量级明显小于负温度差。-30℃温度差可导致面板板边相比板中向上翘起3 mm。
根据对EBITD取值问题的已有研究可知,EBITD值在-5~-22.7℃,而我国不同地区路面服役阶段沿板厚温度差值在-5~15℃之间。早龄期固化翘曲与服役阶段温度场共同作用下路面的翘曲温度差在-30 ~10℃之间。正的温度差(板顶高于板底)造成的面板翘曲成凸形,负的温度差造成的面板翘曲成凹形,由于板底支承作用且正温度差造成的面板翘曲量级将明显小于负温度差。
图2分别列举了考虑面板翘曲前后A级(平整度系数几何均值16×10-6m2/m-1)和D级(平整度系数几何均值1 024×10-6m2/m-1)路面不平度的模拟结果和叠加面板翘曲温度差-30℃的结果。从图可以看出路面板翘曲对高等级路面(原始平整度良好)的不平整度影响较明显,但随随着路面等级降低,由于面板表面随机不平整度变异不断加大,翘曲的影响显著性降低,从路面不平整度的量级可以看到,A级路面最大波动值为8 mm左右,而D级路面达到了60 mm,对D级路面(原始平整度很差)基本看不出翘曲对不平整度的影响。这说明面板翘曲量级与路面不平整度波动值的比例,很大程度影响了路面不平整度对面板翘曲的敏感性。

图2 路面板翘曲对不同等级路面不平整度模拟值的影响Fig.2 Effect of slab curling on different level roughness
1.3 面板翘曲对路面不平整度功率谱的影响
图3给出了考虑计算温度梯度差为-30℃的面板翘曲对A级和D级路面不平度时间功率谱的影响,图4为不同行车速度下面板翘曲对A级路面不平度时间功率谱密度的影响。
分析发现,相同面板翘曲对路面等级较高(平整)的不平整度影响更显著,且影响情况与行车速度有关。从图3可以看出,考虑面板翘曲后的路面不平整度的时间功率谱密度(不平整度系数)仅在时间频率为4 Hz,8 Hz,…,28 Hz附近时存在波动,且该波动现象随着路面等级的降低,呈减弱趋势。分析波动部分路面不平整度功率谱密度对应的频率(4 Hz,8 Hz,…,28 Hz)发现,该频率值正是车辆以72 km/h速度行驶在板长为5 m的路面上的频率(4 Hz)的倍数[12]。

图3 面板翘曲不同等级路面不平整度的影响Fig.3 Effect of slab curling on different level roughness

图4 不同车速下面板翘曲对A级路面不平度的影响Fig.4 Effect of slab curling on level-A roughness under different speed
进一步总结发现,不平整度功率谱波动时对应于的频率与板长和车速有关。若行车车速为v,翘曲路面板长为L,面板翘曲对不平度功率谱密度产生最明显影响对应于的频率为1/(L/v)。如当车速为36 km/h时,不平整度功率谱波动时对应于的频率为2 Hz,4 Hz,…,2n,…波动最显著处的频率为2 Hz,此频率正好是车速36 km/h通过5 m板长的频率值。对于车速为72 km/h时,不平整度功率谱波动时对应于的频率为4 Hz,…,4n,…波动最显著处的频率(基本频率)为4 Hz。车速为108 km/h时,不平整度功率谱波动时对应于的频率为6 Hz,…,6n,…波动最显著处的频率(基本频率)为6 Hz。
对比不同车速下相同面板翘曲对路面不平整度功率谱的影响(图5(a)和图6(a)~(b)),车速分别为36、72、108 km/h时的基本频率处不平度功率谱密度值相比于理论值分别改变了2.41、5.21、6.46 mm2·s,说明车速越大,相同面板翘曲量对路面不平整度的影响越显著。
2 考虑面板翘曲影响的随机动荷载
2.1 车辆随机动荷载数值模拟工况
基于1/4车辆振动模型[13],采用Matlab数值程序模拟不同平整度下车辆随机动荷载。重载车辆模型选择Lu Sun模型[14],表2为车辆模型参数及其取值。表3为路面和路基的参数取值。表4为计算随机动荷载计算工况。

表2 车辆模型参数Tab.2 Model parameters of vehicle

表3 路面、路基模型参数Tab.3 Model parameters of pavement structure

表4 随机动荷载计算工况Tab.4 Calculating condition of random dynamic load
2.2 面板翘曲对车辆随机动荷载的影响
图5为不同等级路面面板翘曲对后单轴车辆的随机动荷载的影响。车辆以不同车速行驶在A级路面翘曲面板上产生的随机动荷载见图6(a)~(b)。图中动荷载为后单轴标准轴重货车下得到的。

图5 面板翘曲对后单轴车辆的随机动荷载的影响Fig.5 Effect of slab curling on dynamic load
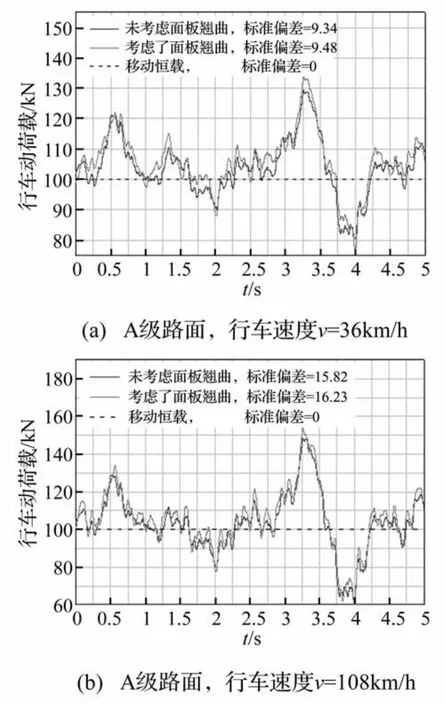
图6 后单轴车辆在不同车速下的随机动荷载的影响Fig.6 Effect of slab curling on dynamic load under different speed
从图5和图6可以看出,面板翘曲对车辆随机动荷载存在影响,且面板翘曲对在平整的高等级路面上行驶车辆动荷载的影响更为明显。
表5给出了不同动荷载计算工况下随机动荷载模拟值的对比,模拟车辆轴重为100 kN。可以看到,考虑面板翘曲后,车辆随机动荷载的最小值变小,而最大值增大,动荷载的标准偏差(均方差)增大,这说明了考虑面板翘曲使随机动荷载的离散性增大。同时,随着路面等级降低,车辆的随机动荷载波动范围增大,离散性增大。
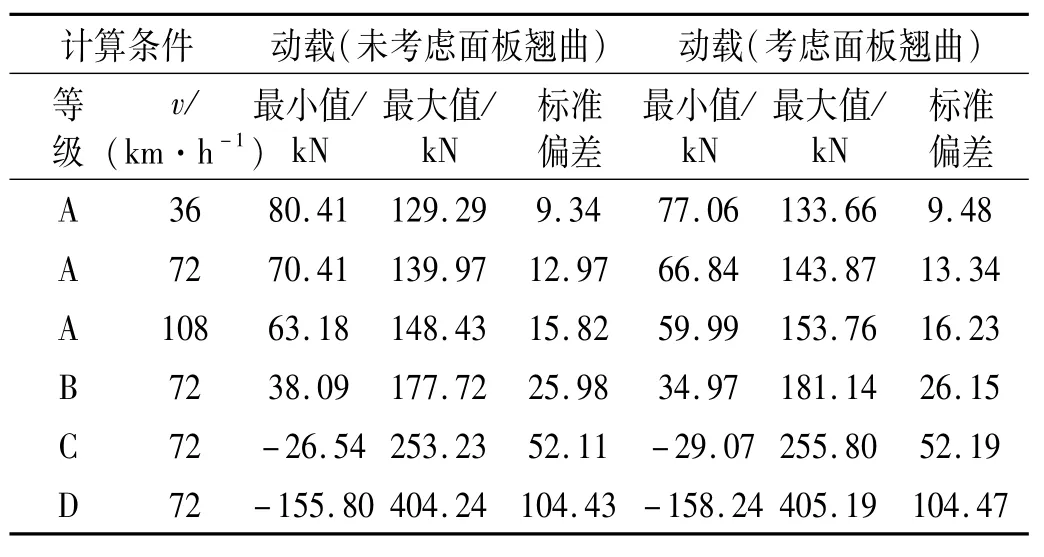
表5 面板翘曲对随机动荷载的影响Tab.5 Effect of slab curling on dynamic load
对比相同路面等级(A级)、相同面板翘曲(板顶板底等效温度差-30℃)下不同车速的随机动荷载,车速为36、72和108 km/h时,考虑面板翘曲后的随机动荷载最小值相比于未考虑面板翘曲情况分别降低了3.35、3.57和3.19 kN,而随机动荷载最大值分别增大了4.37、3.90和5.33 kN,随机动荷载的标准偏差分别增加了0.16、0.37和0.41。也可以看到车速提高使面板翘曲对车辆随机动荷载的影响更加显著一些。
对比相同车速(72 km/h)、相同面板翘曲(-30℃)下不同等级路面的随机动荷载,路面等级为A、B、C和D时,随机动荷载的标准偏差分别增加了0.37、0.17、0.08和0.04。对比变化值发现,随着路面等级降低,面板翘曲对车辆随机动荷载的影响情况逐渐减弱。从图5(b)也可以看出,D级路面考虑面板翘曲前后的随机动荷载基本没有差别。值得注意的是,对于车速为72 km/h时,采用本文模型计算得到D级路面的随机动荷载的最小值已为负值,这说明了此时车辆车轮已经脱离路面,车路联接计算模型出现不适应。
下面借助功率谱密度进一步分析面板翘曲对车辆随机动荷载的影响。图7表明面板翘曲对随机动荷载功率谱密度在某些特定时间频率上值有影响,且随着车速增加或路面等级提高,影响情况越显著。这一点与面板翘曲对随机动荷载的影响与对路面不平度的影响情况基本一致。从图5可以看出,对于不同等级路面,其随机动荷载的功率谱密度均在频率为4 Hz,8 Hz,…,4n,…处存在波动,且波动现象随频率增加逐渐衰弱,其原因与不平度功率谱密度变化情况相同。随着路面等级降低,面板翘曲对随机动荷载功率谱密度影响减弱,对D级路面随机动荷载功率谱密度影响很小。
对比图7(a),(c),(d)可以发现,车速越大,面板翘曲对随机动荷载的影响越明显,且在基本频率值处的动荷载功率谱密度值变化最大。车速为36 km/h、72 km/h和108 km/h时,考虑面板翘曲使车辆随机动荷载的功率谱密度分别在2Hz、4Hz和6Hz处增大了9.59、40.82和61.86 kN2·s。

图7 面板翘曲对车-路耦合作用的随机动荷载的影响Fig.7 Effect of slab curling on dynamic load under coupling action between vehicle and road
总结来看,动荷载功率谱密度和不平度功率谱密度受面板翘曲的影响变化规律相同,与板长和车速有关,若车速为v,翘曲路面板长为L,面板翘曲对不平度功率谱密度和动荷载功率谱密度产生最显著影响对应于的频率为1/(L/v)。
3 面板翘曲量级的影响
实际路面在使用阶段由于早龄期固化翘曲和长期温度场的影响,面板翘曲量往往是不断变化的。以下将分别分析面板温度差为+10℃、0℃、-10℃、-20℃和-30℃的翘曲对路面不平整度和随机动荷载的影响。
3.1 对不平度和车辆随机动荷载的影响
表6给出了典型计算工况下数值模拟结果的性质。图8为不同面板翘曲对路面不平整度和车辆随机动荷载的模拟值的影响情况。
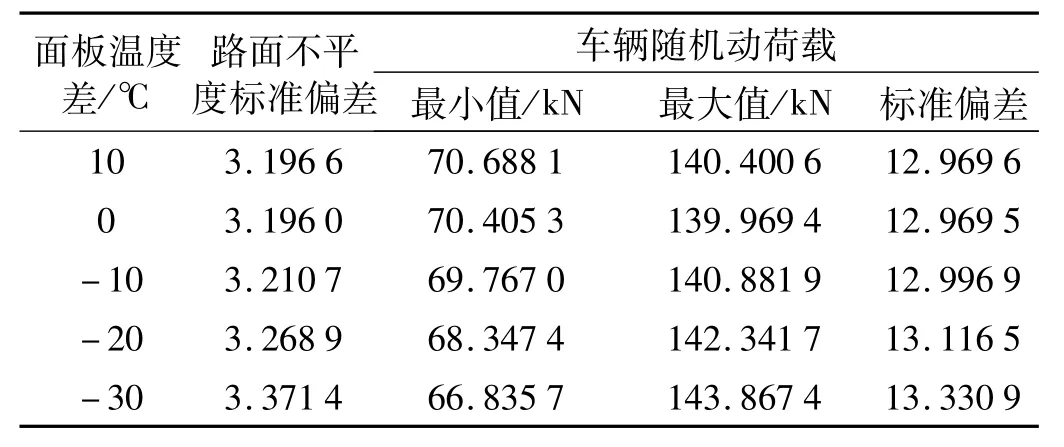
表6 面板翘曲量对路面不平度和车辆随机动荷载的影响Tab.6 Effect of slab curling on roughness and dynamic load

图8 面板翘曲对路面不平度和随机动荷载模拟结果的影响Fig.8 Effect of slab curling on roughness and dynamic load
分析发现面板向下翘曲对路面不平整度和车辆随机动荷载影响很小,从表6和图8可以看出,与面板没有翘曲(0℃)时相比,考虑面板翘曲为+10℃后路面不平度标准偏差、动荷载标准偏差、随机动荷载最小值和最大值均没有明显变化,差值分别为0.000 6、0.000 1、 0.282 8和0.431 2 kN。可以忽略。面板向上翘曲时,随着翘曲量的增大,路面不平度标准偏差和动荷载标准偏差逐渐增大,随机动荷载最小值呈变小趋势,最大值呈增大趋势,且各自变化幅度越来越明显。
图9和图10分别从功率谱密度的角度分析了不同面板翘曲量对路面不平整度和车辆随机动荷载的影响,图中路面等级为A级,车速为72 km/h。
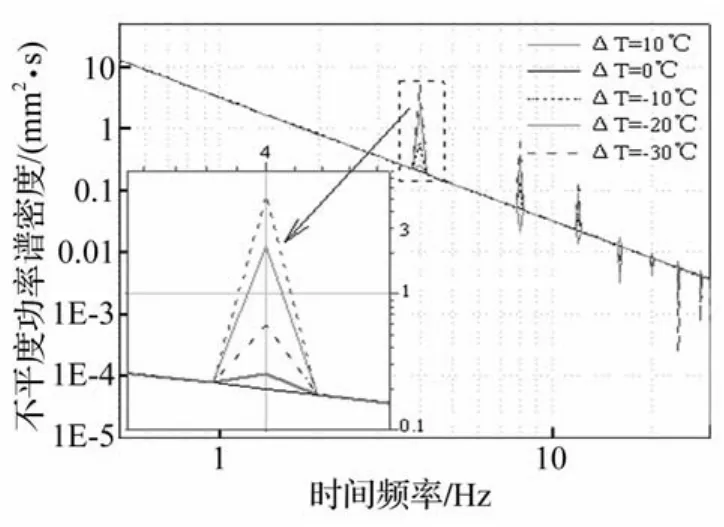
图9 面板翘曲大小对路面不平度功率谱密度的影响Fig.9 Effects of slab curling on power spectral density of roughness

图10 面板翘曲大小对车辆随机动荷功率谱密度的影响Fig.10 Effects of slab curling on power spectral density of dynamic load
从图可以看出,面板翘曲量级仅影响与板长和车速相关频率处的路面不平度功率谱密度和车辆随机动荷载功率谱密度,且翘曲量越大,其对路面不平整度和随机动荷载的影响越显著。
分析不同面板翘曲量对基本频率处(4Hz)路面不平度功率谱密度和车辆功率谱密度的影响(图9和图10)发现,面板翘曲越大,其对路面不平整度和随机动荷载的影响越明显。-30℃的面板翘曲对不平度和随机动荷载功率谱密度影响最显著,其次分别是-20℃、-10℃和+10℃,其中+10℃的面板翘曲对功率谱密度的影响明显小于-10℃面板翘曲的影响。据此可以看出,通过施工尽量调节面板处于较小的向上翘曲,或者尽量保持面板向下翘曲将有助于减小车辆的动荷载作用。
3.2 对行车舒适性的影响
路面不平整度是影响行车舒适性的最直接因素。对于行车舒适性问题,ISO 2631[15]采用人体加权加速度均方根值作为行驶舒适性基本评价指标,并给出加速度均方根值与人体舒适性的关系。下面将分析不同翘曲量级和不同车速下对行车舒适性的影响。假定乘客和车辆上部车厢部分的运动情况相同,计算模型默认参数见表7。

表7 行车舒适性计算默认参数Tab.7 Default parameters in calculating riding comfort
路面等级A图11为不同车辆参数、车速、面板翘曲下车辆上部(车厢部分)竖向加速度均方根值变化情况。可以看到,面板翘曲会影响路面的行车舒适性,面板翘曲越大,路面行车舒适性越差。同时也可以看到车辆参数均显著影响车辆上部竖向加速度均方根值,即影响行驶舒适性。轮胎刚度或悬挂系统刚度越大、或轴重越小、或路面等级越低、或车速越高,车辆上部竖向加速度均方根值越大,行车舒适性越差,而轮胎阻尼越大车辆上部竖向加速度均方根值越小,行车舒适性越好。车辆悬挂系统的阻尼比较特殊,存在一个最佳值使得行车舒适性最优。

图11 不同计算参数对车辆上部竖向加速度均方根值影响Fig.11 Effect of different parameters on root-mean-square value of vertical acceleration
对比图11中各参数的影响量级发现,路面等级、悬挂系统刚度和轴重对行车舒适性影响最显著,其他车辆参数次之,如轮胎刚度、悬挂系统刚度、车速等,面板翘曲和轮胎阻尼。虽然会影响行车舒适性,但是并不会使路面行车舒适性显著降低。
4 讨 论
(1)进一步深入分析可以发现,实际上面板翘曲属于影响路面板平整度多个尺度因素的其中之一。观察面板翘曲影响的基频值,发现由于沿路线行进方向尺度较大(一般我国路面板长5 m),基频值较低。观察对人的振动效应,人体胸腹系统固有频率为3~6 Hz,而头颈肩固有频率为20~30 Hz[12],因此从共振角度可以看到固化翘曲对人体胸腹系统的影响更显著。而显著影响头颈肩舒适性的不平整尺度将在更短的纵向范围。
我国目前普通公路水泥混凝土路面广泛采用三辊轴施工,观察路面板施工不平整度的实际形成情况可以发现,由于三辊轴施工的振动密实作用,特别是起振、转弯、停振部位将引起混凝土的密实不均,虽有抹面提浆,但仍然会在面板硬化后形成表面波浪。以对福建某公路水泥混凝土路面进行现场监测提取表面波浪如下:
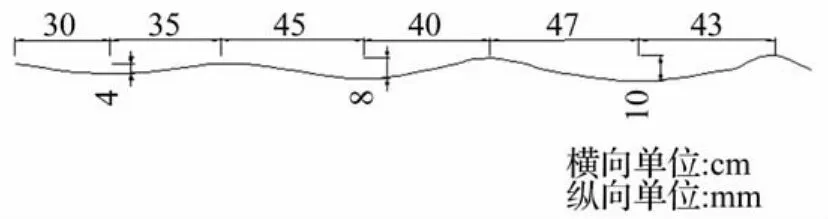
图12 某公路三辊轴施工引起的路面表面波浪Fig.12 Pavement surface wave caused by the construction of three roll shaft
从图12可以看到,三辊轴施工引起的面板不平整形状与固化翘曲的形状类似,但波距在60~90 cm之间,不平整波幅值更大(4~10 mm)。按照前述翘曲影响的分析方法和机制分析可以同理得到其影响特性,即这样的波浪由于幅值更大,其对车辆动荷载和舒适性的影响将比翘曲影响更为显著,特别是在车辆特定车速组合下,将显著影响主频与人体头颈肩敏感的20Hz~30Hz频率范围接近,进一步造成人体的不舒适。
对比以上可以看到,本文分析方法和机制分析结论可以类推分析类似弧形不平整问题,同时也说明提升较小尺度范围的路面平整度也是改善水泥混凝土行驶舒适性和耐久性的关键。
(2)固化翘曲的形成和量级受到施工时段、外部气候环境、混凝土材料性质和路面结构型式、约束水平等系列因素的影响,通过精细化的施工控制和材料设计,可以调节具体工程水泥混凝土路面固化翘曲的形成和量级。从图10和图13面板翘曲对随机动荷载和舒适性的影响曲线特征观察可以看到,板顶板底对应温度差为-10℃的翘曲是一个敏感界限,大于-10℃的向上翘曲影响敏感性将增强,因此可以建议在通过施工控制固化翘曲量级时,亦控制面板尽量处于正温度梯度下,或者负温度差小于-10℃。
(3)重型车辆是路面过早破坏的直接诱发原因,而车辆与路面之间本质是一个动力相互作用过程。固化翘曲影响车辆动荷载特征,进而可能影响路面损伤和疲劳的破坏机制,此间机制需结合面板的动力学相应和混凝土的材料本构进行综合分析,此间内容将另文发表。
5 结 论
(1)早龄期固化翘曲与服役阶段温度场共同作用下路面板会出现向上或向下的面板翘曲。面板向下翘曲对路面不平整度和车辆随机动荷载的影响很小,理论分析路面不平整度和车辆随机动荷载时,可以忽略面板向下翘曲的影响。面板向上翘曲时,随着翘曲量的增大,路面不平整度和随机动荷载的波动范围增大,离散性增加。同样量级的正温度差影响明显小于负的温度差。
(2)面板翘曲对较高等级平整路面的不平整度和随机动荷载影响较为显著,主要影响与板长和车速相关(n/(L/v)Hz)频率处的路面不平度和车辆随机动荷载参数值,而对于不平整粗糙的路面影响则不大。车速越高面板翘曲影响越显著。面板翘曲也会影响路面的行车舒适性,但小于路面等级、车辆参数、车速的影响。
(3)本文分析方法和机制分析结论可以类推分析类似弧形不平整问题。面板翘曲属于影响路面板平整度多个尺度因素的其中之一,由于沿路线行进方向尺度较大,其影响的敏感基频值较低。主要对人体胸腹系统影响显著,三辊轴施工引起的面板不平整形状与固化翘曲的形状类似,但波距在60~90cm之间,幅值更大。类推分析表明这样的波浪由于幅值更大,其对车辆动荷载和舒适性的影响将比翘曲影响更为显著,特别是在车辆特定车速组合下,影响频率范围在20~30 Hz之间,与人体头颈肩敏感频率接近。对比说明提升较小尺度范围的路面平整度也是改善水泥混凝土行驶舒适性和耐久性的关键。
(4)从面板翘曲对随机动荷载和舒适性的影响曲线特征观察可以看到,板顶板底对应温度差为-10℃的翘曲是一个敏感界限,大于-10℃的向上翘曲影响敏感性将增强,建议通过施工控制固化翘曲量级时,亦控制面板尽量处于正温度梯度下,或者负温度差小于-10℃。
[1]Byrum C R.Analysis by high-speed profile of jointed concrete pavement slab curvatures[J].In Transportation Research Record1730,TRB,NationalResearchCouncil,Washington,D.C.,2000:1-9.
[2]Eisenmann J,Leykauf G.Effect of paving temperatures on pavement performance[C].2nd International Workshop on the Design and Evaluation of Concrete Pavements,1990:419 -431.
[3]Hansen W,Wei Y,Smiley D L,et al.Effects of paving conditions on built-in curling and pavement performance[J].International Journal of Pavement Engineering,2006,7(4):291-296.
[4]Suprenant B A.Why slabs curl-part I[J].Concrete International,March,2002:56-61.
[5]Schindler A K,Terry D,McCullough B F.Temperature controlduringconstructiontoimprovethelongterm performance of portland cement concrete pavements[R].Center for Transportation Research,The University of Texas at Austin,May 2002.
[6]Hiller J E,Roesler J R.Determination of critical concrete pavement fatigue damage locations using influence lines[J].Journal of Transportation Engineering,ASCE,2005,131 (8):599-607.
[7]Shreenath R,Jeffery R S M,Roesler M.Characterizing effectivebuilt-incurlingfromconcretepavementfield measurements[J].Journal of Transportation Engineering,ASCE,2005,131(4):320-327.
[8]JTG D40-2011.公路水泥混凝土路面设计规范[S].北京:人民交通础版社2011.
[9]刘献栋,邓志党,高峰.基于逆变换的路面不平度仿真研究[J].中国公路学报,2005,18(1):122-126.
LIU Xian-dong,DENG Zhi-dang,GAO Feng.Study of simulation of road roughness based on inverse transform[J].China Journal of Highway and Transport,2005,18(1):122 -126.
[10]刘献栋,邓志党,高峰.公路路面不平度的数值模拟方法研究[J].北京航空航天大学学报,2003,29(9):843-846.
LIU Xian-dong,DENG Zhi-dang,GAO Feng.Research on the method of simulating road roughness numerically[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(9):843-846.
[11]Kim D,Salgado R,Altschaeffl A G.Effects of supersingle tire loadings on pavements[J].Journal of Transportation Engineering,2005,131(10):732-743.
[12]胡昌斌.冲击压路机破碎改建旧水泥混凝土路面技术[M].北京:人民交通出版社,2007.
[13]Hardy M S A,Cebon D.Response of continuous pavements to movingdynamicload[J].JournalofEngineering Mechanics,1993,119(9):1762-1780.
[14]Sun L,Deng X J.Predicting vertical dynamic loads caused by vehicle-pavement interaction[J].Journal of Transportation Engineering,1998,124:470-478.
[15]ISO 2631.Guide for the evaluation of human exposure to Whole-body Vibrations[S].
Effects of a slab's built-in curling on dynamic load and riding comfort of vehicles
HU Chang-bin,SUN Zeng-hua
(College of Civil Engineering,Fuzhou University,Fuzhou 350108,China)
Concrete pavement slab may get a significant built-in curling due to dry shrinkage and built-in temperature gradient at its initial stage.Here,effects of built-in curling of the slab on dynamic load and riding comfort of vehicles were analyzed based on a quarter vehicle vibration model and the road-vehicle dynamic interaction analysis method.The results showed that the built-in curling has more effects on roughness and random dynamic load of a highergrade pavement,it mainly affects road roughness and vehicle random dynamic load parameters related to frequency of (slab length/speed);built-in curling and environmental temperature gradient produce upward or downward curling,slab upward curling has a larger influence on pavement roughness and random dynamic load,but down warping has little effect;riding comfort,pavement grade,vehicle parameters and vehicle speed have more significant effects on riding comfort than built-curling does.Three-roll shaft construction's built-in curling shape has a stronger effect than asiab's built in curling does;effective built-in temperature difference keeping below-10℃may lead to a good performance of pavement slab.
cement concrete pavements;built-in curling;roughness;dynamic load;riding comfort
U416
A
10.13465/j.cnki.jvs.2014.23.001
国家自然科学基金项目(50908056,51478122)
2013-06-07 修改稿收到日期:2014-01-09
胡昌斌男,教授,博士,1974年生
