动态增殖流形学习算法在机械故障诊断中的应用
2014-05-16汤宝平
宋 涛,汤宝平,邓 蕾
(重庆大学机械传动国家重点实验室,重庆 400044)
动态增殖流形学习算法在机械故障诊断中的应用
宋 涛,汤宝平,邓 蕾
(重庆大学机械传动国家重点实验室,重庆 400044)
针对现有的批量式流形学习算法无法利用已学习的流形结构实现新增样本的快速约简的缺点,提出增殖正交邻域保持嵌入(Incremental Orthogonal Neighborhood Preserving Embedding,IONPE)流形学习算法。该算法在正交邻域保持嵌入算法基础上利用分块处理思想实现新增样本子集的动态约简。从原始样本中选取部分重叠点合并至新增样本,对重叠点和新增样本子集不依赖原始样本使用正交邻域保持嵌入(ONPE)进行独立约简获取低维嵌入坐标子集,并基于重叠点坐标差值最小化原则,将新增样本低维嵌入坐标通过旋转平移缩放整合到原样本子集中。齿轮箱故障诊断案例证实了IONPE算法具有良好的增量学习能力,在继承ONPE优良聚类特性的同时有效提高了新增样本约简效率。
增殖流形学习;正交邻域保持嵌入;动态约简;分块处理;故障诊断
流形学习以其良好的非线性维数约简能力成功应用于机械故障诊断领域[1-2]。但是机械设备故障诊断更多时候需要长期在线监测,样本数据会不断的动态增加。而现有流形学习算法大多采用批处理模式,即一次性获取全部样本进行约简。每新增一个样本时,需要将新增样本合并到原有的样本中,全部样本重新进行流形学习以实现维数约简,而无法利用原有样本的训练结果。随着样本数量的增大,运算复杂度将迅速提高,耗时过长,不具备动态数据处理能力。由于这一缺陷,增量流形学习成为了流形学习一个重要研究方向[3-5]。增量流形学习算法利用已经学习过的样本的低维流形结构处理新增样本,避免已训练样本的重复学习,从而提高新增样本处理效率。然而,增量流形学习算法每次只能处理一个新增样本[6-7],多个样本逐点更新计算代价依然很高,难以满足大量新增数据动态处理需求。
增殖学习是利用分块处理方法将大的数据集分为各个小的数据子集,分别约简后再进行整合,该思想无需逐点处理新增样本,能提高大量样本动态添加处理效率。如曾宪华等提出一种动态增殖LLE算法[8],但该算法要求数据子集必须是相邻或重叠的,否则,低维流形会出现较大扭曲或是无法整合,限制了该算法的实际应用。本文构建一种增殖正交邻域保持嵌入算法(Incremental Orthogonal Neighborhood Preserving Embedding,IONPE)。对于新增样本子集,从原有样本集中提取各类数据中心点合并至新增样本子集,使得两个样本集存在重叠点,再对重叠点和新增样本子集采用ONPE进行约简,基于重叠点在两个样本集中的低维嵌入坐标差值最小化原则对新增样本低维嵌入流形进行旋转平移缩放变换,将新增样本整合到原有样本子集中。重叠点的存在能避免增殖LLE所述问题,从而实现新增样本集的快速有效降维。
1 增殖正交邻域保持嵌入算法
正交邻域保持嵌入是基于近邻关系保持嵌入改进的一种正交化降维方法[9],通过迭代计算正交基函数得到数据的低维嵌入坐标,在降维过程中保持数据点的局部几何信息。
1.1 正交邻域保持嵌入
设原始高维样本集为X={x1,x2,…,xn}∈RD,其中样本数为n,特征维数为D,,降维后的特征集为Y={y1,y2,…,yn}∈Rd,即降维后的维数为d,其中d<D,则Y=ATX,其中A∈RD×d,为变换矩阵。ONPE算法求解过程分为如下三步:
(1)非奇异处理。在不损失任何信息的条件下将数据点xi投影到PCA子空间,并丢弃对应于特征值0的成分,使得矩阵XXT为非奇异,方便后续处理,设PCA投影矩阵为APCA。
(2)构建邻接图。对X中任一节点xi,找出距离最近的k个邻域节点xj,从xi到xj连一条有向的边,设权值为Wij,每个节点xi可通过它的k个最近邻线性重构,Wij反映了其近邻点对xi的重构贡献。
(3)计算ONPE正交投影向量。基于上述求解的权值矩阵W,构建低维嵌入坐标的重构误差函数,通过迭代求取求解正交投影向量为AONPE,则ONPE变换矩阵为A=APCAAONPE。
1.2 增殖正交邻域保持嵌入
ONPE算法具有良好的聚类特性,适用于模式识别的前端处理。但每新增一个样本时,需要对所有样本重新进行非奇异处理、构建邻接图并计算正交投影向量,存在大量的重复运算,算法复杂度高,不适用于动态样本集添加。增殖正交邻域保持嵌入对于新增样本子集,可不依赖原始样本,采用ONPE进行独立降维,再将降维后的低维数据集进行适当的平移旋转缩放变换,整合到原始样本集中,算法具体过程如下:
1.2.1 重叠点选取
为了使新增子集降维后的流形与原样本集有效的整合,本文从原样本集中选取部分样本点合并至新增样本集,使两个样本子集存在重叠点,基于重叠点在两个样本集中的低维嵌入坐标差值最小化原则对新增样本低维嵌入流形进行整合变换。重叠点的选取遵循两个原则:
(1)重叠点个数g大于低维流形维数d,保证后续平移旋转缩放变换有全局最优解;
(2)重叠点覆盖原有样本集低维嵌入流形各个区域,避免出现扭曲。
假设原样本集包含s种数据类别,本文从这s种数据中分别选取p个中心点作为重叠点,

式中(d+1)/s取整,每类数据的中心点的计算方法:

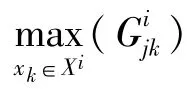


1.3 复杂度分析
ONPE的计算复杂度主要是由构建邻域图和计算正交变换矩阵决定。设原始样本个数为m,新增样本个数为n。对于批量处理方式,需处理样本个数为n1=n+m,构建邻域图的时间复杂度为O(n1logn1)[10],计算ONPE正交变换矩阵需要求解n1×n1矩阵的特征值和特征向量,时间复杂度为O),总体时间复杂度为T1=O(n1logn1+)。本文的增殖ONPE算法的计算主要包含n2=m+g个样本的ONPE降维和增殖变换。增殖变换涉及到(d+1)×g维矩阵广义逆求解,时间复杂度约为O[(d+1)3+g3],增殖变换总体时间复杂度为T2=O[n2logn2++(d+1)3+g3],由于n2,g,d ≪n1,所以一般情况下T2≪T1,即增殖算法的运算效率远远高于批量算法。
2 基于增殖ONPE的机械设备故障诊断流程
在机械设备状态监测过程中,增殖ONPE能快速地对新增样本集进行降维处理,进而进行模式识别,判断机械设备运行状态。其流程如图1所示。该诊断流程包括如下几个步骤:
(1)收集机械设备不同状态的多组振动信号数据,作为原始训练样本,使用时频域分析提取其高维特征,并使用ONPE流形降维方法进行降维获取原始样本低维嵌入坐标,并保存高维特征子集。
(2)设备状态监测过程中提取多组测试信号数据,通过分析取获取测试样本的高维特征子集,并依据上述重叠点选取方法从原始样本高维特征子集中选取部分样本并入新增样本子集。
(3)对新增样本子集和重叠点使用ONPE进行维数约简,获取新增样本低维嵌入坐标子集。使用增殖ONPE变换将新增样本低维嵌入坐标子集整合到原始样本中,得到所有样本低维嵌入坐标全集。
(4)使用K近邻分类器对新增样本进行模式识别,判断机械设备当前状态。
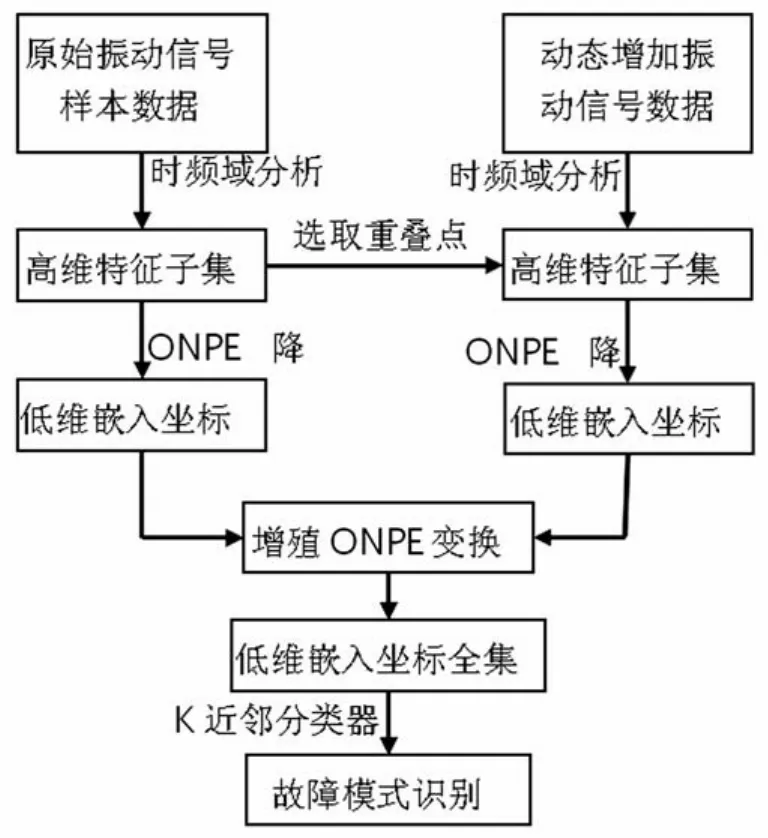
图1 基于增殖ONPE的机械设备故障诊断流程图Fig.1 The fault diagnostic process of machinery equipment based on IONPE
3 齿轮箱故障诊断案例
3.1 应用对象
应用美国预测与健康管理协会提供的齿轮箱故障振动数据并使用本文增殖ONPE算法进行故障诊断测试。该测试中所用齿轮箱结构如图2所示。

图2 齿轮箱结构图Fig.2 The structure of gearbox
齿轮箱由输入端至输出端经过两级减速,在齿轮箱输入轴和输出轴分别安装一个振动加速度传感器同步采集振动加速度信号,型号为Endevco(10mv/g),同时安装一个转速计采集转速信号,10脉冲/转。三个传感器的采样频率均为66,666.67 Hz(200 kHz/3)。实验在不同转速和不同负载工况下进行,输入轴转速包括1 800 r/min、2 100 r/min、2 400 r/min、2 700 r/min、3 000 r/min五种工况,每种转速下又分为高负载和低负载有种工况,每种工况下分别有8种不同的故障或正常状态。
3.2 齿轮箱故障诊断
本文选用转速3 000 r/min、低负载下齿轮箱输出轴端的振动信号进行故障诊断测试,取6种不同的齿轮箱故障状态振动信号数据,每种故障状态可能是单一故障或者复合故障,齿轮箱不同的故障对应的各个零部件状态如表1所示。其中32 T、96 T、48 T、80 T分别对应输入轴齿轮、中间轴齿轮1、中间轴齿轮2、输出轴齿轮,IS、ID、OS分别指输入轴、中间轴、输出轴。

表1 齿轮箱故障状态Tab.1 The fault status of gearbox
上述6种齿轮箱故障状态对应的振动信号时域波形如图3所示。每种状态分别取30组数据作为原始训练样本,样本长度为4 096点,每组数据分别提取时域标准差、有效值、峰值、偏度值、峭度值,频域幅值均值、幅值方差、幅值偏度、幅值峭度、幅值一阶中心距、幅值二阶中心距作为高维特征向量。另外每种状态分别取30组数据作测试样本,提取上述时频域特征值作为高维特征向量,并使用本文的增殖ONPE算法对测试样本进行降维,最后使用KNNC进行模式上识别。为验证本文方法的有效性,本文同时采用批量ONPE算法和增殖LLE算法作约简进行对比测试。ONPE约简方法中构建邻域图的近邻参数均设置为K=12,为使降维结果可视化,低维嵌入维数均设置为d=3。IONPE算法中由于数据类别为6种,故每类只需选取1个中心点,即重叠点个数g=6。三种方法的低维嵌入坐标如图4所示。降维后进行模式识别的准确率以及降维过程耗时如表2所示。
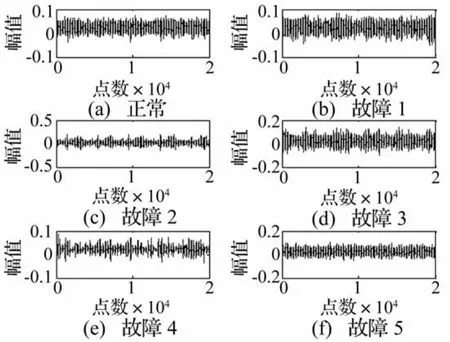
图3 齿轮箱不同故障振动信号Fig.3 The vibration signals of different gearbox faults

图4 不同降维方法低维嵌入坐标Fig.4 The low-dimensional embedding coordinates with different dimension reduction methods

表2 不同约简方法的故障识别率及耗时Tab.2 The fault diagnosis accuracy and time-consuming of different reduction methods
由图4(a)和图4(b)可以看出,增殖ONPE算法和批量ONPE算法都能将齿轮箱各种状态数据能明显分离开来,充分发挥了ONPE算法优良的聚类特性,使相同类别的样本在空间分布上聚集在一起。而增殖LLE算法虽然训练样本和测试样本对应的各种状态数据分别能够分离开来,但是测试样本约简后的结果不能很好的融合到训练样本中,在空间分布上出现脱离现象,原始样本和测试样本相同状态的数据不能聚集在一起。而本文增殖ONPE算法选取各类数据的中心点作为重叠点并入测试样本中,基于重叠点在训练样本和测试样本的差值最小化原则将测试样本低维嵌入整合到训练样本低维空间中,能有效处理新增样本。使相同类别的样本在空间中分布在相同的位置,其约简效果与批量ONPE算法类似。
表2所示不同约简方法的状态识别率也证实了本文增殖ONPE方法降维效果与批量ONPE降维效果相当,模式识别的总体识别率均达到95%以上。从新增样本的维数约简时间来看,增殖LLE算法的耗时最短,但其识别率只有67.22%,远低于另外两种方法,难以满足故障模式识别需求。本文方法对180个新增样本约简耗时仅为为0.172 6 s,是批量处理方式的38.4%(约简耗时是在windows7操作系统、core i3(2.10 GHz)、4G内存环境下测试所得),大大提高新增样本的处理速度,更加适用于机械设备状态监测过程中的动态模式识别。
3.3 算法聚类度分析
聚类特性是流形学习一个重要性能,在维数约简过程中保持近邻关系,使同类样本聚集,不同类样本分开,有利于模式识别。由于增殖ONPE算法采用分块、整合策略进行维数约简,有可能对样本聚类度产生影响,这里将进一步分析增殖ONPE算法的聚类特性随新增样本子集个数的变化关系。定义聚类度表达式为:

同样以上述数据进行聚类度分析测试,齿轮箱6种状态分别取30组数据作为训练样本,其余180组数据作为测试样本,每次添加10组测试样本进行增量学习,并计算其聚类度。同时采用批量ONPE进行对比,聚类度随新增样本点数变化关系如图5所示。

图5 新增样本点数与聚类度关系Fig.5 The relation between the number of additional samples and the clustering degree
由图5可以看出增殖ONPE算法聚类度随着新增样本数量的增加呈现一定的波动,但总体上没有明显增长趋势,且增量ONPE算法的聚类度与批量式算法结果基本一致,维持了ONPE算法良好的聚类效果。
4 结 论
增殖ONPE流形学习算法将批量处理模式转化为分块处理模式对新增样本进行约简,通过选取重叠点,并基于重叠点在原始样本和新增样本子集中的低维坐标差值最小原则,将新增样本进行旋转平移缩放变换整合到原始样本子集中。增殖ONPE算法很大程度上降低了维数约简的运算复杂度,提高新增样本的处理效率,并且维持了ONPE算法良好的聚类特性。齿轮箱振动故障数据的故障识别结果表明增殖ONPE算法具有良好动态增殖学习能力,适用于机械设备在线状态监测。
[1]Li F,Tang B P,Yang R S.Rotating machine fault diagnosis using dimension reduction with linear local tangent space alignment[J].Measurement,2013,46:2525-2539.
[2]Jiang Q S,Jia M P,Hu J Z,et al.Machinery fault diagnosis using supervised manifold learning[J].Mechanical Systems and Signal Processing,2009,23:2301-2311.
[3]Kouropteva O,Okun O,Pietikanen M.Incremental locally linear embedding[J].Pattern Recognition,2005,38:1764-1767.[4]Liu X M,Yin J W,Feng Z L et al.Incremental manifold learning via tangent space alignment[C]//Proceedings of the Second International Conference on Artificial Neural Networks in Pattern Recognition.Ulm,Germany,2006:107-121.
[5]Law M H C,Jain A K.Incremental nonlinear dimensionality reduction by manifold learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(3):337-391.
[6]杨庆,陈桂明,童兴民,等.增量式局部切空间排列算法在滚动轴承故障诊断中的应用[J].机械工程学报,2012,48 (5):81-86.
YANG Qing,CHEN Gui-ming,TONG Xing-min,et al.Application of incremental local tangent space alignment algorithm to rolling bearings fault diagnosis[J].Journal of Mechanical Engineering,2012,48(5):81-86.
[7]张熠卓,徐光华,梁霖,等.利用增量式非线性流形学习的状态监测方法[J].西安交通大学学报,2011,45(1):64 -69.
ZHANG Yi-zhuo,XU Guang-hua,LIANG Lin,et al.Condition monitoring method for mechanical equipments based on incremental nonlinear manifold learning[J].Journal of Xi'an Jiaotong University,2011,45(1):64-69.
[8]曾宪华,罗四维.动态增殖流形学习算法[J].计算机研究与发展,44(9),2007:1462-1468.
ZENG Xian-hua,LUO Si-wei.A dynamically incremental manifold learningalgorithm[J].JournalofComputer Research and Development,2007,44(9):1462-1468.
[9]刘小明.数据降维及分类中的流形学习研究[D].杭州:浙江大学,2007.
[10]Saul L,Roweis S.Think globally1 Fit locally:Unsupervised learning of low dimensional manifolds[J].Journal of Machine Learning Research,2002,4:119-155.
A dynamic incremental manifold learning algorithm and its application in fault diagnosis of machineries
SONG Tao,TANG Bao-ping,DENG Lei
(The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400044,China)
The current batch manifold learning algorithms can't achieve rapid dimension reduction of additional samples with learned manifold structures.Here,the incremental orthogonal neighborhood preserving embedding(IONPE)manifold learning algorithm was proposed.With it,dynamic incremental learning for additional samples was realized with a block processing idea based on orthogonal neighborhood preserving embedding.Firstly,some overlapping points were selected from the original samples and added to the additional samples.Secondly,the subset of low-dimensional embedding coordinates of additional samples was obtained with ONPE independing on the original samples.Finally,based on the principle of minimizing the differences of the overlapping point coordinates,the low-dimensional embedding coordinates of the additional samples were integrated into the original samples with rotating,shifting and scaling transformations.The fault diagnosis case of a gearbox confirmed that the IONPE algorithm has a good incremental learning ability,it improves the processing efficiency of the additional samples while inheriting the superior clustering performance of ONPE.
incremental manifold learning;ONPE;dynamic reduction;block processing;fault diagnosis
TH165.3
A
10.13465/j.cnki.jvs.2014.23.003
国家自然科学基金(51275546);高校博士点专项科研基金(20130191130001)
2013-08-01 修改稿收到日期:2013-12-12
宋涛男,博士生,1987年7月生
汤宝平男,博士,教授,1971年9月生
邮箱:bptang@cqu.edu.cn
