钢-玄武岩纤维复合筋混凝土框架结构非线性地震反应分析
2014-05-16肖同亮邱洪兴陈春超
肖同亮,邱洪兴,陶 欣,孙 建,陈春超
(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
钢-玄武岩纤维复合筋混凝土框架结构非线性地震反应分析
肖同亮,邱洪兴,陶 欣,孙 建,陈春超
(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
钢-纤维复合筋是一种耐腐蚀、具有稳定二次刚度等特性的新型结构材料。开展了钢-玄武岩纤维复合筋混凝土框架结构的非线性地震反应研究工作,由复合筋的应力-应变本构关系出发,利用修正Gauss-Radau积分法推导了杆件单元柔度矩阵,并用于框架结构非线性时程响应分析。参考现行规范设计了一个8度区的普通钢筋混凝土多层框架结构和一个对比钢-玄武岩纤维复合筋混凝土框架结构,比较了两个结构在相同地震输入下结构自振周期变化率、非线性时程响应和杆端出铰时间和位置等抗震性能指标。结果表明:在多遇和罕遇地震动输入下,配置钢-玄武岩纤维复合筋混凝土框架结构的最大弹塑性位移与层间转角等指标比普通钢筋的框架结构有所减小;在罕遇水准的地面运动输入下结构自振周期变化率小于RC框架结构,结构刚度退化和损伤程度更小;杆端出铰时间相对更晚、数量更少且更易形成梁铰塑性耗能机制。钢-玄武岩纤维复合筋可充分利用材料的强度,通过合理配置钢筋与玄武岩纤维的比例能够有效控制框架结构的塑性变形、减小结构残余位移,从而减小重力二阶效应对柱的不利影响,改善结构在大震下的性能,确保大震不倒的安全性能目标。
钢-玄武岩纤维复合筋;混凝土框架结构;时程分析;二次刚度;非线性响应
普通钢筋混凝土应用于水工、海港、化工等恶劣环境时的钢筋锈蚀问题非常严重,而纤维塑料(Fiber Reinforced Polymer,简称FRP)筋与普通钢筋相比具有抗腐蚀性能好、抗拉强度高等特点。采用FRP筋取代钢筋用于混凝土结构是解决钢筋锈蚀的有效方法之一,但FRP筋为脆性材料且弹性模量低,单独使用时其混凝土结构往往存在刚度低、使用阶段结构挠度大和易发生脆性破坏等缺点,限制了其在工程中的应用。
结合普通钢筋弹性模量高、延性好和FRP耐腐蚀性能强、极限强度高的优点,吴智深等[1]提出并工业化生产制作了以钢筋为内芯,外包纵向连续纤维的钢-纤维复合筋(Steel Fiber Composite Bar,简称SFCB),如图1所示。复合筋在力学性能上综合了FRP和钢筋的优点:初始阶段有较高弹模;钢筋屈服后FRP继续发挥作用,有一定的二次刚度;FRP断裂后,钢筋继续发挥作用,可保证复合筋具有良好的延性。

图1 SFCB产品示意图Fig.1 SFCB product schematic diagram
近几年,课题组在SFCB材料基本力学性能和构件试验方面展开大量研究。结合单调拉伸和往复拉伸试验,通过复合法则给出了SFCB在往复荷载下的应力应变关系,提出了理论计算模型[2],如图2所示;孙泽阳等[3]对4个轴压比为0.12的SFCB增强混凝土柱和1 个RC对比柱开展了低周反复荷载试验研究,结果表明SFCB增强混凝土柱有稳定的二次刚度,在复合筋内芯钢筋屈服后,SFCB增强混凝土柱承载力仍可稳定提高。

图2 SFCB与普通钢筋循环加载下试验曲线对比Fig.2 Test curves of SFCB and ordinary steel under the cyclic loading
钢筋混凝土框架是钢筋混凝土结构中应用最为广泛的结构体系之一,结构的弹塑性建模方法与地震反应分析是结构抗震领域的重要研究内容。其内容牵涉到钢筋和混凝土的本构关系及其相互作用模拟、结构计算理论、数值算法实现等各方面的问题。在弹塑性建模方面,最为关键的核心问题是钢筋混凝土恢复力模型与计算单元的选取。早期常用的框架结构整体分析模型主要有层间模型和基于构件的平面杆系模型;近十年,基于纤维单元的有限元方法发展迅速,成为目前解决钢筋混凝土框架非线性分析问题的主要方法之一[4]。
将钢-玄武岩纤维复合筋用于混凝土框架结构不仅使结构具有良好的耐久性,对结构抗震性能的影响也具有重要的研究意义。本文开展了钢-玄武岩纤维复合筋混凝土框架结构的非线性地震反应研究工作,从材料非线性出发,根据复合筋的应力-应变关系,利用修正Gauss-Radau积分法推导了杆件单元柔度矩阵,并用于多层框架结构非线性时程响应计算,比较了结构计算模型在地震波输入下的非线性响应和抗震性能。
1 材料本构关系与计算模型
1.1 复合筋的应力应变关系
以钢筋屈服作为复合筋的屈服点,以纤维拉断作为极限状态,假设复合筋纤维外包覆层与内芯钢筋之间的截面结合良好,在承受荷载的过程中,两者变形协调,运用复合叠加原则得到复合筋的应力-应变关系[1]:
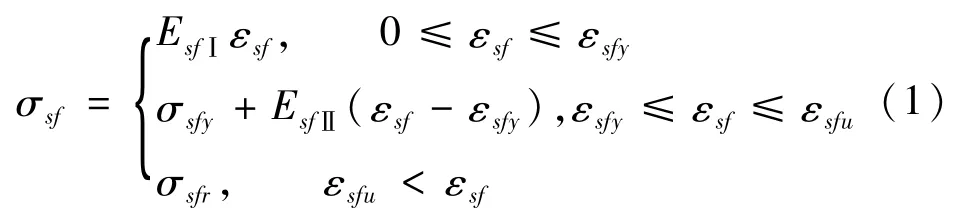
式中EsfⅠ=(EsAs+EfAf)/A,EsfⅡ=EfAf/A;σsfr=fyAs/A;EsfⅠ为复合筋屈服前弹性模量,EsfⅡ为复合筋的屈服后弹性模量,σsf和εsf分别为复合筋应力和应变;σsfy和εsfy为复合筋的屈服应力和屈服应变;σsfu和εsfu为复合筋纤维断裂时的极限应力和极限应变,fsfr为复合筋的残余强度。
本文选用型号为4800tex的玄武岩纤维(BFRP),每束纤维面积为1.67 mm2。复合筋设计与计算使用的材料力学性能如表1所示。

表1 钢筋与玄武岩纤维的基本力学性能Tab.1 Basic mechanical properties of steel bar and basalt fiber
钢筋本构关系采用考虑等向应变硬化影响的两线型Menegotto-Pinto[5]滞回模型,该模型在计算上效率较高且与钢筋往复加载试验结果吻合良好,可反映包辛格效应。
为了便于对复合筋的材性与普通钢筋作比较,定义复合筋材性二次刚度比为
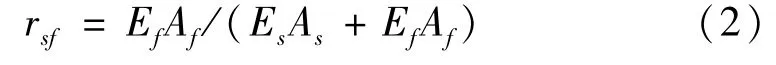
式中Es、As、Ef、Af分别为钢筋、纤维的弹性模量和截面积。复合筋材性的滞回模型类似于钢筋材料,可选取双线性随动强化模型,如图3所示。
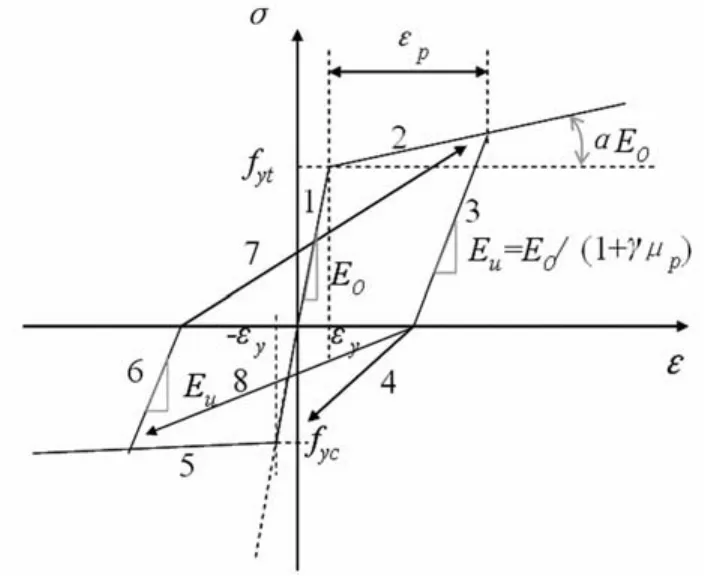
图3 复合筋应力-应变恢复力模型Fig.3 Stress-strain restoring force model of composite bar
1.2 混凝土材料的非线性
本文采用包含抗拉段的Kent-Scott-Park[6]混凝土应力-应变模型,混凝土模型在反复拉压下的滞回曲线如图4所示。

图4 混凝土反复荷载下滞回曲线Fig.4 Hysteretic behavior of concrete under cyclic loading
2 杆件单元模型
结构计算单元的选取是影响非线性地震反应的重要因素。杆系模型既能考察结构整体的地震反应又能较细致的考察构件层次的地震响应,本文采用杆端分布塑性铰单元模型分析框架结构的梁柱构件。该单元由单元两端的塑性铰区和中间的线弹性部分组成。单元的塑性集中发生在塑性铰区,如图5所示。
塑性区截面的力-变形关系可通过弯矩曲率关系表示,也可采用纤维截面通过材料的本构求得。本文杆端塑性区采用基于柔度法的纤维截面模型。纤维截面模型首先将截面离散为较小面积的纤维,通过赋予纤维不同材料应力-应变关系模型来考虑组合截面的力学性能。通过平截面假定建立构件截面的弯矩-曲率、轴力-轴向变形等关系。
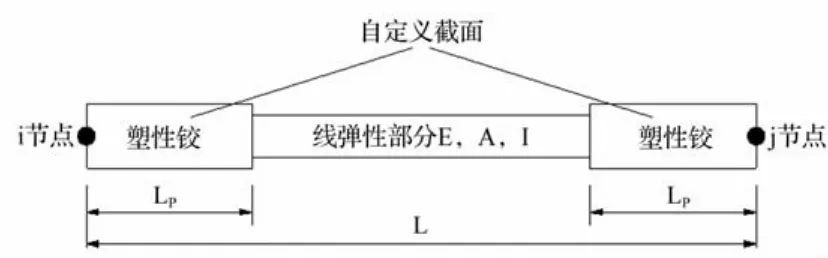
图5 杆端分布塑性铰单元模型Fig.5 Rod end distribution model of the plastic hinge element
纤维截面的截面刚度矩阵如式(3)所示。

基于柔度法的塑性铰杆单元中部积分采用弹性本构,不需要求解切线刚度与截面抗力,提高了求解速度。塑性铰单元柔度矩阵求解为

本文采用修正Gauss-Radau四点积分方法[7],取两端塑性铰两个端截面和弹性区段的两个积分点沿杆长积分,将三个部分的柔度叠加得到整个构件的柔度。

3 算 例
算例按照8度0.2g区,Ⅱ类场地第一设计分组进行抗震设计[8],抗震等级为二级,抗震设防类别为丙类。为了便于对比钢-玄武岩纤维复合筋混凝土框架结构和普通钢筋混凝土框架结构在抗震性能上的差异,采用OpenSEES数值模拟软件建立了2个六层三跨计算模型,其跨度、层高、总高度及梁柱截面尺寸均相同,但梁柱截面配筋不同,结构平面布置如图6所示。其计算参数是:框架梁、柱、楼板均现浇,混凝土强度等级为C30;梁截面为300 mm×600 mm,柱截面为500 mm×500 mm,板厚取100mm;结构的楼面恒载为4.0 kN/m2,活荷载为3.5 kN/m2;屋面恒载为6.0 kN/m2,活荷载为2.0 kN/m2,不考虑填充墙的作用。由于平面布置规则,取中间一榀横向框架进行分析计算,普通钢筋混凝土框架结构(以下称模型1)配筋如图7所示,钢-玄武岩纤维复合筋混凝土框架结构(以下称模型2)在模型1所配钢筋基础上按复合筋二次刚度比rsf配置,本文梁复合筋纵筋二次刚度比取0.2,柱复合筋纵筋二次刚度比取0.3。
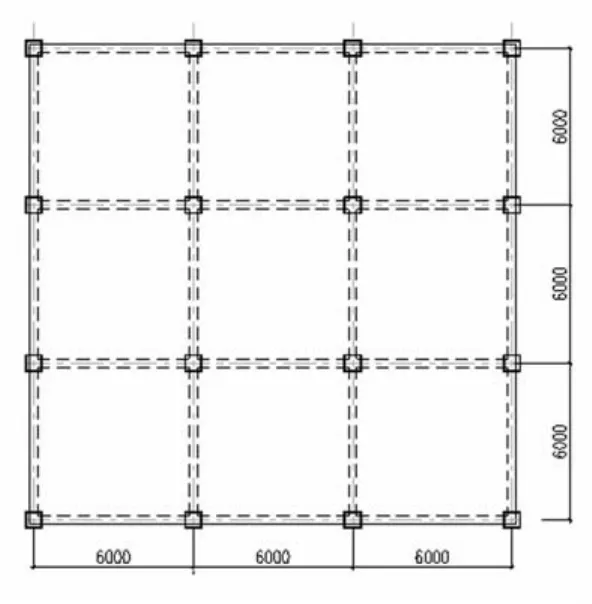
图6 结构平面布置图Fig.6 Structure layout

图7 框架结构尺寸与配筋图Fig.7 Frame structure size and reinforcement drawing
3.1 计算模型假定
为了简化结构计算,对框架结构计算模型[9]作如下假定:
(1)杆件横截面满足平截面假定,杆件变形以受弯和拉压变形为主,不考虑剪切变形和筋材与混凝土间的滑移。
(2)节点为刚性,不考虑节点的有限尺寸的影响;不考虑楼板翼缘对框架梁强度和刚度的贡献,即按矩形截面梁进行计算。
(3)基础假定为刚性,不考虑基础变形和沉降等因素对框架结构受力的影响;假定结构各楼层质量均匀分布于各楼板上。
结构阻尼模型采用瑞雷阻尼,阻尼系数按结构一二阶振型阻尼比为0.05确定;重力荷载采用等效均布荷载的形式施加于梁上并在进行动力分析前以静力荷载的形式先行施加,动力计算采用Newmark法逐步积分方案按地震波输入序列考虑前一时刻地震输入对后一时刻地震反应所造成的影响。
3.2 地震波的选取
本文选择1940年在美国记录的著名地震波EL Centro波(N-S方向)并对其峰值调整,多遇地震加速度峰值调整为70 cm/s2,罕遇地震加速度峰值调整为400 cm/s2。
4 分析结果与讨论
对于结构的非线性地震反应的评价,通常选用结构前几阶自振周期或频率、顶点位移、层间位移角、塑性铰分布与转动能力等指标来衡量。下面将给出配置复合筋与普通钢筋的框架结构非线性地震反应分析结果与各项指标比较。
4.1 自振周期比较
文献[10]采用损伤前后“自振频率变化平方比”来评估结构损伤程度,从物理意义上看,损伤前后结构的自振周期变化能够反映结构整体刚度的下降,即震后结构自振周期越大,结构损伤程度越严重,刚度退化也较明显。
在多遇地震输入下,结构基本处于弹性阶段,非线性发展尚不明显,结构震前震后的自振周期见表2。RC框架结构与复合筋框架结构自振周期震前震后变化不大。结构损伤程度较小,故自振周期变化率区别不明显。
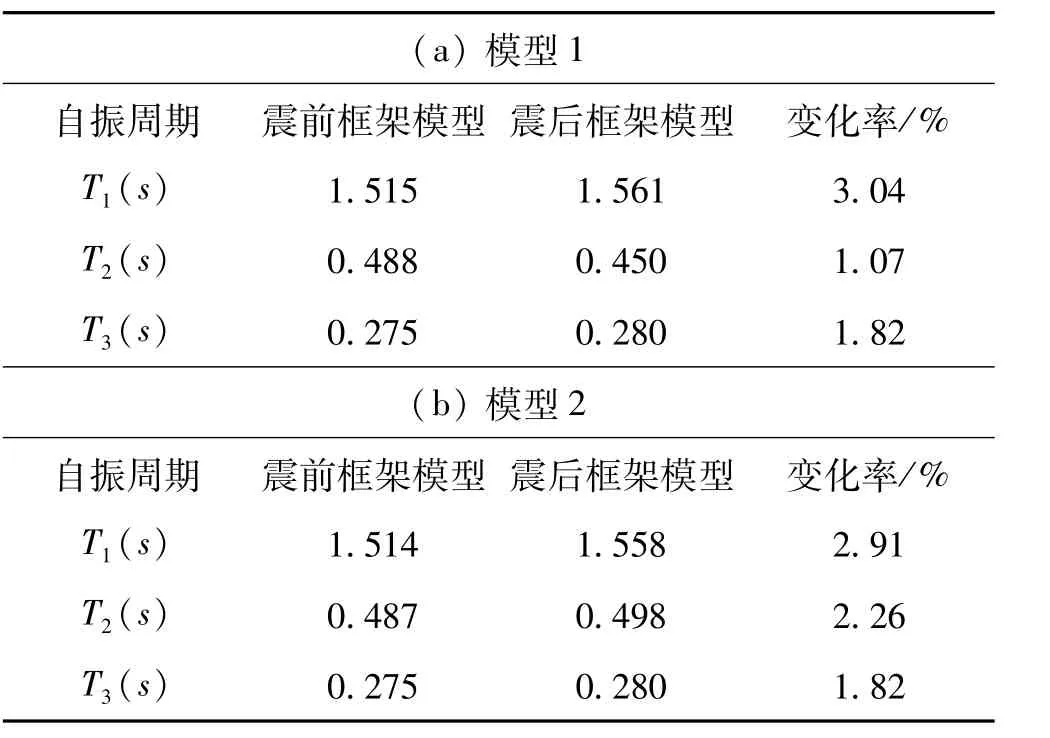
表2 多遇地震前后结构自振周期对比Tab.2 Comparison of pre-and post natural vibration period under the frequent earthquake
在罕遇地震下,结构进入弹塑性阶段,塑性变形显著,结构损伤程度严重,震前与震后结构自振周期变化较为显著,见表3。

表3 罕遇地震前后结构自振周期对比Tab.3 Comparison of pre-and post natural vibration period under the the rare earthquake
表2和表3震前与震后的自振周期变化率一定程度上反映了结构损伤的程度。结构进入弹塑性阶段后,构件由于混凝土开裂、筋材屈服等使构件刚度下降,导致自振周期增加。从模型1和模型2震前震后的变化率来看,模型2受损伤程度和整体刚度退化要小于模型1。
4.2 结构时程响应比较
多遇地震下框架结构模型时程响应塑性发展程度不明显,残余位移较小,在此不再赘述。表4给出了2个框架结构算例在罕遇地震下的顶点位移和层间位移角的最大值。

表4 罕遇地震下框架结构位移时程响应比较Tab.4 Comparison of displacement time history response under rare earthquake
由表4不难看出,在8度罕遇地震下,结构1-3层最大弹塑性水平位移相差不大,复合筋框架结构3层以上最大弹塑性水平位移较普通钢筋混凝土框架结构有明显减小;层间弹塑性转角最大值发生在第2、3层,其次是底层,3层以上依次递减。总体看来,模型2比模型1的层间转角分布更均匀,位移响应更小。
图8、图9给出了两个框架模型在罕遇地震下的顶层水平位移和二层弹塑性层间转角的时程响应对比。

图8 顶层水平位移时程反应比较Fig.8 Comparison of the maximum story drift between two models

图9 二层弹塑性层间转角比较Fig.9 Comparison of the second story drift angle between two models
图8、图9不难看出,由于复合筋具有一定的二次刚度,使得复合筋框架结构在大震下具有良好的震后残余位移。
4.3 塑性铰分布
以纵向受力筋材应力首次达屈服应力或应变首次达屈服应变为出现塑性铰标志。模型1和模型2在EL Centro波8度罕遇地震下梁柱端部出铰时刻及位置如图10所示,杆端数字表示出铰时刻,单位为s。

图10 EL Centro波罕遇地震下杆端出铰时间图Fig.10 The appearing times of plastic hinges under the rare earthquake ground motion of EL Centro wave
从图10可知,在罕遇水准地震下,模型1和模型2除底层个别柱根出现塑性铰外所形成的大多为梁端塑性铰,梁铰分布较为广泛。从两个框架模型出铰的时刻、位置、数量比较来看,在相同条件下模型2的杆端出铰时间相对更晚、数量更少。这是由于钢-玄武岩纤维复合筋的二次刚度导致构件刚度退化较慢,延迟了出铰时间;构件耗能能力增强导致了模型2出铰数量也相对较少。总体来看,钢-玄武岩纤维复合筋框架结构在大震下的损伤控制效果明显,具有较好的震后可修复性,更易形成梁铰塑性耗能机制。
5 结 论
本文开展了钢-玄武岩纤维复合筋混凝土框架结构的非线性地震反应研究工作。结论如下:
(1)在多遇和罕遇地震动输入下,配置钢-玄武岩纤维复合筋混凝土框架结构的最大弹塑性位移与层间转角等指标比普通钢筋混凝土框架结构有所减小;结构自振周期变化率可作为评价结构整体损伤程度的指标;在罕遇水准的地面运动输入下,钢-玄武岩纤维复合筋混凝土框架结构自振周期变化率明显小于RC框架结构,结构刚度退化和损伤程度小,耗能能力更好,杆端出铰时间相对更晚、数量更少且更易形成梁铰塑性耗能机制。
(2)在罕遇地震下,由于钢筋屈服后构件端部出铰产生较大塑性变形,钢筋混凝土框架会产生较大的残余位移,这种残余位移可使结构不能正常使用甚至由于重力二阶效应而倒塌。配置具有一定二次刚度的钢-玄武岩纤维复合筋能够起到有效控制框架结构的弹塑性变形,减小结构的残余位移,从而可以改善结构在大震下的性能确保大震不倒的安全性能目标。
(3)钢-玄武岩纤维复合筋可充分利用材料的强度,可用于混凝土框架结构设计,通过合理配置钢筋与玄武岩纤维的比例来满足框架结构的延性设计要求,在条件恶劣的环境下有较好的应用前景。
[1]吴刚,罗云标,吴智深,等.钢-连续纤维复合筋(SFCB)力学性能试验研究与理论分析[J].土木工程学报,2010,43(3):53-61.
WUGang,LUOYun-biao,WUZhi-shen,etal.Experimental and theoretical studies on mechanical properties of steel-FRP compos ite bars(SFCB)[J].China Cvil Engineering Journal,2010,43(3):53-61.
[2]罗云标.钢-连续纤维复合筋及其增强混凝土结构性能研究[D].南京:东南大学,2008.
[3]Sun Z Y,Wu G,Wu Z S,et al.Seismic behavior of concrete columns reinforced by steel-FRP(fiber-reinforced polymer)composite bar[J].J Compos Constr,2011,15(5):696 -706.
[4]汪训流,叶列平,陆新征.往复荷载下预应力混凝土结构的数值模拟[J].工程抗震与加固改造,2006,28(6):25 -29.
WANG Xun-liu,YE Lie-ping,LU Xin-zheng,Numerical simulation for the hysteresis behavior of pre-stressed concrete structures under cyclic loads[J].Earthquake Resistant Engineering and Retrofitting,2006,28(6):25-29.
[5]Menegotto M,Pinto P E.Method of analysis of cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under normal force and bending[R].Lisbon,Portugal:Preliminary Report,IABSE,1973,13:15-22.[6]Kent D C,Park R.Fl exural members with confined-concrete [J].Journal of the Structural Division,1971,97:1969 -1990.
[7]Scott Michael H,Fenves Gregory L.Plastic hinge integration methods for force-based beam-column elements[J].Journal of Structural Engineering,2006,132(2):244-252.
[8]刘如驰.用于抗震能量分析的混凝土框架杆系模型[D].南京:东南大学,2012.
[9]陈滔,黄宗明.基于有限单元柔度法的钢筋混凝土空间框架非弹性地震反应分析[J].建筑结构学报,2004,25(2):79-84.
CHEN Tao,HUANG Zong-ming,Flexibility based finite element method for inelastic seismic response analysis of reinforced concrete space frames[J].Journal of Building Structures,2004,25(2):79-84.
[10]高芳清,金建明,高淑英.基于模态分析的结构损伤检测方法研究[J].西南交通大学学报,1998,33(1):108-113.
GAO Fang-qing,JIN Jian-ming,GAO Shu-ying,Damage detection in structures by modal analysis[J].Journal of Southwest Jiaotong University,1998,33(1):108-113.
Nonlinear seismic response analysis of a concrete frame structure reinforced with steel-basalt fiber composite bars
XIAO Tong-liang,QIU Hong-xing,TAO Xin,SUN Jian,CHEN Chun-chao
(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education,Southeast University,Nanjing 210096,China)
Steel-fiber-reinforced polymer composite bar(SFCB)is a new kind of reinforcing material.It has some excellent properties,such as,corrosion-resistance and stable post-yield stiffness.Here,the nonlinear seismic response analysis of a steel-basalt fiber composite bars concrete frame was performed including deducing the flexibility matrix of the bar element based on Gauss-Radau integral method and using this matrix for nonlinear time history response analysis of the frame structure.A RC frame and a corresponding SFCB concrete frame were designed in na area subjected to 8 earthquake according to the current code for design of concrete structures.Their aseismic performance indexes,including rates of natural vibration period,nonlinear time history response,and when and where the plastic hinge emerged were compared.The results showed that the SFCB frame has smaller interlayer displacement angle and maximum elasto-plastic displacement than the RC frame does under the frequent and rare earthquake ground motions;under the rare earthquake ground motion,the SFCB frame has a smaller rate of natural vibration period than the RC frame does,with even slighter stiffness degradation and damage level;furthermore,fewer plastic hinges appear at the ends of the members in the SFCB frame at a relatively later time,it is easier to form the beam-hinge plastic energy dissipation mechanism;the steel-basalt fiber composite bars can make full use of the strength of materials by appropriately deploying steel bar and basalt fiber to effectively control the plastic deformation of the frame and decrease the residual displacement of the frame structure,and thus to reduce the gravity second-order effect on columns and improve the aseismic performance of the whole structure.
steel-basalt fiber composite bars;reinforced concrete(RC)frames;time history analysis;post-yield stiffness;nonlinear response
TU375.3
A
10.13465/j.cnki.jvs.2014.23.031
国家自然科学基金项目(51078077)
2013-09-12
肖同亮男,博士生,讲师,1982年生
邱洪兴男,博士,教授,1962年生
