机械式硫化机开合模过程运动学优化

翟 鹏，王 萌，肖加海，张洪洋

（山东大学（威海）机电与信息工程学院，威海 264209）

机械式硫化机开合模过程运动学优化

翟 鹏，王 萌，肖加海，张洪洋

（山东大学（威海）机电与信息工程学院，威海 264209）

针对机械式硫化机在开合模过程中的横梁会产生明显的运动冲击问题进行了运动学分析，提出了基于加速度连续的主导轨曲率变化规律曲线，建立了数学模型，并基于CATIA软件进行了仿真研究及优化设计；将最终确定的优化导轨曲线用CATIA＿CAM生成相应加工程序，完成硫化机墙板上横梁导轨的数控成形，实际应用于硫化机的设备大修，降低横梁系统冲击77%以上，基本上消除了原硫化机运行过程的冲击问题。目前硫化机制造企业已用该方法大修设备3台，实际运行于生产现场，取得了较好的效果。

运动仿真；CATIA；二次开发；运动冲击

在国内外轮胎的生产制造过程中，轮胎定型硫化机运行的稳定性决定着轮胎的成型精度，是影响轮胎实际使用性能的关键性设备［1］。目前现有的B型垂直平移机械式硫化机普遍存在的一个困扰多年的技术难题：B型垂直平移式机械式硫化机在开模与合模的过程中横梁下面吊挂着硫化室上模块，在运动过程中会产生一个比较明显的运动冲击，造成横梁带着硫化室将产生明显的整体晃动，影响轮胎成型精度及硫化机使用寿命。

影响硫化机运行平稳性的因素是综合性的，并且不同程度上受到制造精度和装配精度的影响［2］，比如益阳橡胶厂通过增大总传动比和主辊轮采用轴承等方式可以减轻横梁向左右侧滑的情况，对减轻横梁在墙板导轨上晃动的问题取得了一定的效果；银川佳通轮胎有限公司提出利用传动螺钉和滑块限制横梁的左右摆动，避免其向单侧横移，也未能解决开合模过程的晃动问题［3］。其他相关的科技文献（如凸轮的设计和异性腔体或者叶片的设计等［4］）在解决运动冲击问题时一般采用建立数学模型，分析其加速度变化，再根据运动学要求反求曲线的方法，然而对本文研究的机械式硫化机由于难以建立数学模型，准确计算横梁的运动参数，所以该方法并不适合。

本文没有采用传统的建立数学模型分析横梁运动，而是提出了结合运动仿真的CAE优化设计思想，研究了影响B型垂直平移机械式硫化机运行平稳性的关键因素，讨论了基于数字化建模和虚拟装配的运动分析，并根据运动学规律依托CATIA二次开发模块设计出新的墙板曲线，并通过建立虚拟样机运动分析检验新设计的运行结果，最后依靠轮胎公司实际制造出改进的硫化机墙板曲线，并在曲柄齿轮和连杆等其他零部件不变的情况下进行硫化机整体装配，结合工厂的实际运行情况验证墙板曲线效果。试验情况表明：优化设计的墙板曲线较好地解决了B型垂直平移机械式硫化机的横梁晃动问题［5－7］，取得了良好的实际效果。

1 硫化机虚拟样机运动分析

1.1 硫化机开合模运动情况

机械式硫化机开合模运动一般是由电机经减速机、减速齿轮、曲柄齿轮、连杆等进行传动。其传动结构如图1。

图1 机械式硫化机结构Fig．1 Mechanical vulcanizer structure

1.2 机械式硫化机的运动仿真机制建立

在整个运动系统中，墙板可以视为凸轮构件，墙板与横梁滚子构成了移动高副。本文研究的机械式硫化机中最重要也最为复杂的“墙板－滚子高副”使用“滚动曲线”接合来定义，利用CATIA DMU模块建立虚拟样机如图2。

图2 机械式硫化机虚拟样机Fig．2 Mechanical vulcanizer virtual prototype

B型垂直平移机械式硫化机在开模过程中，横梁放置在上滑台起始位置，墙板的主导轨由一段与水平成6°的倾斜线L0，两段相切的过渡圆弧R0，R1和一条与水平线垂直的直线导轨L1组成，如图3。

硫化机墙板作为机架，滚子中心作为运动参考点，根据动力学公式F＝ma，则加速度的变化是反应横梁受力情况的最重要参数。经观察可知：在这个仿真过程中会有三个位置加速度产生突变，在此称为加速度尖点位置采集得到加速度如图4。

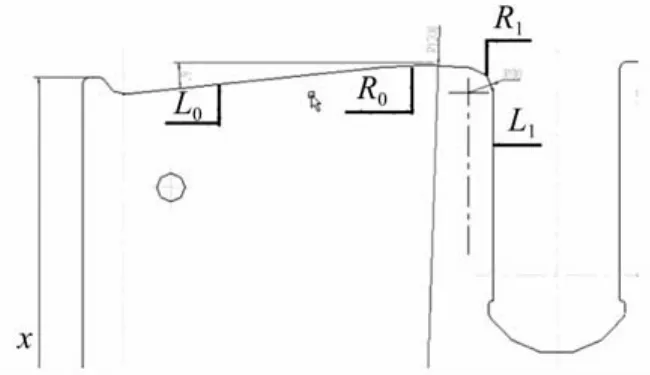
图3 墙板主导轨二维图Fig．3 The 2D drawing of main guide rail on wall board

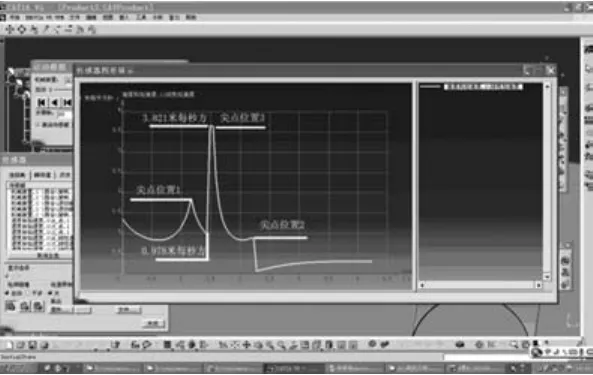
图4 修改前模型滚子中心加速度Fig．4 The accelaration before modification

在当虚拟样机运行到1．23 s时会产生第一个加速度尖点，此时滚子运动到墙体6°倾斜直线L0与R0＝1 300交界处，如图5。

图5 修改前加速度尖点位置1：L0与R0＝1 300切点Fig．5 The 1st accelaration cusp before modification：tangency point between L0and R0＝1 300

当虚拟样机运行到2．25 s时加速度会产生尖点位置2，此时滚子运动到R1＝80与竖直线L1交界处，如图6。

图6 修改前加速度尖点位置2：L1与R1＝80切点Fig．6 The 2nd accelaration cusp before modification：tangency point between L1and R1＝80

虚拟样机运行到1．55 s时加速度会产生尖点位置3，此时滚子运动到R0＝1 300与R1＝80两段过渡圆弧的交界处，如图7。

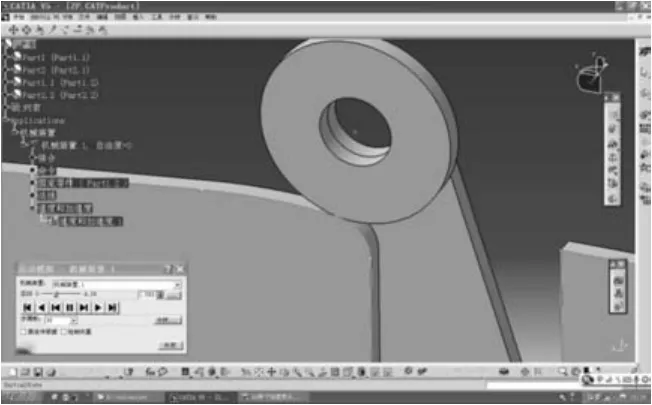
图7 修改前加速度尖点位置3：两过渡圆弧交界处Fig．7 The 3rd accelaration cusp before modification：tangency point between two transition curves

当虚拟样机运行到1．55 s时加速度会产生合模过程中最大的波动，根据动力学公式F＝ma，则横梁由于运动加速度由0．978 m／s2突然提高到3．821 m／s2，加速度的突变为2．743 m／s2会产生一个很大的冲击力。因为根据工厂实际经验的反馈，整个合模过程中只有一次横梁产生很大晃动，由此推测合模过程中横梁带动的上模部分出现的运动冲击会出现在1．55 s滚子运动所在位置。

1.3 运动冲击产生原因分析

横梁在通过了6°直线之后要经过两段过渡圆弧，由于墙体主导轨的两段过渡曲线曲率变化较大，由牛顿第二运动定律F＝ma和径向加速度公式a＝v2／r，向心加速度与运动速度的平方成正比，与曲率半径成反比，而向心力大小与向心加速度大小成正比的基本物理学定律，横梁滚子的加速度与其导轨的曲率成正比。硫化机在经过L0，R0＝1 300，R1＝80，L1的三个切点时曲率都会产生变化，因而为三个理论冲击点，即运动仿真结果中的三个加速度尖点位置。

当滚子在6°直线L0和竖直线L1上运动时，两段直线导轨的曲率为零。所以在两段直线导轨和圆弧的交界处虽然有加速度波动，但是数值比较小，对实际运动效果影响很小。所以在仿真结果上看到的加速度尖点位置1和加速度尖点位置2的加速度突变要远小于加速度尖点位置3，而现场也看不到在直线导轨与圆弧交界处产生运动冲击。现场的情况表明唯一的运动冲击点出现在加速度尖点3，即两段过渡圆弧导轨相切处。

2 新的墙板过渡曲线设计

根据轮胎公司的要求，整套机械式硫化机在返修过程中，曲柄齿轮、连杆和滚子以及横梁等部件由于其本身为标准件或者难以加工等原因不适合修改尺寸，希望保持这些运动构件所有尺寸不变。而墙板零件可以在数控铣床上进行加工，或者利用补焊来增加特定位置的厚度，易于修改。本着满足客户需求和减小工程难度的原则，本文只修改墙体主导轨尺寸，而保持其他运动构件尺寸不变，将主导轨过渡曲线上的两条圆弧过渡曲线优化成为一条曲率半径缓慢变化的过渡曲线。

将主导轨过渡曲线上的两条圆弧过渡曲线优化成为一条曲率半径缓慢变化的过渡曲线。将原有的两段过渡圆弧改进为m段圆弧半径按照递减规律均匀地过渡，如：R1，R2，R3，R4，…，Rm－1，Rm。具体的曲率变化情况根据不同的机型有不同的要求，比如参照凸轮摆线的设计规律，设计起始圆弧R1＝1 300至终止圆弧Rm＝80圆弧半径按照等余弦的方式均匀下降：

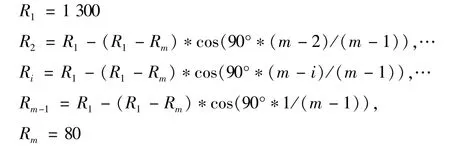
这样设计可以实现墙体曲线的平滑过渡，半径过渡次数m取得越大，则过渡曲线就显得越均匀。当m取得无穷大的情况下，可以实现过渡曲线的G2连续。考虑到工程实际需要和现有实验室计算机的运算能力，给m选取一个比较大的数值，则圆弧曲率和向心加速度变化就能平滑过渡，从而实现机械式硫化机的平稳运行。但是利用传统的绘图方法手工计算量大（需要不断计算新的过渡圆弧半径和圆心位置）、效率低，且难以实现大量圆弧相切和按规律递减等目标，本文采用CATIA V5二次开发的方法设计一段曲率连续的墙板主导轨过渡曲线。

2.1 基于CATIA二次开发技术设计墙板过渡曲线

绘制m段连续相切的圆弧相关代码如下。

设置全部过渡圆弧段数：

m＝100'm设置的越大，主导轨过渡曲线越平滑。

CATIA中绘制圆弧的基本语法为：

CreateCircle（double iCenterX，double iCenterY，double iRadius，double iStartParam，double iEndParam）As

CATIACircle2D

其中，iCenterX，iCenterY是圆弧中心坐标；

iRadius为圆弧半径；

iStartParam是圆弧起始圆心角，必须以弧度表示；

iEndParam是圆弧终点圆心角。这些变量都是双精度型。

墙体主导轨由6°斜线变化到垂直于水平直线的90°直线，共变化96°如图8。

斜线变第i个过渡圆弧的过渡半径为：

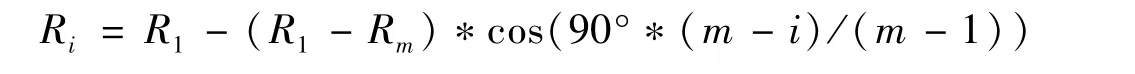
第i个切点坐标为：

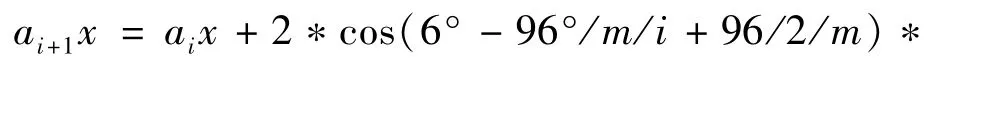
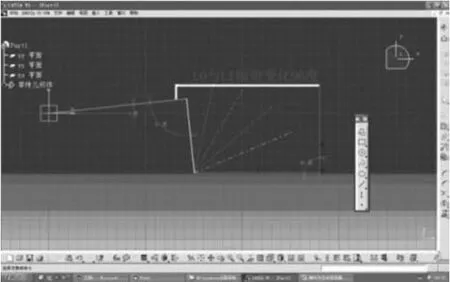
图8 L0与L1倾角变化为96°Fig．8 96 degree transition angle between L0and L1

将其他图元依次画好之后，基于二次开发技术生成的零件草图如图9。

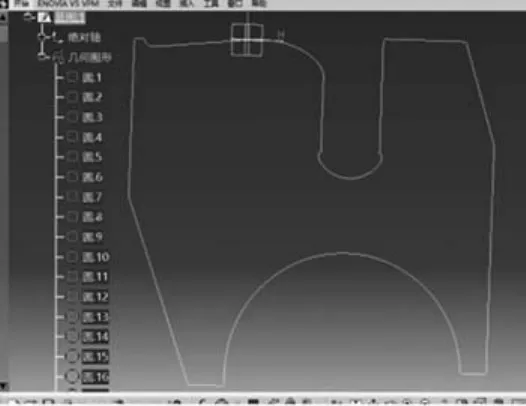
图9 基于二次开发的方法生成的零件草图Fig．9 Part drawing produced by CATIA second development

2.2 新墙板过渡曲线优化模型运动仿真

根据本章前面提到的设计修改要求，在曲柄齿轮、连杆、滚子等运动构件尺寸和位置关系不变的条件下，利用二次开发技术生成的新的墙板零件进行装配，重新建立虚拟样机，设置与原来相同的转速，得到的加速度图。经观察可知：在整个机构也会产生两个加速度尖点位置如图10。

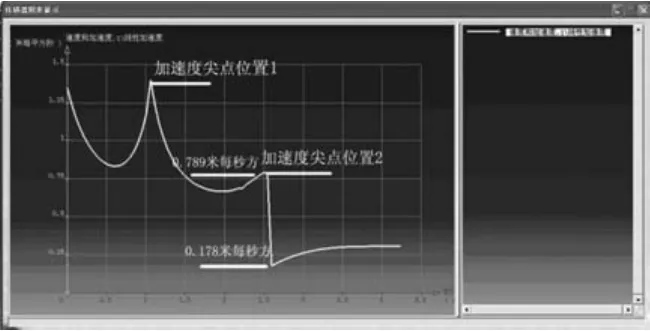
图10 “m段过渡圆弧”优化后的加速度Fig．10 Accelaraion modified by m transition curves

当虚拟样机运行到1．10 s时会产生第一个加速度尖点，滚子的加速度会由0．833 m／s2较快地提高1．398 m／s2，加速度波动为0．565 m／s2产生的加速度尖点位置为6°直线L0与R1＝1 300过渡圆弧的交界处，如图11。

图11 m段过渡圆弧加速度尖点位置1：L0与R1＝1 300切点Fig．11 The 1st accelaration cusp on m transition curves：tangency point between L0and R1＝1 300

当虚拟样机运行到2．52 s时会产生第二个加速度尖点，横梁运动加速度由0．789 m／s2突然下降到了0．178 m／s2，加速度波动值为0．611 m／s2，位置为Rm＝80过渡圆弧与竖直线L1交界处，如图12。

图12 m段过渡圆弧加速度尖点位置2：L1与Rm＝80交界处Fig．12 The 2nd accelaration cusp on m transition curves：tangency point betweenL1and Rm＝80

则采用优化设计后的墙板零件组成的硫化机运动机构，其加速度波动由2．743 m／s2下降到了0．611 m／s2，新的加速度波动仅为原来的22．27%，并且在过渡圆弧之间的加速度实现平滑过渡，加速度波动已经消失了。

根据以往的分析经验可知：在直线与过渡圆弧处产生的加速度尖点不会造成横梁的整体晃动的，造成横梁晃动的关键原因是过渡圆弧间的加速度尖点。而新的实验中增加了大量的过渡圆弧，能够实现过渡圆弧的平滑过渡，仿真结果中没有过渡圆弧间的加速度尖点，理论上加速度波动的大为减小可以解决硫化机的运动冲击问题。

3 优化设计后的硫化机墙板加工装配

墙板曲线的草图特征计算定义完成后，基于CATIA 内CAD／CAM的自动化系统确定墙板零件的数控加工工艺。在曲柄齿轮和连杆等其他所有零部件尺寸不变的情况下重新进行装配，电机的转速和减速机减速比不变的条件下运行优化后的B型垂直平移机械式硫化机，实际检验墙板曲线优化后的运行情况，如图13。

用户使用情况表明：整个开模合模过程整套机械式硫化机运行平稳流畅，没有运动冲击产生，说明改进的墙板过渡曲线有效地解决了硫化机开模合模过程中的运动冲击问题。目前用该方法已成功的为用户改造3台设备，使用9个多月中未出现冲击，得到用户的认可。论文提出的研究方法，为其他机械式硫化机改进及类似冲击问题的解决提供了良好的途径。

图13 装配新墙板零件的硫化机Fig．13 The vulcanizer with new wall board

4 结 论

［1］王战江．硫化机参数化集成设计系统开发研究［D］．武汉：华中科技大学，2005．

［2］李金艳．A型轮胎定型硫化机的运动问题分析［J］．轮胎工业，2006，26（3）：174－176．

LI Jin-yan．The analysis of motional issue on A type vulcanizer ［J］．Journal of Tire Industry，2006，26（3）：174－176．

［3］乐卫勤，陈维芳．国内高等级子午线轮胎硫化机的开发现状［J］．橡塑技术与装备，2002，28（10）：6－10．

LE Wei-qin，CHEN Wei-fang．Present developing condition of demostic curing press for high grade radial tire［J］．Journal of China rubber／plastics technology and equipment，2002，28 （10）：6－10．

［4］林立强．异型腔旋叶式计量泵的优化分析与设计［D］．杭州：浙江大学，2011．

［5］龚杰．基于CATIA和ADAMS的汽车变速器参数化设计及仿真［D］．武汉：武汉理工大学，2012．

［6］单岩，谢龙汉．CATIA V5机械设计应用实例［M］．北京：清华大学出版社，2004．

［7］宋永强．机械压力机多连杆机构优化设计及运动仿真研究［D］．济南：山东大学，2011．

Kinematic optimization for opening and closing mold of a mechanical vulcanizer

ZHAI Peng，WANG Meng，XIAO Jia-hai，ZHANG Hong-yang
（College of Mechatronic and Information Engineering，Shandong University，Weihai 264209，China）

The kinematic analysis for beam impact during opening and closing mold of mechanical vulcanizers was presented．Based on a continuous acceleration main guide curve and its curvature varying law，the mathematical model was built and the simulation and optimal design based on CATIA were performed．The determined optimal guide curve was adopted to develop the corresponding processing procedare with CATIA-CAM．The NC forming of the upper beam guide of the vulcanizer wall board was completed and used in vulcanizer overhaul．The beam system impact was reduced by 77% so the impact problem of vulcanizers was basically solved．The proposed method was used in the overhaul of 3 vulcanizers to get a good effect．

kinematic simulation；CATIA；second development；motion impact

TH212；TH213．3

A

10．13465／j．cnki．jvs．2014．23．032

2013－05－08 修改稿收到日期：2013－07－08

翟鹏男，博士，教授，1963年4月生