基于S型曲线轨道的旋转起重机残留摆角抑制

欧阳慧珉，张广明，梅 磊，邓 歆

（南京工业大学自动化与电气工程学院，南京 211816）

基于S型曲线轨道的旋转起重机残留摆角抑制

欧阳慧珉，张广明，梅 磊，邓 歆

（南京工业大学自动化与电气工程学院，南京 211816）

旋转起重机被广泛地用于各种场合来运输沉重物体或有害材料，例如建筑工地，工厂，核设施以及港湾等。由于旋臂的旋转运动会使荷载产生一个二维摆角，因此针对此问题提出一种轨道生成的方式来同时实现旋臂的位置控制和荷载的残留消摆控制。首先，导出一个包含离心力项的起重机部分线性模型。其次，基于该模型通过数值计算生成预先考虑了残留摆角的S型曲线轨道。其中各个参数只需通过求解代数方程即可得到，降低了控制器设计的难度。同时该轨道可以应用于常用的工业控制器中从而降低了系统构建成本。最后，比较仿真和实验结果验证所提方法的有效性。通过使用此法可以实现在无测量摆角的传感器系统情况下准确地操作起重机，从而大大地简化其结构和降低其安装成本。

旋转起重机运动控制残留摆角抑制S型曲线轨道跟踪控制

起重机系统与工业机器人相比，前者使用较少的执行机构和具有较简易的结构，因此被广泛地应用于建筑工地，港湾等场合。特别地，旋转起重机不像桥式起重机那样需要行走轨道等大型设备，所以它们可以应用于像卡车的载物台这样的狭小空间。可是，旋臂的旋转运动会使荷载产生一个二维摆角；因此，操作人员必须具备很高的熟练度来控制起重机使得荷载迅速而准确地到达指定位置。操作上的失误会造成事故，人员伤亡以及破坏周围的环境。

为了减轻操作人员的负担和提高他们工作的安全性，许多研究人员已经为起重机系统开发了各种各样的控制器。沈滢等［1－2］提出了一种基于坐标变换的旋转起重机直线搬送最优控制方法。欧阳慧珉等［3］提出了一种基于线性矩阵不等式（LMI）的鲁棒控制器。除此之外还包括了滑模变结构控制4］，输入整形控制［5－6］，增益调度控制［7］，基于李亚普诺夫稳定性定理的非线性控制［8］以及模糊控制［9］。

然而，在现存的研究中大多同时利用旋臂的起伏运动和旋转运动来实现消摆控制。如果可以提出一种只利用旋臂的旋转运动即无需其起伏运动而实现消摆控制方法的话，就可以实现无需控制旋臂起伏运动的执行机构的起重机，从而大大地简化了起重机的结构和降低了制造成本。因为旋臂的起伏运动只是用来克服重力的。

但是，当只利用旋臂的旋转运动来消除这个二维摆角时，起重机在目标位置附近的线性化系统则变成不可控制系统。为了解决这个问题，已经有研究者提出了一些方法［10－13］。这些方法主要可分为两种类型：一种是开环控制，即无需摆角信息的轨道生成法［10－11］。另一种是闭环控制，即利用由传感器系统测量到的摆角信息实现消摆控制［12－13］。前者虽然无需额外的传感器系统，但是大多生成较为复杂的轨道从而很难应用于常用的工业控制器中。另一方面，后者虽然可以实现对起重机系统的鲁棒控制，但是需要测量摆角的传感器系统从而增加系统安装难度和成本。

本文将提出一种S型曲线轨道生成法去实现对荷载二维摆角的抑制控制。该轨道可应用于常用的工业控制器中。为实现上述目的，首先，导出一个包含离心力项的起重机部分线性模型。其次，基于该模型通过数值计算生成预先考虑了残留摆角的S型曲线轨道。最后，比较仿真和实验结果验证所提方法的有效性。

1 旋转起重机模型

在如图1所示的旋转起重机模型中，θ1，θ2分别表示旋臂起伏运动平面的摆角和旋转运动平面的切线方向的摆角；θ3，θ4分别表示旋臂的起伏角和旋转角；L，l分别表示旋臂长度和悬绳长度；x，y，z表示荷载的三维空间位置。

图1 旋转起重机模型Fig．1 Schematic model of rotary crane

假设旋转起重机模型具有以下特性：

（1）荷载可以看作是一个质点，且悬绳的扭力可以忽略不计。

（2）仅考虑荷载－悬绳振动系统中的1次振型。

（3）由于摆角θi很小，因此sinθi⋍θi和cosθi⋍1（i ＝1，2）成立。

根据拉格朗日运动方程悬绳和荷载组成的振动系统的动力学方程

由于旋臂旋转运动产生的离心力主要影响着二维摆角，为了导出控制器，对式（1）和式（2）在旋臂到达目标位置附近进行线性化但不包括离心力项和重力项并假设θ很小，使得⋍0，θθ⋍0⋍0⋍

1ij⋍0（i，j＝1，2）成立。在这种情况下，得到其部分线性模型

由式（3）和式（4），得到以下简易模型：

2 轨道生成与结果

2.1 轨道生成

本小节基于式（5）和式（6）所示模型为旋臂的旋转运动生成预先考虑了残留摆角的S型曲线速度轨道。该轨道如图2所示，其中参数t，t，t，分别表示

123加速区间，匀速区间，减速区间以及最高速度。

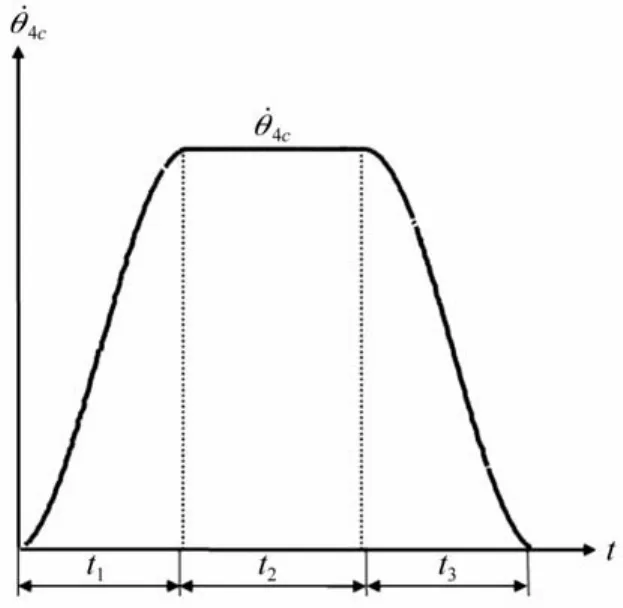
图2 S型曲线速度轨道Fig．2 S-shaped curve velocity trajectory

S型曲线速度轨道

首先，将式（7）代入式（5）中，得到起伏方向摆角θ1在区间t∈［0，t1）上的值θ11为

同理，旋转方向摆角θ2在区间t∈［t1，t1＋t2）上的值θ22为

2.2 轨道生成条件及结果

由于式（15）～式（18）是非线性方程组，因此其数值解取决于它们的初始值。采用列文伯格算法求解并设定最高速度的初始值为0．3 rad／s。加速区间t1与减速区间t3相同，并使其初始值在0．05 s～1．5 s之间变化。旋转角θ4的目标值θ4f分别设定为30°，45°和 60°。匀速区间t的初始值则可由t，t的初始值和

213θ4f求出，结果如表1所示。因为假设荷载固有角频率ωn不变，所以对于不同的θ4f得到了相同的t1，t2，t3。

表1 轨道生成条件及结果Tab.1 Trajectory generation conditions and results

3 仿真与实验

3.1 目标轨道

将式（7）所示S曲线速度轨道进行积分可得到其位置轨道

式中θ4f，Tf分别表示目标角度和最终时间，并设定Tf＝10 s。

3.2 跟踪控制器设计

旋臂的旋转运动可由下式表示：

式中J，d，K，u分别表示旋臂转动惯量，包含非线性力的系统外部干扰，系统参数以及指令电压。式（20）假设旋臂转动惯量J是常量，但是其变化部分可看作系统外部干扰并包含于d。

为了补偿系统外部干扰的影响，将以下所示干扰观测器（DOB）应用于式（20）：

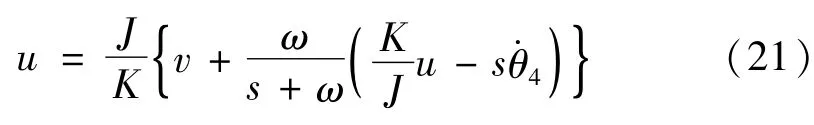
式中s，v，ω分别表示微分算子，由反馈控制器算出新的控制输入以及低通滤波器（LPF）的截止角频率。该控制系统的方框图如图3所示。

图3 含有干扰观测器控制系统Fig．3 Control system with disturbance observer

起重机系统动力学特性在低频区域可表示为下式：

另外，假设目标轨道r的一阶与二阶导数r，r存在并可用于控制器设计。本文采用如下所示的比例微分控制器作为跟踪控制器：

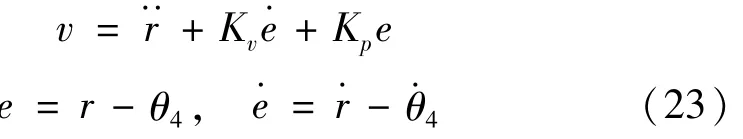
式中Kv，Kp为控制器增益。

将式（23）代入式（22）可得：

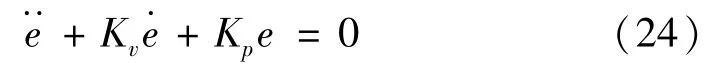
当Kv＞0，Kp＞0时，该系统渐进稳定。本文应用试凑法设定Kv＝50 1／s，Kp＝30 1／s2。

3.3 仿真验证

由于在3．1节中所得出的S型曲线轨道是基于式（5）和式（6）所示模型（以下称作简易模型），因此除了要验证对于简易模型的有效性之外，还要验证其对于式（1），式（2）和式（20）所示模型（以下称作原模型）的有效性。仿真参数如表2所示，其中J，K由电机特性测试实验所得；L，m为设计参数；l为测量所得。

表2 仿真参数Tab.2 Parameters of simulations

首先，基于简易模型的仿真结果如图4－图6所示。图4（c）和图4（d）所示两个方向的摆角都得到很好的抑制，同时图4（a）所示旋转角也与目标轨道一致，并且对于所有的目标角度θ4f都得到几乎相同的结果。

图4 基于简易模型的S型曲线轨道结果（θ4f＝30°）Fig．4 S-shaped curve trajectory results based on simple model（θ4f＝30°）

图5 基于简易模型的S型曲线轨道结果（θ4f＝45°）Fig．5 S-shaped curve trajectory results based on simple model（θ4f＝45°）

图6 基于简易模型的S型曲线轨道结果（θ4f＝60°）Fig．6 S-shaped curve trajectory results based on simple model（θ4f＝60°）

图7 基于原模型的S型曲线轨道结果（θ4f＝30°）Fig．7 S-shaped curve trajectory results based on original model（θ4f＝30°）

图8 基于原模型的S型曲线轨道结果（θ4f＝45°）Fig．8 S－shaped curve trajectory results based on original model（θ4f＝45°）

其次，验证所提出轨道对原模型的有效性。式（20）所示外部干扰d不仅包括非线性力还包括了如下所示摩擦项：

式中C，fn分别表示粘性摩擦系数，静摩擦或库伦摩擦。fn的属性为

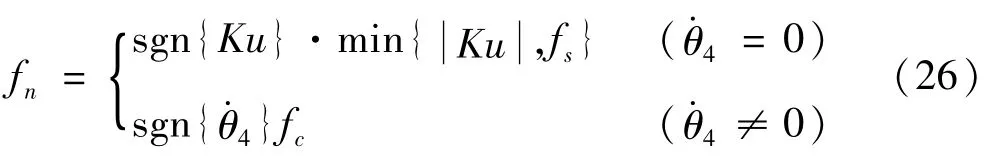
式中fs，fc分别表示静摩擦和库伦摩擦，其值为C＝1．39 Nm／（rad／s），fs＝3．71 Nm，fc＝3．58 Nm。

采用图3所示的含有干扰观测器的控制系统对摩擦项进行补偿并作仿真分析，其结果如图7～图9所示。

另外，本文所提出的S型曲线轨道分别应用于简易模型，原模型（不含干扰观测器）以及原模型（含干扰观测器）时的旋转角平均稳态误差，最大起伏残留摆角和最大旋转残留摆角如表3～表5所示。

由图4～图9以及表3～表5可知，尽管由于式（1）和式（2）中非线性项以及旋臂驱动系统的摩擦项式（25）的影响，存在于图7～图9中的无论是旋转角稳态误差还是残留摆角振幅都要大于图4～图6中相对应的性能，并且和也会随着旋转角速度的增大而增大。但是，通过使用含有干扰观测器的控制系统不仅减少了旋转角的稳态误差，也加强了摆角的抑制效果，并将其控制在很小的范围内了。

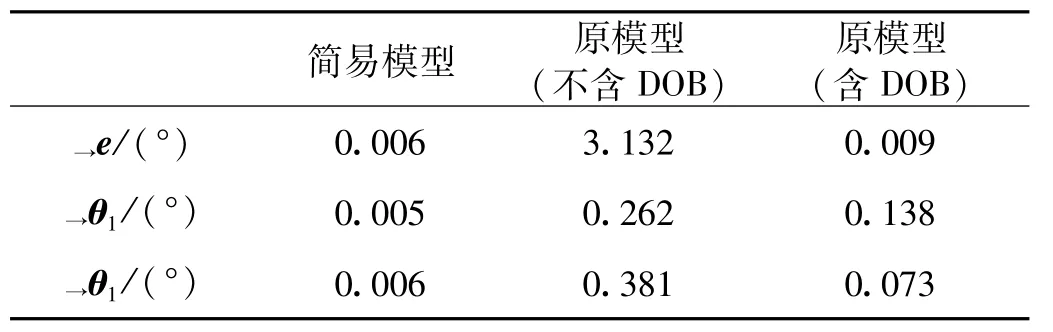
表3 仿真结果比较（θ4f＝30°）Tab.3 Comparison of simulation results（θ4f＝30°）

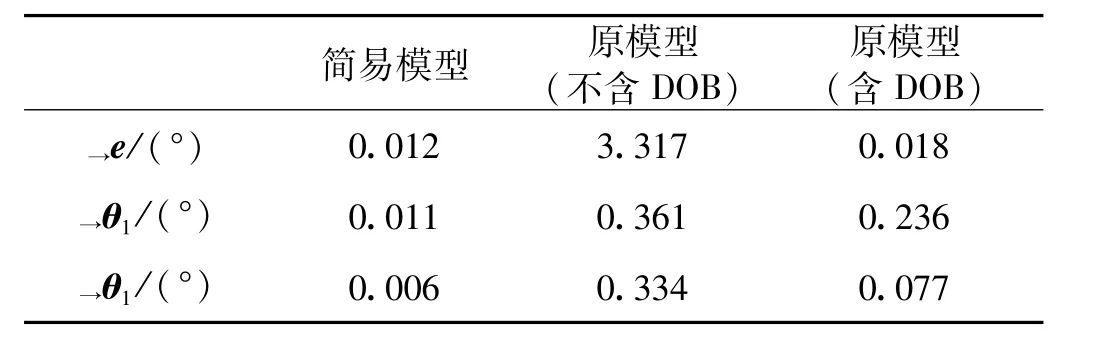
表4 仿真结果比较（θ4f＝45°）Tab.4 Comparison of simulation results（θ4f＝45°）

图9 基于原模型的S型曲线轨道结果（θ4f＝60°）Fig．9 S-shaped curve trajectory results based on original model（θ4f＝60°）

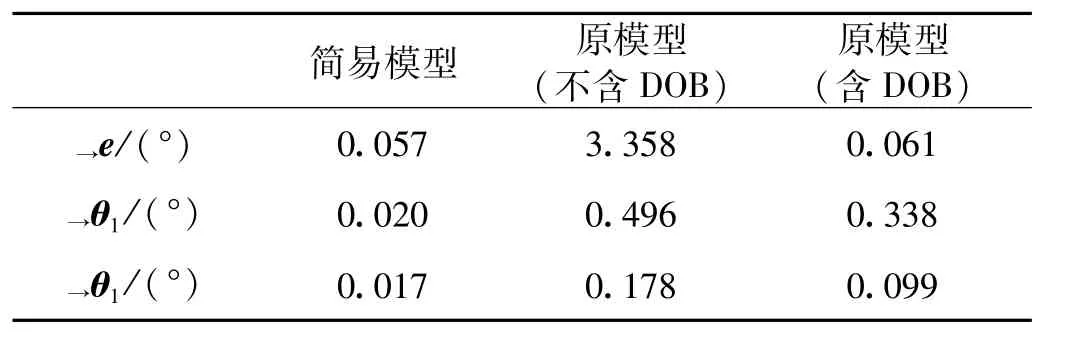
表5 仿真结果比较（θ4f＝60°）Tab.5 Comparison of simulation results（θ4f＝60°）

3.4 实验设备

如图10所示的系统由驱动旋臂起伏和旋转运动的直流电动机，旋臂，悬绳，荷载等部分构成。旋转角可由编码器测得，其角度测量分辨率为1．8×10－3。在本文中，仅使用驱动旋臂旋转运动的电机，即电机2。

测量摆角的传感器系统如图11所示。测量起伏方向摆角θ1的电位计1固定在旋臂上。测量旋转方向摆角θ2的电位计2固定在部件1上，并围绕电位计1的旋转轴旋转。部件2和长杆共同围绕电位计2的旋转轴旋转。部件3相对于长杆，部件4相对于部件3分别旋转。部件4可沿着悬绳滑动。其角度测量分辨率为6．4×10－2。在本文中，该系统仅用来观测摆角。

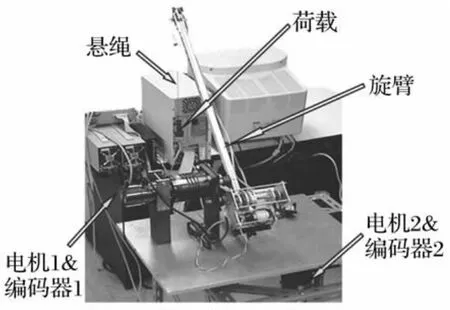
图10 实验系统Fig．10 Experimental system

图11 测量摆角的传感器系统Fig．11 Sensor system for measuring load sway

另外，实验设备各组件型号等参数如表6所示。

表6 实验设备组件Tab.6 Elements of experimental apparatus

3.5 比较实验

本小节通过比较实验进一步验证本文中所提出的S型曲线轨道的有效性。实验参数与仿真参数相同。

用于比较的摆线轨道如下所示：

式中θ0，θ4f，ts，Tf分别表示初始角度，目标角度，到达时间，终了时间，并设定为θ0＝0°，θ4f＝45°，ts＝5 s，Tf＝10 s。其结果如图12所示。在图12（a），（b）和（d）中实验结果与仿真结果几乎一致。然而在图12（c）中，实验结果与仿真结果之间存在的差异是由于悬绳与旋臂顶端之间的摩擦所造成的，该摩擦因素使得起伏方向的摆角θ1发生了衰减。

S型曲线轨道的结果如图13所示。虽然与图12一样起伏方向摆角θ1也发生了衰减，但是很明显S型曲线轨道更好地抑制了旋转方向摆角θ2，同时比摆线轨道要快0．6 s到达目标位置。

当目标角度θ4f分别为30°和60°时的结果如图14和图15所示，并得到与θ4f＝45°时几乎相同的结果。

表7 实验结果比较（θ4f＝45°）Tab.7 Comparison of experimental results（θ4f＝45°）

图12 摆线轨道结果（θ4f＝45°）Fig．12 Cycloid curve trajectory results（θ4f＝45°）

图13 S型曲线轨道结果（θ4f＝45°）Fig．13 S-shaped curve trajectory results（θ4f＝45°）

图14 S型曲线轨道结果（θ4f＝30°）Fig．14 S-shaped curve trajectory results（θ4f＝30°）

图15 S型曲线轨道结果（θ4f＝60°）Fig．15 S-shaped curve trajectory results（θ4f＝60°）

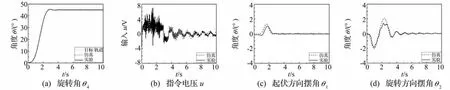
图16 闭环控制方式结果（θ4f＝45°）Fig．16 Closed-loop control results（θ4f＝45°）

3.6 闭环控制方法

为了进一步验证S型曲线轨道的有效性，本小节将基于李雅普诺夫稳定性定理的非线性反馈控制器用于与本文相同的起重机系统实现摆角的消摆控制［14］。在文献［14］中，为了对旋臂驱动系统摩擦项的补偿从而可以获得良好的旋转角跟踪特性，采用了与3．2节相同的干扰观测器。其次，基于起重机简易模型设计了一种非线性变结构控制器，该方法不仅反馈了旋转角及其角速度而且还利用了两个方向的摆角及其角速度信息。其仿真和实验结果如图16所示。

另外，摆线轨道，S型曲线轨道以及闭环控制法分别应用于起重机系统时的旋转角平均稳态误差，最大起伏残留摆角，最大旋转残留摆角以及到达时间如表7所示。

由图12，图13，图16以及表7可知，因为使用了摆角的信息，所以闭环控制法获得了较短的运送时间，但是荷载搬送中的摆角要大于前种方法。因此也证明了即使不使用摆角信息且仅用S型曲线轨道同样可以获得很好的旋臂定位精度和摆角抑制效果。

4 结 论

本文的目的是在不使用测量摆角的传感器的前提下只使用旋臂旋转运动实现起重机消摆控制。为此，首先导出了一个包含离心力项的起重机部分线性模型。其次，基于该模型通过数值计算生成了预先考虑了残留摆角的S型曲线轨道。其中各个参数只需通过求解代数方程即可得到，降低了控制器设计的难度。最后，比较仿真和实验结果验证了该方法的有效性。该轨道可以应用于常用的工业控制器中从而降低了系统构建成本，同时也为简化起重机结构和增加其安全性提供了一种可能。该控制方法可适用于其他类似的起重机模型，具有一定的普遍性。

然而，在实际的起重机操作过程中悬绳长度的变化会影响控制系统的稳定性以及控制性能，接下来将该方法扩展到绳长变化的情况。

［1］Terashima K，Shen Y，Yano K．Modeling and optimal control of a rotary crane using the straight transformation method［J］．Control Engineering Practice，2007，15：1179－1192．

［2］沈滢，曹金城，王玲．旋转起重机建模及负载摆动最优控制［J］．沈阳建筑大学学报（自然科学版），2009，3（25）：605－608．

SHEN Ying，CAO Jin-cheng，WANG Ling．Modeling of a rotary crane and the optimal control for load swing［J］．Journal of Shenyang Jianzhu University（Natural Science），2009，3（25）：605－608．

［3］欧阳慧珉，佐野滋则，内山直树，等．基于LMI的旋转起重机鲁棒控制器设计［J］．振动与冲击，2014，33（1）：106 －112．

OUYANG Hui-min，SANO S，UCHIYAMA N，et al．Robust controller for rotary cranes based on LMI［J］．Journal of Vibration and Shock，2014，33（1）：106－112．

［4］Almutairi N B，Zribi M．Sliding mode control of a threedimensional overhead crane［J］．Journal of Vibration and Control，2009，15（11）：1679－1730．

［5］董明晓，孙杰，郑康平，等．闭环输入整形器消除多模态柔性系统残留振荡［J］．机械工程学报，2006，42（5）：110－114．

DONG Ming-xiao，SUN Jie，ZHENG Kang-ping，et al．Closed-loop input shaper eliminating residual vibration of multi-modeflexiblesystems［J］．ChineseJournalof Mechanical Engineering，2006，42（5）：110－114．

［6］Lawrence J，Singhose W．Command shaping slewing motions for tower cranes［J］．ASME Journal of Vibration and Acoustics，2010，132（91）：1－11．

［7］Omar H M，Nayfeh A H．Gantry cranes gain scheduling feedback control with friction compensation［J］．Journal of Vibration and Control，2005，281：1－20．

［8］Yazied T G，Hagag S Y，Ajmi M S，et al．Nonlinear modelling and vibration control of jib cranes［J］．World Applied Sciences Journal，2012，16（11），1543－1550．

［9］Wang Xiao-jun，Shao Hui-he．Hybrid control approach for container cranes［J］．ChineseJournalofMechanical Engineering（English Edition），2005，18（3）：351－355．

［10］Ohto M，Yasunobu S．A rotary crane control method based on a skillful operator's knowledge［J］．Transactions of the Society of Instruments and Control Engineers（In Japanese），1997，33（9）：923－929．［11］Kondo R，Takeda T，Taguchi H，et al．Sway control for rotary crane based on load swing period［J］．Transactions of the JapanSocietyofMechanicalEngineers（C）（In Japanese），2000，67（655）：725－731．

［12］Nakazono K，Ohnishi K，Kinjo H，et al．Vibration control of load for rotary crane system using neural network with GA-based training［J］．Artificial Life and Robotics，2008，13：98－101．

［13］Kondo R，Shimahara S．Anti-sway control of a rotary crane via two-mode switching control［J］．Transactions of the Society of Instruments and Control Engineers（In Japanese），2005，41（4）：307－331．

［14］欧阳慧珉，内山直树，佐野滋则，等．只利用旋臂旋转运动的起重机消摆控制［J］．振动与冲击，2014，33（4）：131 －137．

OUYANG Hui-min，UCHIYAMA N，SANO S，et al．Load swaysuppressioncontrolforrotarycranesusingonly horizontal boom motion［J］．Journal of Vibration and Shock，2014，33（4）：131－137．

Residual load sway suppression for rotary cranes based on an S-shaped curve trajectory

OUYANG Hui-min，ZHANG Guang-ming，MEI Lei，DENG Xin
（College of Automation and Electrical Engineering，Nanjing Tech University，Nanjing 211816，China）

Rotary cranes are widely used to transport heavy loads and hazardous materials in various environments，such as，shipyards，factories，nuclear installations，and construction sites．Because horizontal motion of booms in rotary cranes typically generates an undesirable two-dimensional load sway，a trajectory generation method was proposed to realize boom positioning control and residual load sway suppression．Firstly，a partial linearized dynamic model of a rotary crane including a centrifugal force term responsible for the two-dimensional load sway was derived．Next，an S-shaped curve trajectory suppressing residual load sway was generated with the numerical calculation method．The parameters of the trajectory were obtained only by solving algebraic equations．This trajectory was applied to conventional industrial controllers for reducing their system construction cost．Finally，comparing the results of simulations and tests demonstrated the effectiveness of the proposed method．Thus，the crane could be precisely operated without sensor systems for measuring load sway，the structure of the crane was simplified and its installing cost was reduced．

rotary crane；motion control；residual load sway suppression；S-shaped curve trajectory；tracking control

TH21

A

10．13465／j．cnki．jvs．2014．23．030

国家自然科学基金（51277092）；江苏省基础研究计划（自然科学基金）资助项目（BK20130938）；江苏省高校自然科学研究项目资助（14KJB510013）

2014－06－09 修改稿收到日期：2014－07－23

欧阳慧珉男，博士，讲师，1982年6月