摆线针轮传动线接触弹流润滑分析
2014-05-16孙章栋朱才朝刘怀举刘明勇顾宗琳
孙章栋,朱才朝,刘怀举,刘明勇,顾宗琳
(重庆大学机械传动国家重点实验室,重庆 400030)
摆线针轮传动线接触弹流润滑分析
孙章栋,朱才朝,刘怀举,刘明勇,顾宗琳
(重庆大学机械传动国家重点实验室,重庆 400030)
对摆线针轮线接触弹流润滑进行数值分析,得出啮合过程中最小膜厚,与经验公式对比,验证模型的正确性。以摆线轮θ=arccosK1处润滑状态作为判断依据,研究载荷、转速和流变指数对摆线针轮传动润滑状态的影响规律。结果表明:随着转速提高,二次压力峰高度降低并向入口区移动,膜厚相应增加;而随着载荷增加,接触区变宽,二次压力峰增加且向出口区移动,膜厚略微减小;流变指数n增加,二次压力峰先增加后减小,最后趋近于Hertz压力,并向出口区移动,膜厚相应减小。讨论了短幅系数k1对润滑的影响,表明在满足设计要求情况下,短幅系数k1减小,有利于提高润滑性能。
摆线针轮;脂润滑;数值解;Ostwald
摆线针轮行星传动以其结构紧凑、传动比大、传动精度高和承载能力大等优点,而被广泛应用。通常使用脂来实现润滑。渐开线齿轮润滑问题已进行广泛的研究,但有关摆线针轮润滑研究少有报道。摆线针轮润滑不同于渐开线:首先摆线针轮传动啮合原理以及几何特征有别于渐开线传动;其次齿摆线轮与针轮同时啮合齿数多于渐开线,同时啮合齿数理论上可以达到一半摆线轮齿数;最后渐开线使用油进行润滑,脂的流变特性有别于油。弹流润滑性能的好坏对摆线针轮传动的性能和使用寿命都有显著影响。开展摆线针轮传动弹流脂润滑数值分析具有重要的意义。
国内外学者对齿轮弹流润滑做了大量研究。Liu[2-3]对线接触直齿轮的混合润滑模型,讨论了转速及不同粗糙度对直齿轮润滑的影响;Zhu等[4]讨论了不同转速工况下由混合润滑过渡到干摩擦接触的润滑情况;Chu等[5]研究了接触面的液面滑移和流体特性对润滑的影响。Yang等[6]对斜齿轮进行弹流润滑分析,讨论了螺旋角对润滑的影响;Liu等[7]首次分析了有限长线接触的热解,并与无限长热解作对比;Zhu等[8]采用有限长线接触模型分析斜齿轮稳态热弹流润滑问题,讨论载荷与转速工况变化对斜齿轮润滑温度及齿面剪切力的影响。刘晓玲等[9]展开对指数率非牛顿流体在线接触条件下的弹流润滑数值研究,应用多重网格法和多重网格积分法数值求解了Newton流体和Ree-Eyring流体线接触等温和热弹流润滑问题。于玫等[10]探讨了不同工况下热效应对脂润滑弹流数值解的影响。李媛等[11]探讨脂润滑条件下激光加工微凹坑表面的摩擦特性,表明适当的凹坑深度可以改善表面的摩擦特性和温度特性。白新瑞等[12]基于有限长线接触弹流润滑理论,求得乏油条件下圆柱滚子轴承弹流润滑的完全数值解。杨沛然等[13]做了大量脂润滑方面的研究工作。
Mihailidis等[14]推导出适合非牛顿流体的乏油广义雷诺方程。由于摆线针轮传动通常是用润滑脂实现润滑,论文以Ostwald模型对摆线针轮传动线接触弹流脂润滑问题进行数值分析研究,研究载荷、转速和流变指数对摆线针轮传动润滑状态的影响规律,讨论设计参数短幅系数k1对润滑的影响。
1 数学模型
1.1 啮合分析
摆线针轮传动同时啮合的齿数多,如图1所示。在啮合过程中,摆线轮曲率半径ρ变化,针齿半径rz为定值,从而可得啮合过程中的当量曲率半径为:
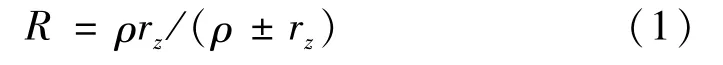
式中“+”号为用于外凸齿廓啮合;“-”号为用于内凹齿廓啮合;ρ为有关啮合相位角的函数。
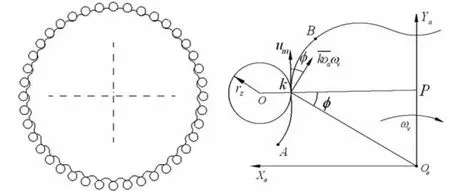
图1 摆线轮与针齿啮合示意图Fig.1 Mathematical model of the cycloid drive
由运动学分析可知,摆线轮与针齿在啮合点处的线速度是相等的,设u1为摆线轮在啮合点处的线速度,u2为针齿在啮合点处的线速度,由图1所示u1=u2=um=,对润滑油的卷吸速度:
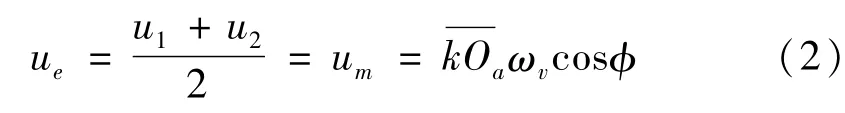
1.2 润滑模型
基于Ostwald模型的润滑脂本构方程为:

式中:m为粘性函数;n为流变指数
采用广义Reynolds方程[15],引入等效粘度η*,对于Ostwald模型,其等效粘度为:
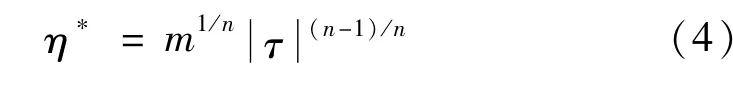
引入等效粘度可将润滑脂的非牛顿流体转换成牛顿流体,方便采用牛顿流体解法求解。利用Hertz接触参数对润滑模型进无量纲化,无量纲量参考量:
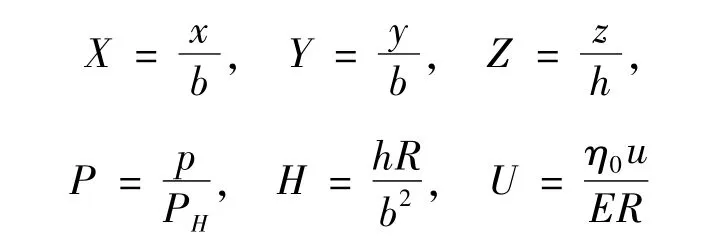
式中x为流动方向,z为膜厚方向,b为Hertz接触半宽,h为油膜厚度,p为油膜压力,PR为最大Hertz压力,R为等效曲率半径,η0为环境粘度,E为等效弹性模量。
无量纲Reynolds方程

式中ρ0为润滑油环境密度。
无量纲Reynolds方程的边界条件为:
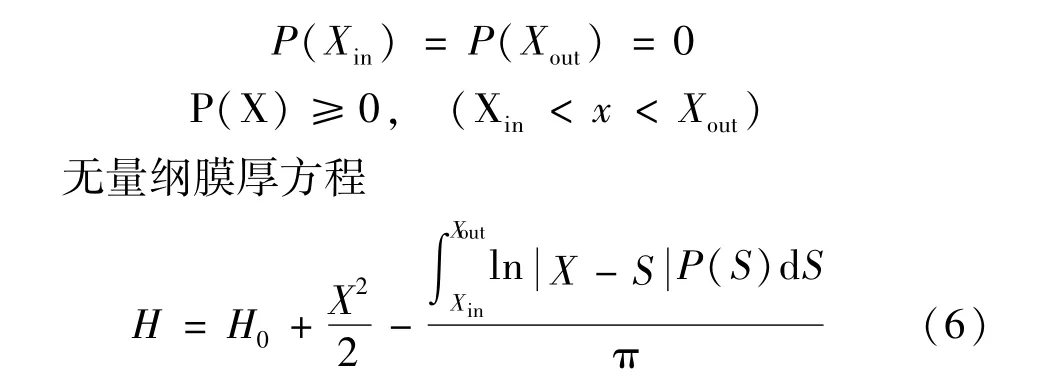
式中H0为常数。
无量纲密度方程
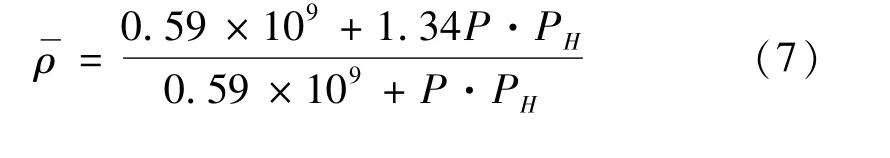
无量纲载荷方程
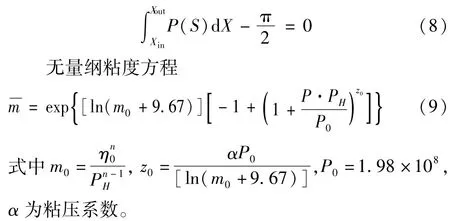
2 线接触弹流脂润滑分析
将式(7)~式(9)离散化,建立摆线针轮传动弹流脂润滑数值仿真模型,通过数值直接迭代法对弹流润滑中的膜厚和压力进行数值求解。Gauss-Seidel迭代法用于求解低压区压力,Jacobi双极子迭代法用于求解高压区压力[16]。
压力求解无量纲计算域范围X=[XinXout]=[-4,1.5],油膜厚度无量纲计算范围Z=[0,1]。X方向的节点数1 025,油膜厚度Z向节点数11。数值迭代精度为:压力相对误差小于10-6。
选取摆线针轮行星传动啮合副为研究对象,其啮合副与润滑相关参数如表1。

表1 摆线针轮传动副与润滑相关参数Tab.1 The cycloid drive parameters and properties of the lubricant
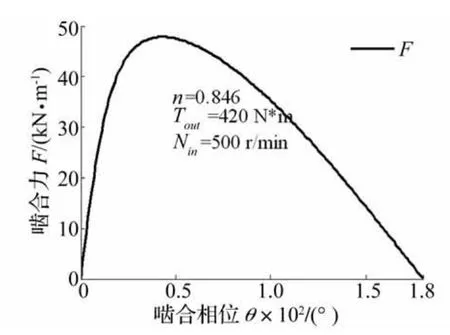
图2 单位啮合力随啮合相位变化Fig.2 The variation of contact force with meshing process
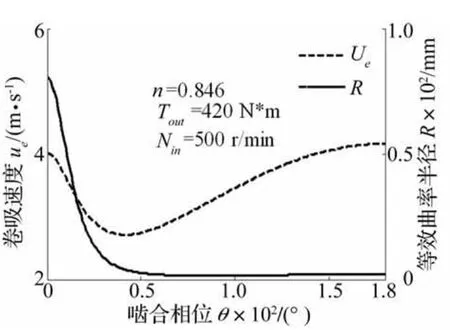
图3 等效曲率半径和卷吸速度变化曲线Fig.3 The variation of reduced curve radius and rolling speed
摆线轮与针齿滚动线接触啮合,在啮合过程中,单位啮合力F、等效曲率半径和卷吸速度随着啮合相位变化。图2给出单位啮合力随啮合相位变化曲线,图3给出卷吸速度和等效曲率半径随啮合相位变化曲线。
设定输入转速500 r/min,输出力矩420 N/m。选取某一啮合相位处进行分析,其润滑脂膜压力、膜厚如图4所示。在出口区处,润滑膜压力出现明显二次压力峰,在二次压力峰相对应处,润滑膜开始收缩,形成出口区的颈缩现象,颈缩处的膜厚为最小润滑膜厚度。摆线轮与针齿滚动啮合剪切应力如图5所示,在润滑膜出口区的颈缩位置出现剪应力峰值,其它区域切应力趋于零值,摩擦小,进一步说明温度对润滑影响小。
摆线轮与针齿理论啮合区间为0°~180°,而实际有效啮合区间为30°~120°。计算最大压力与最小膜厚随着啮合相位变化曲线如图6。如图7所示,与采用Dowson-Higginson润滑油膜厚经验公式计算结果变化趋势相吻合,但比经验公式偏大。由于Dowson-Higginson经验公式用来计算润滑油最小膜厚的,而修形齿廓最小膜厚数值解用来计算润滑脂的,验证数值模型仿真结果正确性。从图2、图3和图7可以得出在啮合相位角θ=arccosK1=42.97°处为曲线拐点,在啮合过程中相位角θ=arccosK1=42.97°时油膜厚度最小,故以此相位处润滑状态作为整个啮合过程中润滑状态的判断依据。

图5 摆线轮与针齿滚动啮合切应力Fig.5 Cycloid gear and pin gear mesh rolling shear stress
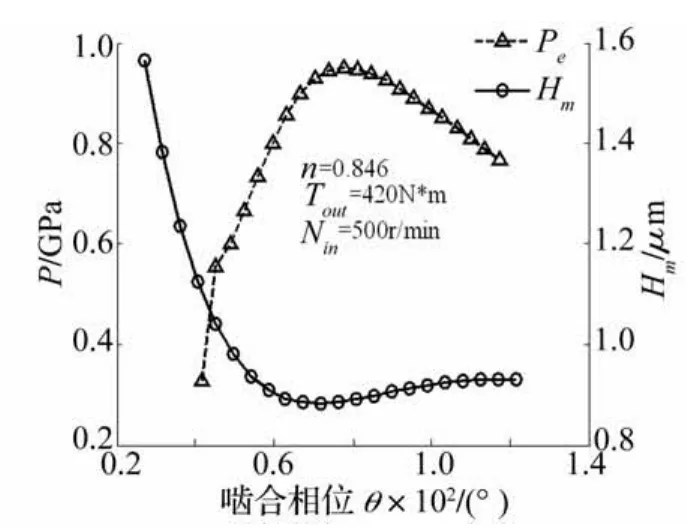
图6 中心压力与最小膜厚随啮合相位变化Fig.6 The variation of center-pressure and min-film thickness
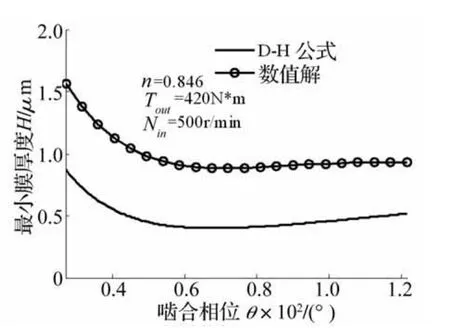
图7 最小膜厚数值解与经验公式比较Fig.7 Compare film thickness numerical solution with empirical formula
3 参数变化对弹流脂润滑的影响
3.1 工况参数变化对润滑影响
图8~9给出了转速变化对θ=42.97°处润滑性能的变化规律。随着转速提高,入口区压力增加,二次压力峰高度减小,其位置向入口区移动,膜厚相应增加,润滑膜平行部分缩短,颈缩变得不明显,表明摆线轮与针齿啮合时,卷吸速度增大,有利于形成良好的弹流润滑膜。
图10~11给出了载荷变化对θ=42.97°处润滑性能的变化规律。随着载荷增加,接触区变宽,入口区压力增加,二次压力峰增加,其位置向出口区移动,膜厚略微减小,膜厚颈缩现象更加明显。主要由于随着载荷增加,油膜刚度变化较小,故膜厚变化不明显。
3.2 流变指数n对润滑影响
图12、13是流变指数n对θ=42.97°处润滑性能的影响规律。当n<1时,随着流变指数n增加,入口区压力降低,二次压力峰增加,并向出口区移动,膜厚相应降低;当n>1时,随着流变指数n增加,入口区压力略微降低,二次压力峰减小并向出口区移动,最后二次压力峰消失,接近Hertz压力,膜厚相应减小,颈缩也越来越不明显,最后消失,润滑状态变差。
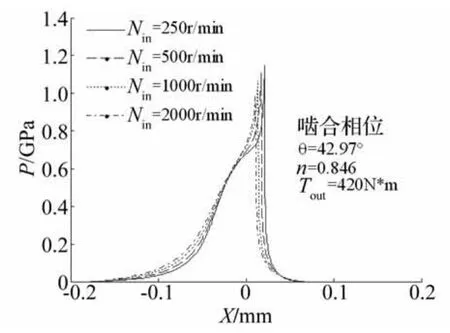
图8 转速对油膜压力分布的影响Fig.8 Pressure distribution for different rotational Speeds
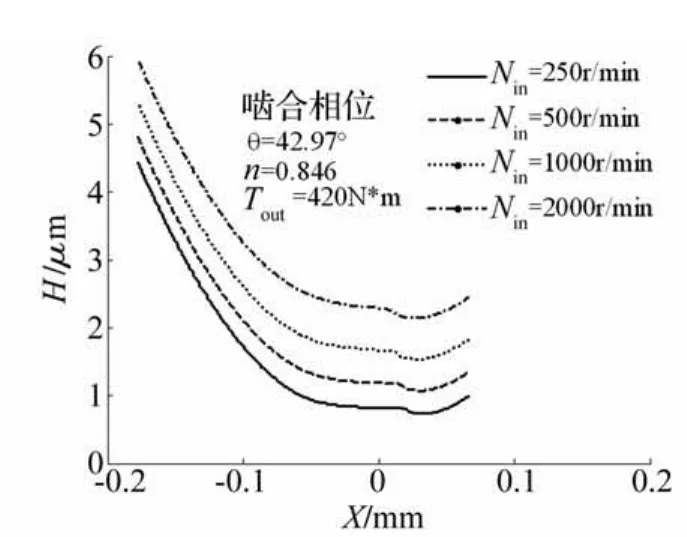
图9 转速对油膜厚度的影响Fig.9 Film shape for different rotational Speeds
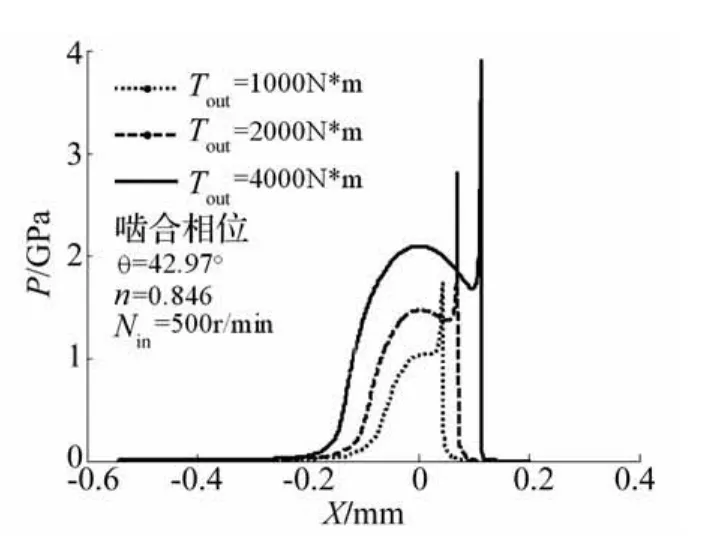
图10 载荷对油膜压力的影响Fig.10 Pressure distribution for different loads
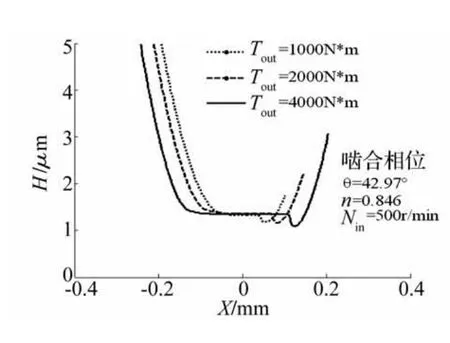
图11 载荷对油膜厚度的影响Fig.11 Film shape for different loads
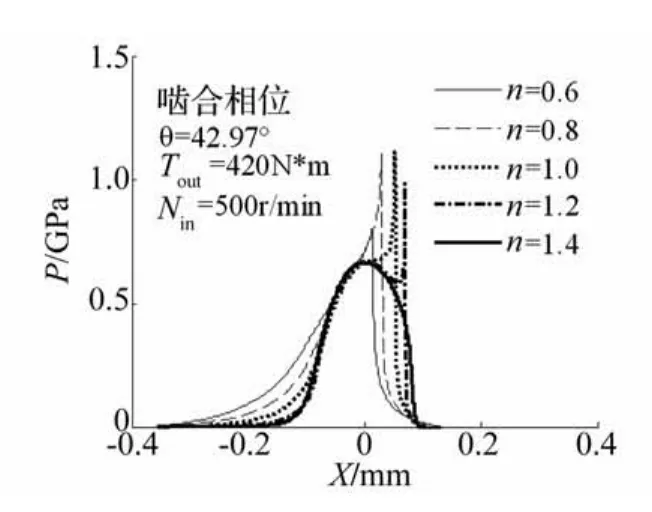
图12 流变指数n对油膜压力的影响Fig.12 Pressure distribution for different n
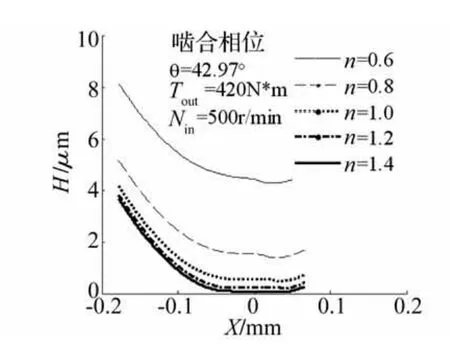
图13 流变指数n对膜厚的影响Fig.13 Film shape for different n
3.3 短幅系数k1对润滑的影响
图14~15给出了短幅系数k1对摆线轮平均半径处润滑性能的变化规律。随着短幅系数k1增加,在大部分啮合区间范围内压力增加,承载能力下降,膜厚减小。表明在满足设计要求情况下,短幅系数k1减小,有利于提高润滑性能。
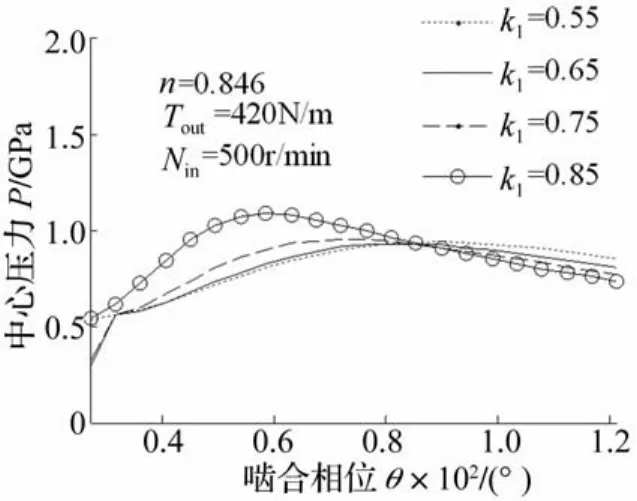
图14 中心压力随短幅系数k1变化Fig.14 The variation of center-pressure for different k1
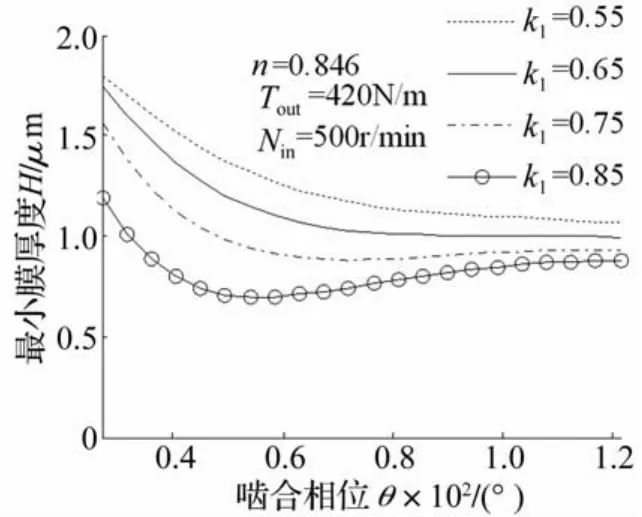
图15 最小膜厚随着短幅系数k1变化Fig.15 The variation of min-film thickness for different k1
4 结 论
论文基于Ostwald模型对摆线针轮线接触脂润滑弹流问题进行研究,得出啮合过程中最小膜厚值,并与经验公式对比,验证数学模型的正确性。以摆线轮θ=arccos K1处润滑状态作为判断依据,研究载荷、转速和流变指数对摆线针轮传动滑状态的影响规律,表明随着转速提高,二次压力峰高度降低并向入口区移动,膜厚相应增加,润滑膜平行部分缩短;而随着载荷增加,接触区变宽,二次压力峰增加,其位置向出口区移动,膜厚略微减小,膜厚颈缩现象更加明显;随着流变指数n变化,当n<1时,随着流变指数n增加,二次压力峰增加,并向出口区移动,膜厚相应降低;当n>1时,随着流变指数n增加,二次压力峰减小并向出口区移动,最后二次压力峰消失,接近Hertz压力,膜厚相应减小。讨论了短幅系数k1对润滑的影响,随着短幅系数k1增加,在大部分啮合区间范围内压力增加,承载能力下降,膜厚减小。在满足设计要求情况下,短幅系数k1减小,有利于提高润滑性能。
[1]朱才朝,陈爽,马飞,等.轮齿修形对兆瓦级风电齿轮箱动态特性影响[J].振动与冲击,2013,32(7):123-128.
ZHU Cai-chao,CHEN Shuang,MA Fei,et al.Effect of gear teeth modification on dynamic characteristics of a megawatt level wind turbine gearbox[J].Journal of Vibration and Shock,2013,32(7):123-128.
[2]Liu H J,Mao K,Zhu C C,et al.Mixed lubricated line contact analysis for spur gears using a deterministic model[J].ASME Journal of Tribology,2012,134:021505-1-7.
[3]Liu H J,Mao K,Zhu C C,et al.Parametric studies of spur gear lubrication performance considering dynamic loads[J].Proc.IMechE,PartJ:Journal of Engineering Tribology,2012,226(9):731-737.
[4]Zhu D,Wang J X,Ren N,et al.Mixed Elastohydrodynamic lubrication in finite roller contacts involving realistic geometry and surface roughness[J].ASME,Journal of Tribology,2012,134:011504-1-10.
[5]Chu L M,Lin J R,Li W L,et al.Model for line contact EHL problems consideration of effects of navierSlip and lubricant rheology[J].ASME,Journal of Tribology,2012,134:031502 -1-8.
[6]Yang P,Yang P R.Analysis on the thermal elastohydrodynamic lubrication of tapered rollers in opposite orientation [J].Tribology International,2007,40:1627-1637.
[7]Liu X L,Yang P R.Analysis of the themal elastohydrodyanamic lubrication of a finite line contact[J].Tribology International,2002,35:137-144.
[8]Zhu C C,Liu M Y,Liu,H J,et al.A thermal finite line contact EHL model of a helical gear pair[J].Proc IMechE Part J:J Engineering Tribology,2013,227(4)299-309.
[9]刘晓玲,杨沛然.指数率流体热弹流润滑分析[J].润滑与密封,2007(8):19-23.
LIU Xiao-lin,YANG Pei-ran.Analysis of power law fluid thermal elastohydrodynamic lubrication[J].Lubrication engineering,2007(8):19-23.
[10]于玫,黄平.线接触脂润滑热弹性流体动力润滑数值分析[J].轴承,2011(1):8-12
YU Mei,HUANG Ping.Numerical analysis on thermal elastohydrodynamic grease lubrication in line contacts[J].Bearing,2011(1):8-12.
[11]李媛,刘小君,王静,等.脂润滑条件下微凹坑表面的摩擦特性研究[J].合肥工业大学学报(自然科学版),2012,35 (11)1444-1446.
LI Yuan,LIU Xiao-jun,WANG Jing,et al.Ivestigation of tribological properties of concave surfaces under grease lurication[J].Journal of Hefei University of Technology,2012,35 (11)1444-1446.
[12]白新瑞,刘晓玲.乏油条件下圆柱滚子轴承的弹流润滑分析[J].润滑与密封,2013,38(1)45-50.
BAI Xin-rui,LIU Xiao-ling.Analysis of elastohydrodynamic lubrication for cylindrical roller bearings under starved oilsupply condition[J].Lubrication Engineering,2013,38(1)45 -50.
[13]Yang P,Wen S.A generalized reynolds equation for non-Newtonian thermal elastohydrodynamic lubrication[J].ASME Journal of Tribology,1990,112(10):631-636.
[14]Mihailidis A,Agouridas K,Panagiontidis K.Non-newtonian starved thermal-elastohydrodynamic lubrication of finite line contact[J].Tribology Transactions,2013,56:88-100.
[15]Yang Peiran,Wen Shizhu.A generalized Reynolds equation based on non-newtonian flow in lubrication mechanics[J].Acta Mechanica Sinica,1991,3(5):283-289.
[16]Venner C H,Ten Napel W E,Bosma R.Advanced multilevel solution of the EHL line contact problem[J].ASME Journal of Tribology,1993,112(7):426-431.
Numerical analysis of elastohydrodynamic lubrication for cycloid drives
SUN Zhang-dong,ZHU Cai-chao,LIU Huai-ju,LIU Ming-yong,GU Zong-lin
(The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400030,China)
Numerical analysis of grease elastohydrodynamic lubrication for cycloid drives was performed.The minimum film thickness of meshing process was obtained.Comparting it with that obtained from an empirical formula,the correctness of model was verified.The average radius of cycloid wheel's lubrication state was taken as the judgment basis,the effects of rotating speed,load and rheological index on grease EHL were analyzed.Results showed that with increase in rotating speed,the second pressure peak drops and moves toward the inlet,the film thickness increases;with increase in load,the contact field width increases,the second pressure peak rises and moves toward the out let,the film thickness decreases slightly;with increase in the rhoological index n,the second pressure peak firstly increases and then decreases,finally approaches Hertz pressure,and it moves toward the outlet,the film thickness decreases.The effect of the short ampliitude coefficient k1on lubrication was discussed,it was shown that under the conditions to meet design requirements;the decrease in k1can improve the lubrication performance.
Cycloid Drive;Grease Lubrication;Numerical Analysis;Ostwald
TH117
A
10.13465/j.cnki.jvs.2014.23.035
由国家自然科学基金(51175523);教育部博士点基金(20110191110039)资助
2013-07-08 修改稿收到日期:2013-12-12
孙章栋男,博士生
朱才朝男,博士,教授,博士生导师,1967年生
