基于经验模式分解和主元分析的滚动轴承故障诊断方法研究
2014-05-16徐卓飞张海燕张明龙吴欣阳
徐卓飞,刘 凯,张海燕,王 丹,张明龙,吴欣阳
(1.西安理工大学机械与精密仪器工程学院,西安 710048;2.西安理工大学印刷包装工程学院,西安 710048)
基于经验模式分解和主元分析的滚动轴承故障诊断方法研究
徐卓飞1,刘 凯1,张海燕2,王 丹1,张明龙2,吴欣阳2
(1.西安理工大学机械与精密仪器工程学院,西安 710048;2.西安理工大学印刷包装工程学院,西安 710048)
提出了一种融合经验模式分解和多元统计的轴承故障诊断新方法,主要包括基于信号Hilbert-Huang变换的特征提取和对故障特征集的主成分分析:首先运用EMD将振动信号分解成不同特征时间尺度的单分量固有模态函数,采取Hilbert-Huang变换获取分解信号的瞬时频率,计算基本模式分量与瞬时频率的统计特征集;之后对统计特征集进行主成分分析,大幅降低特征向量的维数,获取主元特征集;最后利用支持向量机,完成了对于滚动轴承常见三类故障的分类,并分析了振动信号时域频域的统计特征值与故障模式之间的联系。
滚动轴承;故障诊断;经验模态分解;主成分分析;统计特征
滚动轴承是旋转机械的核心部件,其状态对设备的运行起着重要作用。轴承一旦出现故障,会产生连锁反应,对设备产生严重损坏甚至造成事故,因此与轴承相关的故障诊断技术,一直是机械故障诊断研究的重要内容[1-4]。振动信号分析是轴承故障诊断中最常用、最有效的方法,但是其相关研究中存在着如下难点:①轴承故障的振动信号多是非平稳、非线性的,因此以傅里叶变换为理论依据的传统的信号处理和特征提取方法很难得到较好的分析效果[5-6];②在故障模式分类的过程中,往往涉及大量相关故障特征,如何评价特征值的有效性、降低计算的复杂度、合理的选取故障特征集等问题,对于最终的故障诊断效果起着决定性作用[7-8]。
为了解决上述两个难点问题,提出了融合经验模态分解(Empirical Mode Decomposition,EMD)和主成分分析(Principal Component Analysis,PCA)的滚动轴承故障诊断方法,以发挥其各自在故障识别中的优势:经验模态分解适用于非线性和非平稳信号序列处理,可以有效进行轴承故障的振动信号分析;主元分析则可有效去除冗余信息并降低特征向量维数,提高识别的效率,保留主要特征的完整性[9-11],同时,根据主元特性还可以发掘统计特征和故障模式之间的实际联系,最终实现滚动轴承故障模式的分类。
1 基于EMD的统计特征提取
EMD是一种具有自适应性的时频分析方法,可根据信号的局部时变特征进行自适应的时频分解,将信号分解成若干个本征模式分量函数(Intrinsic Mode Function,IMF),每个分量表现出单一性并反映信号中的一种特有频率信息。EMD在本质上对信号进行平稳化处理,将信号中不同尺度的波动或趋势逐级分解开来,主要过程如下[9]:
①确定信号x(t)的局部极大值序列和局部极小值序列,分别记为xmax和xmin;②依据xmax和xmin确定信号x(t)的上、下包络谱以及局部均值m(t)=(xmax+xmin)/2;③信号与局部均值的差记为h1(t)=x(t)-m(t),若h1(t)符合IMF条件[9],则将其作为x(t)的第一个IMF分量,若不满足条件,则使x(t)=h1(t),重复上述步骤n次,直至得到第一个基本模式分量c1(t);④分解出第一个基本模式分量后,从x(t)中减去c1(t),得到剩余值序列r1(t)=x(t)-c1(t),重复上述步骤,依次继续获得第二个、第三个等基本模式分量,依次记为c2(t)、c3(t)等,最后原始信号剩余的部分为rn(t),则有:

式(1)中,ci(t)为EMD分解得到的各个IMF;rn(t)为信号分解后的余项,i和n为分解次数。突出信号的高频振动序列,有利于故障特征提取的有效性。信号的高频部分集中在前几个主要IMF分量中,故将其留下进行后续特征提取;而对于最后的几个IMF残余分量则需要去除,这是因为残余分量以低频噪声干扰为主。对分解得到的各个分量组按照式(2)进行Hilbert变换,并按照式(3)构造解析信号[12]

通过信号分解,得到主要本征模式分量和其对应的瞬时频率。主要模式分量中包含了高频信息,经过HHT变换后得到的时频谱具有一定的物理意义,研究选取主要本征模式分量及其相应瞬时频率的统计特征值作为信号的原始故障特征集,详见第三部分实验。
EMD分解虽能有效地分析和处理信号,但由于其采用了三次样条曲线进行差值,使得信号端点处极值点的不确定,信号两端往往会产生发散现象,随着分解过程的逐步进行,这种发散会逐渐向内“污染”整个信号序列,进而使分解结果失真并失去实际物理意义,产生模态混叠的现象,这就是所谓EMD的端点效应,这种现象对于较短的、低频的信号序列影响尤为明显,为了减少端点效应对于研究结果的影响[9,13],研究采取了选取较长信号进行EMD变换,之后将各个IMF分量的两端信号进行截取,以减少端点效应影响。
2 故障特征的主元分析
主成分分析是多元统计分析中常用的多维数据分析方法,它与时域、频域分析方法有着本质差别,其特点是能同时处理多维或多变量的数据,从这些数据中解释隐含的统计信息特征,特别在消除数据相关性方面非常有效。对于轴承故障诊断中获取的多维特征集,需有效地简化信息以提高其计算效率,因此在HHT得到特征集的基础上进行了PCA分析[14]。
PCA广泛应用于化工、地学等领域,它通过降维技术把多个变量化为少数几个主成分,这些主成分能够反映原始变量的大部分信息,通常表示原始变量的线性组合

式中X中每一行对应一个样本(即一组特征值),每一列对应一个特征变量,将样本的协方差矩阵S作为总体协方差矩阵的估计,可依据式(7)从S出发求解主成分,式(7)中,向量xi表示X中一个样本的全部特征值,即xi=(xi1,xi2,…,xip)′表示第i个样本中的所有p个特征值,为样本均值

设λ1,λ2,…,λp为S的p个特征值,T=t1,t2,…,tp为相应正交单位特征向量,则∑ti=λiti,t′iti=1,t′itj=0,其中i≠j;i,j=1,2,…,p,若记Λ是对角线为λ1,λ2,…,λp的对角阵

考虑到如下线性变换

式中A为单位向量矩阵,Y=[y1,y2,…,yn]为主元特征集。考虑y1的方差

式(11)表示第i主元的贡献率,式(12)表示前m主元的累积贡献率。提取后的得到主元特征集Y:Y=[y1y2y3… yn],n为选取的主成分个数,使n的个数大幅小与p,即实现特征集的降维。
3 滚动轴承故障分类
3.1 实验说明
本研究的实验数据全部来自美国Case Western Reserve University电气工程实验室[15]。实验中测试的轴承是由SFK公司生产的6205-2RS深沟球轴承,轴承和实验参数列于表1中。对实验中轴承进行电火花加工,以模拟点蚀故障,故障点分别在外圈、内圈及滚动体上,点蚀的直径包括0.178 mm、0.356 mm、0.533 mm三种。

表1 实验参数Tab.1 Experimental parameters

图1 实验装置Fig.1 Experimental apparatus
图1是实验装置,滚动轴承被安装在马达驱动的机械系统上,将振动加速度传感器垂直固定在感应电机驱动端支撑轴承上方的机壳上,分别采集滚动轴承在正常、内圈故障、外圈故障以及滚动体故障下的原始振动信号,采样频率为12 kHz。
选取六个样本集,样本A、B、C包括不同损伤程度下的三种故障状态,样本D、E、F分别代表不同故障程度的内圈故障、外圈故障和滚动体故障,具体如表2所示。以长度1 024个采样点的数据为一个样本,为抑制端点效应,先将样本长度设置为2 048,经EMD分解及Hilbert变换之后,将各分量两端信号截掉,余下中间原始信号的1 024个采样点,已达到抑制端点效应的目的。
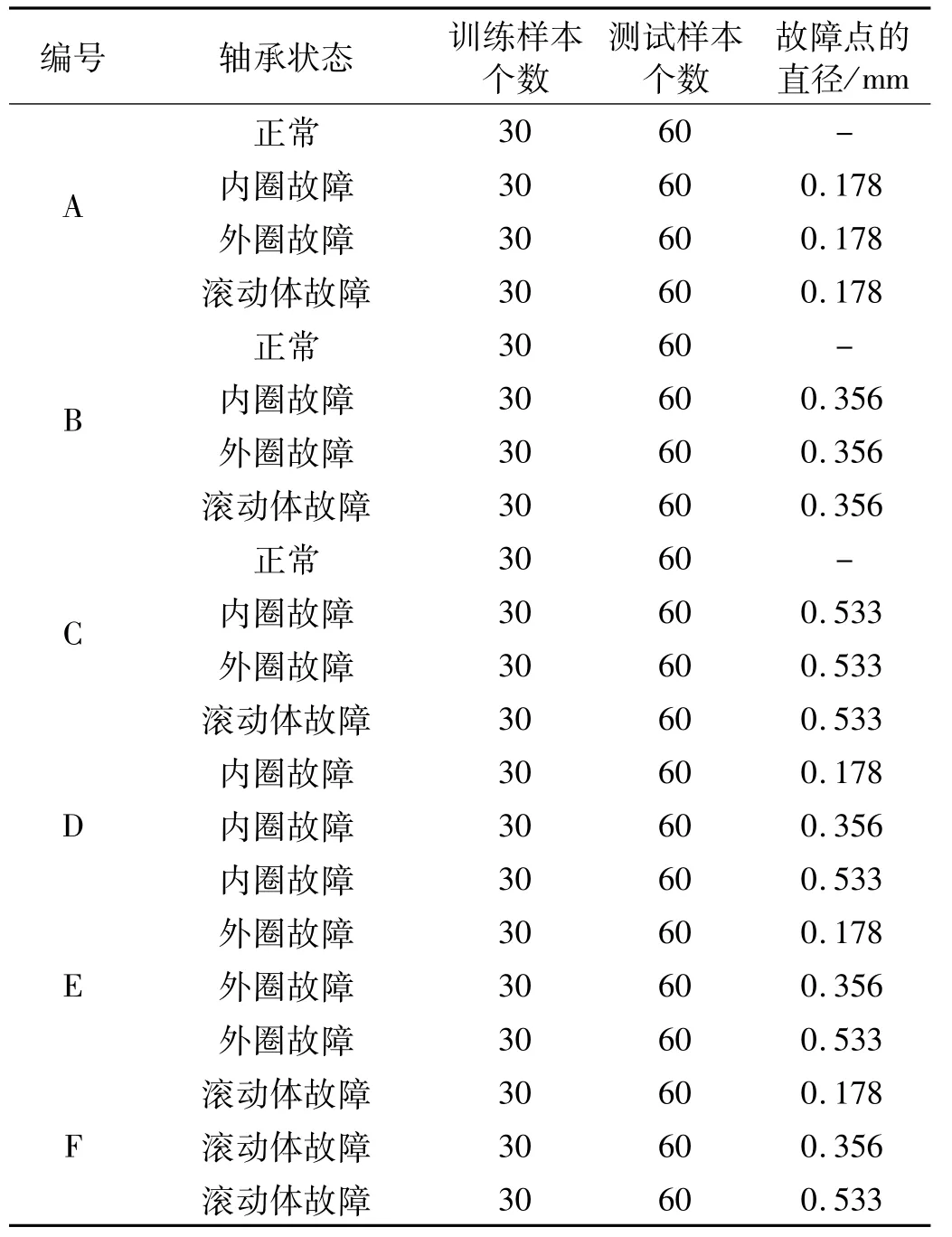
表2 轴承故障样本Tab.2 Test sample
3.2 诊断模型
研究融合上述EMD与HHT特征提取和多元分析方法,建立轴承故障诊断模型,如图2所示,按照诊断模型进行故障分类研究,其中按照累积贡献率分布情况,选择适当的主元特征作为输入向量,将对应的滚动轴承故障模式作为输出向量,利用支持向量机(Support Vector Machine,SVM)等模式分类方法,最终实现滚动轴承处于不同故障种类和不同损坏程度下的故障分类研究。
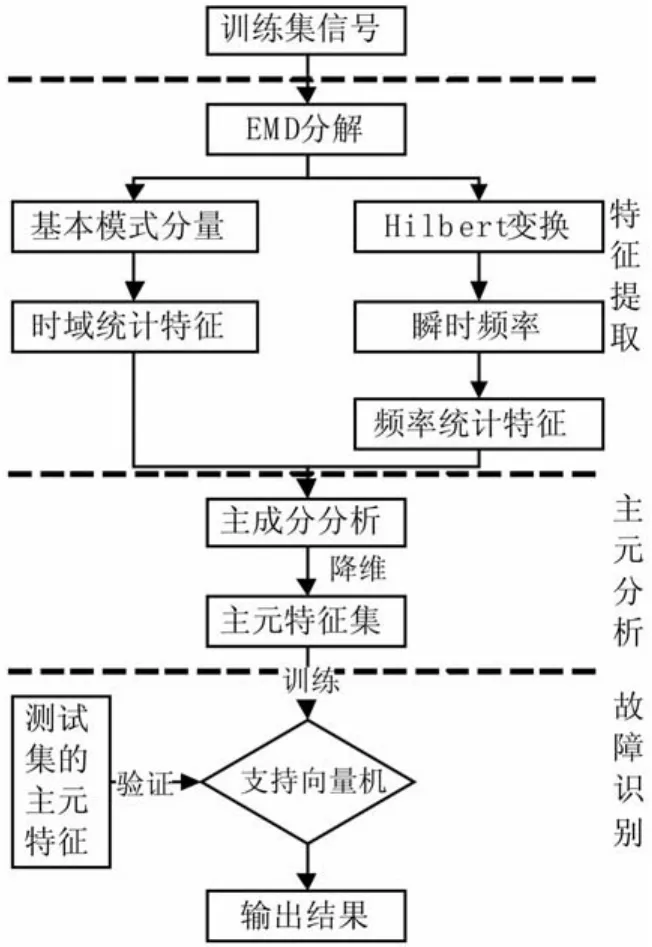
图2 基于EMD与PCA的故障诊断模型Fig.2 Fault diagnosis model based on EMD and PCA
3.3 特征提取与PCA分析
图3中表示了轴承内圈故障信号经过经验模式分解后的IMF分量,c1(t)-c5(t)包含主要的高频分量,本次研究选取这5个分量为特征集来源,剩余分量中包含了低频信息。图3(a)中的分解结果未对端点效应进行抑制,图3(b)按照3.1节描述方法对信号进行了处理以抑制端点效应,对比二者可发现:高频分量中,图3(b)中IMF1-4两端处的发散现象对比图3(a)得到了抑制,左端更为明显;图3(b)中低频分量IMF5体现出了明显的周期性,而图3(a)中IMF5发生了严重的失真,已不具备明显的周期性。可见,在故障特征计算之前,有必要对端点效应进行抑制,以保证其有效性和真实性。
故本次研究选取IMF1-5分量,并进行Hilbert变换,这样对每一个样本而言,有10个分量,包括5个IMF分量和5个相应的瞬时频率序列,再分别计算其相应的8个统计特征值,依次是均值、平方和、标准差、峰值、极差、变异系数、偏度和峰度,即从每一个样本中提取出一个80维特征向量。其中,变异系数是衡量数据资料中各变量观测值变异程度的一个统计量;偏度则反映了总体分布密度曲线的对称性信息,偏度越接近于0,说明分布越对称,否则分布越偏斜;峰度反映了总体分布函数密度曲线在其峰值附近的陡峭程度,所选特征具体计算如表3所示。

表4 样本C的累积贡献率Tab.4 Cumulative contribution rate

图3 轴承内圈故障信号的EMD分解结果Fig.3 EMD decomposition result for the signal of inner fault

表3 所选取特征Tab.3 Selected characteristic values

图4 各主成分的累积贡献率Fig.4 Cumulative contribution rate of principal component vector
对C中训练集进行特征提取,可得到相应的特征矩阵X,其规格为120×80,120行代表正常、内圈故障、外圈故障、滚动体故障的所有样本,80列代表了每一个样本的特征向量。之后对特征矩阵进行标准化,按照(7)-(12)对其进行主成分分析,其累积贡献率如图4和表4所示,可以看到仅第1个主元的累积贡献率已达到98%以上,前2个主元达到99%以上,从累积贡献率来看,PCA有效地实现了特征向量降维,可根据累积贡献率变化选取不同个数的主元作为新的特征集,进行后续分类比较。
3.4 故障模式识别
在完成故障特征的分析之后,选择不同的主元个数以进行故障识别研究,在决策时需要相应分类算法,考虑到SVM具有很好的泛化能力,对解决小样本模式分类问题有独特的优势,所以在故障识别时选用它来检验主元特征向量对故障分类的决策能力[16-17]。对表2中的故障样本A-F进行分类决策研究,分别选取主元个数为1-4,并对每组未经PCA分析的80维原始特征向量进行分析,对比研究PCA对于特征集识别效果的影响。

图5 散点得分图(1-4分别代表正常、内圈故障、外圈故障和滚子故障)Fig.5 Scatter score plot
图5是C数据集中前两个主成分对于训练集的得分图,可以看出训练集的四类轴承状态仅依靠前两个分量就得到了较好的分类,证明了所提出方法的有效性和正确性。
对四组样本进行分类研究,利用SVM网络进行训练,并对验证集进行验证,分类准确率记录在表5中,其中包括对训练集识别的正确率和未知样本验证集的识别率。
A-C组数据是故障的类型识别问题,可以发现,随着主元个数的增加,识别率逐步提高,当主元个数为4时,其累积贡献率达到99.99%,A与C的识别率也都接近98%;未经PCA分析的特征集都实现了接近100%识别率,而经过PCA提取主元后,识别率会有所下降,这是由于在消除冗余信息时也在一定程度上损失了关键信息造成,但是经过维数压缩的特征集仍保持了较高的识别率。
D-F组数据是故障程度分类问题,经SVM训练分类后都可以达到几乎100%的正确识别率;经PCA分析后,识别率下降程度较高,以选取主元个数为2为例,内圈故障的识别率可保持在90%左右,而滚动体故障与外圈故障识别效果仅为70%左右,说明所提出特征集对于故障程度识别可取得较好效果,但是经过PCA分析后,滚动体故障与外圈故障识别率下降较高,内圈识别基本满足要求。
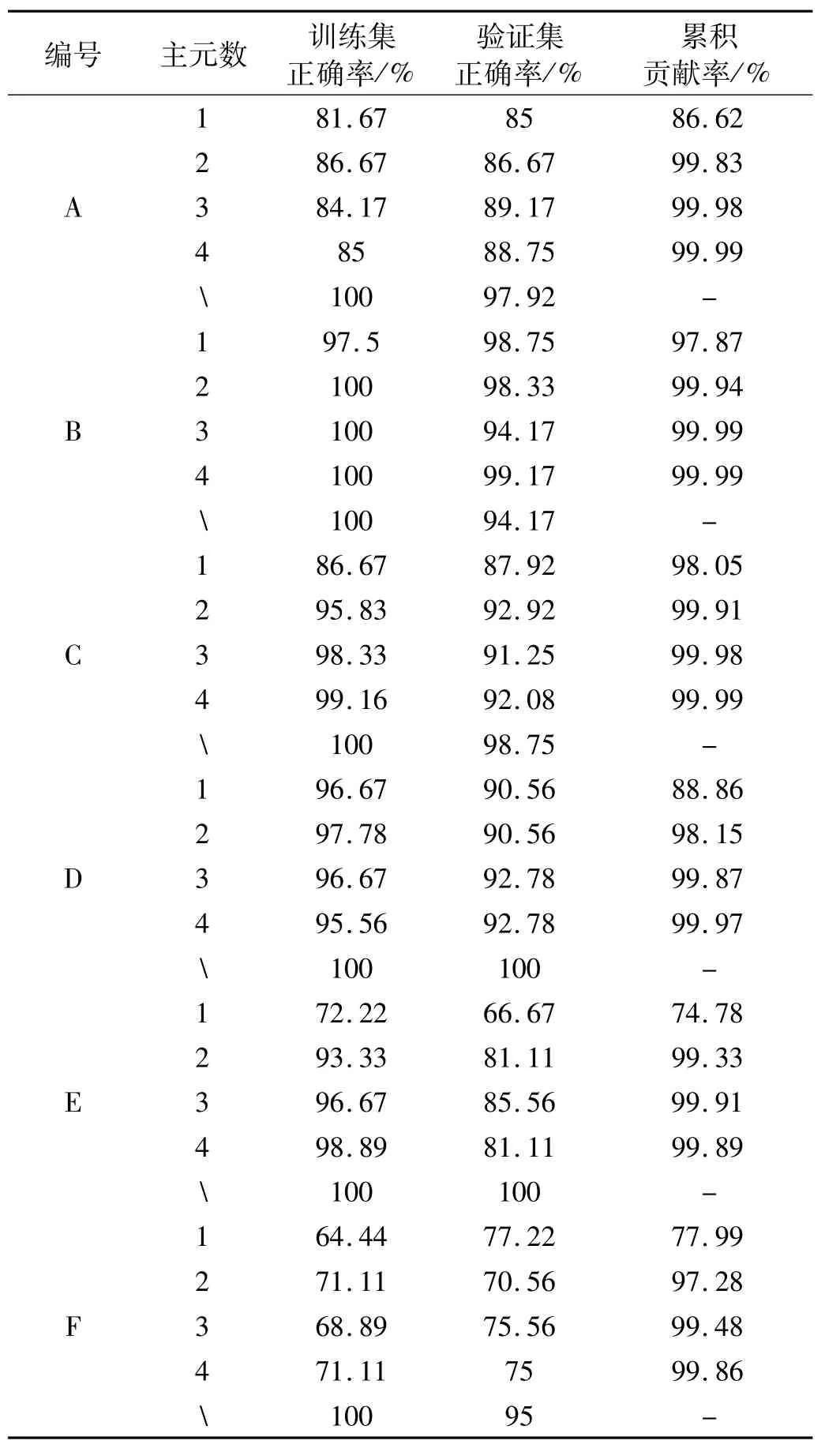
表5 滚动轴承故障分类结果Tab.5 Fault classifications results of rolling bearings
综合故障种类识别和故障程度识别的结果:发现本文提出的基于EMD与HHT的统计特征集可较好地区分轴承故障类型和故障程度;经PCA分析后,数据维数会得到有效降低,大大压缩了原始特征集,提高了识别运算效率,而且仅依靠少数1-4个主元特征便可有效地识别故障种类,并依然保持较高的准确率;但是PCA的使用在另一方面会造成部分信息的遗漏,与原始特征集相比,在一定程度上降低识别效果,这种负面作用对于故障种类识别影响较小,可以接受,但对于故障程度识别影响较大。
3.5 主元特征分析
主成分分析在有效降低原始特征集维数的同时,很好地解释了各个原始特征集对于故障模式的相关性,图6以样本C为例,绘制出前7个主元特征系数的分布图,特征系数的分布,表征了各个原始参数在主元中的权重。
依式(9)可得到各个主元向量Y与统计征集X的关系,将每一个原始80维特征集与主成分系数矩阵T相乘,得到的就是其相应的主元Y

式中T是一个80维系数矩阵,其计算参见式(10),数值的大小表示了对应原始特征在主元中所占的权重,系数值越大,说明相应编号的原始特征对于该主成分的贡献越大。

图6 主元系数分布图Fig.6 Coefficient distribution of the principal component vector
观察图6中的系数分布情况,可以发现第1-5主元都是由80个原始特征组成,但只有少数几个特征值值所占比重较高,多数特征的系数接近于0,数量级很小,可以看出PCA分析可以有效地提取出更为敏感的少数特征,并构成新的特征集,反向追溯每个主元的构成,可以推测出其实际物理意义。
第1-5主成分中,系数编号48、56、64、72占有比例最大,其分别对应IMF1-5瞬时频率的偏度值,因此认为这5个主成分是各个IMF分量的偏度值按不同权重相加组合的量;第6-7主成分中,系数编号5、13、21占据主导地位,对应IMF1-3的极差,可见这2个主成分主要表示高频分量时域极差的状态。
针对本次研究提取的故障特征集可以看出,瞬时频率的偏度对于故障识别贡献最大,而在选取少数主元的同时,时域信息发生了遗漏,如6-7主元的时域极差就被遗漏,这是PCA的负面效应,但是少数主元依然可以保证较高的识别率,并且有效地简化特征集的复杂度,还可通过主成分系数找到与故障模式相关性最高的实际物理量。
4 结 论
本研究以滚动轴承的故障分类为目标,重点针对振动信号的非平稳性特点,采用了基于EMD与HHT的特征提取方法,在特征集的进一步分析与提取中进行了PCA分析以获取主元特征,主要结论如下:
(1)通过经验模式分解和HHT变换,获得了各个IMF分量的时域和瞬时频率的故障特征集,较好的提取了信号的高频分量,有效去除了低频分量噪声的干扰,对不同故障模式、不同故障程度的轴承数据进行了验证,实现了较高的故障识别率,认为所提出故障特征集对于滚动轴承故障有着较好的识别效果;
(2)通过PCA分析原始特征集,可以大幅压缩特征向量的维数,去除冗余信息以简化故障模式识别中的计算复杂度,实现了用极少数主成分替代维数较高的原始特征集,经研究发现PCA分析虽然会略微降低识别率,但对于轴承故障分类依然有着较好的效果,实现了维数的有效降低,通过实验发现,当累计贡献率较高时,训练集与验证集的识别率普遍偏高,认为较高累积贡献率可更好地保证故障特征集的完整性。
研究所提出方法也存在不足之处,主要发现PCA对于故障程度的识别率会有一定的负面影响,这是由于选取少数主元造成信息丢失所致,如何进一步提高识别率、选择更为敏感的特征集将是后续研究主要内容。
[1]Tsao W C,Li Y F,Le D D,et al.An insight concept to select appropriate IMFs for envelope analysis of bearing fault diagnosis[J].Measurement,2012,45(6):1489-1498.
[2]吴强,孔凡让,何清波,等.基于小波变换和ICA的滚动轴承早期故障诊断[J].中国机械工程,2012,23(7):835-840.
WU Qiang,KONG Fan-rang,HE Qing-bo,et al.Early fault diagnosis ofrollingelementbearingsbasedonwavelet transform and independent component analysis[J].China Mechanical Engineering,2012,23(7):835-840.
[3]Jena D P,Panigrahi S N.Bearing and gear fault diagnosis using adaptive wavelet transform of vibration signals[J].Procedia Engineering,2012,50:265-274.
[4]周智,朱永生,张优云,等.基于EEMD和共振解调的滚动轴承自适应故障诊断[J].振动与冲击,2013,32(2):77-80.
ZHOU Zhi,ZHU Yong-sheng,ZHANG You-yun,et al.Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J].Journal of Vibration and Shock,2013,32(2):77-80.
[5]李辉,郑海起,杨绍普.基于EMD和Teager能量算子的轴承故障诊断研究[J].振动与冲击,2008,27(10):15 -18.
LI Hui,ZHENG Hai-qi,YANG Shao-pu.Bearing fault diagnosis based on EMD and teager kaiser energy operator [J].Journal of Vibration and Shock,2008,27(10):15 -18.
[6]康守强,王玉静,杨广学,等.基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法[J].中国电机工程学报,2011,31(14):96-102.
KANG Shou-qiang,WANG Yu-jing,YANG Guang-xue,et al.Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass support vector machine[J].Proceedings of the CSEE,2011,31(14):96-102.
[7]王冬云,张文志.基于小波包变换的滚动轴承故障诊断[J].中国机械工程,2012,23(3):295-298.
WANG Dong-yun,ZHANG Wen-zhi.Fault diagnosis study of ball bearing based on wavelet packet transform[J].China Mechanical Engineering,2012,23(3):295-298.
[8]雷亚国,何正嘉,訾艳阳.基于混合智能新模型的故障诊断[J].机械工程学报,2008,44(7):112-117.
LEI Ya-guo,HE Zheng-jia,ZI Yan-yang.Fault diagnosis based on novel hybrid intelligent model[J].Chinese Journal of Mechanical Engineering,2008,44(7):112-117.
[9]Huang N E,Shen Z,Long S R.The Emprical model decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Society,Lond,1998,454(A):903-995.
[10]赵立杰,柴天佑,王纲.多元统计性能监视和故障诊断技术研究发展[J].信息与控制,2004,33(2):197-200.
ZHAO Li-jie,CHAI Tian-you,WANG Gang.The progress of multivariatestatisticalperformancemonitoringandfault diagnosis[J].Information and Control,2004,33(2):197 -200.
[11]Detroja K P,Gudi R D,Patwardhan S C.Data reduction algorithm based on principle of distributional equivalence for fault diagnosis[J].Control Engineering Practice,2012,20 (10):1033-1041.
[12]何清波,冯志华,孔凡让.设备噪声监测中主分量的特征表示[J].光学精密工程,2006,14(6):1093-1099.
HE Qing-bo,FENG Zhi-hua,KONG Fan-rang.Principle component representations for machine noise monitoring[J].Optics and Precision Engineering,2006,14(6):1093 -1099.
[13]Huang N E.Computer implicated empirical mode decomposition method.Apparatus,and article of manufacture[P].U.S.Patent.1996.
[14]李常有,徐敏强,郭耸.基于改进的Hilbert-Huang变换的滚动轴承故障诊断[J].振动与冲击,2007,26(4):39 -41.
LI Chang-you,XU Ming-qiang,GUO Song.A fault diagnosis qpproach to rolling element bearings based on improved Hilbert-Huang transformation and linear neural network[J].Journal of Vibration and Shock,2007,26(4):39-41.
[15]Loparo KA.Bearings vibration data set,Case Western Reserve University.http://www.eecs.cwru.edu/laboratory/Bearing/download.htm.
[16]洪杰,韩磊,苗学问,等.基于支持向量机的滚动轴承状态寿命评估[J].北京航空航天大学学报,2010,36(8):897-899.
HONG Jie,HAN Lei,MIAO Xue-wen,et al.Assessment based on support vector machine for rolling bearing grade-life [J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(8):897-899.
[17]刘永斌,何清波,孔凡让,等.基于PCA和SVM的内燃机故障诊断[J].振动、测试与诊断,2012,32(2):250 -255.
LIU Yong-bin,HE Qing-bo,KONG Fan-rang,et al.Fault diagnosis based on PCA and SVM for internal combustion engine[J].Journal of Vibration,Measurement and Diagnosis,2012,32(2):250-255.
A fault diagnosis method for rolling bearings based on empirical mode decomposition and principal component analysis
XU Zhuo-fei1,LIU Kai1,ZHANG Hai-yan2,WANG Dan1,ZHANG Ming-long2,WU Xin-yang2
(1.School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an 710048,China;2.School of Printing and Packaging Engineering,Xi'an University of Technology,Xi'an 710048,China)
A new fault diagnosis method for rolling bearings based on empirical mode decomposition(EMD)and multivariate statistics was proposed.Hilbert-Huang transformation and principal component analysis(PCA)were used in this method.A vibration signal was decomposed into the basic mode components with EMD and the instantaneous frequency of each component was obtained with Hilbert-Huang transformation.Then,the statistical characteristics of the instantaneous frequency and the basic mode components were calculated.The statistical characteristics were analyzed with PCA in order to reduce the number of dimensions of the feature vector and get the principal component characteristics.Finally,the classification of three failure modes in rolling bearings was completed and the relationship between the statistical characteristics and failure modes was obtained.
rolling bearing;fault diagnosis;EMD;PCA;statistical characteristics
TH117;TP183
A
10.13465/j.cnki.jvs.2014.23.024
国家自然科学基金项目(51275406,51305340);陕西省自然科学基础研究计划项目(2013JM7009);陕西省教育厅科学研究计划项目(2013JK1030)
2013-04-16 修改稿收到日期:2013-12-19
徐卓飞男,博士生,1985年生
刘凯男,教授,博士生导师
邮箱:kliu@mail.xaut.edu.cn
