次分数布朗运动下带交易费用的备兑权证定价

肖炜麟，张卫国，徐维军

（1.浙江大学管理学院，浙江杭州 310058；2.华南理工大学工商管理学院，广东广州 510640）

值得指出的是Γ=∂2V/∂S2，称为保值因子。对于备兑权证的多头而言，到期日的收益为凸函数，因此有Γ＞0，从而对于支付任意比例交易费的看涨或看跌备兑权证，由Black-Scholes公式得到的价值与本文模型得出的价格比较，差别仅在于波动率，即：

次分数布朗运动下带交易费用的备兑权证定价

肖炜麟1，张卫国2，徐维军2

（1.浙江大学管理学院，浙江杭州 310058；2.华南理工大学工商管理学院，广东广州 510640）

为了体现金融资产的长记忆性，采用次分数布朗运动刻画备兑权证标的资产价格变化的行为模式。利用随机分析理论和偏微分方程方法，建立了次分数布朗运动下带交易费用的备兑权证定价模型，进一步研究了定价模型的参数估计问题。最后，采用我国权证市场实际数据进行了实证分析，通过比较不同定价模型的结果说明了长记忆性和交易费用对定价结果有着显著的影响。

次分数布朗；交易费用；备兑权证；偏微分方程；二次变差

1 引言

备兑权证是由标的资产发行人以外的第三方发行的权证，并规定持有人有权利而非义务在合约规定的某一特定时间买入（卖出）标的资产。由于权证产品的灵活性，且权证的“T+0”交易等特点使其成为短线投资者首选产品。尽管备兑权证本质上类同于欧式期权，但由于备兑权证具有杠杆效应和套期保值作用，使得备兑权证成为我国金融衍生产品的重要组成部分。

基于传统的有效市场和几何布朗运动的假设，在Black-Scholes理论框架下，备兑权证的定价问题在国内外得到了大量研究［1-2］。然而Black-Scholes模型中假设市场交易中没有交易费用，而现实中每次股票交易，都需要交纳手续费、印花税。而且历史上印花税的每次调整都会引起股市的一次振荡。因而交易费用对于金融市场的影响是显著的。为了更好地反映现实交易情况，Leland［3］首次提出了带交易费用的欧式期权定价模型，但该模型仅能运用到香草期权等一些特殊期权的定价。此后，大量学者在几何布朗运动的假设下，研究了带交易费用的期权定价问题［4-5］。然而，近年来对金融资产收益率的实证研究表明：金融资产价格之间并非随机游走，而呈现不同程度的长期相关性，并且资产收益率的分布也不是服从正态分布，而是具有“尖峰厚尾”等特性。Peters［6］于1989年提出了分形市场假说，应用R/S法分析了不同资本市场（如股票市场和汇率市场），都发现了分形结构和非周期循环的存在。由于分形市场的特征指数及尺度参数能够很好地刻画金融市场波动性及资产收益率的“尖峰厚尾”分布等，因此，众多学者研究了分数布朗运动下期权定价问题［7-10］和我国权证的定价问题［10-12］。

由于分数布朗运动不是半鞅，故无法采用已有的随机积分理论对其进行分析。尽管众多学者针对分数布朗运动定义了不同的随机积分［13-14］，但是将分数布朗运动应用到金融市场会产生套利机会［15］或者自融资策略不符合经济学理论［16］。从而，大量学者采用了修正的分数布朗运动来刻画金融资产价格变化的行为模式，如次分式布朗运动［17-18］。由于，次分式布朗运动是一种比分数布朗运动更为普遍的高斯过程，它不仅具有自相似性和长记忆性等分数布朗运动具有的性质，而且可将其应用于金融［19］。Yan Litan等［20］给出了次分数布朗运动的随机积分，并指出次分数布朗运动可以用来刻画金融资产的随机波动性。

为了刻画金融资产的长记忆性，同时为了考虑交易费用，本文在次分式布朗运动环境下，研究了带交易费用的备兑权证定价问题。通过引入关于次分数布朗运动的随机积分和偏微分方程技术，得到了备兑权证的定价模型。进一步，为了将模型应用于实践，本文研究了定价模型的参数估计问题。最后，结合我国权证市场现实情况，给出了实证分析，比较了不同定价模型的定价结果，说明了次分数布朗运动下带交易费用定价模型的合理性。

2 定价模型

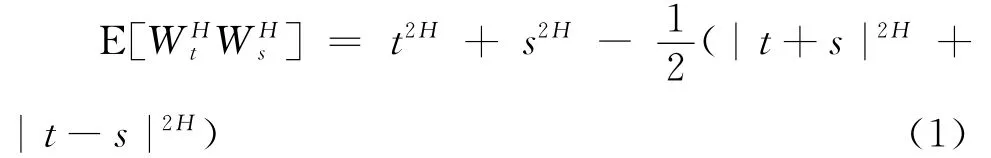
2.1 模型假设

（1）无风险利率r为常数且对冲投资组合的期望回报率等于无风险利率；

（2）投资策略每隔δt时间重新调整一次，这里

金融系统是一个自由度极大的复杂系统，大多数的投资者得不到充分的信息，并以一种非线性的方式对信息做出反应，即在信息达到一定临界值时才做出决策，这些噪声交易者会对前期忽略的信息做出“聚集、爆发”性的反应。同时噪声交易者大都具有“从众”心理，而理性投资者会利用“从众”噪声交易者的特征，并从中获利，这样进一步造成了市场的过渡波动，导致了市场波动的聚集性。而且，由于不同投资期限的投资者承担相同的风险水平，所以，不同期限尺度上的收益率具有类似的频率分布，即时间尺度上的不变性或称为自相似。所以，金融市场存在长记忆性，即过去的信息不仅影响当前，而且影响未来。本文采用次分数布朗运动来刻画备兑权证标的资产价格的变化过程，并考虑了现实中的交易费用，以期客观地反映权证市场的现实。

设赫斯特指数H∈（0，1），则次分数布朗运动是一个零均值的高斯过程W，使得W=0且协方差函数满足δt为有限固定且很小的时间间隔；

（3）交易费与交易额是成比例的。即买卖股票需要按股票价格支付比例交易费用c｜v｜S，其中c是每单位交易额应支付交易费，S是交易股票的价格，v＞0是买进，v＜0是卖出；

（4）备兑权证标的资产股票的变化过程在物理测度下满足：

其中：St表示股票的动态价格；μ表示股票的收益率；σ表示股票价格波动率；WHt表示赫斯特指数为H∈（1/2，1）的次分数布朗运动，且（2）式中的积分为关于高斯过程的Wick-Itô积分［21］。

在次分数Black-Scholes模型中，由于股票交易时会产生交易费用，从而完全复制使得交易总费用非常大，因此Black-Scholes中采用的无套利理论不再适用。本文采用Delta对冲策略对备兑权证的定价问题进行研究。

2.2 数理推导

现在考虑Wick-Itô型次分数Black-Scholes市场，该市场有两种投资产品，一种无风险资产即债券，另外一种有风险的标的资产如股票。其中无风险资产Pt，即债券价格变化过程满足如下方程：

其中r为无风险利率；风险资产价格变化过程满足方程（2）。

在风险中性和H∈（1/2，1）的假设条件下，我们利用Δ-对冲原理，推导出次分数布朗运动下带交易费用的备兑权证价格所满足的偏微分方程。

定理1 在风险中性世界里，备兑权证标的资产（股票）价格服从次分数布朗运动环境下，带交易费用的备兑权证的价格Vt在t（t∈［0，T］）时刻所满足的微分方程为：

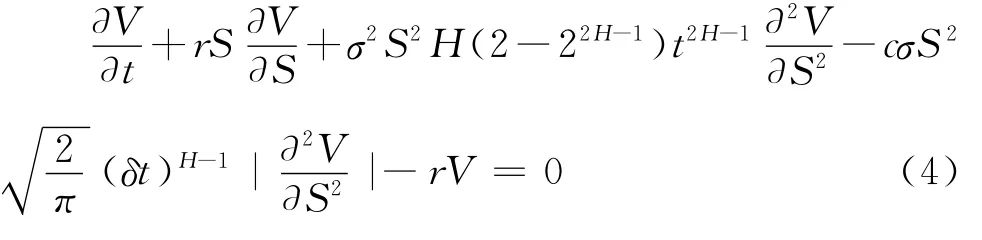
证明：考虑一个资产组合，包括一份衍生证券V（St，t）和Δ份股票St。则该资产组合在t时刻的价值∏t可以表示为∏t=Vt-ΔtSt。由于交易成本可以看作是投资者因买卖股票而产生的直接费用，因此在δt时间内，该证券组合持有者财富的变化过程可以表示为：选择恰当的证券组合可以消除δ∏t的随机性。令则（5）式可简化为：

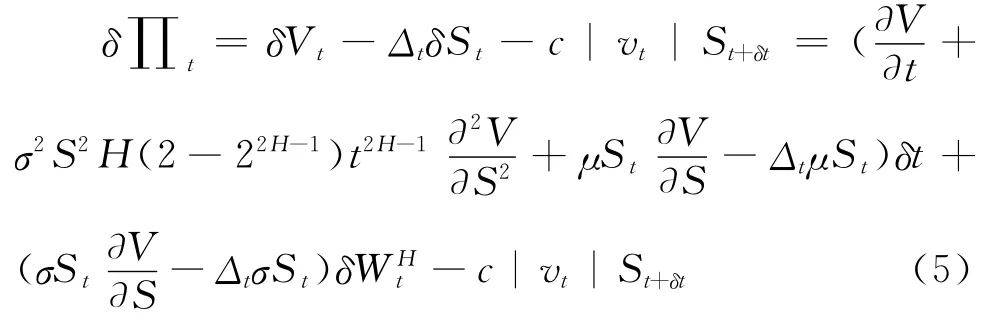
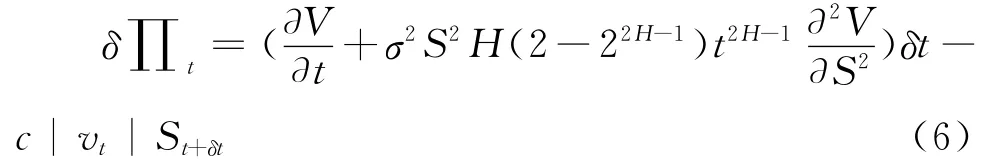
其中：

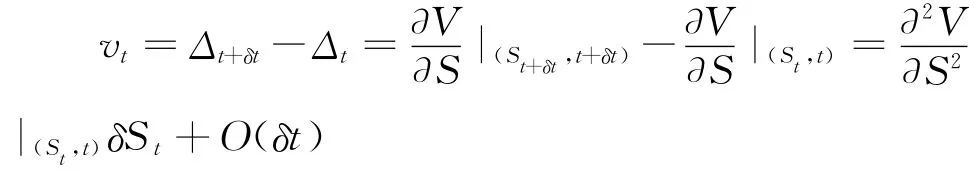
另一方面，根据式（2）易得δSt=St+δt-St= O（δt）+σStδWHt。同时利用，则有：

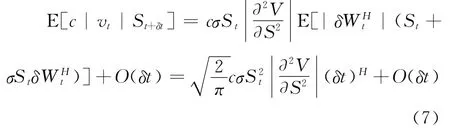
由假设条件4）可知E［δ∏t］=r∏tδt，再结合（6）和（7），并略去δt的高阶无穷小量，则有：

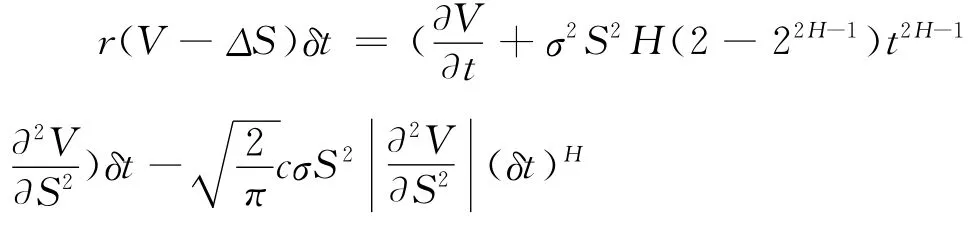
值得指出的是Γ=∂2V/∂S2，称为保值因子。对于备兑权证的多头而言，到期日的收益为凸函数，因此有Γ＞0，从而对于支付任意比例交易费的看涨或看跌备兑权证，由Black-Scholes公式得到的价值与本文模型得出的价格比较，差别仅在于波动率，即：

对于做空的备兑权证而言，到期日的收益为凹函数，故Γ＜0，类似地，两个模型所得价值的差别也在于波动率，即：

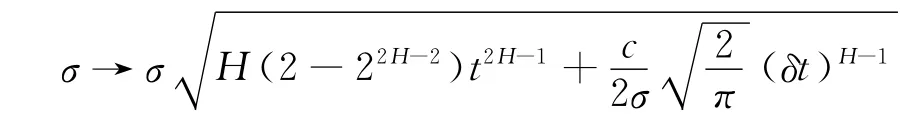
此外，在多头的情况下，为保证偏微分方程（4）的适定性，须保证：

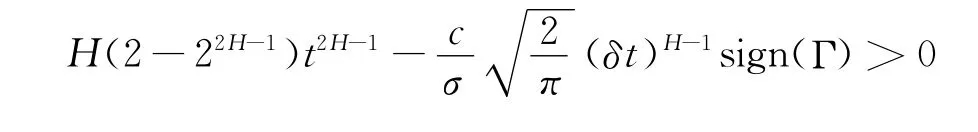
另一方面，由于（4）式中假设在δt相当短的时间内，备兑权证只发生一次头寸的变化，因此δt是一个常数，而且Hurst指数H对于一个确定的期权来是也是常数，从而（4）式与Black-Scholes微分方程有类似之处，这样启发我们用类似的方法求解。因此，在得到次分数布朗运动下备兑权证所满足的偏微分方程之后，利用变量替换，将偏微分方程化成Cauchy问题，再利用Poisson公式便可以得到次分数布朗运动下带交易费用的备兑权证定价公式。

定理2 到期日为T，执行价格为K，无风险利率r且股票价格波动率σ均为常数的备兑认购权证、在t刻的定价公式为：

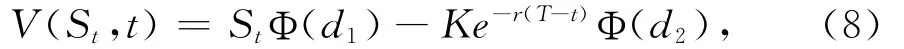
证明：请见附录。

3 参数估计

本文采用次分数布朗运动刻画备兑权证标的资产价格变化的行为模式，而如何有效估计随机微分方程（2）的参数是将定价模型应用于实践的关键。下面，我们在离散大样本条件下（观察间隔固定且观察次数足够多），对模型（2）进行参数估计研究。

采用Wick-Itô积分，可得随机微分方程（2）的解为：

从而对模型（9）进行参数估计实际上等价于对下面带漂移项的次分数布朗运动进行参数估计：

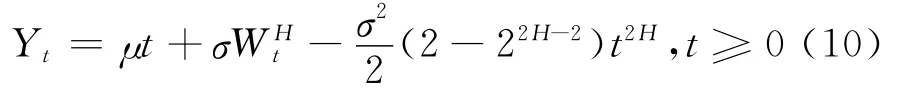
其中μ、σ和H为待估计的参数。

首先，假设观察间隔为h，从而得到N个观察量Y=（Yh，Y2h，…，YNh）t，这里t用来表示向量的转置。若用向量t=（h，2h，…，Nh）t表示观察点向量且t2H=（h2H，（2h）2H，…，（Nh）2H）t和WtH=（WhH，W2Hh，…，WNHh）t。显然，当1/2＜H＜1时，有E［Yt］∝t2H，即（Yh+Y2h+…+YNh）∝（Nh）2H。从而得到赫斯特指数的估计量可以表示为：

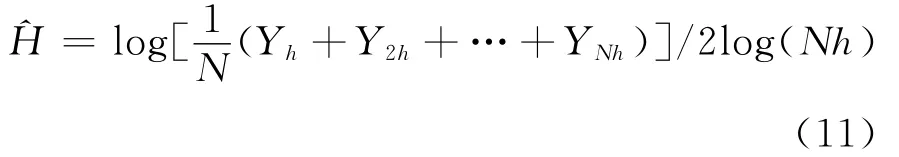
同时，由次分数布朗运动的性质知波动率σ可以估计如下：

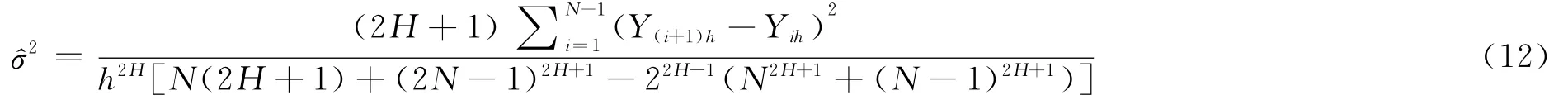
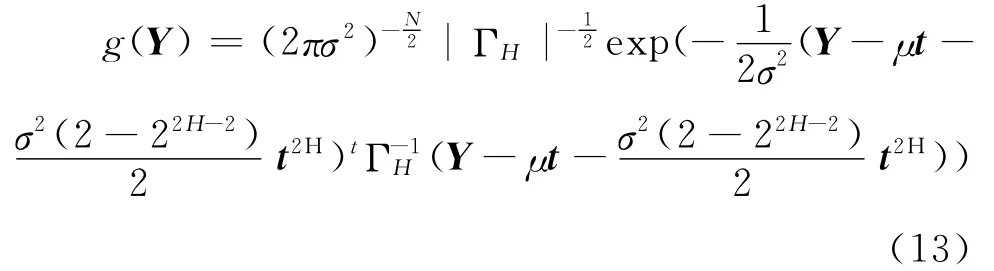
其次，注意到Yih服从正态分布，由多维正态分布的联合密度函数知Y的联合密度函数可以表示为：

其中：

对（13）式取对数并对μ求偏导，即得参数μ的极大似然估计量为：

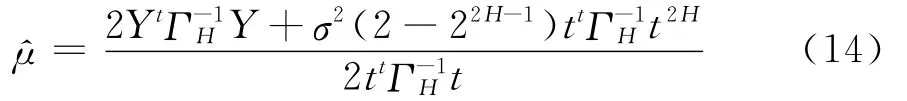
4 实证分析

为了评价定价模型的性能和解释本文模型的合理性，下面以我国权证市场的四只备兑认购权证为例进行实证分析（数据来源于国泰安数据库：http：//www.gtarsc.com）。在采用Black-Scholes模型计算备兑权证的价值时，采用Hull［22］介绍的标准差估计法求得各支股票的历史波动率。在采用分数布朗下期权定价模型［12］计算备兑权证的价值时，采用R/S方法估计赫斯特指数，并进一步采用二次变差方法估计波动率。在采用本文提出的带交易费用的备兑权证模型进行定价时，利用本文提出的（11）和（12）式对定价模型所需参数进行有效估计，所得的权证基本信息和求得的参数估计值如表1所示。

为了比较不同定价模型的定价误差程度，我们使用以下几个误差指标对定价模型的误差进行分析。令Pi和Qi分别表示模型的计算值和实际值，M为样本数，则有：

表1 四只备兑权证的定价参数值

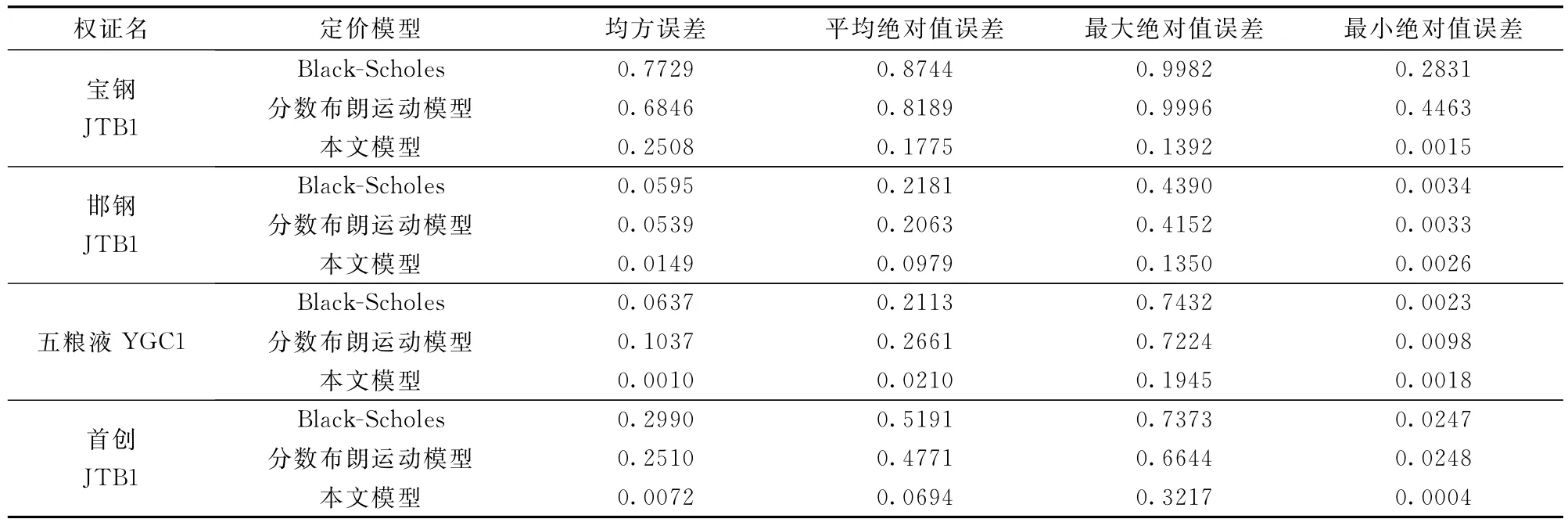
表2 定价模型的误差分析表

从而，利用权证市场的实际数据，采用不同定价模型计算不同剩余期限下备兑权证的价值，进一步求得以上四个指标值，所得结果如表2所示。从表中的各个误差结果可以看出，不管是均方差、平均绝对值误差，还是最小、最大绝对值误差，本文模型的定价结果都要优于Black-Scholes定价模型［1］和分数布朗运动定价模型［12］。这是由于Black-Scholes定价模型没有体现金融资产的长记忆性，而分数布朗运动定价模型没有体现交易费用的影响。因此，本文模型具有较好的定价效果，也说明了本文模型的稳健性。

4 结语

金融市场不仅存在长记忆性，而且投资者面临不可忽视的交易成本，考虑带交易成本的期权定价问题更加贴近实际市场模型。本文通过引入次分数布朗运动，运用证券组合原理得到了带交易费用的备兑权证定价模型。进一步采用我国权证市场的实际数据进行了实证检验，比较了Black-Scholes定价模型、分数布朗运动下定价模型以及本文定价模型的结果，实证结果说明了本文定价模型的准确性与合理性。而且在定价公式（8）中令H=1/2时，则本文定价公式与Leland［3］的定价公式是一致的，这表明了本文定价公式的普遍性，同时也说明了布朗运动只是次分数布朗运动的一个特例。

本文提出的次分数布朗运动下带交易费用的备兑权证定价模型既可以应用于研究标的资产具有长记忆性的期权定价问题，也可以应用于研究带交易费的期权定价问题。同时本文的研究思路和证明方法可以推广到研究一般高斯过程（如混合分数布朗运动、多尺度分数布朗运动、双分数布朗运动）下期权定价问题。

采用次分数布朗运动刻画金融资产的价格变化过程在一定程度上比以前模型有所改进，但是为简化模型而进行的众多假设显然与现实有出入，且模型中没有考虑到金融资产突发性跳跃、人的行为以及个人的风险偏好等因素。所以模型有待进一步改进和修正，采用新的柔性理论框架来定价期权迫在眉睫，比如国外有些学者将行为人的风险偏好因素引入到期权定价理论，为期权定价提供了新的方法途径，更适合解决实际资本市场中的金融问题。

附录

定理2的证明：

由定理1知备兑认购权证在t时刻的价值V（St，t）满足以下偏微分方程：

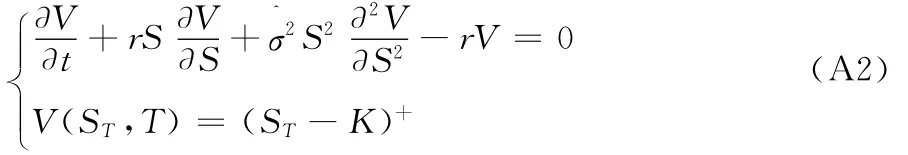
进一步，通过变量替换技术将求解（A2）式的问题就转化为求下面的Cauchy问题：

显然，方程（A3）的Cauchy问题的解可以用Poisson公式表示。从而有：（）∞2

对于I2，令y=，则-2τdy=dξ，从而有：

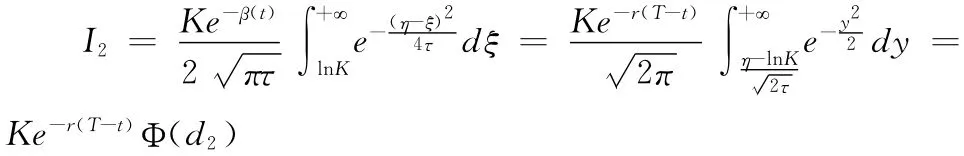
同理对于I1，令

而

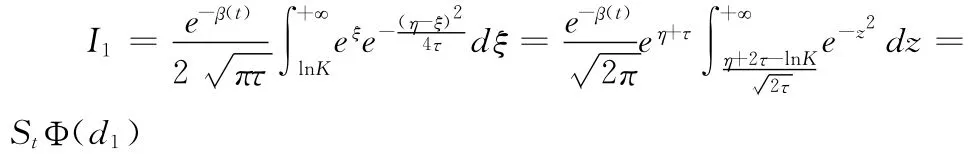
将I2和I2的值带入（A4）式即得（8）式成立。

［1］Black F，Scholes M.The pricing of options and corporate liabilities［J］.Journal of Political Economy，1973，81（3）：637-657.

［2］Merton R C.Theory of rational option pricing［J］.The Bell Journal of Economics and Management Science，1973，4（1）：141-183.

［3］Leland H E.Option pricing and replication with transaction costs［J］.Journal of Finance，1985，40（5）：1283-1301.

［4］Damgaard A.Computation of reservation prices of options with proportional transaction costs［J］.Journal of Economic Dynamics and Control，2006，30（3）：415-444.

［5］Tokarz K，Zastawniak T.American contingent claims under small proportional transaction costs［J］.Journal of Mathematical Economics，2006，43（1）：65-85.

［6］Peters E E.Fractal structure in the capital markets［J］. Financial analyst Journal，1989，7（32）：434-453.

［7］赵巍，何建敏.股票价格遵循分数Ornstein-Uhlenback过程的期权定价模型［J］.中国管理科学，2007，15（3）：1-5.

［8］刘善存，宋殿宇，金华.分数布朗运动下带违约风险的可转换债券定价［J］.中国管理科学，2011，19（6）：25-30.

［9］Necula C.Option pricing in a fractional brownian motion environment［R］.Working paper of the Academy of E-conomic Studies，Bucharest（Romania），2002.

［10］Xiao Weihin，Zhang Weiguo，Xu Weijun，et al.The valuation of equity warrants in a fractional Brownian environment［J］.Physica A，2012，391（4）：1742-1752.

［11］代军.权证定价中B-S模型与CSR模型的比较［J］.中国管理科学，2009，17（5）：20-26.

［12］吴鑫育，周海林，马超群，等.基于随机贴现因子方法的权证定价研究［J］.中国管理科学，2012，20（4）：1-7.

［13］Lin S J.Stochastic analysis of fractional Brownian motions［J］.Stochastics and Stochastics Reports，1995，55（1-2）：121-140.

［14］Duncan T E，Hu Yaozhong，Pasik-Duncan B.Stochastic calculus for fractional Brownian motion I.Theory［J］.SIAM Journal on Control and Optimization，2000，38（2）：582-612.

［15］Rogers L C G.Arbitrage with fractional Brownian motion［J］.Mathematical Finance，1997，7（1）：95-105.

［16］Björk T，Hult H.A note on Wick products and the fractional Black-Scholes model［J］.Finance and Stochastic，2005，9（2）：197-209.

［17］Tudor C.Some properties of the sub-fractional Brownian motion［J］.Stochastics，2007，79（5）：431-448.

［18］Tudor C.Inner product spaces of integrands associated to sub-fractional Brownian motion［J］.Statistics and Probability Letters，2008，78（14）：2201-2209.

［19］Tudor C.Sub-fractional Brownian motion as a model in finance［R］.Working Paper，Ann.Univ.Bucuresti，Mathematica，2008.

［20］Yan Litan，Shen Gangjun，He Kun.It^o's formula for the sub-fractional Brownian motion［J］.Communication on Stochastic Analysis，2011，5（1）：135-159.

［21］Nualart D，Taqqu M S.Wick-Itôformula for regular processes and applications to the Black and Scholes formula［J］.Stochastics：An International Journal of Probability and Stochastic Processes，2008，80（5）：477-487.

［22］Hull J C.Options，futures，and other derivatives［M］.5th ed.New Jersey：Prentice Hall College Div，5th edition，2002.

Pricing Covered Warrants in a Sub-Fractional Brownian Motion with Transaction Costs

XIAO Wei-lin1，ZHANG Wei-guo2，XU Wei-jun2
（1.School of Management，Zhejiang University，Hangzhou 310058，China；2.School of Business Administration，South China University of Technology，Guangzhou 510640，China）

In order to reflect the long memory property of the financial asset，the sub-fractional Brownian motion is introduced to capture the underlying asset of covered warrants.The pricing model of covered warrants is proposed by using the theory of stochastic integration and the method of partial differential equations.Moreover，the problem of parameter estimation is also discussed in this paper.Finally，an empirical study based on China's warrant market is presented.The pricing results of different models illustrate that the long memory property and the transaction costs have a significant impact on pricing results.

sub-fractional Brownian motion；transaction costs；covered warrants；partial differential equation；quadratic variation

F830.59

：A

1003-207（2014）05-0001-07

2012-03-14；

2013-11-06

国家社会科学基金重大招标项目（11&ZD156）；国家杰出青年科学基金资助项目（70825005）；国家自然基金资助项目（71101056，71171086）

肖炜麟（1981-），男（汉族），湖南衡南人，浙江大学管理学院，副教授，研究方向：资产定价与数量金融.