寿险定价的线性优化模型

王 波

（浙江广播电视大学工商学院，浙江宁波 315016）

寿险定价的线性优化模型

王 波

（浙江广播电视大学工商学院，浙江宁波 315016）

实际的金融市场中存在多种不同期限的利率。在定义最大累积函数的基础上建立了一个称为“收支问题”的线性规划模型，这个模型的最优值刻画了合理安排保费资金的投资期限所能够达到的最大保险支付水平，从而给出了多利率条件下寿险费率的计算依据。使用局部优化方法证明了收支问题最优解的两个性质，这些性质说明在满足保险支出的条件下，保险收入资金应该优先考虑期限较长（即利率较大）的投资。对于典型的寿险产品模型，给出了最优解的结构，针对两个具体实例列出了计算结果。结果表明，在保险费率的计算中，起主要作用的是最大期限的利率，其次是不同利率的一个综合水平。

多种利率；最大累积函数；线性优化；收支问题；寿险定价

1 引言

传统的精算理论是按照单一的预定利率计算寿险费率的，但是一般情况下实际的金融市场利率与预定利率并不一致，因此产品的定价要受到市场利率的影响。这个影响来自于两个方面，一个是利率随机性所带来的风险，另一个是利率的期限结构。关于前者，自1971年以来，一批学者对随机利率下的寿险定价进行了系统的研究。随机的利率模型主要有两种，早期采用时间序列方法对息力函数进行建模，自1990年以来部分学者采用摄动方法，利用O-U过程，Wiener过程和反射Wiener过程对息力累积函数进行建模，基于这种模型Beekman和Fuelling［1-2］，De Scheppe等［3-4］，Perry和Stadje［5］，Milvesky［6］研究了确定年金在随机利率下的现值，得到了期望值和方差的一些公式以及矩母函数和分布函数；Kaas等［7］，De Schepper等［8］相继利用凸序的相关性质给出了随机利率下年金现值的上界。此外Parker［9］还讨论了随机利率下贴现函数的问题，Zaks［10］则在假定各年利率均为独立且具有相同期望和方差的随机变量序列下，求出了确定年金累计值的期望和方差公式。

尽管随机利率下的寿险精算取得了比较丰富的成果，但是要应用于实际却有很大的难度。一般情况下寿险保单并不使用随机模型进行定价，这是由于随机模型虽然能在一定程度上降低利率的不确定性，但是并不能消除利率不确定性所带来的风险；同时寿险具有长期性的特点，而现实的金融市场复杂多变，我们很难对长时间内的利率建立合理的模型并作出准确的预测与估计，因此寿险业更愿意采用确定性的定价模型。同时为了规避利率风险，通常是采用一个比较保守的预定利率加上分红的方法。

与随机利率下的大量研究相比，关于利率期限结构的影响在文献中却很少涉及，当市场利率水平较高的时候，这种影响并不明显。以中国为例，从上世纪八十年代末到九十年代中期一直处于高利率的环境之中，其中一年期的存款基准利率最高的时候曾经达到11.34%，在大部分的时间内都高于当时寿险业8.8%的预定利率，所以当寿险准备金采用一年期利率投资生息时，并不会影响未来的保险偿付能力，这时候就不会去关注利率期限结构的影响。但是自从1996年以来，由于宏观经济形势发生了很大的变化，人民银行持续地下调基准利率，一年期存款利率最低的时候达到了1.98%，导致保险监管部门将预定利率调低到了2.5%。由于新的预定利率与原来8.8%的水平有较大的差距，所以一度对寿险业务的发展产生了较大的影响，同时当一年期利率低于预定利率时，寿险公司原有的资金运用方法有可能会产生巨大的利差损失。考虑到一般情况下长期的利率要高于一年期的短期利率，因此就提出了一个问题：我们是否可以通过对寿险资金的投资期限进行合理安排以提高保险金的支付能力，或者说提高寿险公司的盈利能力？最大能够达到多少？

基于上述背景，王波［11-12］提出了在多利率条件下合理配置保费资金的投资期限以求得最大的保险金额，田存福等［13］则考虑通过优化责任准备金的投资期限以求得最大的期末盈余。两者都是利用线性规划建立模型，区别主要是目标函数不同。由于上述模型都是根据每个时间点资金的流入与流出相等的原则构造线性规划的约束，不便于对优化解的性质作进一步的分析，因此本文在定义最大累积函数的基础上根据收支相等原则建立了一个称之为“收支问题”的线性规划模型。根据这个模型我们能够计算出多利率条件下最大的保险金支付水平，从而给出费率定价的依据，同时使用局部优化方法证明了最优解的两个性质，由此给出了典型寿险产品收支问题的优化解结构。这不仅简化了实际应用中的计算，而且还基本上回答了这么一个问题：在寿险精算中，起主要作用的是什么样期限的利率？这既为预定利率的制定确立了理论基础，又为寿险资金的运用提供了参考意见。

2 最大累积函数

假设市场上有T种无风险利率，期限分别为1，2，…，T，对应的利率为it≥0（复利），其中t表示利率期限。我们将1个单位的资金在经过总期限为t的数次投资计息后所得到的最大本利和用函数v（t）来表示，即：

v（t）是利息理论中累积函数概念［14］在多利率条件下的一个推广，我们称之为最大累积函数（maximum accumulation function），特别地规定v（0）=1。一般情况下，长期利率要高于短期利率，这时候就有v（t）=（1+it）t（1≤t≤T）。

根据定义，v（t）满足超指数性质，即对于任意的t1和t2，有v（t1）v（t2）≤v（t1+t2）。如果对于任意的1≤t1，t2≤T≤t1+t2，函数v（t）还满足条件：

那么当t＞T时，我们就有v（t）=v（T）·v（t-T），这时v（t）称为T周期的。

条件（1）意味当投资期限t大于T时，其最优投资方案的唯一性，即首先考虑期限为T的投资，然后再考虑剩余期限内的投资。如果更进一步地假设，对于任意的1≤t1，t2≤t≤t1+t2≤T，最大累积函数v（t）均满足条件：

那么我们就称v（t）为正规的。

3 收支问题

这节中我们考虑一种简化的寿险定价模型。在模型中，保险费的收入期是从时间1到T（即最大利率期限），时间x的期望收入为f（x）（x=1，2，…，T）；保险金的支付期是从时间T+1到2T，当保险金额等于1个单位时，时间x的期望支出为g（x）（x=T+1，T+2，…，2T）。我们的问题是：如何来安排保险费的投资期限，使得将来能够支付的保险金达到最大？也就是下列线性规划问题：

其中v（t）是最大累积函数。我们称上述规划问题为收支问题（income-outcome problem，IOP），f（x）和g（x）分别称为IOP的收入函数和支出函数。

命题1如果最大累积函数v（t）是T周期的，则IOP存在最优解，对于每一个min（f（i），^λg（T+i）/v（T））。

显然^x′满足约束条件（3），（4）和（5）（s≠T+ i），且有：-v（k-i）v（T+i-j）/v（k-j））

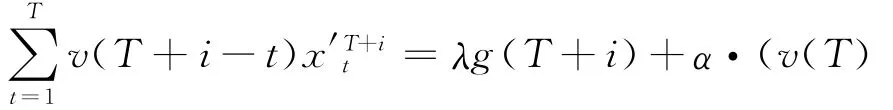
由于v（t）是T周期的，根据式（1），有：

v（k-i）v（T+i-j）≤v（T+k-j）=v（T）v（k -j）

如果v（k-i）v（T+i-j）＜v（T）v（k-j），则i），这样就得到了一个新的最优解（^x′，^λ），在这个最优解中。因此可以断言存在最优解（^x，^λ），使得）。由于上述过程中并不改变其它基变量的数值，所以使用相同的方法，最终就能够得到一个最优解，使得对于每一个i，，证毕。

命题1表明了，IOP的最优解中时间i的保险收入优先支付时间T+i的保险金支出，那么多余的收入是如何支付不足的支出？下面先来考虑一种特殊的情况。

对于一个IOP，如果存在1≤μ＜T，使得下面两种情况之一成立：

（1）当x≤μ时f（x）=0；x≥T+μ+1时g（x）=0。

（2）当x≥μ+1时f（x）=0；T+1≤x≤T +μ时g（x）=0。

那么我们称该IOP为半收支问题（quasi income-outcome problem，QIOP）。

命题2假设最大累积函数v（t）是正规的，则QIOP存在最优解，对于它的任意两个基变量＞0和＞0，如果i≤j，则有k≥l。

证明：与命题1类似，利用式（2），略。

如果最大累积函数是正规的，命题2显示QIOP的最优解具有非常良好的结构：最近时刻的收入优先支付最远时刻的支出。例如图1所示，时间μ+1的收入首先支付时间T+μ的支出，如果有盈余，则支付时间T+μ-1的支出，如果有亏缺，则亏缺部分由时间μ+2的收入来支出；最后时间T的收入支付T+1时刻的支出，如果有盈余，则支付T+2时刻的支出，如果有亏缺，则亏缺部分由T-1时刻的收入来支出。准确地说，最优解的基变量是｛，j=1，2，…，T；μ+1=t1≤t2≤…≤tT=T；T+μ=s1≥s2≥…≥sT=T+1｝，tj取遍从μ+是最优解矛盾。所以v（k-i）v（T+i-j）=v（T）·v（kj），由此可以推出1到T的每一个值，sj取遍从T+1到T+μ的每一个值。

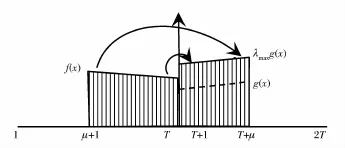
图1 QIOP最优解示意图（第一种情况）

根据命题1与2，当f（x）与g（x）满足一定的条件时，我们能够清楚地描述IOP最优解的结构，即下列推论：

推论1 假设最大累积函数v（t）是正规的，则IOP存在最优解i）/v（T））；i=1，2，…，T｝是的基变量，并且有：

（1）如果存在正整数μ≤T，使得x≤μ时h（x）≤0，μ＜x≤T时h（x）≥0，其中h（x）= f（x）-（T+x）/v（T）。则^x的其它基变量为｛，j=1，2，…，T；μ+1=t1≤t2≤…≤tT=T；T+μ=s1≥s2≥…≥sT=T+1｝，tj取遍从μ+ 1到T的每一个值，sj取遍从T+1到T+μ的每一个值（图2）；

（2）如果存在正整数μ≤T，使得x≤μ时h（x）≥0，μ＜x≤T时h（x）≤0（h（x）同上）。则^x的其它基变量为｛，j=1，2，…，T；1=t1≤t2≤…≤tT=μ；2T=s1≥s2≥…≥sT=T+μ+ 1）｝，tj取遍从1到μ中的每一个值，sj取遍从T+μ +1到2T的每一个值（图3）。

图2 IOP最优解示意图（一）

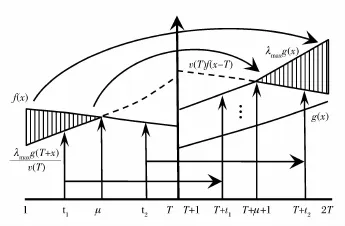
图3 IOP最优解示意图（二）

对于满足推论1条件的IOP，最优解的结构可以这样来描述：i时刻的收入优先支付T+i时刻的支出，最近时刻多余的收入优先支付最远时刻不足的支出。因而我们可以利用二分搜索法来计算最优值而无需求解线性规划问题。图2和图3还定性地给出了最优解中不同期限利率的作用大小，如果阴影部分面积较小，那么最大期限以外的其它利率的作用就不大；相反阴影部分面积越大，那么其它利率的作用也就越大。虽然在实际的金融利率市场中，最大累积函数v（t）不一定是正规的，甚至还不一定是T周期的，但是只要长期利率高于短期利率，我们就可以把推论1中所给出的结构作为（近似）最优解，这样所计算出的最大保险金额要小于理论上的最大值，因而从定价上来说是安全的。

4 多利率下的寿险定价

现在我们来考虑一般情况下的寿险定价模型。假设有一大群相同的保单，时刻1表示保单签发的时间，ω为保单的终止时间。保险人在时间x（x= 1，2，…，ω）的期望保险费收入为P（x），当保险金额等于一个单位时，保险人按照保险合同在时间x所要支付的期望保险金为R（x）。为简单起见，在本文中不考虑附加保险费用。按照收支相等的原则，可以假设保险支出的资金全部来源于保费的收入及其投资利息，与IOP相似，我们考虑下列线性规划问题：

其中，v（t）是最大累积函数。在本节中我们均规定v（T+t）=v（T）·v（t）。变量表示在时间t的保险收入中将用于支付时间s的保险金支出的数量，由于时间t收入的资金数在s时刻所能得到的最大本利和是v（s-t），所以上述问题准确地刻画了通过合理配置保险收入（由P（t）表示））的投资期限（由表示）能够使保险金支出水平（用λR（s）表示）达到最大，我们称之为广义收支问题（generalized income-outcome problem，GIOP）。而这个线性规划问题的最优值，则给出了多利率条件下保险费率的计算依据。要说明的是，在第二个约束式中我们使用了等式条件，而不是≥条件。这是因为在实际应用中，GIOP的可行解一般都是存在的，也就是说，所有的保费收入在投资生息后都能够用在将来的保险金支出上。

在我们的定义中，P（x）与被保险人缴纳保费的方式有关，R（x）与寿险产品的设计有关。当这两个函数确定后，影响精算定价的就是最大累积函数v（t）。由于对于任何的t≥0，v（t）=vi（T）· v（t-iT）（iT≤t≤（i+1）T），因此我们考虑对GIOP进行简化。不失一般性，假设ω=kT（k≥1），令：

命题3如果保险支出发生在保险收入之后，那么GIOP与对应的IOP等价。

证明：不妨假设保险收入发生在时间1至lT之间，保险支出发生在时间l T+1至kT之间。如果是相应IOP的一个可行解，对于每一个分量，我们按照下式构造GIOP的一组分量：

命题4如果在保险期（ω=k T）内P（x）单调减少，R（x）单调增加，那么GIOP与对应IOP的最优值是相等的。

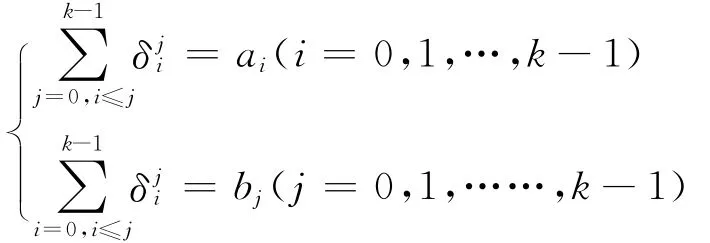
对于每一个基变量^x′s′t′，我们按照下式构造GIOP的一组分量：

命题3和4表明了在多利率条件下，包括生存年金、定期人寿保险乃至更为广泛的一类寿险产品，其定价模型GIOP可以归结为相应的IOP。由于在P～（x）和R～（x）的定义中唯一起作用的是期限为T的利率，这个结果也就意味着如果保险期比最大利率期限大的话，那么在精算定价中起主要作用的就是最大期限的利率iT，也就是最大利率。

最后我们来看一种特殊情况，当保险期与最大利率期限相等时，那么有（x）=P（x），（x）= v（T）·R（x-T）。根据命题1，相应的IOP存在最优解（x，），其中=min（（i），（T+ i）/v（T））=min（P（i），^λR（i））是基变量，即GIOP存在基变量为=min（P（i），R（i））的最优解，这可以解释为在最优解中保险费收入优先支付同一时间的保险金支出。如果P（x）/R（x）变化不大的话，那么绝大部分的保费收入将用于支付同一时间的保险金支出，此时费率的计算与利率的大小基本无关；相反如果P（x）/R（x）变化较大的话，那么不同期限的利率（不含最大期限的利率iT）均起到一定的作用。

5 应用分析

在本节中我们将给出两个具体实例的计算结果，其中生命表均参照美国1979—1981全体人口生命表。假设最大利率期限为5年（T=5），其利率（复利）分别如下表所示：

表1 假设的利率期限结构表

我们发现对应的最大累积函数v（t）不是正规的，甚至还不是T周期的（因为v（5）·v（3）＜v2（4）），所以我们根据推论1中的最优解结构使用二分搜索法所计算出的最大保险金额要略微小于理论上的最大值。

第一个例子是终身生存年金，保费缴付方式是年缴（等额），年金支付形式是每年领取（等额），并且有十年固定年金。

设年龄为a岁者la（生命表中年龄为a的生存人数，下同）人，每人都投保上述终身生存年金，年缴保险费为P0（从a岁至a+n-1岁），共缴付n年。如果用时间1表示第一次缴费的时间（a岁），那么在a+n岁时生存者la+n人在时间x所缴付的保险费为P（x）=P0la+n（1≤x≤n）。由于n一般不是T的倍数，所以我们将初始时间前移n0，其中n0= T-n%T，n%T是n除以T的余数，那么在缴费期间P（x）则为如下的等价形式：

从a+n岁开始，生存者每年领取生存年金（具有十年固定年金），那么当年金金额为1个单位时期望的年金支出为：

上式中ω表示的是生命表中的极限年龄。

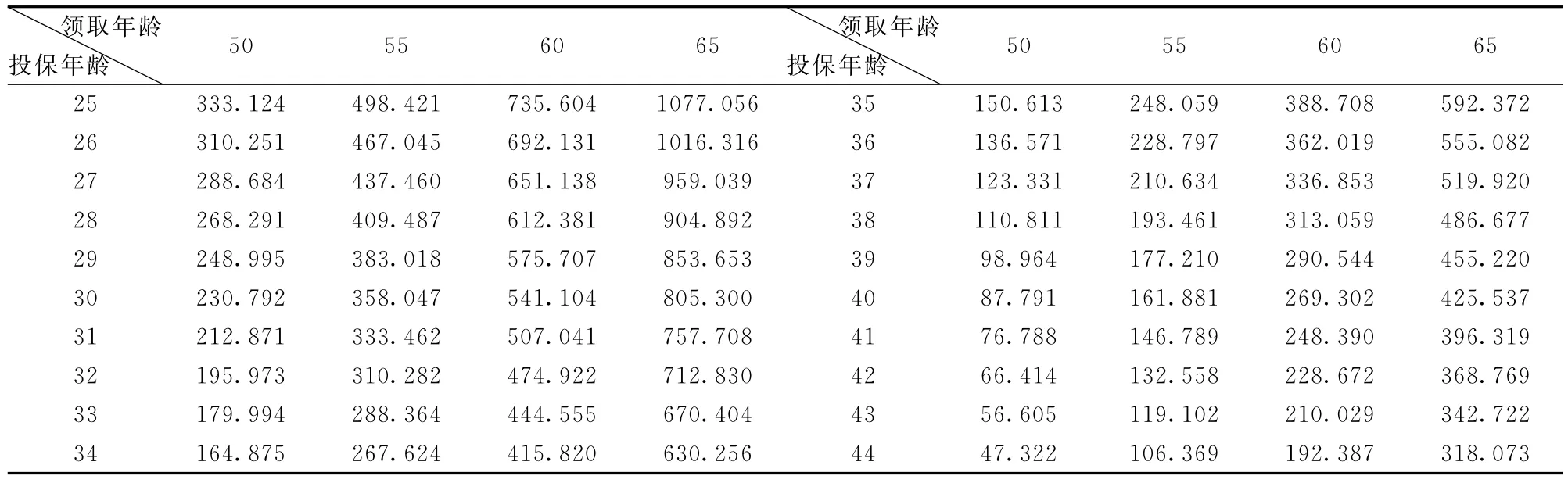
表2 最大年金表

表3 最大保险金额表

通过计算我们发现表中数值基本上与以最大期限的利率（本例中是5%）作为单一预定利率所计算出来的相同。原因是保险期比较长，同时（x）/（T+x）（1≤x≤T）变化不大，接近于一个常数c，由命题1，其对应的IOP的最优值^λ近似地等于c·v（T）。因此在生存年金的费率计算中，最大期限的利率起到了主要的作用，也就是说，资金的运用应该以利率最高的长期投资为主。

第二个例子是定期人寿保险，保费缴付方式也是年缴（等额），保险金即刻赔付。为了简单起见，我们假设保险期n是T的倍数，保险资金在一年之内是不计利息的（即最小计息期限是一年）。

设年龄为a岁者la人，每人都投保n年期人寿保险，每年年初缴付保险费为P0，那么在时间x的期望保险费收入为：

当保险金额为1个单位时，期望的保险金支出则为：

由于生命表中死亡人数基本上是随着年龄增大而增加的，同时保险期是T的倍数，所以R（x）和（x）接近于单调增加函数，而P（x）和（x）均为单调减少函数。根据命题4，相应GIOP与对应的IOP的最优值可以认为是相等的，我们称之为最大保险金额，并且也基本满足推论1中的条件（第2种情况）。表3是利用二分搜索法计算的年缴纯保费1个单位时的最大保险金额表。

6 结语

在本文中，我们应用线性优化的方法解决了在多利率条件下寿险费率的定价问题。命题1和2表明了这么一个事实，如果长期利率高于短期利率，那么保险收入资金的运用在满足保险支出的情况下应该优先考虑期限较大（也就是利率较大）的投资，因而在保险费率的计算中，起主要作用的是最大期限的利率，其次是不同利率的一个综合水平。这个结果也就意味着，在寿险资金的运用中，应该考虑以长期投资为主，这为预定利率的确立提供了可靠的理论基础。如果将收支问题中的收入函数看作为“本金”，将最优值与支出函数的乘积看作为“累积值”，那么实际上我们已经把单一利率下的现值与终值的概念推广到了多利率的情况。在这种情况下，“本金”、“现值”或者“终值”不再是某一个时刻的金额数值，而是一个时间区间（长度为最大利率期限T）上的收入或者支出金额的分布，这为推广传统的单一利率下的利息理论，建立更广泛意义的利率期限结构框架下的利息理论提供了模型基础。

附录

1.命题2的证明

命题2假设最大累积函数v（t）是正规的，则QIOP存在最优解，对于它的任意两个基变量＞0和＞0，如果i≤j，则有k≥l。

证明：这里我们只证明QIOP的第一种情况，第二种情况与此类似。如果QIOP的最优解中存在两个基变量＞0，＞0，其中μ+1≤i≤j≤T，T+1≤k＜l≤T+μ。令，构造一个新的解：

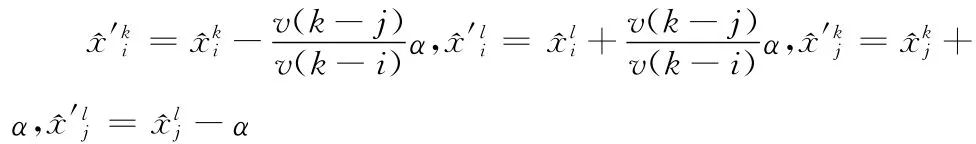
因为μ+1≤i≤j≤T＜k＜l≤T+μ，所以有1≤l-j，k-i≤l-i＜T。由于v（t）是正规的，根据式（2），有v（l，即。如果，与是最优解矛盾。所以有，则，由此可以推出，即得到了一个新的最优解，在这个最优解中不同时存在两个基变量。由于除了以外，其它的基变量均没有改变，所以使用相同的方法，最终就能够得到一个最优解，在这个最优解中不会同时存在两个基变量≤T＜k＜l），证毕。

2.下面是第3节系推论1中两种典型情况的最大保险金额λmax的类C语言二分搜索算法，其中ε是给定的表示误差范围的一个小数，λh是给定的保险金额较大的初始值，数组变量Sp和Ls分别表示多余的保险收入和不足的保险支出。

（1）f（x）单调增加（含常值），g（x）单调减少（图2）。

（2）f（x）单调减少，g（x）单调增加（图3）。

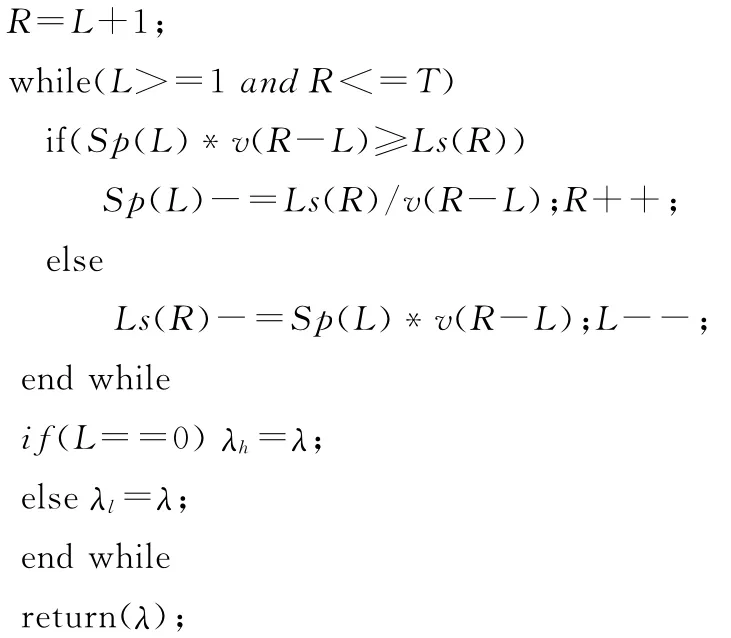
3.第5节实例中对应IOP的收入函数~P（x）和支出函数~R（x）的表达式。

（1）终身生存年金

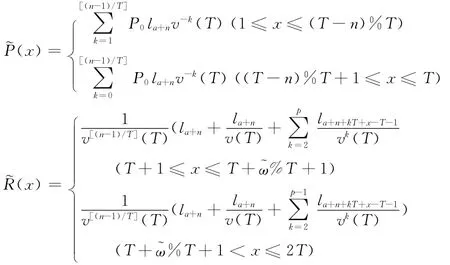
（2）定期人寿保险

其中a是投保年龄，n=pT（p≥1）。

［1］Beekman J A，Fuelling C P.Interest and mortality randomness in some annuities［J］.Insurance：Mathematics and Economics，1990，9（2-3）：185-196.

［2］Beekman J A，Fuelling C P.Extra randomness in certain annuity models［J］.Insurance：Mathematics and Economics，1992，10（4）：275-287.

［3］De Schepper A，De Vylder F，Goovaerts M，et al.Interest randomness in annuities certain［J］.Insurance：Mathematics and Economics，1992，11（4）：271-281.

［4］De Schepper A，Goovaerts M.Some further results on annuities certain with random interest［J］.Insurance：Mathematics and Economics，1992，11（4）：283-290.

［5］Perry D，Stadje W.Function space integration for annuities［J］.Insurance：Mathematics and Economics，2001，29（1）：73-82.

［6］Milevsky M A.The present value of a stochastic perpetuity and the Gamma distribution［J］.Insurance：Mathematics and Ecomomics，1997，20（3）：243-250.

［7］Kaas R，Dhaene J，Goovaerts M J.Upper and lower bounds for sums of random variables［J］.Insurance：Mathematics and Economics，2000，27（2）：151-168.

［8］De Schepper A，Goovaerts M J，Dhaene J，et al. Bounds for present value functions with stochastic interest rates and stochastic volatility［J］.Insurance：Mathematics and Ecomomics，2002，31（1）：87-103.

［9］Parker G.Two stochastic approaches for discounting actuarial function［J］.Astin Bulletin，1994，24（2）：167-181.

［10］Zaks A.Annuities under random rates of Interest［J］. Insurance：Mathematics and Economics，2001，28（1），1 -11.

［11］王波.多种利率条件下寿险费率的测算［J］.上海，上海保险，2002，197（3）：17，28.

［12］王波.线性规划在寿险精算中的应用［J］.北京，数学的实践与认识，2006，36（11）：48-53.

［13］田存福，刘芳，吴黎军.责任准备金的最优投资计划［J］.北京，系统工程理论与实践，2005，25（6）：76-86.

［14］Kellison G S.The Theory of Interest［M］.3th ed.New

York：Irwin/McGraw-Hill，2009.

Linear Optimization Model for Life Insurance Pricing

WANG Bo
（Institute of Business of Zhejiang Radio and TV University，Ningbo 315016，China）

There are various interest rates of different terms in the actual financial markets.In order to calculate the life insurance rates under the condition of multiple interest rates，a linear programming model which is called“Income-outcome problem（IOP）”was established on the basis of the definition of maximum accumulation function，and its optimal value describes the maximum level of insurance payment that can be achieved through the rational arrangement of investment term of premium funds.Using local optimizationmethod，two properties of the optimal solution of IOP are proved，and these properties show that the premium income fund should gives priority to the investment which has longer term（that is，larger interest rates）on the condition of meeting the insurance expenditures.For some typical life insurance product model，we give the structure of the optimal solution and list the calculated results of premium rate of two specific examples.The results show that the main factor in the calculation of premium rates is the longest term interest rate，followed by an comprehensive level of the different interest rates.The model of this paper also provides the basis for creating generalized theory of interest under the condition of multiple interest rates.

multiple interest rates；maximum accumulation function；linear optimization；income-outcome problem；life insurance pricing

F840

：A

1003-207（2014）05-0033-09

2012-04-29；

2013-05-09

王波（1970-），男（汉族），浙江宁波人，浙江广播电视大学工商学院，讲师，研究方向：最优化算法与应用.